预应力平行钢丝束高温力学性能
2020-03-12肖丽萍李国强汪贤聪
杜 咏, 肖丽萍, 李国强, 汪贤聪
(1.南京工业大学 土木工程学院, 江苏 南京 211816;2.同济大学 土木工程防灾国家重点实验室, 上海 200092)
预应力张拉钢结构广泛应用于大跨度结构体系,如索网结构、张弦梁和悬索桥等,其中的预应力钢索是其关键部件[1].然而,预应力钢索在火灾中会受到不同程度的损伤,其火灾安全性受到科研及工程人员越来越多的关注.在预应力张拉索体分类中,预应力平行钢丝束在现役预应力钢结构中有较广泛应用[2],因此,准确测定预应力平行钢丝束高温力学性能指标,可为研究预应力张拉钢结构在火灾场景中的力学响应提供重要的材料高温性能参数.
目前,对于预应力混凝土用钢丝和钢丝束已建立了较系统的常温力学性能指标[3-8].Wang等[9]研究表明,在各温度水平下,平行钢丝束的断裂状态与单根钢丝基本一致,但前者的高温力学性能指标比后者退化更为严重.Xiong等[10]研究表明,稳态试验方法适用于测量高强钢的高温力学性能指标.周浩[11]研究表明,只有当钢索体遭遇高于600℃高温时,热蠕变效应才能显著表现出来,而此时其极限强度不足常温下的10%.
钢丝束表面几何形状不规则,若采用接触式高温应变测试方法,位移计夹持端在拉伸过程中会不可避免地产生相对滑移,导致试验误差;且因仪器量程的限制,只能测量材料极限强度之前的应力-应变曲线段.Chu等[12]提出了非接触式应变视频测量(CCDC)系统的应用原理;Lyons等[13]的高温材性试验表明了CCDC技术的可行性和准确性;Du等[14]开展了非接触式测试技术与传统接触式测试手段的对比性试验.上述研究均表明CCDC系统不仅精度可靠,且适用于测试表面形状复杂的试件.
鉴于此,本文采用CCDC系统,基于稳态试验方法,将平行钢丝束试件升温至目标温度且温度恒定后,对其进行单向拉伸直至断裂,以研究平行钢丝束高温下的应力-应变全过程.
1 试验
1.1 装置
CCDC系统如图1所示.由图1可见,加载设备为Instron1334液压伺服万能材性试验机,采用其配套的SF-16管状高温炉对试件加温,炉膛净尺寸为30.0cm×10.5cm(高×直径),最高温度可至 1250℃,高温炉内配置上中下3片加热单元,以保证炉内温度均匀分布.
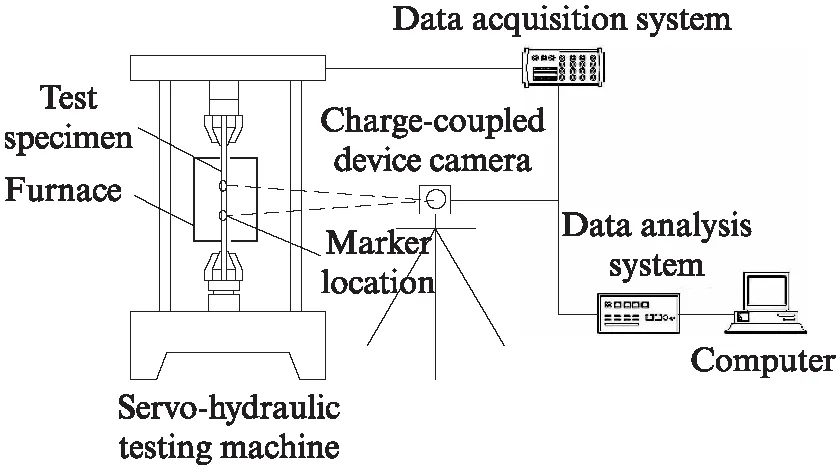
图1 非接触式应变视频测量系统Fig.1 CCDC system
1.2 试件
图2为抗拉强度1670MPa的7根×7mm高温单向拉伸平行钢丝束试件.在平行钢丝束试件测试区均匀喷涂黑白相间的散斑带(见图3).通过CCD摄像机记录试件变形过程中材料表面的散斑图变化情况,将其以灰度矩阵的形式存储在计算机中,测试系统分析软件实时输出试件标距段(本试验选取标距不大于1.5cm)位移及应变随温度的变化历程.
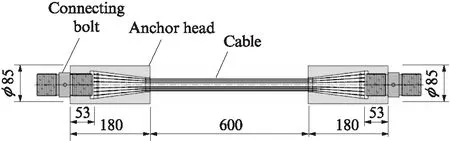
图2 高温单向拉伸平行钢丝束试件尺寸Fig.2 Size of parallel wire cable specimen at elevated temperature(size:mm)

图3 平行钢丝束表面高温喷涂标记Fig.3 High temperature paint markers on a cable surface
1.3 试验过程
在试件升温前,用双头螺纹连接螺栓将试件上锚杯端与试验机连接,保持试件下锚杯端为松弛状态,以消除热膨胀对试件的影响;当试件温度升至目标温度并完成恒温保持后,再进行单向拉伸试验.
在稳态试验中,将炉内温度从室温(20℃)升至100、200、300、350、400、450、500、550、600、700、 800℃,升温速率为10℃/min[15],并在各温度水平下恒温20~30min,以保证钢索截面温度分布均匀.以 0.05mm/s 的拉伸速率对试件进行拉伸直至破坏,每1s收集5个数据,每个目标温度水平重复测试3个试件,试验值取其平均值.
1.4 试验现象
图4为各温度水平下平行钢丝束试件断口形貌.由图4可见:室温(20℃)下,试件断口位置在锚杯口附近,而其余温度水平下的试件断口位置均在受热区;在20~200℃时,试件断口形貌呈杯状,表现为脆性破坏,断口截面颜色呈黑色,钢丝表面仍具有金属光泽;随着温度的升高,在300℃时,试件断口形貌出现变化,部分钢丝沿着45°方向断裂,部分钢丝断口仍为杯状,试件仍以脆性破坏为主,断口截面颜色呈现黑黄色,钢丝表面原先的金属光泽开始变暗;在350℃时,大多数试件断口形貌呈锥形,表现为塑性破坏,断口截面颜色为深蓝色,钢丝表层出现脱落;在400~800℃时,随着温度的升高,试件中的钢丝颈缩现象越来越明显,试件断口形貌锥状化加剧,断口截面颜色变为黑灰色,钢丝表面逐步变为土黄色;当目标温度低于300℃时,试件破断时发出清脆声音,当目标温度高于400℃时,试件破断时仅发出微弱的“砰”声,在600~800℃时,试件断裂声尤为微弱.



图4 各温度水平下平行钢丝束试件的断口形貌Fig.4 Fracture morphologies of parallel wire cable specimens at different temperatures
2 试验结果分析
2.1 名义屈服强度
图5为高温下平行钢丝束试件的应力-应变(σ-ε)曲线指标示意图.由图5可见,在试件的σ-ε曲线上,与极限应变εpt,θ相对应的极限强度为fpt,θ,与比例极限应变εpp,θ相对应的比例极限为fpp,θ,与屈服应变εpy,θ相对应的屈服强度为fpy,θ,εpu,θ为试件断裂应变,Ep,θ为试件的弹性模量.其中θ表示温度.
表1为各温度水平下平行钢丝束试件名义屈服强度、极限应变和断裂应变试验结果,其中f0.20%-offset,θ、f0.50%,θ、f1.00%,θ、f1.20%,θ、f1.25%,θ、f1.50%,θ和f2.00%,θ分别为应变水平0.20%、0.50%、1.00%、1.20%、1.25%、1.50%和2.00%对应的名义屈服强度.由表1可见,与各应变水平相比,其2.00%应变水平下的名义屈服强度f2.00%,θ更接近极限强度fpt,θ,两者最大相差仅7.8%,故本文将f2.00%,θ作为平行钢丝束试件的高温名义屈服强度.
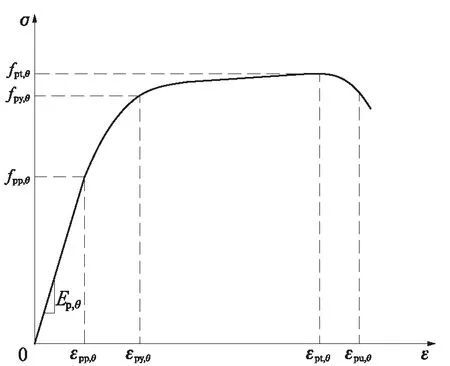
图5 高温下平行钢丝束试件的应力-应变曲线指标示意图Fig.5 Mathematical model for stress-strain relationships of parallel wire cable specimens at elevated temperature

表1 各温度水平下平行钢丝束试件名义屈服强度、极限应变和断裂应变试验结果
2.2 弹性模量
根据应力-应变关系曲线初始线性段斜率确定平行钢丝束试件的弹性模量Ep,θ;曲线线性段终点所对应的比例极限应变为εpp,θ,则比例极限fpp,θ=Ep,θ×εpp,θ.表2列出了各温度水平下平行钢丝束试件的弹性模量、比例极限及比例极限应变.

表2 各温度水平下平行钢丝束试件弹性模量、比例极限及比例极限应变
2.3 极限应变和断裂应变
图6为平行钢丝束试件极限应变(εpt,θ)、断裂应变(εpu,θ)试验值与文献[8]中建议值的比较.
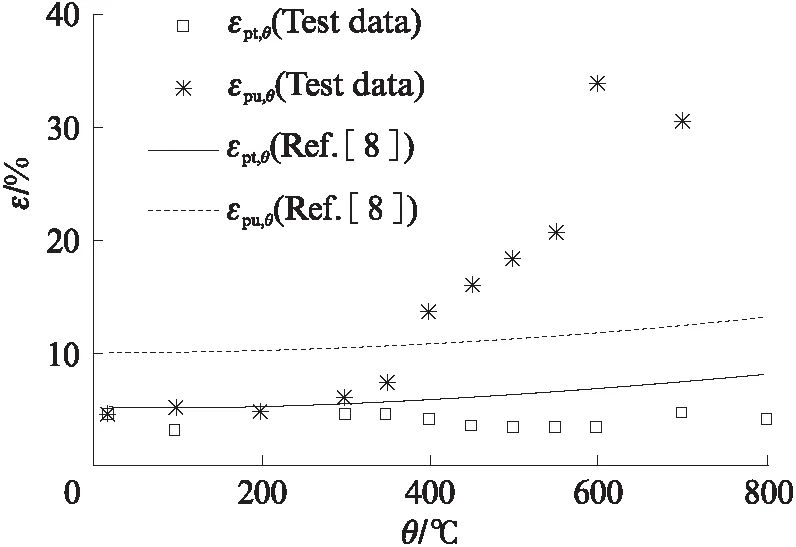
图6 平行钢丝束试件极限应变和断裂应变试验值与 文献[8]中建议值的比较Fig.6 Comparison of strain between test data and reference[8] of parallel wire cable specimens
由图6可见:在20~200℃时,平行钢丝束试件极限应变试验值与文献[8]建议值相差不大且随温度变化较小;高于200℃后,试件极限应变试验值呈下降趋势,而文献[8]建议值呈上升趋势;试件断裂应变试验值在300~400℃时接近文献[8]建议值;高于400℃后,试件断裂应变试验值呈显著上升趋势;文献[8]高估了平行钢丝束的极限应变,幅度达52.7%,低估了400℃后平行钢丝束的断裂应变,幅度达256.0%.
3 高温折减系数
3.1 力学性能指标高温折减系数
定义弹性模量高温折减系数kE,θ为高温下弹性模量Ep,θ与常温下弹性模量Ep的比值,即kE,θ=Ep,θ/Ep;极限强度高温折减系数kpt,θ为高温下极限强度fpt,θ与常温下极限强度fpt的比值,即kpt,θ=fpt,θ/fpt.
文献[8]推荐的预应力混凝土用钢索的高温名义屈服强度折减系数kpy,θ为各温度下2.00%应变屈服强度f2.00%,θ与90%极限强度fpt,θ的比值,即kpy,θ=f2.00%,θ/0.9fpt,θ,但20℃时试件的f2.00%,θ大于0.9fpt,θ(见表1),使得kpy,θ大于1,因此本文采用文献[16]建议的普通结构钢高温名义屈服强度折减系数计算公式——高温下名义屈服强度fpy,θ与常温下名义屈服强度fpy的比值,即kpy,θ=fpy,θ/fpy.
文献[8]中预应力混凝土用钢索的比例极限高温折减系数计算式kpp,θ=fpp,θ/0.9fpt,但本文的kpp,θ=fpp,θ/fpy值与文献[8]建议值更为接近,故本文按kpp,θ=fpp,θ/fpy来确定平行钢丝束比例极限高温折减系数.
3.2 屈服强度高温折减系数
图7为平行钢丝束试件名义屈服强度高温折减系数试验值与已有研究[8-9,17-18]的比较.由图7可见:(1)已有研究得出的预应力钢索名义屈服强度高温折减系数离散性较大;本文试验值与文献[8-9,17-18]给出的预应力钢索名义屈服强度高温折减系数较为接近,而与Xiong等[10]得出的高强钢名义屈服强度高温折减系数相差较大.(2)与汪贤聪[17]的钢绞线名义屈服强度高温折减系数相比,在低于 400℃ 时,由于平行钢丝束无缠绕效应影响,本文试验值略低于钢绞线试验值,当超过 400℃ 时,两者较为接近.(3)与Wang等[9]的1670MPa 级平行钢丝束相比,本文试验值与其较为接近,即使在相差最大的450℃时,两者也仅相差7.5%.(4)张昊宇等[18]选取同规格预应力钢绞线的中丝为试验对象,与本文试验数据相近.由于生产工艺的差异,本文平行钢丝束试件的名义屈服强度高温折减系数比热处理高强钢S460M[10]和S690QT[10]分别低89%与63%.

图7 平行钢丝束试件名义屈服强度高温折减系数试验值与 已有研究的比较Fig.7 Comparison of reduction factors of yield strength between test data and previous studies
3.3 弹性模量高温折减系数
图8为平行钢丝束试件弹性模量高温折减系数试验值与已有研究[8-10,17-18]的比较.由图8可见:(1)各已有研究的预应力钢索弹性模量高温折减系数较为离散.(2)本文试验数据与文献[9,18]比较接近;低于600℃时,随着温度的升高,本文试验数据与文献[8]建议值差值逐渐增加;到600℃时,因为钢丝的高温回复作用,使钢丝中的索氏体组织开始发生剧烈变化,平行钢丝束弹性模量逐渐降低,本文试验值比文献[8]建议值低53.1%. (3)与 钢绞线试验数据[17]相比,因平行钢丝束无钢丝缠绕效应,在 20~ 400℃时,本文试验值均低于预应力钢绞线的弹性模量高温折减系数,当温度超过400℃后,随着钢绞线的缠绕松弛,两者差异逐渐减小至3%. (4)当 温度高于400℃时,本文试验值远小于高强钢S460M[10]和S690QT[10]的弹性模量高温折减 系数.

图8 平行钢丝束试件弹性模量高温折减系数试验值与 已有研究的比较Fig.8 Comparison of reduction factors of elasticity modulus between test data and previous studies
3.4 比例极限高温折减系数
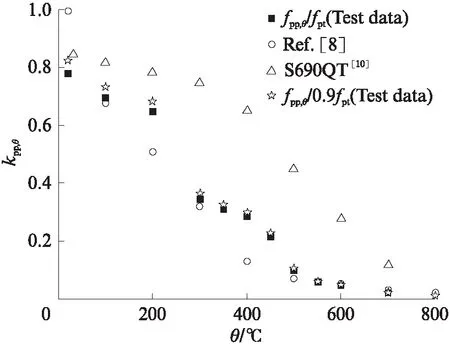
图9 平行钢丝束试件比例极限高温折减系数与已有 研究的比较Fig.9 Comparison of reduction factors of proportion limit between test data and previous studies
图9为平行钢丝束试件比例极限高温折减系数与已有研究[8,10]的比较.由图9可见:(1)在20℃时,本文试验值比文献[8]建议的比例极限高温折减系数低21.6%;在100~500℃时,则最大高54.0%. (2)本 文试验值远低于高强钢S690QT[10]的比例极限高温折减系数,在300℃时,差距高达84.5%,这是由于比例极限由fpp,θ=Ep,θ×εpp,θ得到,平行钢丝束在高温下弹性模量下降比高强钢快,但两者比例极限应变相近所致.
3.5 极限强度高温折减系数
图10为平行钢丝束试件极限强度高温折减系数试验值与已有研究[9,17]的比较.由图10可见:在20~800℃时,已有研究给出的平行钢丝束极限强度高温折减系数与本文试验值相差不大,与钢绞线在500℃时的试验数据[17]相差最大仅18%.
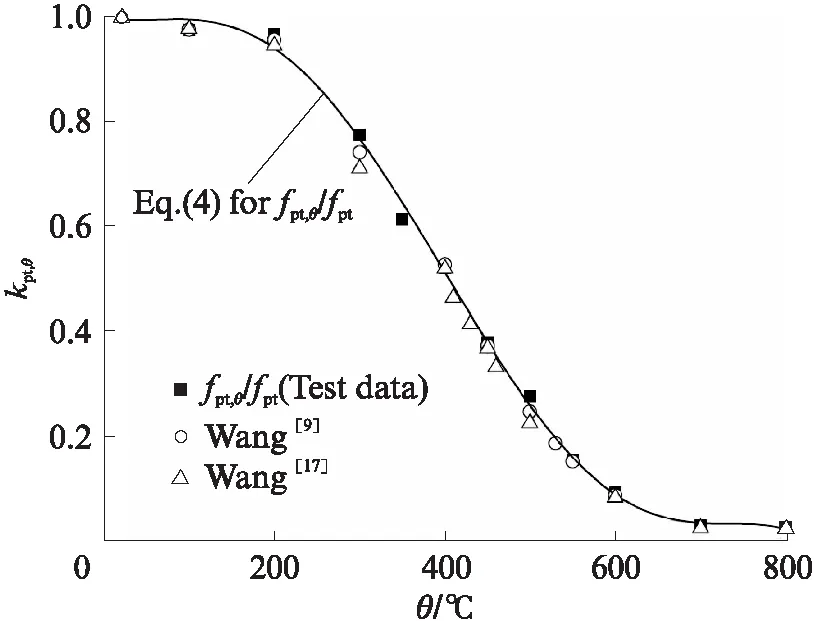
图10 平行钢丝束试件极限强度高温折减系数试验值与 已有研究的比较Fig.10 Comparison of reduction factors of ultimate strength between test data and previous studies
表3为各温度水平下平行钢丝束试件力学性能指标折减系数汇总.由表3可见:总体上,低于 300℃ 时,平行钢丝束试件的弹性模量衰减可忽略不计,而比例极限衰减明显;超过300℃时,试件各项力学性能衰减显著,特别是当温度超过600℃时,由于珠光体组织的滑移和相变,导致钢材的微观结构从铁素体-珠光体转换为奥氏体.所以,平行钢丝束试件应力-应变曲线随温度升高趋于平缓;极限应变、断裂应变随着温度的升高呈不同的增长趋势,而比例极限应变、屈服强度、弹性模量、比例极限以及极限强度呈下降趋势.
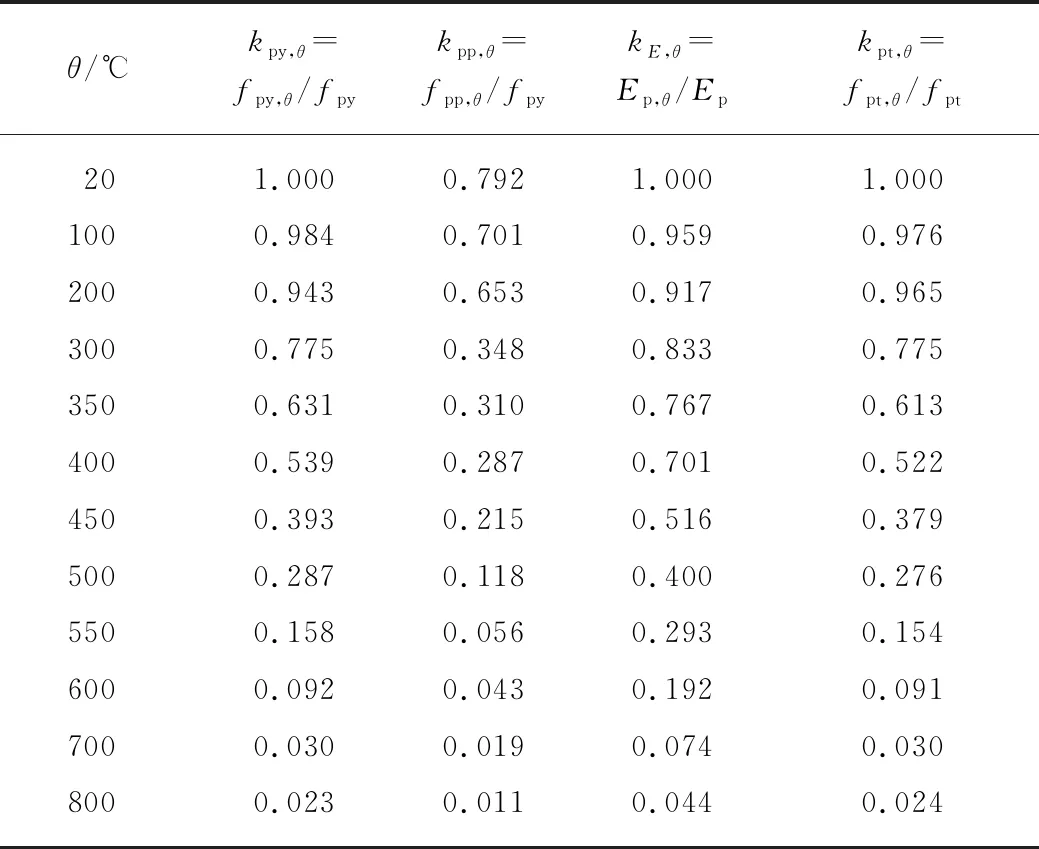
表3 各温度水平下平行钢丝束试件力学性能指标折减系数汇总
3.6 高温折减系数函数模型
基于试验数据,拟合出平行钢丝束试件各项力学性能指标的高温折减系数函数模型.
回归系数R2=0.9973下平行钢丝束试件的名义屈服强度高温折减系数表达式为:
fpy,θ/fpy=-2.629×10-14θ5+5.356×10-11θ4
-3.25×10-8θ3+4.689×10-6θ2
-8.457×10-4θ+1.018
(1)
回归系数R2=0.9970下平行钢丝束试件的比例极限高温折减系数表达式为:
fpp,θ/fpy=-1.972×10-15θ5-1.804×10-12θ4
+9.785×10-9θ3-6.917×10-6θ2
+4.274×10-5θ+0.780
(2)
回归系数R2=0.9970下平行钢丝束试件的弹性模量高温折减系数表达式为:
(3)
回归系数R2=0.9971下平行钢丝束试件的极限强度高温折减系数表达式为:
fpt,θ/fpt=-4.279×10-14θ5+8.508×10-11θ4-
5.156×10-8θ3+7.641×10-6θ2-
3.745×10-4θ+0.999
(4)
4 高温应力应变函数模型
根据本文试验数据,拟合出平行钢丝束试件的高温应力-应变全过程关系函数:
(5)
式中:a1、a2、a3、b1、b2和b3为拟合系数(见表4和 表5 ).

表4 拟合系数a1、a2、a3

表5 拟合系数b1、b2、b3
图11为平行钢丝束试件高温应力-应变曲线对比.由图11可见,平行钢丝束试件的高温应力-应变函数模型(式(5))与试验结果吻合较好.
文献[8]建议的钢索高温应力-应变关系模型中,没有考虑平行钢丝束的应力强化阶段,并且在100~200℃时,低估了7.1%的平行钢丝束极限强度.文献[8]规定名义应变到极限应变之间的屈服强度取定值,极限应变至断裂应变为斜线下降,这种简化关系与试验得到的全过程应力-应变关系相差较大.
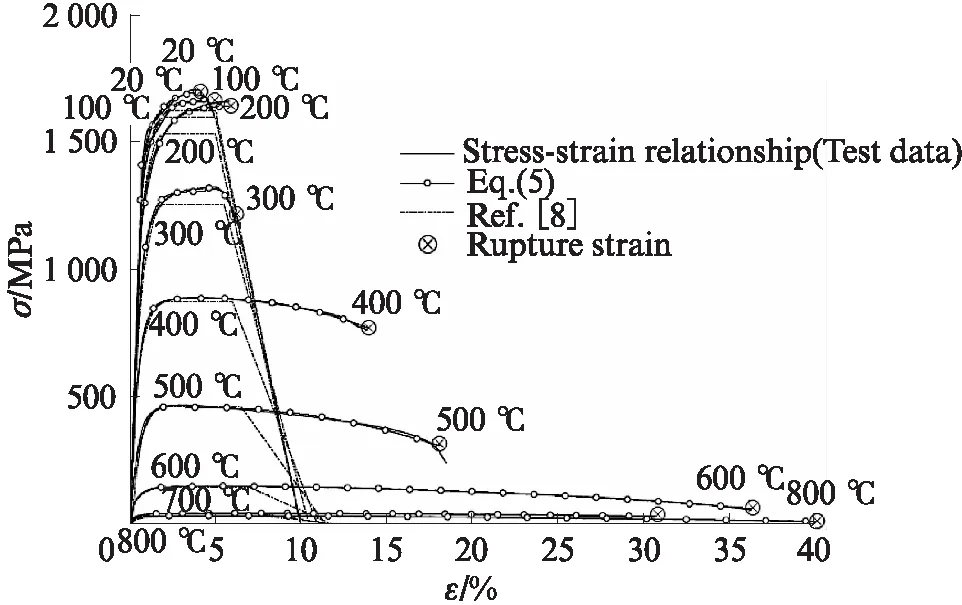
图11 平行钢丝束试件高温应力-应变曲线对比Fig.11 Comparison of stress-strain curves between test data and EN 1992-1-2
5 结论
(1)平行钢丝束极限应变试验值与文献中预应力混凝土用钢索取值相比,在20~200℃时基本接近;高于200℃后,本文试验值显著降低;平行钢丝束断裂应变试验值与文献建议值相比,在20~ 300℃ 时显著降低,在350~400℃时基本接近,在500~800℃时显著高于文献建议值.
(2)本文建议的平行钢丝束高温力学性能指标折减系数与高强钢试验数据相差较大;与文献中钢索的弹性模量折减系数及比例极限折减系数相差较大;当温度低于400℃时,与钢绞线相差较大;在100~200℃时,与已有平行钢丝束试验数据略有差异,与单丝试验数据相近.
(3)本文提出的平行钢丝束的各项高温力学性能指标,可服务于大跨度预应力张拉钢结构在火灾环境下的结构响应分析.
