基于线性自抗扰控制的光伏发电波动性消除方法研究

邹鹏辉

(国家电投集团青海光伏产业创新中心有限公司，西宁 810008)

0 引言

现阶段，光伏是新能源发电的重要组成部分。在实际运行的过程中，如果电网线路[1-2]出现故障，为了有效预防并网逆变器发生损坏，需要进行拖网运行。随着光伏发电系统中穿透率的持续增加，如果使用传统的控制方式则会导致并网点电压出现大幅度波动，系统的稳定性较差，所以要求全新的电网准则中并网电力系统一定具有低电压穿越能力，在系统发生故障期间能够对并网点电压提供支撑。

传统的光伏并网发电系统主要使用PID或者经过改进的PID控制方式[3]，虽然能够有效消除波动和降低误差，但是仍然存在以下缺陷，如：

(1)利用系统输出以及给定值进行比较得到误差，这样形成的误差偏大，而且容易引发超调。

(2)在积分反馈环节系统的响应速度大幅度降低，而且PID控制属于简单的线性加权控制，并不是最好的线性加权组合。

以上缺陷的存在会导致光伏发电系统发生故障，影响系统的综合性能[4-5]，甚至还会破坏系统的保护装置，造成系统脱网。

为了克服线性PID存在的不足，本文提出基于线性自抗扰控制的光伏发电波动性消除方法。通过具体的仿真实验数据，验证了所提方法的有效性以及优越性。

1 线性自抗扰控制策略

设定电网电压d轴为矢量定向[6]，则网侧变换器dq坐标系下的数学模型能够表示为以下的形式：

(1)

式中，id代表d轴的电流分量；iq代表q轴电流分量；ed代表d轴电网电压分量；eq代表q轴电网电压分量；ud代表d轴变换器侧端电压分量；uq代表变换器侧端电压分量；sd代表d轴的开关函数分量；sq代表q轴的开关函数分量,Lg代表电网电压基础分量，Rg代表电网电压侧分量，ω代表核定系数。

由于传统的光伏发电系统低电压穿越控制电压外环主要使用PI调节器[7-8]，为了得到更好的控制效果以及抗扰动性，本文使用LADRC(线性自抗扰控制)代替PI调节控制器，以下进行具体的分析。

2 基于线性自抗扰控制的光伏发电波动性消除方法

2.1 建立光伏发电系统的“抗扰范式”模型

根据线性自抗扰控制策略，以下重点针对光伏发电系统的“抗扰范式”展开研究，设定系统的总扰动为未知状态变量，利用ESO(扩张状态观测器)进行估计以及测试，同时将建模问题转化为状态估计。

为了方便进行抗扰范式组建，以下需要将三相光伏并网逆变器在dq坐标系下的数学模型进行转换，则有：

(2)

由于针对电压外环使用LADRC控制，所以：

(3)

由于逆变器的直流侧和交流侧有功功率的守恒原理，所以：

(4)

对式(4)进行变形，则：

(5)

将式(3)代入到式(5)中，则有：

(6)

将式(6)左右两边除以Cdc，则：

(7)

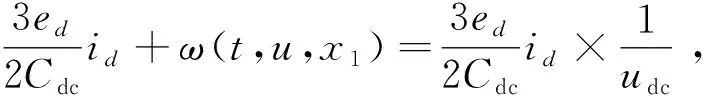
(8)

(9)

(10)

如果令f(t,u,x1)=ω(t,u,x1)+d(t)，总体代表其系统的总扰动量，ω(t,u,x1)代表系统的点控制量，d(t)代表光伏系统运行过程中所受到的外部扰动，bu代表控制量，将式(10)转换为光伏发电系统的“抗扰范式”模型，则有：

(11)

2.2 获取最优参数

虽然非线性自抗扰控制器能够实现光伏发电波动性消除，但是该控制器的内部结构过于复杂，导致系统的整体工作量大幅度增加，使其在实际工程中很少被应用。

针对以上缺陷，在组建光伏发电系统的“抗扰范式”模型的基础上，引入频率尺度变换，将LADRC一整套参数和控制器频率相关联[9-10]，通过LADRC技术实现参数整定，从而获取十分满意的控制效果。经过简化之后的自抗扰控制器主要由三个部分组成，分别为：

(1)线性扩张状态观测器；

(2)线性PD组合；

(3)扰动补偿环节。

光伏系统的被控对象表示为：

(12)

式中，f(y)代表未知函数；bu(t)代表控制增益；u(t)代表控制输入；ω(t)代表未知扰动，将其进行改写，则有：

(13)

其中式(13)的状态空间描述为：

(14)

其中：

(15)

(16)

(17)

C=[1,0,0,0] .

(18)

引入频率尺度变换，设计线性扩张状态观测器(LESO)，即：

(19)

式中，z代表x的估计值，即观测器的状态向量；L代表状态增益反馈矩阵[11-12]，需要通过控制对象进行设计。

将其写成矩阵的形式，则有：

(20)

通过线性ESO的带宽ω0进行参数整定，则有：

λESO(s)=s4+β1s3+β2s2+β3s+β4=(s+ω0)4.

(21)

求得：

β1=4ω0.

(22)

(23)

(24)

(25)

将自抗扰控制器的LESO输出进行转换，同时采用比例微积分控制器进行控制，即：

(26)

式中，kp，kd1，kd2代表PD的组合增益；一个包含扰动和不确定因素的复杂系统在经过扰动补偿之后，能够重新组建成一个简单的纯积分串联模式[13-14]，针对式(26)两边进行取拉式变换，则能够获取预期闭环函数为：

(27)

同理，将二阶闭环系统的分母极点配置在-ωc处，则有：

s3+kd2s2+kd1s+kp=(s+ωc)3.

(28)

线性自抗扰控制器中的参数为待整定参数，其中控制器中不同部分的控制参数的变化会给系统的控制效果[15]带来不同程度的影响，具体总结为以下几个步骤：

(1)通过系统标称参数计算b0；

(2)确定ESO带宽ω0和ωc之间的倍数关系；

(3)每一组选取一个ω0和ωc，按照前面的原则进行参数整定；

(4)按照对应的比例增大ω0和ωc，直至噪声无法承受系统输出波动或者振动再降低ω0和ωc的取值，这样可以兼顾系统的动态性能以及稳定性；

(5)适当降低不同参数的取值，但增大β4，直到在不形成超调的前提下，系统的闭环动态性能达到系统期望的状态，同时记录现阶段b0值所整定下的参数；

(6)需要适当调整kp，kd1，kd2的取值；

(7)不断调整b0，获取符合对应的取值，然后依据以上操作过程，直到获取一组较优的参数，以实现光伏发电波动性消除。

综上所述，基于线性自抗扰控制的光伏发电波动性消除方法的具体流程如图1所示。

3 实验结果与分析

3.1 测试装置与参数设置

为了验证所提基于线性自抗扰控制的光伏发电波动性消除方法的抗扰性以及可行性，通过MATLAB/Simulink 仿真软件进行仿真实验，实验环境为：Anaconda3.7，Python3.7以及Tensor Flow(2.0)。设置光伏阵列在标准光照下输出功率近似为40 kW，光伏电池开路电压为650 V，短路电流为63.3 A，MPPT电压为530 V，MPPT电流为65 A，直流母线电容为2 000 μF，PCC线电压有效值为380 V/50 Hz，直流卸荷电阻为21 Ω。由于控制器频率的波动性使得同步采样非常困难，因此采用准同步测试系统，根据快速测出的频率而选择合适的采样频率，使数据采样达到准同步。实验平台如图2所示。

其中测试系统为光伏谐波检测装置，频率计为SP3165B型多功能计数器，信号源为SYN5651型信号发生器。通过实验平台对频率计和测试系统软件界面上测得的频率进行对比，来测试系统对信号频率变化的检测准确度，从而保证采样数据的准确性和同步性。

3.2 A相电压

将未加入LADRC控制时网侧的A相电压和加入LADRC控制时网侧的A相电压进行对比，对比结果如图3所示。

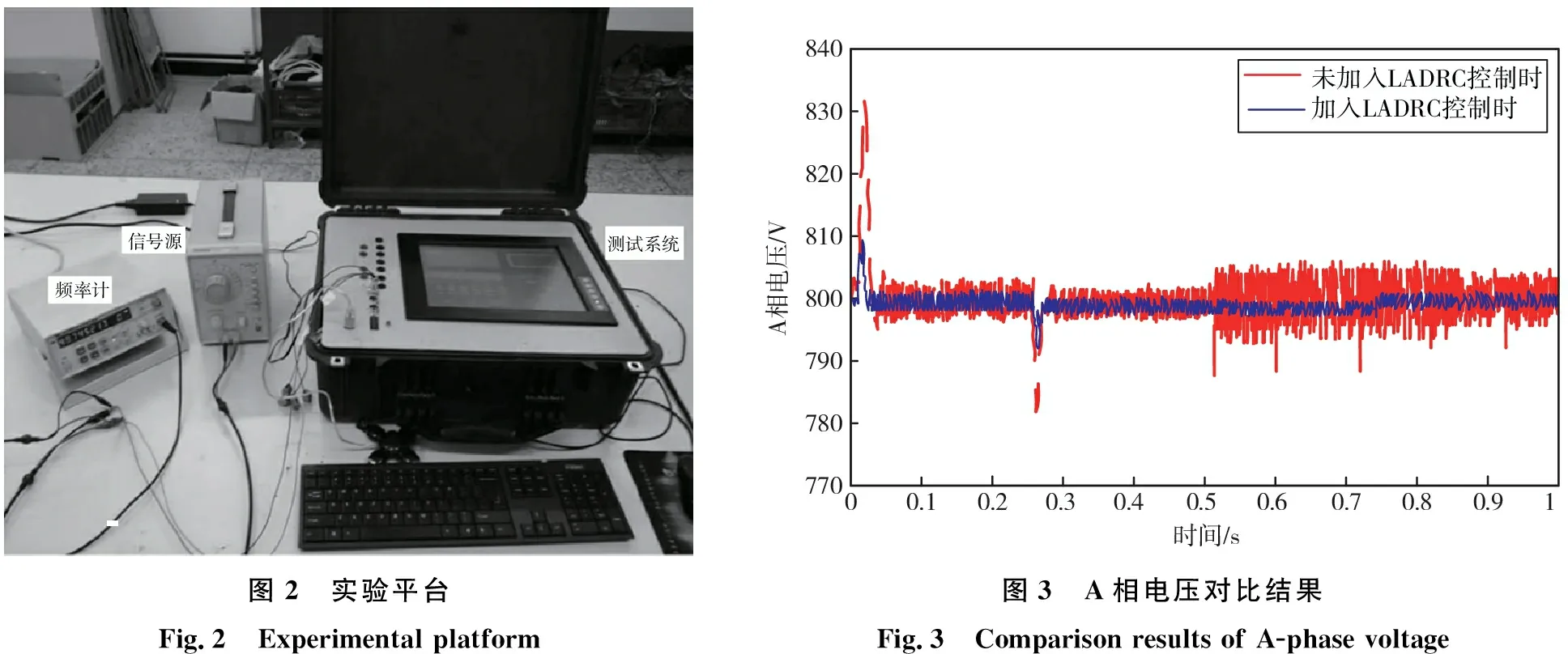
根据图3可知，未加入LADRC控制时网侧的A相电压波动在780 V～832 V范围内，冲击较大，由于有功功率的变化导致A相电压瞬间出现尖峰，而本文加入LADRC控制时网侧的A相电压波动较小，在790 V～810 V范围内，在可控范围内，抗扰动性能较好。

3.3 输出电流

将未加入LADRC控制时网侧的输出电流和加入LADRC控制时网侧的输出电流进行对比，对比结果如图4所示。

通过对比图4中的实验数据可知，采用LADRC进行控制时，输出电流在0～24 A范围内，较未加入LADRC控制的输出电流稳定，控制精度更高一些，控制效果更加理想，能够得到更好的补偿效果，实现光伏发电波动性消除。

3.4 有功功率

将未加入LADRC控制时网侧的有功功率和加入LADRC控制时网侧的有功功率进行对比，对比结果如图5所示。

根据图5可知，未加入LADRC控制时，网侧输出有功功率略有减少，加入LADRC控制时，当电网电压跌落，输出有功功率在0.25 s，0.65 s时呈现减少的趋势，能够消除光伏发电单元输出的有功功率。

3.5 执行效率

为了更进一步验证所提方法的有效性，对比未加入LADRC控制时的执行效率和加入LADRC控制时的执行效率，具体的实验对比结果如表1所示。

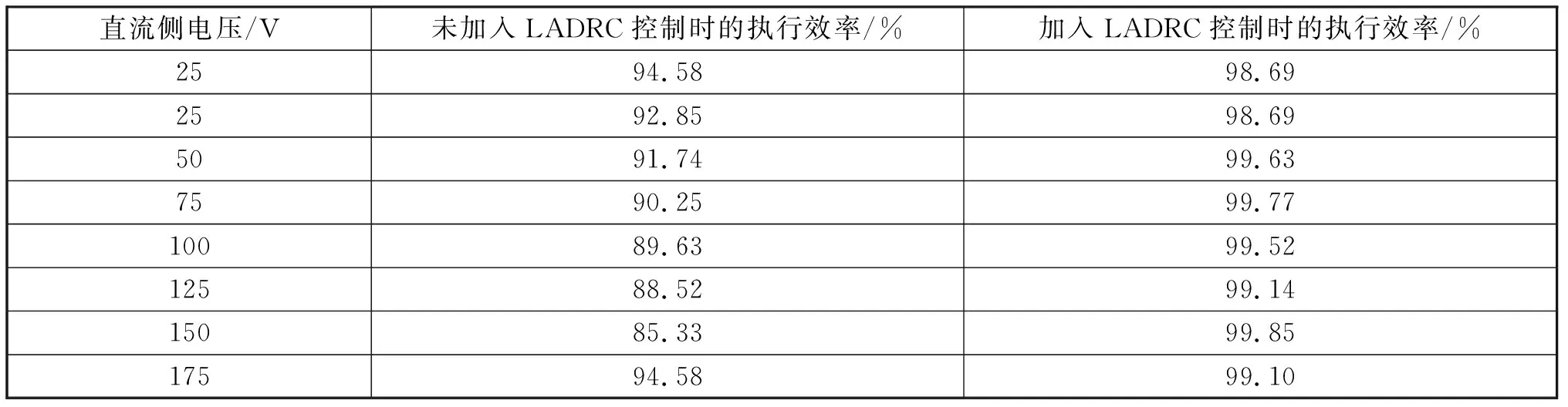
表1 执行效率对比结果

根据表1中的数据可知，加入LADRC控制时的执行效率最高可达99.85%，而未加入LADRC控制时的执行效率最高只有94.58%，加入LADRC控制时的执行效率比未加入LADRC控制时的执行效率高，说明本文方法的光伏发电波动性消除效果较好。

3.6 60 kW输出功率下的执行效率

当光伏阵列在标准光照下输出功率近似为60 kW时，测试未加入LADRC控制时的执行效率和加入LADRC控制时的执行效率，具体的实验对比结果如图6所示。

根据图6可知，在输出功率为60 kW时，未加入LADRC控制时的执行效率在24%～69%之间，曲线波动较大，而加入LADRC控制时的执行效率较平稳，在87%～90%之间。

综合分析上述表格中的实验数据和图中的数据可知，当输出功率为60 kW时，加入LADRC控制时的执行效率高，提高了光伏发电波动性消除效果，以上实验数据充分验证了所提方法的优越性。

4 结束语

为了提高光伏发电波动性消除效果，本文提出一种基于线性自抗扰控制的光伏发电波动性消除方法。将线性自抗扰控制参数与控制器频率相关联，促使线性自抗扰控制技术实现参数整定，从而消除光伏发电波动性。通过具体的仿真实验数据表明，本文方法具有较强的稳定性以及实用性。由于时间限制，导致所提方法仍然存在一定弊端，后续将进一步针对其进行进一步完善。