基于RLC电路非谐振频率工作点的磁感应耦合无线电能传输系统

王世伟，王首刚，赵立棣，裴 智，李客频，吕霞付

(1.重庆邮电大学 自动化学院，重庆 400065；2.华晨鑫源重庆汽车有限公司，重庆 401329)

0 引言

电磁感应耦合无线电能传输在大功率电动汽车无线充电，小功率移动设备充电，植入人体心脏起搏器电池充电，无线供电内窥镜等装置都已有应用[1-6]。电磁感应耦合无线传能系统可以分为电磁耦合和电场耦合两种耦合方式：电磁耦合通过线圈间的电磁感应实现无线传能,电场耦合通过电容间的交变电场实现能量传输。电磁感应耦合不在谐振状态时可以通过提高发送线圈的电压来实现提高传输功率和距离的要求，但需要克服接收端的反射阻抗和发送端线圈的感抗，所以常采用谐振补偿，通过谐振补偿在相同的传输功率条件下，传输距离和效率得到了极大的提高。因此，无线传能中的收发系统必须在谐振强耦合状态才能实现能量的远距离传输[7]。目前，对传能系统中发送端补偿电路的研究[8-11]都假设系统工作在谐振频率时，电感线圈和电容上产生的电压相等且最高，电感的电压与电流相位差为90°。然而，研究发现在RLC电路中电感L或电容C上产生最高电压的工作频率不是谐振频率[12]。这表明在传能系统中发送端工作的谐振频率并不是使得传能线圈产生最高电压的工作频率。另外,若需要检测发送系统的谐振状态须采集电压相位和电流相位两个信号进行比较。虽然电压很容易检测，但在检测电流时需要考虑电流信号的幅值变化和相位补偿问题[13-14]，这使得谐振状态的频率跟踪变得复杂。

针对以上问题，文中提出了一种基于RLC非谐振频率工作点的磁感应耦合无线电能传输系统。运用非谐振频率工作点，可以在发送线圈中得到比谐振频率点更高的电压，在接收线圈中可以产生更大的电流。运用此原理到无线传能系统中发送端RLC电路，发送线圈在非谐振时也会产生更高的交变电压。根据电磁感应理论，相同条件下感应端电流的大小与激励端电流大小正相关，当发送端线圈有更大电流流过时，接收端线圈亦可以感应到更大电流，无线传能系统可以传输更大功率。由于非谐振频率工作时发送线圈电压是最大值，所以，可以通过检测线圈电压来跟踪发送端工作频率，使得非谐振态跟踪的检测方法变得简单。文中首先设计了基于非谐振频率的电磁感应耦合传能电路S-P拓扑结构和补偿方案，然后对该系统的等效电路模型进行了分析，提出了非谐振频率工作点和补偿电容方案，并进行了补偿电容容量的计算，最后部分是仿真实验和实物实验及其结果分析，分析表明实验数据和仿真结果与理论分析基本一致。

1 基于非谐振频率工作点的磁感应耦合无线电能传输系统

基于非谐振率工作点的传能系统原理如图1所示，系统由发送端和接收端组成，发送侧的谐振电容CP,与发送线圈谐振电感LP组成谐振回路，接收端线圈和补偿电容参数与发送端相同。频率控制器产生方波驱动开关S1，S2，方波电压注入发送端谐振网络后在CP，LP回路中产生近似正弦的电流。接收端线圈LS通过磁场感应到交变电流，在线圈LS和CS产生谐振电压。接收端的谐振电压与耦合系数M、发送端线圈电流IP相关，电容CS上交变的电压通过D1,D2,D3,D4整流和Cf滤波后得到直流电压，电流IR流过负载RL做功完成电能传输。UDC是直流工作电压源，补偿电容CPS完成非谐振状态工作时的感性阻抗补偿。

2 系统建模与非谐振频率工作点分析

2.1 非谐振频率工作点的无线电能传输系统模型

图2所示为图1非谐振频率传能系统的等效电路模型.其中US是通过控制开关S1,S2后得到的方波电压源，Ue是吸收功率的负载电压源。RP是发送端回路电感和电容的等效电阻，RS是接收端回路总等效电阻，RL是负载电阻。非谐振频率工作点感应耦合电路模型为：

(1)

式中，“//”表示并联运算符。

发送端线圈电压与注入方波的角频率的关系为：

ULP=jωLPIP.

(2)

系统反射阻抗[15]为：

(3)

在工作频率一定的条件下，反射阻抗与耦合系数M相关。传能系统的发送线圈有交变的大电流流过时，接收线圈就可以感应到交变电流，收发线圈间的耦合模型如图3所示，磁感应耦合互感等效电路如图4所示。

Usi是发送线圈LP的激励源，当特定的方波电压注入发送线圈和谐振电容组成的LC回路时，在发送线圈LP中有近似正弦的电流IP流过。单匝圆形接收线圈LS与发送线圈LP间的互感系数是M则有：

(4)

式中，rP，rS是发送端和接收端线圈直径，k2=4α/(1+α)2+β2，α=rS/rP,β=h/rP；K(k)，E(k)分别是耦合系数的第一类和第二类椭圆积分，h为两线圈之间的距离，μ0为真空磁导率。

图3中当两线圈耦合时，由毕奥-萨伐尔定理可得自感磁通链:

(5)

互感磁通链：

(6)

其中,MSP=MPS=M。当激励源为正弦量稳态时，由式(5)、式(6)可得收发线圈的电压方程可表示为：

(7)

耦合电感LP,LS上的电压是电感自身的自感电压与感应得到的互感电压相叠加。

2.2 非谐振频率工作点分析

图4为发送端RLC等效电路模型，当发送线圈与补偿电容发生谐振时，串联回路中有近似正弦的电源US，CP是谐振电容，发送线圈感抗LP与反射阻抗ZR之和可等效为LPS，RP是RLC回路中的等效电阻的总和。电流源断开时RLC电路对外呈现的阻抗为：

(8)

设

(9)

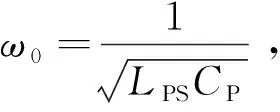
(10)

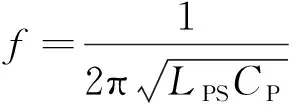
(11)

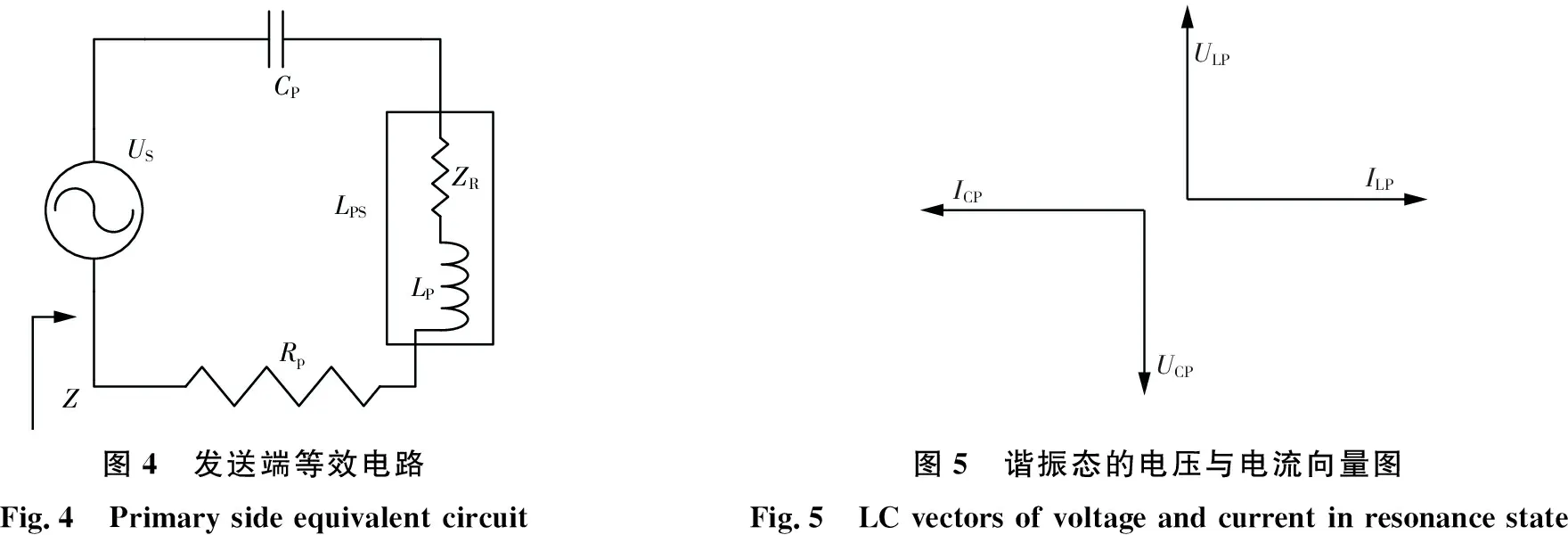
;3Q64$1-14-1;36-1*$16$1*-1图4 发送端等效电路 Fig.4 Primary side equivalent circuit图5 谐振态的电压与电流向量图Fig.5 LC vectors of voltage and current in resonance state

在感应耦合无线电能传输系统中，发送端的谐振电感作为发送线圈与接收端线圈耦合。发送端可以视为一个RLC谐振回路，分析时把接收端的反射阻抗[16-17]叠加在发送端电感上。由式(8)可得：

(12)

由式(12)推导串联谐振电路上电阻R，电感L和电容C上的频率特性，可得：

(13)

(14)

(15)

由式(13)—式(15)可知，在不同的非谐振频率下，电感和电容可以分别达到最大值，但这两个频率不相等，随着Q值不断提高两个频率点无限接近谐振频率。对式(13)—式(15)中的η求一阶导数并令一阶导数等于0，可以分别得电容上产生峰值时的频率为：

(16)

电感上产生峰值时的频率为：

(17)

使用MATLAB对式(13)—式(15)仿真，选取仿真参数Q=2可以得到图6。图中横坐标是工作频率与谐振频率的比值，纵坐标U/URLC是电源电压与RLC回路中电阻，电感，电容上分别产生的电压比值，图中三条曲线分别表示了每个器件上的电压与谐振频率偏移量的关系。UL曲线和UC曲线分别表示RLC谐振回路中电感和电容上的电压，当工作频率与谐振频率相同时，回路中电阻R上产生最高电压。当工作频率高于谐振频率时电感上产生的电压比谐振时更高，同理工作频率低于谐振频率时电容上产生的电压比谐振时要高。从图中可以看出在一定的频率范围内，电感电压随着频率变化关系的曲线是一个二次函数，所以只有一个极值点，可运用这个极值点斜率为零的特点来作为频率跟踪的目标。

从图6中可以看出，在RLC谐振电路中如果要使得电感L或者电容C上的电压达到极大值，需要注入两个非谐振频率到该电路中，这两个频率点分别位于谐振频率ω0点左右两端,ωC<ω0<ωL。定义ωC和ωL为非谐振工作频率工作点，它们是使得LC谐振回路在电容和电感上产生最高电压的两个工作频率。所以在无线传能系统中不同的耦合方式(电场耦合或磁场耦合)也应该有不同的传能工作频率点使发送线圈(电容极板)产生最高电压。

在发送端，工作在非谐振频率的RLC电路阻抗呈现感性，因此需要进行补偿，其补偿电路模型如图7所示，在图4的基础上增加了补偿电容CPS与RLC电路并联。阻抗ZP可以表示为：

(18)

其中虚部为：

(19)

当

(20)

可得发送端RLC非谐振频率工作点的补偿电容的容量为：

(21)

3 仿真实验

按照上述分析，使用LTspice仿真软件对图4模型电路仿真，仿真系统参数见表1所示，为便于分析和比较选取实验装置的实际值，由于存在反射阻抗所以选取的电感参数值比实验用测量值数据值要小。由公式(9)计算得到谐振频率将仿真参数代入系统仿真模型得到发送端线圈电压如图8所示。由公式(18)计算得到的非谐振频率参数代入仿真模型得到图9。比较图8和图9仿真结果，可以看出非谐振频率工作点在发送线圈上产生的电压VPP=256 V,比谐振频率工作点产生的电压VPP=250 V高。仿真结果与前面的理论分析一致。

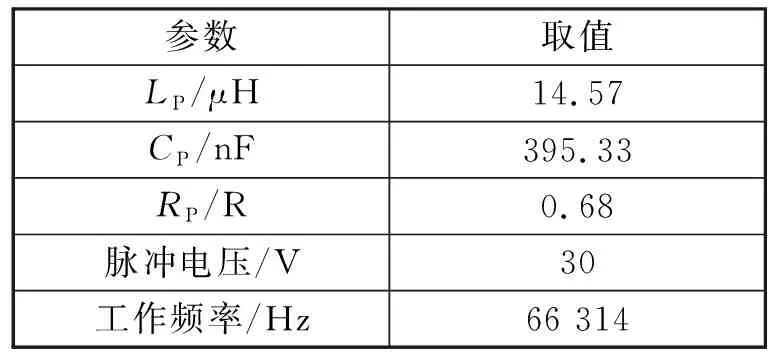
表1 LTspice仿真参数

4 实验验证

按照图1所示的系统拓扑和表2中参数，搭建基于非谐振频率工作点的磁感应耦合无线传能系统如图10所示。发送线圈LP由2股直径1 mm的漆包线并联绕制在内径15 cm外径20 cm的圆盘支架上。接收端LS用200股0.1 mm的漆包线并联的利兹线绕制在结构尺寸与发送线圈相同的支架上。谐振电容CP和CS选取耐压值1 000 V低于ESR电容。数字控制器STM32F407用于生成方波信号驱动变换器[18]的MOSFET有效工作，方波信号死区时间设计为200 ns，使用电子负载仪模拟负载变化，示波器ROHDE&SCHWARZ RTB2004测量发送端线圈的电流和电压以及它们的相位。

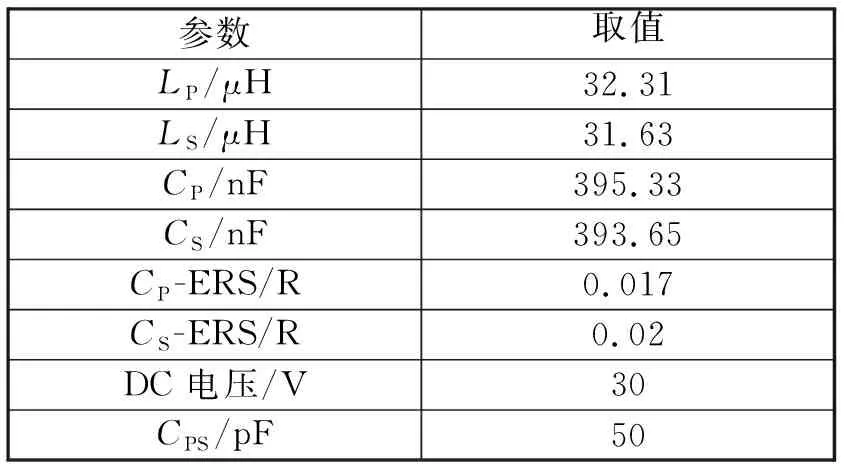
表2 实验系统参数

在谐振频率和非谐振频率工作条件下测试发送电圈电压和电流的实验波形如图11和图12所示。图中波形从上到下分别为C3线圈电流IP，C2线圈电压ULP，C1是变换器注入的方波电压US。示波器自动测量线圈电压和电流的峰值，及其相位差和频率，并显示在示波器下方表格。由于方波发生器频率调节精度的原因，实验中只捕获到了90.44°相位差的波形。实验波形显示：在非谐振频率工作点的线圈电压比谐振频率工作点的线圈电压高4 V。因此在线圈上有更大的交变电流流过，由于示波器电流自动测量只保留了小数点后一位，所以图中没有显示出小数点后面的变化。实验结果与仿真结果有差异主要是由于收发线圈间的耦合系数没有精确测量。仿真和实验证明了应用RLC电路工作的非谐振频率工作特性在无线传能系统中，实验显示非谐振频率工作时在发送线圈上产生比谐振频率时高出4 V的交变电压，在发送线圈中可以产生更大的电流，在远处的接收端可以感应到更强电流。

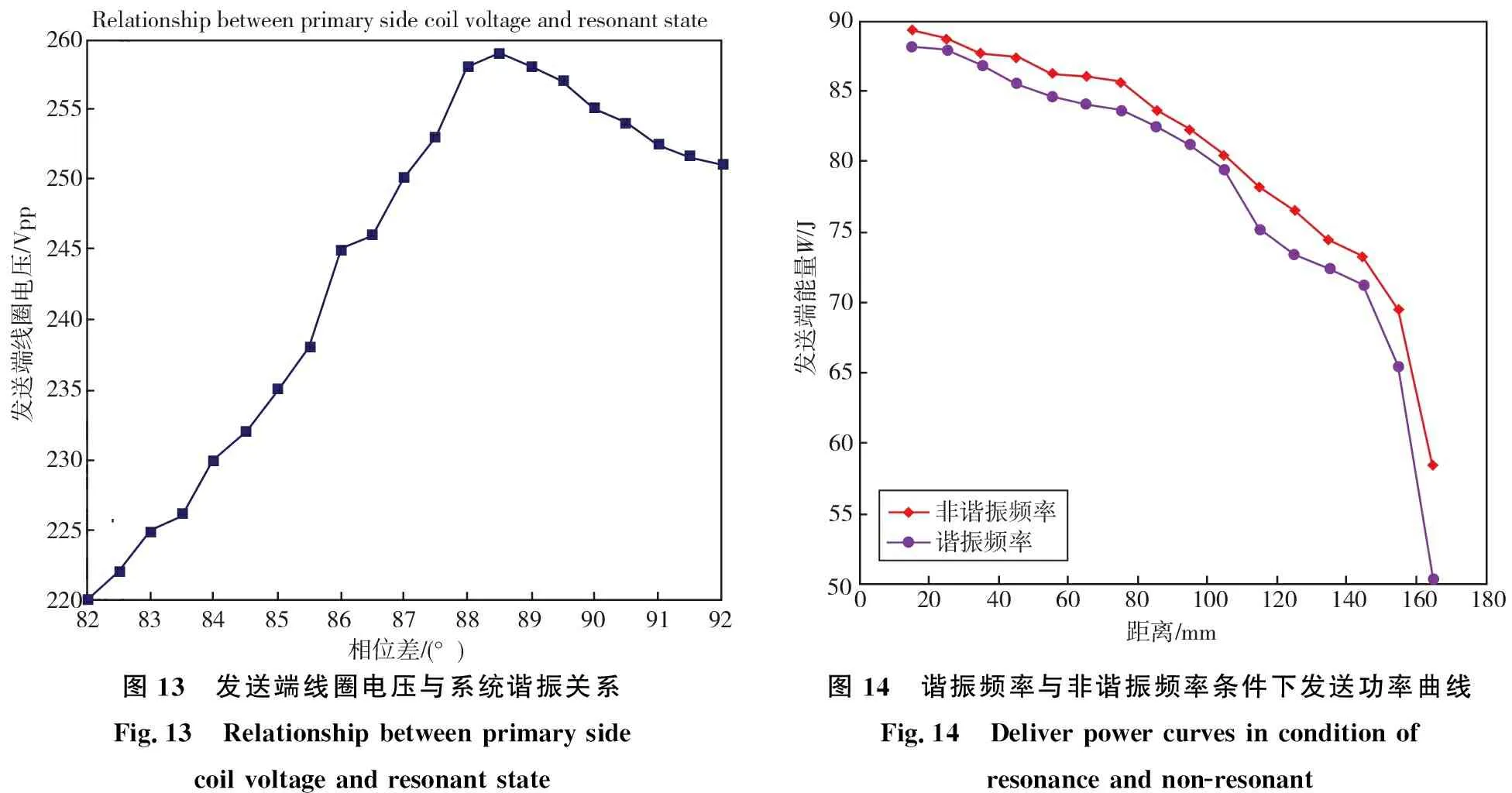
为了进一步验证非谐振频率工作点的理论分析，通过图10的实验平台，测试了发送端线圈上的电压与线圈电压电流相位差的关系如图13所示。图中纵坐标是发送线圈上的峰值电压，横坐标是线圈电压与电流的相位差。实验数据表明，在发送端的RLC谐振电路中注入不同的频率(如公式17)可以调节发送线圈电压，亦可以调节传能系统的传输功率；连续调节频率注入发送端变换器，线圈上的峰值电压从220 Vpp到260 Vpp变化,测量显示线圈上电压与电流相位差从82°到92°变化。当发送线圈上峰值电压最大值为258 V时，电压电流的相位差是88.5°而不是谐振态的90°，从而验证了非谐振频率工作时在电感上会产生更高的峰值电压。由式(5)—式(7)分析可以知道在接收端的线圈能感应到更大的电流。图14所示为谐振频率与非谐振频率工作时的输出功率比较结果，横坐标为传输距离，纵坐标为输出功率。通过调节变换器的工作频率使发送端线圈峰值电压达到最高时(视为非谐振频率工作状态)，此时测量输出功率如图中非谐振频率工作线所示。调节变换器工作频率使发送线圈的电压与电流相位差为90°(视为谐振频率工作状态)时测量其输出功率如图中谐振频率工作线所示。图14中实验数据表明，在非谐振频率工作点时负载不变的情形下，无线传能系统的发送端工作在非谐振状态时可以比谐振状态发送的功率高2%。

5 总结

基于RLC电路在非谐振频率点工作时电感上产生的电压比谐振时产生电压高的特点，文中提出了一种运行在非谐振频率工作点的磁感应耦合无线传能系统，传能系统工作和耦合的频率都用非谐振频率。文中给出了系统拓扑和拓扑电路模型，在分析了电路模型的非谐振频率工作点后，定义了两个非谐振频率工作点ωC和ωL，并给出了非谐振状态时感性电路的电容补偿方案和补偿电容计算方法。实验和仿真数据基本相同，实验数据显示运用非谐振频率的发射功率比谐振频率发送功率高2%。仿真和实验验证了该非谐振频率传能系统的有效性，非谐振态频率工作时有线圈电压最高特点，这为频率跟踪方法提供了一种新思路。文中提出的方法只对磁感应耦合做了研究，后续可应用该现象对电场耦合无线传能继续研究。