改进深层小波自编码器的轴承故障诊断方法
2020-03-11杜小磊陈志刚
杜小磊,陈志刚,许 旭,张 楠
1.北京建筑大学 机电与车辆工程学院,北京100044
2.北京建筑大学 北京市建筑安全监测工程技术研究中心,北京100044
1 引言
滚动轴承是旋转机械的重要部件,其健康状态对整机的性能、稳定性和寿命有着很大的影响,一旦出现故障,轻则降低生产质量,重则造成生产事故。因此,自动准确地识别滚动轴承的故障具有重要意义[1]。
实际采集到的轴承振动信号经常受到诸如多振源激励和响应相互耦合以及噪声干扰等因素的影响,常表现出强烈的非线性和非平稳性。在当今大数据时代,传统基于“特征提取+模式识别”的轴承故障诊断方法[2-4]已越来越不能满足自动化诊断要求[5]。
深度学习[6]克服了传统故障诊断方法的缺陷,能自动从原始数据中学习具有代表性的特征,很大程度上摆脱了对诊断专家信号处理经验的依赖,在轴承诊断领域得到了应用。文献[7]提出了一种基于深度自编码器(Deep Auto-Encoder,DAE)的轴承诊断方法,将轴承原始振动信号直接输入DAE 进行自动提取特征和分类。文献[8]将压缩感知技术与DAE结合对滚动轴承进行自动故障诊断,有效提高了网络的计算效率。文献[9]利用双树复小波对轴承振动信号进行特征提取,然后利用深度信念网络(Deep Belief Network,DBN)进行轴承诊断。上述研究均利用深度模型较好地实现了滚动轴承的智能诊断,但同时也存在一些问题:(1)DBN训练困难,初始权值具有指向性,易陷入局部最优[10]。(2)DAE 的隐层激活函数大多为Sigmoid 或Relu 函数,难以建立轴承故障与振动信号之间的精确映射关系[11]。(3)在对上述深度模型参数进行微调时,易产生梯度消失现象,使网络不能进行高效的学习,且上述模型所使用的损失函数均为均方误差损失函数,对轴承复杂振动信号的特征学习鲁棒性低[12]。小波函数包含尺度因子和位移因子,位移因子使小波沿信号的时间轴进行遍历性分析,尺度因子用于分析信号不同的频率,因此,利用小波函数作为自编码器(Auto-Encoder,AE)的激活函数,设计小波自编码器(Wavelet Auto-Encoder,WAE)进而构造深层小波自编码器(Deep Wavelet Auto-Encoder,DWAE),能更好地实现对轴承原始振动数据的无监督特征学习。针对深层网络的梯度消失现象,文献[13]引入“跨层”连接,建立ResNet网络提高了遥感图像的识别率。
针对上述问题,本文利用小波函数多尺度和多分辨的特性构造WAE,改进WAE的误差函数并引入收缩自编码机制以增强网络的鲁棒性,且引入“跨层”连接缓解DWAE的梯度消失现象,较好地实现了滚动轴承的智能故障诊断。
2 改进深层小波自编码器
2.1 小波自编码器
WAE 结合了小波函数的时频局部特性和AE 的自动特征提取的优点,使用小波函数代替AE 的Sigmoid函数,增强了网络的特征提取性能。DWAE 由多个WAE构成,标准WAE和2隐层DWAE的结构如图1。
设WAE 输入层有m 个节点,隐层有L 个节点,输出层有m 个节点,给定m 维输入向量x=[x1,x2,…,xm]T,隐层小波节点j 的输出hj如下:

式中,Wjk为隐层小波节点j 和输入层节点k 之间的连接权值,aj为隐层小波节点j 的尺度因子,cj为隐层小波节点j 的平移因子,ψ 为Morlet 小波的实部,表达式如下:

则隐层小波节点j 的输出改写为:
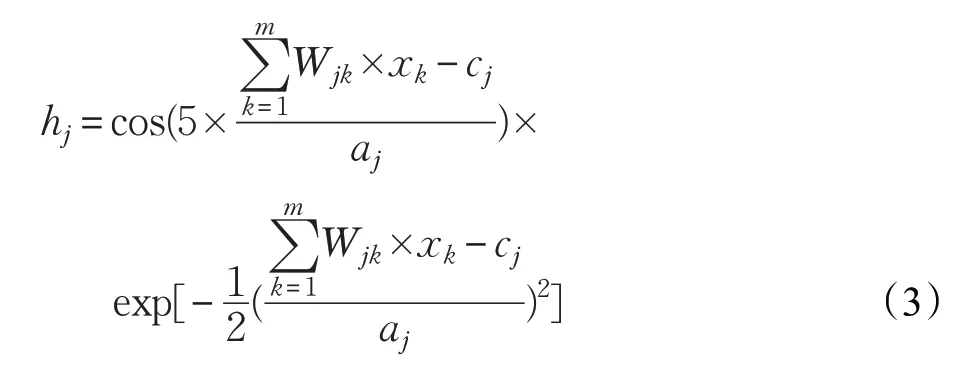
式中,Wij为隐层小波节点j 与输出层节点i 之间的连接权值。
则输出层节点i 的输出如下:
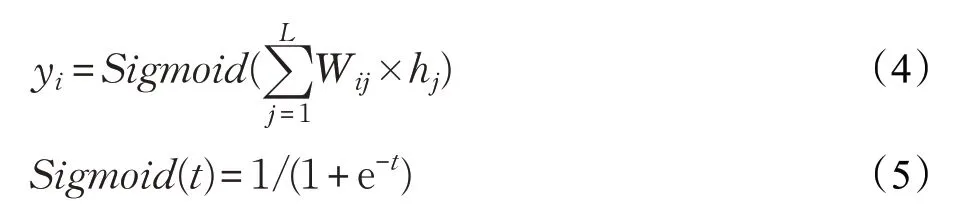
训练WAE 就是不断地调整参数,最后找到一组最优参数{Wij,Wjk,aj,cj},使输入和输出之间的损失函数最小化。DWAE堆叠多个WAE,采取逐层训练方法,将上一级WAE的隐层输出作为下一级WAE的输入,同时保证损失函数最小化,从而构成多层次的网络结构,直到整个DWAE完成训练。为进一步优化所提取的特征,在DWAE 最后一层加上有监督Softmax 分类器[14],将带有标签的少量样本结合BP 算法进行微调。标准WAE抗噪能力弱,泛化能力弱,易陷入过拟合,因此,改进WAE的误差函数并引入收缩自编码机制,详细如下:
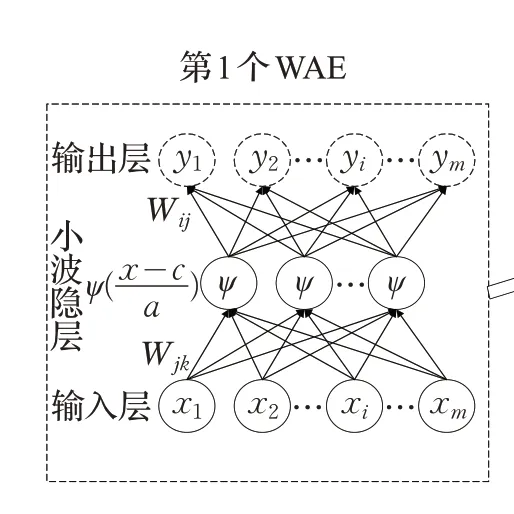
图1(a) WAE
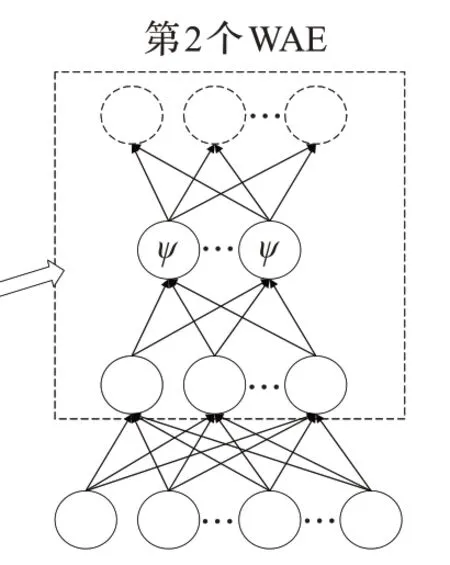
图1(b) 2层WAE堆叠的DWAE
(1)标准WAE的损失函数为均方误差函数,对复杂振动信号的特征学习鲁棒性低。而最大相关熵损失函数[12]对复杂非平稳背景噪声不敏感,具有与复杂信号特征相匹配的潜力。设两个随机变量A=[a1,a2,…,am]T,B=[b1,b2,…,bm]T,相关熵的近似计算如下:
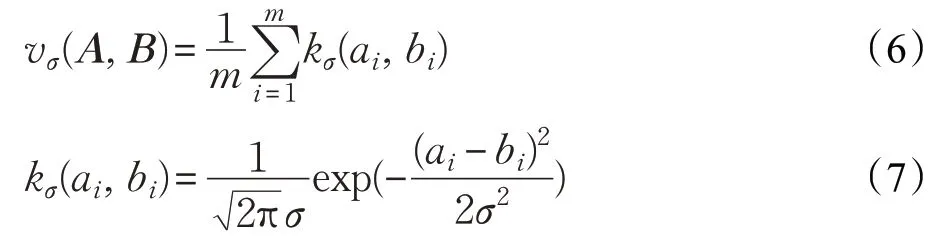
式中,σ 为高斯核函数尺寸。
则WAE损失函数最小化可以通过最大化以下函数实现:

式中,m 为样本个数,xi为输入样本向量,yi为输出向量。
(2)收缩自编码机制。收缩自编码[15](Contractive Auto-Encoder,CAE)通过增加收缩惩罚项学习信号的鲁棒性特征。收缩惩罚项如下:
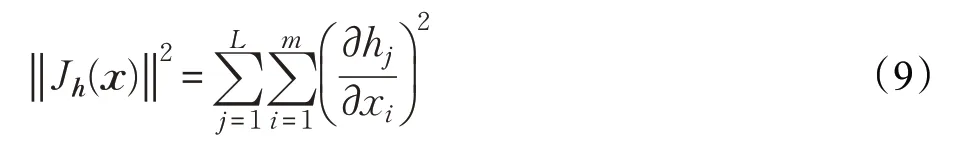
通过最小化式(9),使网络学到的隐层表示对输入的狭小变动具有较强的鲁棒性。则改进后的WAE的损失函数如下:

式中,λ1为收缩惩罚项系数,λ2为权重衰减项系数,Dm为m 个输入样本集合,sl为第l 层的节点个数(s1=s3=m,s2=L),W(l)IJ为第l 层权重,。
WAE的参数更新公式一般如下:
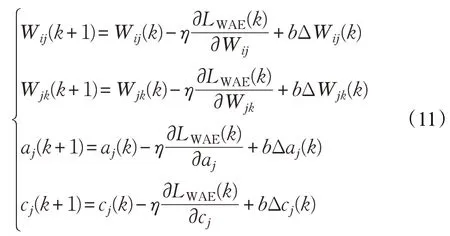
式中,η 为学习率,b 为动量项系数,LWAE(k)为WAE的第k 次迭代的误差。
在式(11)中,η 是一个全局性的常数,当η 过大不利于收敛,η 过小需要太多的训练时间。为了解决上述问题,引入自适应学习率,以cj的更新为例,计算公式如下:

式中,1 <α <2。
2.2 “跨层”机制
ResNet 使用“跨层”连接有效缓解了深层网络因梯度消失带来的性能退化问题。因此,为了提高DWAE的性能,将“跨层”连接引入DWAE,“跨层”DWAE 结构如图2(a)所示。图2(a)为单“跨层“DWAE 网络,可看作一个深DWAE 网络与一个浅DWAE 网络耦合形成,如图2(b)。
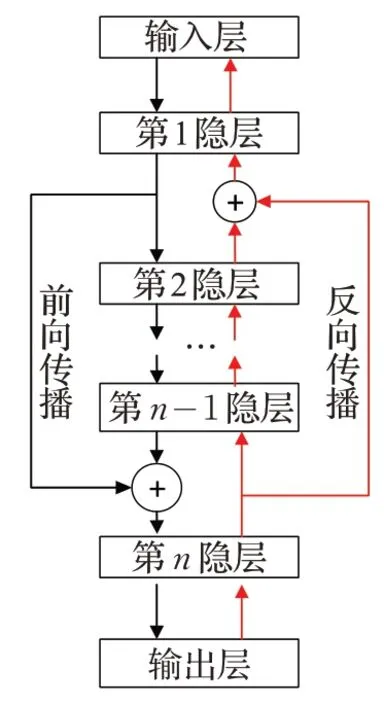
图2(a)“跨层”DWAE结构
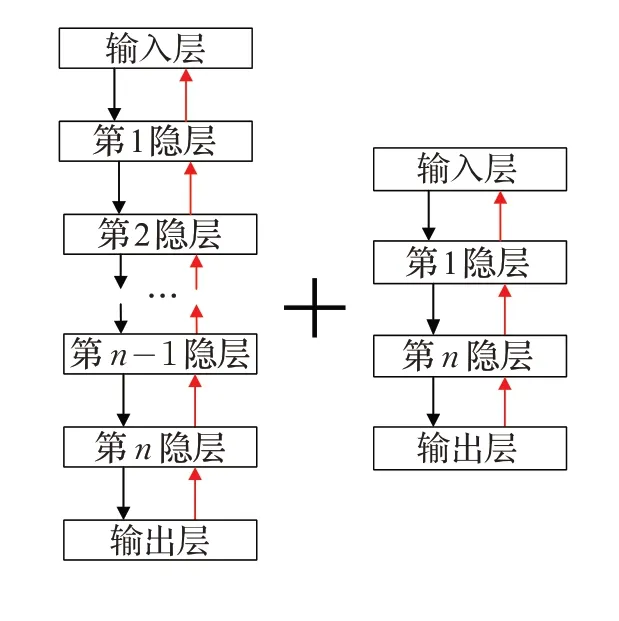
图2(b)“跨层”DWAE所拆分的两个网络结构
考虑DWAE 网络不同层次的特征在轴承故障识别中的贡献,定义“⊕”处的传播方式如下:
(1)前向传播
轴承训练数据进入输入层后,在第1隐层上产生一条辅线,将其提取的特征与第n-1 个隐层提取的特征联立,作为第n 个隐层的输入,如下:

式中,Hn为第n 隐层的特征矩阵,H1为第1 隐层的特征矩阵,Hn-1为第n-1 隐层的特征矩阵。
(2)反向传播

式中,G1为第1隐层的梯度矩阵,G2为第2隐层的梯度矩阵,Gn为第n 隐层的梯度矩阵,c 和d 为主线和辅线的梯度矩阵耦合比例,用(c:d)表示,c+d=1。
综上,本文方法主要步骤如下:
(1)利用传感器采集轴承各工况振动数据。
(2)将振动数据随机选取70%作为训练数据,剩余的作为测试数据,对训练数据、测试数据分别归一化到[0,1]。
(3)利用Morlet 小波作为激活函数设计改进的WAE,并进一步构造”跨层”连接的DWAE。
(4)将归一化后的训练数据以无监督方式逐层训练WAE,将上一级WAE 隐层输出作为下一级WAE 的输入,逐层提取特征信息,将最后一级WAE的隐层输出作为Softmax的输入,通过有监督BP算法结合少量带标签样本微调整个DWAE。
(5)根据测试结果判断是否满足实际期望的诊断效果,如果诊断正确率过低则修正网络,再重复步骤(3)和步骤(4),直到达到预期精度。
3 实验验证
3.1 实验数据初步分析
为验证本文方法的有效性,以轴承实验台为对象,采集不同故障类型和不同故障程度的轴承振动信号。实验台如图3,由驱动器、齿轮箱、测试轴承和负载等组成,传感器置于轴承座上,使用电火花技术在轴承的内圈、外圈和滚动体上加工故障直径分别为0.16 mm 和0.32 mm 的切槽,采样频率为12 kHz。在2 000 r/min 和1 400 r/min、负载1 hp 工况下采集轴承振动数据,最后得到每种工况下1 000个样本,每个样本由1 024个采样数据点组成。表1 为7 种轴承工况,包括4 种单一故障和2种复合故障。为减小噪声干扰,将轴承原始振动数据归一化到[0,1]。图4 为轴承7 种工况的时域图和频域图,由时域图可知,轴承内圈和外圈故障振动信号有周期性冲击成分出现,且比复合故障下的冲击明显,但早期故障信号受噪声干扰严重,部分冲击淹没在噪声中,振动情况较为复杂,难以区分轴承故障类型及故障程度。从频域图可以看出同种故障类型的频谱有一定的差异,但是对于同种故障类型但不同程度的故障,从频谱上很难区分。且由于传统特征提取方法的不确定性和复杂性,使得轴承早期轻微故障特征和复合故障特征难以提取,致使故障诊断的难度很大。因此有必要引入深度学习进行逐层特征提取以建立各种故障状态与输入信号之间的精确映射关系。

图3 轴承故障诊断实验台
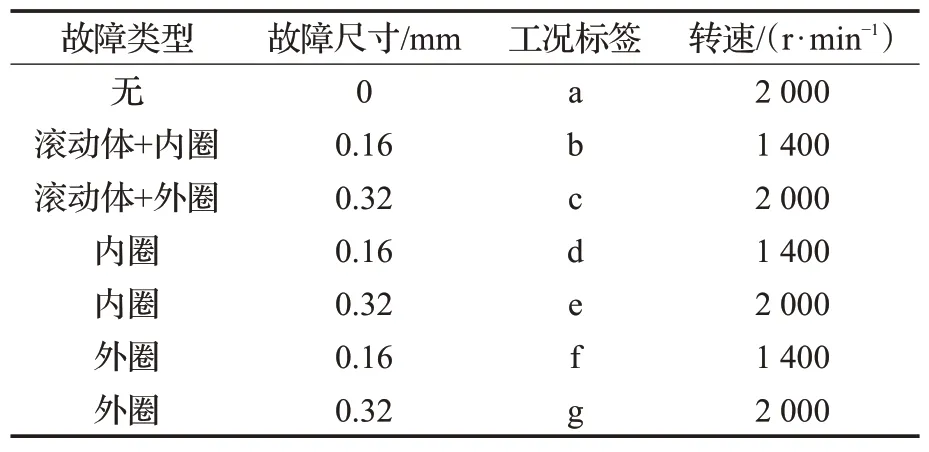
表1 7种轴承工况
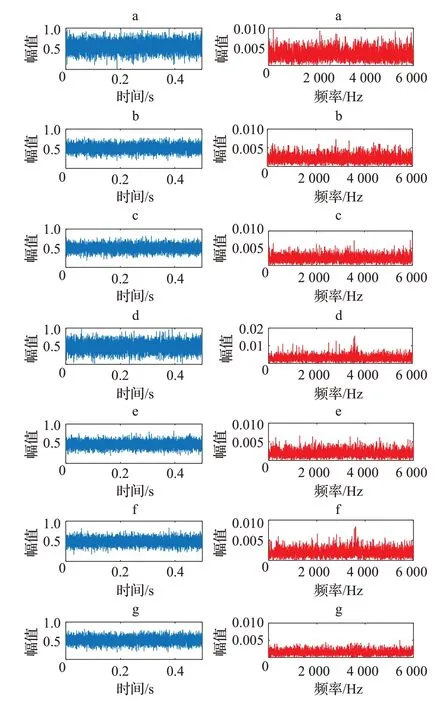
图4 轴承7种工况时域图和频域图
3.2 诊断结果与分析
为证明本文方法的优越性,采用人工神经网络(Artificial Neural Network,ANN)、支持向量机(Support Vector Machine,SVM)2 种传统智能诊断方法和标准DAE(Sigmoid 激活函数)、DBN 和不加“跨层”连接的DWAE 3 种深度学习方法进行分析比较。与传统智能诊断方法不同,本文方法无需对信号进行特征提取,输入始终是1 024 维振动数据。ANN 和SVM 的输入分为2 类,第一类是1 024 维振动数据,第二类是均方值、均值、方差等24个特征参数,这24个特性参数的详细计算见文献[16]。本文方法的参数列于表2,网络结构为1 024-512-256-128-64-32-7,由文献[17]所提方法确定,λ1、λ2、c 和d 等超参数的设置由文献[18]所提的粒子群算法确定。其他方法的主要参数见表3,其中ANN结构参数由反复实验确定;SVM 结构参数由10 折交叉验证法确定;DAE、DBN和无“跨层”连接DWAE网络结构由文献[17]确定,超参数由文献[18]所提方法确定。

表2 本文方法的参数

表3 其他方法的参数
为证明本文方法的稳定性,共进行5 次实验。图5显示每次实验的诊断结果,平均测试准确率见表4。由图5,本文方法每次测试的准确率分别为98.72%、99.16%、98.93%、98.85%和99.23%,均高于其他方法,由表4 可知,本文方法的平均诊断准确率为98.86%,高于标准DAE(91.25%)、DBN(90.13%)和无“跨层”连接的DWAE(94.32%),远高于方法2 的ANN(51.15%)和方法4 的SVM(53.19%)。提取24 个特征后,ANN 和SVM 的平均诊断准确率提高到76.57%和83.49%,但平均测试正确率仍低于本文方法。此外,本文方法的标准偏差为0.09,均小于其他几种方法。表5给出了所有方法(Corei7,16 GB 内存)的平均训练时间和平均识别时间,本文方法的平均训练时间为129.23 s,平均识别时间仅0.049 s。图6 给出了本文方法第一次测试的多分类混淆矩阵,可知复合故障状态b 和c 的分类正确率较低。
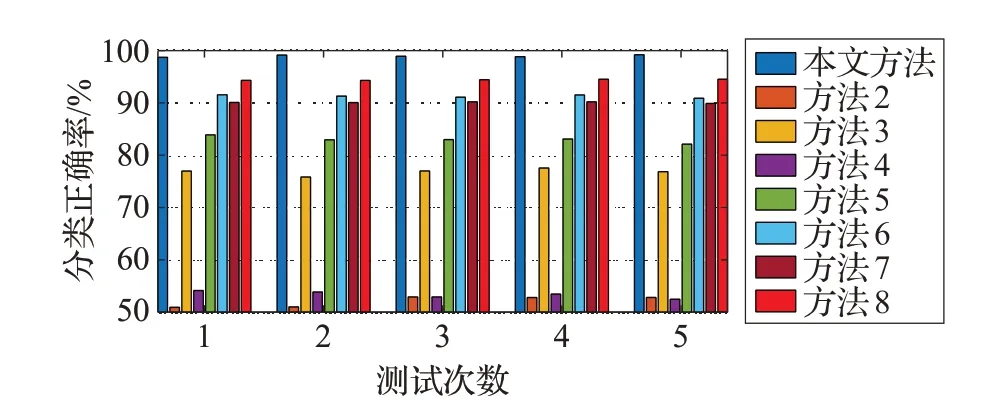
图5 不同方法的5次测试结果

表4 不同方法的诊断结果

表5 不同方法的平均计算时间s
收缩惩罚项系数λ1和权重衰减项系数λ2的适当选取既可以增强网络的特征提取性能,防止过拟合,又能加快计算。本文根据经验取λ1在0.01~0.09 和λ2在0.001~0.009 范围内进行研究,如图7 和图8,结果表明λ1=0.04 和λ2=0.003 有助于DWAE取得更好的性能。
研究发现主、辅线的耦合比例c∶d 对DWAE 的性能有一定影响,本文以c+d=1 为约束条件,以0.1 为间隔,分析不同耦合比例对DWAE 识别性能的影响,实验结果如图9,可知c∶d=0.2∶0.8时网络具有更优的性能。
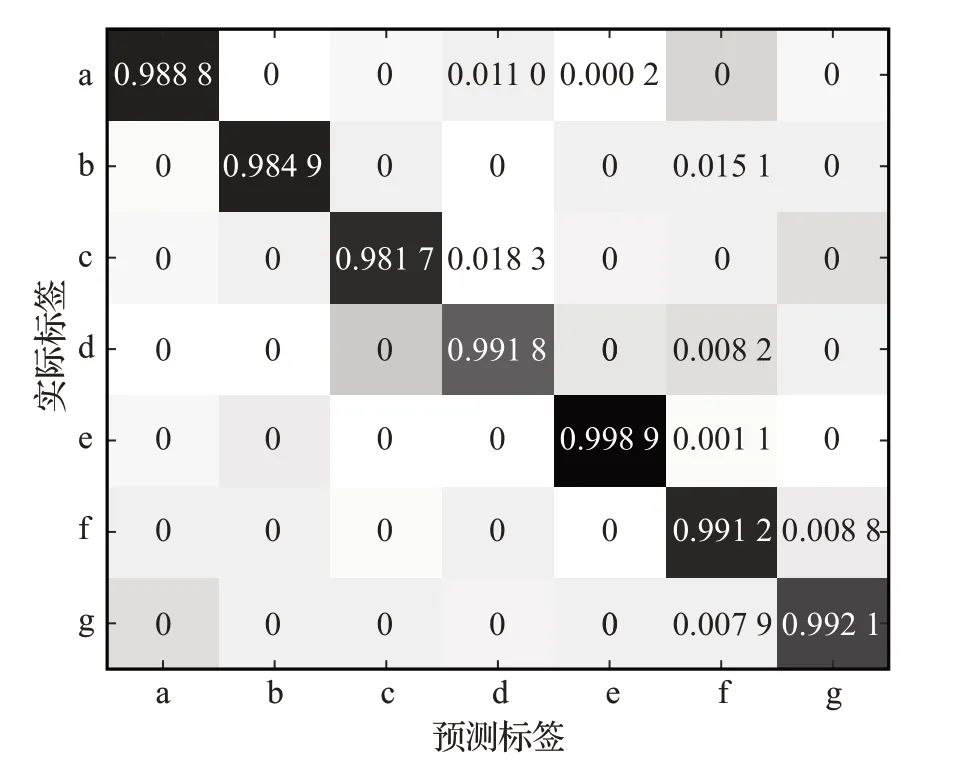
图6 多分类混淆矩阵
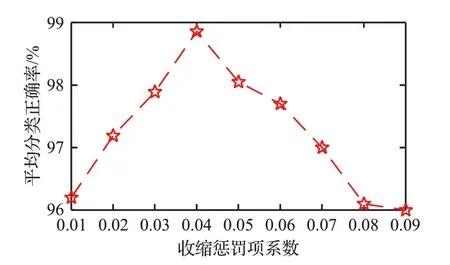
图7 λ1 对DWAE平均测试准确率的影响

图8 λ2 对DWAE平均测试准确率的影响
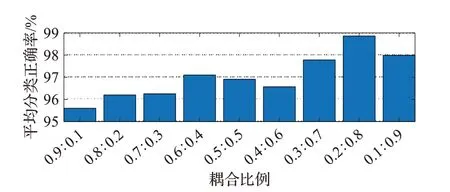
图9 主、辅线耦合比例对DWAE性能的影响
为直观显示DWAE所提取的特征,以轴承正常状态和外圈故障振动信号为例,由于网络所提取的深层特征较抽象,因此本文只给出DWAE提取的第1隐层的特征(以序列方式),如图10 和图11,可以看出,DWAE 所提取的第1隐层的特征从不同角度表现原始信号,这些特征比较好地满足了Fisher 判别准则[19],更有利于最后的分类。

图10 DWAE提取的轴承正常状态信号第1隐层特征图
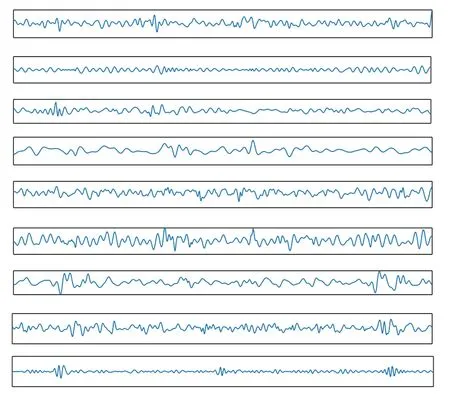
图11 DWAE提取的轴承外圈故障信号第1隐层特征图
4 结论
提出一种改进深层小波自编码器的轴承故障诊断方法,能有效地对轴承原始振动信号进行自动特征提取与故障识别,结论如下:
(1)将深度学习和小波理论相结合,增加了对信号的时频局部特性的表示,增强了网络自动提取特征的能力,改进WAE的误差函数和参数更新算法,并引入收缩自编码机制,使网络对信号的特征学习的鲁棒性大大增强。
(2)在DWAE的基础上,引入“跨层”连接,在一定程度上缓解了网络的梯度消失现象,并以实验证明了“跨层”连接的有效性。
