分形维数的全局点云初始配准算法

封雪梅，张志毅，杨 龙

西北农林科技大学 信息工程学院，陕西 杨凌712100

1 引言

随着三维成像技术如激光雷达和结构光主动成像等的快速发展，从实物模型构建数字模型得到更加广泛的应用。由于受到实物自身形状和观察方向的限制，需要从不同角度扫描实物，获得多角度扫描数据。这些扫描数据之间包含一定的公共部分，但是几何位置位于不同的坐标系下。点云数据配准就是依据已经存在的公共部分，将各个视角得到的扫描数据统一到相同的坐标系下，以得到完整的三维点云模型[1]。

文献[2]提出了全局配准算法——全局最优迭代最近点（Global optimal Iterative Closest Point，Go-ICP）算法。Go-ICP算法将一个半径为π 的球映射为旋转解空间，将单位立方体映射为平移解空间，利用分枝限界法求解变换矩阵最优解。Go-ICP 算法解决了传统ICP算法容易陷于局部最小值的缺陷，对于部分角度的点云与完整模型的点云之间的配准问题和重叠率很高的点云数据之间的配准问题都能达到很好的效果，但是不能很好地解决重叠率低的点云数据之间的配准问题。

针对点云初始配准算法，一方面采用基于随机抽样一致性算法进行初始配准；另一方面采用基于点云几何特征，从点云中提取特征点进行初始配准。基于随机抽样一致性算法的思想，文献[3]提出了初始配准算法——4PCS（4-Points Congruent Sets）算法，利用刚体变换保持相交线段的交比不变的性质，在点云P 上选取共面的4点作为基底，然后在点云Q 上寻找所有与该基底近似全等的共面4点集合，进行配准。此算法能够对大多数的点云数据进行较好的配准，但是对于某些存在大量平面的点云数据的配准效果有待提高。为了提高配准效率，文献[4]在此基础上进行了改进，提出了Super-4PCS算法，进行点云初始配准。基于点云几何特征的思想，文献[5]提出了初始配准算法，通过邻域拟合计算点云中点的曲率值信息，通过形状因子（Shape Index，SI）筛选关键点，构建局部参考框架，提取点云中的局部特征点，进行点云初始配准。采用邻域拟合计算点云中的曲率信息，是将连续的数学曲面理论应用于离散的点云数据中，是一种启发式的思想，理论依据有待提高。文献[6]提出通过中心点的邻域协方差矩阵来获得中心点的法向量信息，利用法向量以及归一化的特征值的变化量等相关信息作为特征描述符，获得最初的匹配点对；再利用传播机制，即在一个正确的匹配点对周围聚集更多正确的匹配点对，在一个错误的匹配点对周围不会聚集更多的正确匹配点对，从最初的匹配点对中筛选出较高精度的匹配点对进行初始配准；然后采用剪枝迭代最近点（Trimmed Iterative Closest Point，Trimmed-ICP）细配准算法进行配准。此算法采用邻域的协方差矩阵获得对应点处的法向量有一定的理论依据；针对邻域半径不能确定的问题，采用多尺度邻域半径计算得到多组法向量；然而如何获得最佳邻域来计算对应的协方差矩阵，获得较为准确的法向量信息，从而减少噪声点的影响还值得进一步研究。文献[7]提出基于沃罗诺伊图的方法从点云中提取特征点，此方法可以从完整的点云模型中提取出较尖锐的特征点，能够从部分角度的点云数据中提取出完整的轮廓边界线特征，但是不能很好地从部分角度的点云数据中提取出内部特征。文献[8]提出了一种基于熵和粒子群的三维点云配准算法，该算法可以有效地抑制噪声并提高配准精度。文献[9]提出了一种基于硬分配和软分配的方法，在重叠百分比较低时，实现点云的良好配准。

针对细配准算法，对于文献[10]提出的传统迭代最近点（Iterative Closest Point，ICP）算法，文献[11]提出了剪枝迭代最近点（Trimmed-ICP）算法，增强了ICP 算法的抗噪性和鲁棒性。文献[12]在传统ICP 算法基础上，优化目标函数，使对应点之间的距离中零距离的数量最大化，来确定对应点，进行精细配准。

分形理论是由Mandelbrot 提出并建立的理论体系[13]。维数是分形几何的中心概念，而Hausdorff维数是分形维数的重要内容[14]。维数大多应用在图像特征计盒维数方面[15-17]。分形维数是用来衡量自然界不规则程度的度量参数[13]，例如分形维数可以对非光滑、非规则、破碎等极其复杂的分形体进行定量刻画。分形维数参数，表征了分形体的复杂程度和粗糙程度，即分形维数极大或极小，则分形体越不规则、越复杂[18]。因此点云数据中不同的结构和形状对应着不同的分形维数。

针对Go-ICP 算法[2]对重叠率低的点云数据配准效果不是很好的问题，提出一种新的点云初始配准算法——基于分形维数的全局点云初始配准算法。首先计算点云中各点的维数值；然后根据点云维数分布提取特征点；将特征点使用密度聚类算法进行聚类，用类质心代表每类的属性信息；任意选取三个类质心组成一个三角形，从三角形中寻找全等三角形对，作为匹配点对，进行初始配准；最后将初始配准后的点云数据进行剪枝ICP细配准。该算法对于初始位姿差异大的点云，可以明显缩小点云之间的错位，更加有利于点云细配准，最后获得较好的配准效果。算法流程如图1所示。

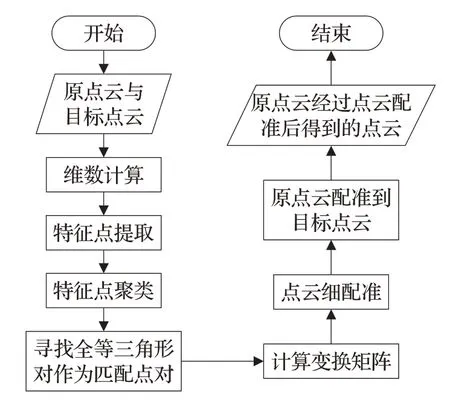
图1 算法流程图

2 点云初始配准

分形几何理论认为，几何体维数可以连续存在，因此常用“相似性维数”来计算和表达具有自相似特征的形状。它可由以下方式来定义：若将一个各边都为单位长度的基本图形G 的各边都割裂为r 个均等的部分，最后能得到由N 个尺度为1 r 的相似于G 的图形，则该图形具有相似性维数logrN 。一维空间中的某长度为m的线段，将它分割为相对尺度标准长度为n 的k 部分时，可以得到k=m/n 个部分，则相似性维数为logk(m/n)=1，等于线段的拓扑维数。任意二维空间中的多边形均可被分割为一系列三角形，使用面积这一参量代替“被分割的子图形”的计数方式时，拓扑维数的数值保持不变；对于两个相似的平面图形，选择图形的最小包围圆的半径作为底，假定其外接圆半径分别为“R”和“r ”，面积分别为“SR”和“Sr”，则其相似性维数为log(R/r)(SR/Sr)=2。同理任意三维空间中，对于两个相似的立体图形，选择图形的最小包围球的半径作为底，假定其外接球半径分别为“R”和“r ”，体积分别为“VR”和“Vr”，则其相似性维数为log(R/r)(VR/Vr)。目前使用维数来定义点云数据的形状属性非常少见。由于Hausdorff维数在很多情形下都很难计算或估计，因而鲜有应用。对于点云数据来说并不需要十分严格的维数定义，只需找到具有维数特性的表达式即可。基于以上分析，将计算Hausdorff维数的思想与表示点云形状属性的需求相关联，得出了点云维数的表达式dim=logrv=logr(dr3)=3+logrd 。其中r 为几何体最小包围球的半径，v 为几何体的体积，d 为比例系数，等号右边第一项“3”为拓扑维数，第二项表示半径为r 的包围球尺度下的形状特征参量[19]。用上述点云维数表达式来定义点云数据中形状的复杂程度。

2.1 点云维数计算

维数值用来表示点云形成的局部表面的粗糙程度，因此用维数可以区分点云数据各点处的不同形状。计算点云维数的算法如算法1所示。

算法1 计算点云维数

输入：点云集合X={x1,x2,…,xi,…,xn}。

输出：点云维数集合Dim={verDim(1),verDim(2),…,verDim(i),…,verDim(n)}，其中verDim(i) 表示第i 个点的维数值。

针对点云X 中的每个点xi做如下操作：

（1）计算xi的k 近邻集合N(xi)，计算N(xi)的最小包围球半径r；

（2）将N(xi)中的对象进行四面体剖分，得到一组四面体集合tr={s1,s2,…,si,…,sm}；

（4）计算点xi的维数值verDim(i)=logrsumV 。

邻域选取方法：k 一般取值为10至50之间；当点云形成的局部表面比较平滑，凹凸变化不明显时，k 取值较大；反之，k 取值较小。

2.2 特征点提取

点云中各点的维数值表示了局部表面的粗糙程度，因此通过维数值可以将点云中的形状特征点提取出来。通过大量实验数据证明，点云数据中的特征主要分布在维数直方图的左右拐点两侧。而维数值大于右侧拐点的部分主要分布的是点云数据的边界特征点，维数值小于左侧拐点的部分主要分布的是点云数据内部的特征点。

如图2所示，点云数据维数分布直方图用棕色和蓝色两部分表示，提取的特征点的维数分布用棕色部分表示。点云数据维数分布直方图中棕色与蓝色交界处的维数值为左侧拐点，左侧拐点处的维数值为临界值DimBound 。点云数据内部形状特征点分布在维数值小于维数分布直方图的左侧拐点处的点。特征点集合featurePoints 表示为：

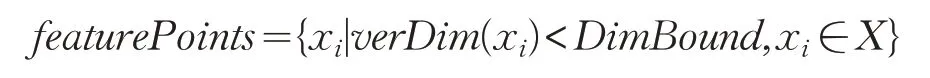
2.3 特征点进行密度聚类

用基于密度聚类算法[20]将提取出的特征点进行聚类。基于密度的聚类算法，通过特征点分布的紧密程度来确定聚类结构。聚类算法参数包含邻域内对象数量最小值MinPts 以及邻域半径Radius。

MinPts 的计算方法：MinPts 的确定依赖于数据集中对象的数量，当数据集中的对象为有限个时，MinPts=integer(m/25)[21]。其中m 是数据集中对象的数量，integer表示取整运算。当数据集中对象很多时，MinPts=20[21]。点云中特征点聚类时，一般设置MinPts=20。

邻域半径Radius 的计算方法：Radius 是依据距离计算得到的。例如一个数据集A(m×n)，即数据集A 中有m 个n 维的数据对象。在与数据集A 相同的数据分布范围内模拟m 个均匀分布的对象，将模拟形成的数据集合记作B。计算B 中每个对象bi的第k 个近邻点与对象bi的欧式距离，此处k=MinPts。接下来将m个距离值从小到大排序，Radius 为距离排序中位于95%[21]位置上对应的距离值。因为此处提取的特征点，相对于一般的聚类数据，类与类之间区分明显，类内数据比较集中，因此需要增设另外一个参数RTimes，表示Radius的倍数值，此处实际的邻域半径为Radius×RTimes。

当特征点分布比较明显、集中时，MinPts 值较大，RTimes(RTimes ∈(0,1])较小；当特征点分布略显分散时，参数值MinPts 较小，另一个参数值RTimes(RTimes ∈(0,1])较大。密度聚类算法如算法2所示。

算法2 密度聚类算法

输入：点云数据集合X={x1,x2,…,xi,…,xn}；邻域参数(RTimes,MinPts)。

输出：类划分，即点云数据聚类后形成的类集合C={c1,c2,…,ci,…,cs},ci表示第i 类。

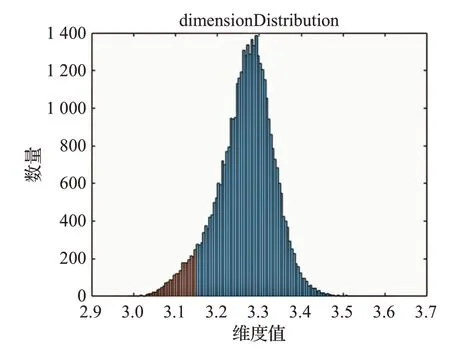
图2 点云维数分布以及特征点维数分布

针对数据集合X 做如下操作：

（1）确定X 中的核心对象集合Ω ：

num(N(xi))＞MinPts

其中，num(N(xi))表示点xi的邻域半径内邻域点的数量。若点xi的邻域半径内邻域点数量大于MinPts，则点xi为核心对象，将点xi加入到核心对象集合Ω 中。

（2）将能够连通[18]的每一组核心对象，以及到核心对象距离小于邻域半径的点都放到一起，形成一个类ci。

（3）针对所有的核心对象进行（2）的操作，得到聚类结果。

2.4 获取匹配点对

进行点云配准，经常采用的几何特征提取方法是将点云中的点邻域拟合为局部二次曲面来获得点云的法向量、高斯曲率等信息作为特征信息[6]。

该算法从点云的全局结构进行初始配准，而不是根据点云的局部信息进行配准。特征点经过密度聚类后，获得每一类的质心，类质心表示点云数据中某一局部位置信息。所有的类质心代表了点云中特征点的全局结构。根据特征点形成的全局结构，寻找相同的结构来获得匹配点对。从原点云类质心集合中任意选取三个类质心对象，构建三角形；从目标点云类质心集合中任选三个对象，构建三角形；通过比较构建的两个三角形是否全等，判断是否具有相同的结构，是否是匹配点对。获取匹配点对的算法如算法3所示。

算法3 获取匹配点对

输入：原点云类质心集合CenterSrc={cs1,cs2,…,csi,…,css}；目标点云类质心集合CenterDst={cd1,cd2,…,cdi,…,cdq}。

输出：三对匹配点对。

（1）通过组合思想从CenterSrc 中任取三个对象，构建出原点云的三角形索引集合IndexSrc={inSrc1,inSrc2,…,inSrci,…}；同理得到目标点云的三角形索引集合IndexDst={inDst1,inDst2,…,inDsti,…}。

（2）构建三角形信息。三角形信息包括顶点坐标、顶点的对边长度；计算三角形索引集合IndexSrc 和IndexDst 中每个三角形的信息，得到原点云三角形集合TrSrc={trSrc1,trSrc2,…,trSrci,…}和目标点云三角形集合TrDst={trDst1,trDst2,…,trDsti,…}。

（3）判断TrSrc 与TrDst 中是否存在全等三角形。三角形全等的判断过程：依次比较三角形trSrci与trDsti中三条对应边的差值比例是否在阈值参数内，满足条件则认为是全等三角形对。

（4）从获得的全等三角形对中选择差值比例和最小的作为最终的全等三角形对，对应的三个顶点为匹配点对。

2.5 计算变换矩阵

由三个三维对应点对求解变换矩阵，变换矩阵包括旋转矩阵R 和平移向量t 。变换矩阵的计算采用直接计算法[22]。计算变换矩阵的算法如算法4所示。将原点云经过估计变换矩阵R 和t 变换后，得到初始配准后的点云数据。

算法4 计算变换矩阵

输入：原点云中的点srcData={p1,p2,p3}，目标点云中的对应点dstData={p11,p22,p33}。其中p1的对应点是p11,p2的对应点是p22,p3的对应点是p33。

输出：旋转矩阵R 和平移向量t。

（1）计算原点云p1、p2、p3构成的三角形的重心q1；计算由p1、p2、p3三点构成的三角形的单位法向量n1；过重心q1，沿着单位法向量n1方向，取长度为1的点p4。

（2）将srcData 所在的坐标原点移动到p4点，得到三点的坐标记作s1、s2、s3。

（3）同理，对目标点云进行上述（1）、（2）操作，将目标点云得到的三点坐标记作t1、t2、t3。

（4）计算旋转矩阵R：

(t1t2t3)=R×(s1s2s3)

R=(t1t2t3)×inv((s1s2s3))

其中inv((s1s2s3))表示矩阵(s1s2s3)的逆矩阵。

（5）计算平移向量t。已知旋转矩阵R 和原点云与目标点云中的任意一对对应点si和ti，则有：

ti=R×si+t

3 点云细配准

完成上述初始配准过程后，得到的点云结果继续采用剪枝ICP[11]细配准算法进行配准，得到最终的点云配准结果。

4 实验结果与分析

实 验 环 境 为Windows7 操 作 系 统，CPU 为Intel®Pentium®CPU G840@2.80 GHz，内存为8 GB。程序使用Matlab编写。为了验证该算法的可行性和有效性，实验采用斯坦福大学计算机图形学实验室获取的bunny、dragon、Armadillo、happyStandRight 点云数据。实验分两种情况进行测试：一种是重叠率高的点云数据模型；另一种是重叠率低的点云数据模型。

4.1 重叠率高的点云数据模型实验

为测试该算法能够对重叠率高的点云数据进行配准，采用重叠率在90%左右的点云数据进行测试。

实验采用斯坦福大学计算机图形学实验室获取的bunny000、bunny045 点云数据，点云数据的维数分布直方图、特征点、特征点聚类结果以及配准结果等具体实验过程如图3所示。

图3：（a）中蓝色与棕色两部分是bunny000 点云数据的维数分布直方图，直方图中棕色部分为bunny000中特征点的维数分布；（b）为bunny000 提取的特征点，其中红色为bunny000 点云数据，绿色为bunny000 中提取的特征点；（c）为bunny000 特征点聚类结果，聚类结果为8类，类与类之间用空间距离和颜色进行区别，其中每一类的类质心用黑色的实心点表示；（d）为bunny045维数分布直方图；（e）为bunny045特征点提取结果；（f）为bunny045 特征点聚类结果，聚类结果为12 类；（g）为bunny000 与bunny045 的初始位姿；（h）为bunny000 与bunny045 的初始配准结果；（i）为bunny000 与bunny045的细配准结果。

按照上述实验过程，同时对ArmadilloBack_120、ArmadilloBack_150，dragonStandRight_0、dragonStandRight_24，ArmadilloBack_0、ArmadilloBack_30 点云数据进行实验，实验结果如图4、图5、图6所示。上述点云数据的配准性能如表1所示。

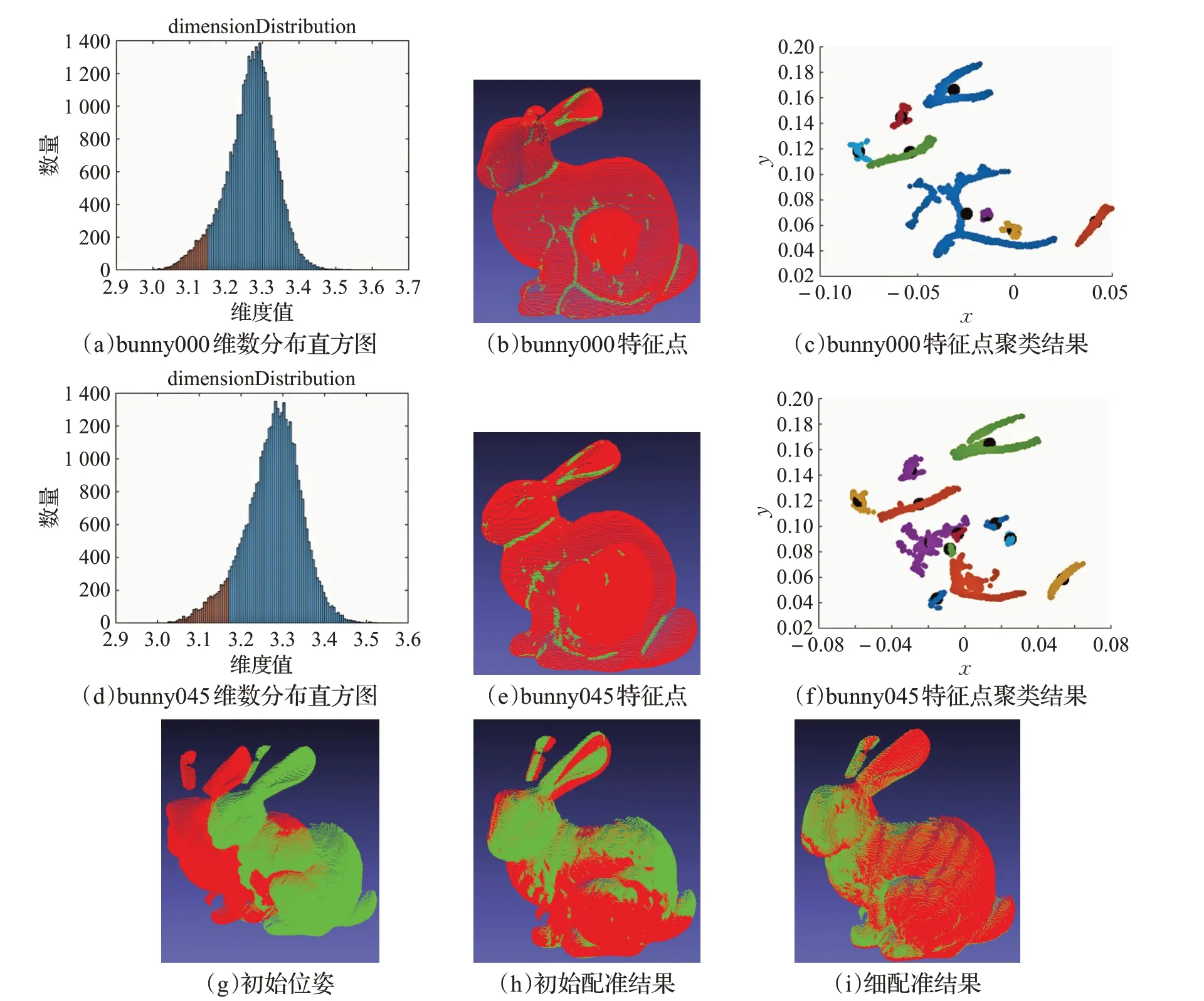
图3 bunny000与bunny045维数分布、特征点聚类以及配准结果

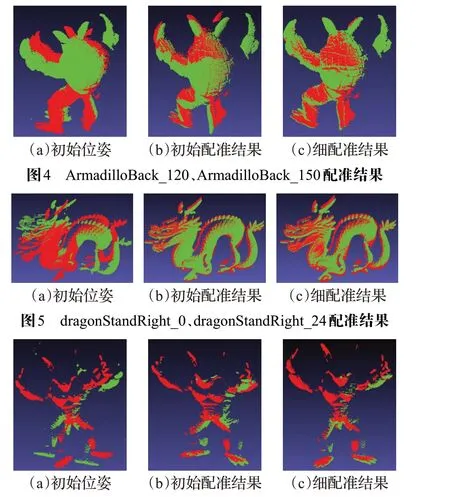
图6 ArmadilloBack_0、ArmadilloBack_30配准结果

由图中的实验结果可以证明，对于重叠率较高的点云数据，本文提出的算法具有良好的配准效果。配准时间与维数计算和由组合算法形成的三角形个数有关。由于聚类后的类数量有限，因此配准时间主要用于维数计算。影响维数计算有两个因素：点云模型中的点数量以及维数计算时k 近邻值的选择。当点云中点数量相同时，k 值越小，维数计算时间越短；k 值越大，维数计算时间越长。bunny000与bunny045点云形成的局部表面比较平滑，凹凸变化不太明显，k 取值较大；dragon-StandRight_0与dragonStandRight_24点云形成的局部表面凹凸变化比较明显，k 取值较小。因此当点数量比较接近时，bunny000 与bunny045 的配准时间比dragon-StandRight_0与dragonStandRight_24的配准时间长。

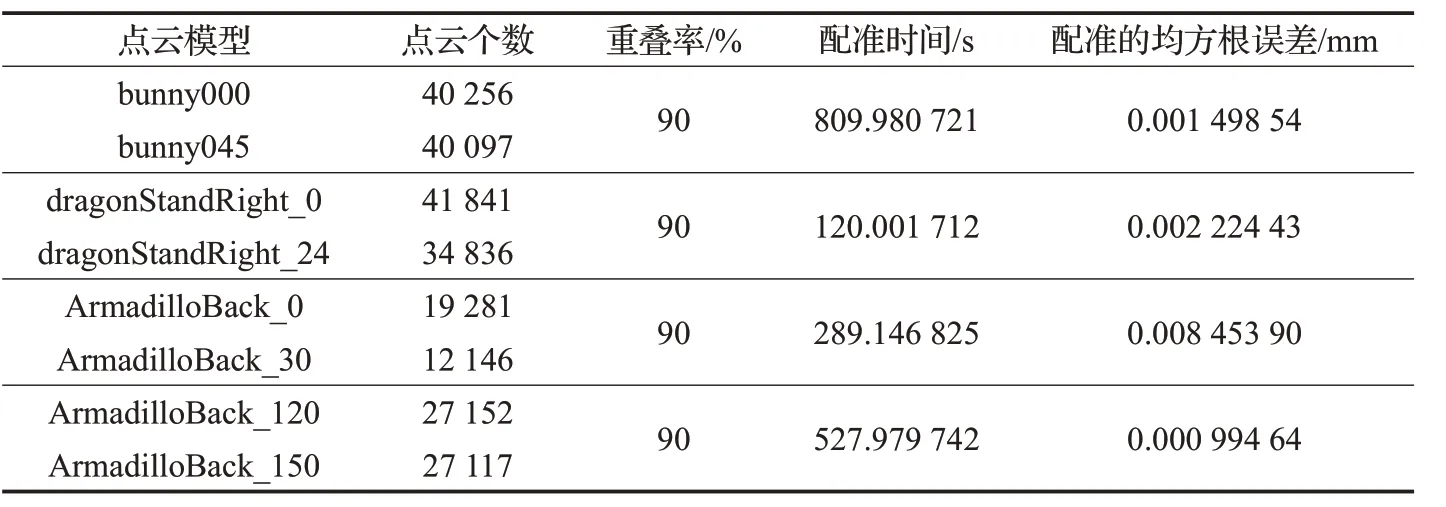
表1 重叠率高的点云模型的配准性能

4.2 重叠率低的点云数据模型实验

经过大量实验证明，当点云数据之间的重叠率低于45%时，点云数据之间的相同结构存在的可能性较低。因此该算法适用重叠率约在45%以上的点云数据之间的配准。

实验结果展示部分选取了几个具有代表性的较为复杂的点云数据模型，这些点云模型之间的重叠率约为45%。斯坦福大学计算机图形学实验室获取的bunny045、bunny090 点云数据，对应的角度分别为45°、90°；ArmadilloOnHeadMultiple_180、ArmadilloOnHeadMultiple_270点云数据（简记为Armadillo_180、Armadillo_270），对应的角度分别为180°、270°；happyStandRight_48、happyStandRight_96点云数据（简记为happy_48、happy_96），对应的角度分别为48°、96°。

图7 bunny045、bunny090点云数据配准结果

同时该算法的初始配准结果与另两种算法分别进行了对比：一种是通过多尺度邻域信息来获得对应中心点的一组法向量信息，通过法向量等信息作为快速描述符（fastDesp）进行初始配准[6]。由于文献[6]算法的细配准也是采用剪枝ICP[11]算法，与本文算法的细配准过程相同，因此将本文算法的初始配准结果与fastDesp 的初始配准算法结果进行对比。另一种算法是Go-ICP算法[2]。

实验结果如图7、图8、图9所示。各实验结果图中（b）是本文算法初始配准结果，（c）是本文算法细配准结果，（d）是采用fastDesp[6]算法进行初始配准的结果，（e）是Go-ICP[2]算法配准结果。三组点云数据的配准性能如表2所示。

bunny045 与bunny090 的配准结果：图7（a）中第一行绿色图表示bunny045 的初始位姿，点云角度为45°，红色图表示bunny090的初始位姿，点云角度为90°，两片点云数据的重叠率大约为45%，第二行的图为bunny045与bunny090 在一个坐标系下的初始位姿；图7（b）中兔子耳朵的对应位置大致正确，图7（b）本文算法初始配准后的位姿差异明显小于图7（d）初始配准算法[2]和图7（e）Go-ICP算法[6]的位姿差异。

图8 Armadillo_180、Armadillo_270点云数据配准结果

Armadillo_180与Armadillo_270的配准结果：图8（a）中第一行绿色图表示Armadillo_270 的初始位姿，点云角度为270°，红色图表示Armadillo_180的初始位姿，点云角度为180°，两片点云的重叠率大约为45%，第二行为Armadillo_180与Armadillo_270在一个坐标系下的初始位姿；图8（b）本文算法初始配准结果明显优于图8（e）Go-ICP算法[6]的配准结果，但是由于k 值的选取不够精确，Armadillo_180 与Armadillo_270 特征点的选取不够精确，会存在少部分的遗漏，对应点对会存在误差，配准结果存在上下的错位，因此本文算法的初始配准效果没有图8（d）初始配准算法[2]效果好。

图9 happy_48、happy_96点云数据配准结果

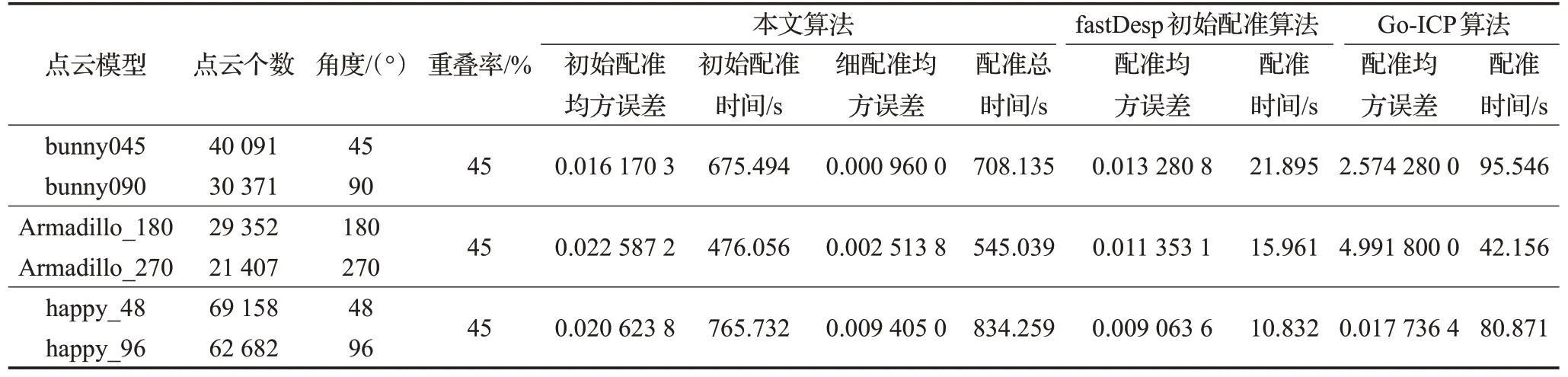
表2 重叠率低的点云模型配准性能

happy_48 与happy_96 的配准结果：图9（a）中第一行绿色图表示happy_48 的初始位姿，点云角度为48°，红色图表示happy_96的初始位姿，点云角度为96°，两片点云的重叠率约为45%，第二行为happy_48与happy_96在一个坐标系下的初始位姿；图9（b）初始配准结果中happy_48与happy_96的头部上方部位之间的角度差异明显变小，位置上存在上下之间的错位，但对应大致是正确的，同时happy_48 与happy_96 的身体侧面部位之间的对应大致是正确的；图9（d）与图9（e）两种算法的配准结果中happy_48与happy_96的头部上方部位仍然存在很大的角度差异，同时身体侧面部位也存在很大的角度差异，能明显看出图9（b）的配准结果优于图9（d）和图9（e）的配准结果。

通过上述三组对比实验，可以得出本文算法的初始配准结果能够明显缩小点云之间的位姿差异。

同时观察上述实验中图7、图8、图9 中各自对应的图（c）本文算法的细配准结果，可以得出本文算法对于角度差异大、重叠率低的点云数据能够达到较好的配准效果。

均方误差的衡量标准是计算两片点云中每对对应点之间距离的平方和的均值。然而均方误差中的对应点是将一片点云中的点与另一片点云中距离最近的点作为对应点来进行选择的。事实上，这种判断对应点的标准并不合理，尤其是针对bunny和happy这两组实验，当点云重叠率低时真正的对应点对数量较少，按照均方误差中对应点的选取标准会造成均方误差值较大。例如happy_48 与happy_96 中，本文算法的细配准结果明显优于初始配准算法[2]的配准结果，但是比较各自对应的均方误差发现，本文算法的细配准结果的均方误差大于初始配准算法[2]的均方误差。因此只用均方误差来衡量配准效果是不太合理的。表2 中本文算法比另外两种算法配准时间长，还需改进提高。

本文算法根据分形维数属性提取点云数据内部的特征点，将这些特征点进行聚类后，得到特征点之间的相对位置分布，通过三角形这种简单结构信息来寻找两片点云中相同的相对位置分布，完成初始配准。上述的实验结果可以证明，对于重叠率45%以上，角度差异在45°范围内的点云数据之间的配准，基于分形维数的全局点云初始配准算法能够有效缩小点云之间的位姿差异，更加有利于点云细配准。

5 结束语

基于分形维数的全局点云初始配准算法，将二维中的分形维数用于三维点云中进行特征提取，不同于之前的曲率、法向量等点云特征提取方法；没有采用点云的局部特征信息进行配准，从点云全局结构进行配准。本文算法能够对初始位姿小的点云数据进行有效配准，同时对于初始位姿差异较大的点云数据，可以有效缩小点云之间的位姿差异，缩小点云之间的错位，达到较好的配准效果。

但是，本文算法也存在一定的缺陷：适用于点云局部表面有凹凸的情况，当点云中存在大量平面时，此算法不适用。由于使用的是k 近邻计算维数，维数计算所需时间较长。同时k 值的精确选取需要进一步研究。