培养学生良好审题习惯的途径

【摘要】本文论述培养学生良好审题习惯的策略，提出在概念教学中紧扣重点，透彻理解;在计算教学中认清字符，捋顺程序;在解决问题中把握全局，重视细节等教学建议，进一步培养学生良好的审题习惯。

【关键词】小学数学 概念教学 审题习惯 审题方法 认知偏差

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2020）45-0132-02

一个偶然的机会，笔者看到一张小学数学单元测试卷上的一道题令人印象深刻：马丽、陈杰和赵光进行1分钟踢毽子比赛，马丽踢了120个，陈杰踢的个数是马丽的[58]，赵光踢的个数是马丽的[43]。赵光1分钟踢了多少个毽子？经调查发现，全班39人中有18人出现这样或那样的错误，其中有13人列出的算式雷同：120×[58]×[43]。如果将13名学生的低级错误归咎于学生受思维定式的“胁迫”，即受刚刚学过的分数连乘应用题的定式影响，倒不如说是学生没有认真审题，导致在提取和处理数学信息时产生错解。由此可见，良好的仔细审题习惯具有极其重要的作用，审题时麻痹大意、态度怠慢，必然造成解题出错。下面笔者结合自身的教学实践，分析如何在数学教学中有效培养学生的审题能力，使学生渐渐养成认真审题的好习惯。

一、概念教学：扣住重点，透彻理解

在小学数学教学中，基本概念是构建数学知识的基石，是正确理解和掌握其他数学法则、性质、定理、规律、公式等数学结论的必备工具，是解决数学应用题的“常规武器”。在概念教学中，要想将概念的内涵和外延揭示透彻，就要牢牢抓住知识要点和核心，避免概念负迁移的发生和扩散。

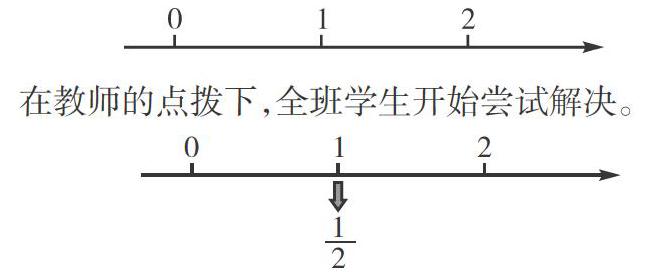
例如，在教学《分数的意义》后，教师出示练习：请在下面这条数轴上找到分数[12]的坐标。

在教师的点拨下，全班学生开始尝试解决。

有少数学生得出这样的结果（如上图），而且还振振有词：把整个线段视为单位“1”，等分成2段，其中1段用分数表示就是“[12]”，因此，這一段的末端的端点就是分数“[12]”的坐标。这样的结论令人惊诧，学生为什么会这样思考呢？深入分析这背后的成因，笔者发现，学生初遇“一个物体、一个整体、一个计量单位”后，教师就不由分说地勒令学生接受它们为单位“1”这个观念，把一个物品视为整体，但是让学生在思想上把一个整体、一个计量单位视为单位“1”，则有些强人所难，因为此时的学生对一个整体和一个计量单位的认识本身就模棱两可，再直接跳级去抽象成单位“1”，步子有些大。

部分学生误把这条两个长度单位的“线段”看作单位“1”，单位“1”找错了，后面出错是肯定的。这是由于学生审题不严造成的结果，题目说找到分数[12]的坐标，此时分数[12]就是一个数值，是除法意义下的商值，就是1÷2=0.5，等同于0.5，而不是分数基本意义下的比例。因此，在概念教学中，教师要把准概念的内涵和外延，明确概念定义时的所有定义项，也就是前提条件和限制条件，领会其本质，教会学生审题时切中关键词眼。本题的关键词眼就是分数[12]，而不是线段的[12]，在指导学生完成这道习题时，教师先引导学生将分数[12]化成小数0.5，然后在数轴上的0和1之间取其中点，这个点就是[12]的坐标。同样的，要求学生在数轴上标出假分数的坐标时，教师要引导学生先将假分数化成带分数，即整数部分加上一个真分数。整数部分直接在数轴上找到该点，真分数则可以先化成小数，然后在数轴上找到其对应的点即可。

二、计算教学：认清字符，捋顺程序

计算在小学数学教学中地位特殊，是小学数学内容的“压舱石”和“定盘星”，是学生构筑数学大厦的“钢筋水泥”。小学生在计算中丢分是常事，许多压轴题和得分题都栽在计算上，教师应帮助学生分析错因，从审题上切断错误的源头，防微杜渐，提高警惕，最大程度减少错误的发生，提高教学效率。

学生对数字、符号感知迟钝，对数据的感知缺乏敏锐性和连贯性，易把数字、符号看错写错，是计算出错的头号杀手。如有些学生时常将8.56抄写成8.65，把“÷”写成“+”、把“+”写成“×”，等等。学生在运算过程中，受到简算的负迁移，将一些凑整数对强迫性地组合，而不顾运算定律和运算性质，出错是必然的。

例如在计算55+45÷5时，由于55与45相加正好是100，容易计算，因此，不少学生由于本能上的“趋利避害”，想当然地做出有利于计算的决定，不顾先算除法再算加法的计算法则，将算式算成55+45÷5=100÷5=20。又如计算9000÷4×25，学生受乘法结合律的影响，会出现这样的计算：9000÷4×25=9000÷（4×25）=9000÷100=90。由此不难推想，学生运算[38]+[58]×[48]、[95]-[23]+[13]时出现差错也是情有可原。另外，学生学习了一些运算律后，往往凭经验和直觉自创一些定律，但由于经验的单薄和直觉的稚拙，再加上没有深厚的数学理论基础导致频频出错，例如，在学习乘法分配律a×（b+c）=a×b+a×c后，学生就会仿造出一个山寨版的“除法分配律”a÷（b+c）=a÷b+a÷c，这样得到的式子虽有分配律的外形，却没有实际内蕴。在教学这类型算式时，教师要引导学生根据混合运算的顺序来计算。同时，还要从学生的非智力因素着手，排除思维定式的干扰，培养学生仔细审题、书写端正、检查验算的良好习惯。

三、问题解决：把控全局，重视细节

小学数学问题解决考验学生分析处理问题的能力和决策筹划的能力，是将数学应用于生活的具体体现。解决问题类内容难教、难学似乎成了师生之间的共识，教师要引导学生从审题入手，抓住重点、注重细节、把握整体，最大限度地降低错误发生几率，尽可能阻断错误发生的源头。

如“一块花圃有[67]公顷，种牡丹用去[27]，种紫罗兰用去[37]，还剩下几分之几？”对于这道题，有将近一半的学生这样列式：[67]-[27]-[37]。究其原因，学生对单位“1”认识不足，印象不深，并受“[67]”这个数据的迷惑和干扰，而自动忽略单位“1”的默认存在，出现这样的错误同样也存在审题粗心大意的情况，草草列式解答，导致出错。

又如在解决一些圆锥的体积问题时，学生把心思放在寻找圆柱体的底面积和高上，尤其是底面的半径没有直接告知的时候，大费周章将对应圆柱体的体积求出来，一时兴奋，忘了题目要求的是圆锥体的体积，也就是说很容易把公式中的“[13]”弄丢;同样的，在解决一些制作容器需要多少铁皮（也就是求容器的表面积时），不注意题后的要求（如得数保留整数或者两位小数等），“无盖”“一对”等细节也容易被忽视。

针对学生出现的这种非智力因素造成的错误，教师在解决问题教学中，要全面考虑，从各个方面训练学生的审题能力，通过设计条件不足、条件过剩以及条件杂乱等问题，训练学生的辨别力和判断力。比如第一道题，题中的信息是花圃面积为[67]公顷，而不是单位“1”的[67]，如果直接用[67]去减后面的分数，出错也就再正常不过了。同样，第二题求圆锥的体积出错则是忘记圆锥的体积是等底等高的圆柱体积的[13]，这是学生审题不清的结果。所以，教师要引导学生用心分析题目涉及的各种数量关系，加强对有用的数学信息的筛选，并注意看清一些细节和关键性字眼，制订最优方案，一边解题一边检验，步步为营，环环相扣，从而顺利解决问题。

总之，教师在数学教学中应立足长远，教会学生科学的审题方法，培养学生良好的审题习惯，使学生每次解题时都能自觉地按照这种习惯行事，不断提高自身的审题能力。

作者简介：唐耕（1974— ），女，广西玉林人，大学本科学历，一级教师，主要研究方向为小学数学教学。

（责编 林 剑）