基于Matlab的IRB2400机器人轨迹规划及运动学分析

孙增光，王士军，孟令军，王春璐，周永鑫

(山东理工大学 机械工程学院, 山东 淄博 255049)

六自由度关节机器人动作灵活性高、工作空间范围大，并且结构紧凑、占地面积小，能够解放劳动力，提高劳动效率。因此，在机床上下料、喷涂、弧焊等机械制造业中得到了广泛应用[1]。

利用Matlab对IRB2400机器人建模仿真，可以直观了解机器人工作形态。为了提高机器人运动轨迹精度和稳定性，对机器人进行轨迹规划[2]。通过运动学分析，确定机器人末端执行器的位姿[3]，并进行机器人正逆运动学求解，以验证机器人模型的正确性。运动学分析是机器人控制的基础，本文对IRB2400机器人进行轨迹规划和运动学分析，以期为离线编程提供有效的验证手段[4]。

1 机器人模型的建立

1.1 ABB IRB2400机器人

IRB2400是全球应用最广的工业机器人，该机器人坚固耐用、可靠性强、维护间隔时间长，具有最佳的轨迹精度和重复定位精度, 零件生产质量稳定，它的有效载荷大，到达距离远，适用范围广[5]。IRB2400机器人空间结构图如图1所示。

图1 IRB2400空间结构图

1.2 机器人DH坐标系的建立

在进行运动学分析时，首先根据建立的机器人连杆坐标系，建立各连杆之间的关系，最终推导出机器人末端相对于机器人底座的位姿变换。对于转动关节构成的机器人来说只有关节角θi为变量，其他3个参数由机械结构决定。连杆i相对于连杆i-1的变换矩阵表示为

坐标系n相对于坐标系0的变换矩阵为

可以看出,要求变换矩阵需要知道连杆长度ai-1、连杆转角αi-1、连杆偏距di和关节角θi4个参数。运用DH参数法建立的ABB IRB2400机器人连杆坐标系如图2所示。

图2 机器人连杆坐标系

根据建立的连杆坐标系求出连杆各参数，建立的DH参数表见表1。

表1 机器人DH参数表Tab.1 Robot DH parameter table

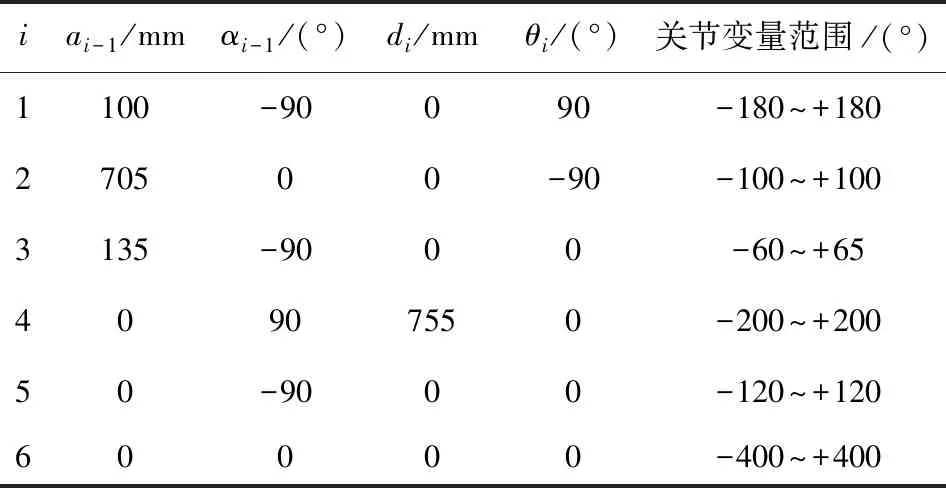
iai-1/mmαi-1/(°)di/mmθi/(°)关节变量范围/(°)1100-90090-180～+180270500-90-100～+1003135-9000-60～+6540907550-200～+20050-9000-120～+12060000-400～+400

1.3 Matlab仿真机器人

利用Matlab建立机器人仿真模型，部分代码如下：

L1=Link([pi/2 0 0.1 -pi/2 0]);

L2=Link([-pi/2 0 0.705 0 0]);

L3=Link([0 0 0.135 -pi/2 0]);

L4=Link([0 0.755 0 pi/2 0]);

L5=Link([0 0 0 -pi/2 0]);

L6=Link([0 0 0 0 0]);

robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','ABB IRB 2400');

输出机器人模型时，定义关节角姿态为0，并通过teach()指令查看所建立的机器人，通过拖动关节角调节滑块来改变关节角度值，使机器人呈现出不同的姿态。生成的机器人仿真模型如图3所示。

图3 机器人仿真模型

2 关节空间轨迹规划

进行轨迹规划可以使机器人运动变平稳，减少振动和冲击，同时也能避免消耗额外能量并减少机械部件磨损[6]。关节空间轨迹规划的基本思路是使用逆运动学计算方法，将笛卡尔空间中的路径点转换成对应的关节角，然后使用插值点计算方法，对关节型机器人的各个关节计算插值点，使关节型机器人的各个关节同步且顺滑地到达目标点[7]。

2.1 三次多项式插值算法的轨迹规划

关节空间多项式轨迹规划从三次多项式开始，在轨迹规划中，把机器人的关节角度变换成与时间有关的函数，然后对角速度和角加速度进行约束。

假设初始时刻t0的角度是θ0，在终点时刻tf的角度是θf，为使运行平稳，给定4个约束条件，起始点和终止点关节角度为

(1)

起始点和终止点关节角速度为

(2)

由此确定了三次多项式关节插值函数为

θ(t)=a0+a1t+a2t2+a3t3

(3)

确定关节角速度及角加速度为

(4)

将约束条件(1)和(2)代入到函数关系式(3)和(4)中，得到a0、a1、a2和a3相关的线性方程为

(5)

求解以上方程组得

(6)

指定起止位置q_array=[0,50,150,100,40]，指定起止时间t_array=[0,5,10,15,20]，指定起止速度v_array= [0,10, 20,-15,0]。用Matlab计算三次多项式插值，得到的关节角度、角速度和角加速度随时间变化的曲线如图4所示。

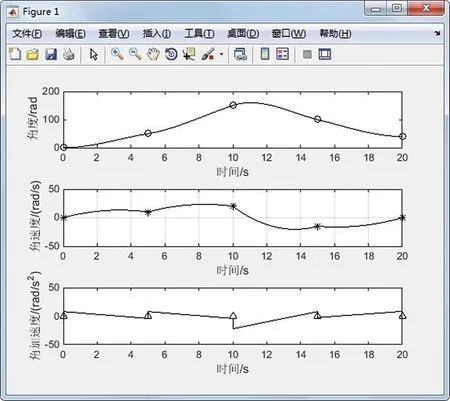
图4 三次多项式轨迹规划

通过分析三次多项式的关节空间轨迹规划图可以看出，机器人运动关节角度、角速度是连续性的，但由于没有对关节角的加速度约束，因此关节角的加速度有突变，机器人运动不稳定，会导致机械系统产生一定的冲击。

2.2 五次多项式插值算法的轨迹规划

由于机器人在实际工作中对工作路径有更高的要求，三次多项式插值算法难以满足，所以提出了五次多项式插值算法。它不仅对路径的起点与终点的角度、角速度进行约束，也对角加速度有规定，需满足6个约束条件，其函数表达式如下：

相应的五次多项式描述规划轨迹为

θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5(8)

通过求解方程组得

(9)

指定和三次多项式同样的起止位置、时间、速度，指定起止加速度a_array=[0,20,30,-20,0]，用Matlab计算五次多项式插值，得到的关节角度、角速度和角加速度随时间变化的曲线如图5所示。

图5 五次多项式轨迹规划

由图5可以看出，五次多项式插值得到的加速度平滑，能保证关节角度、角速度和角加速度的连续性，使关节运动平稳，避免了冲击和振动。

比较两种插值方法可以看出，三次多项式的加速度发生突变，这对机器人的关节电动机冲击较大，而五次多项式的加速度较为平滑，没有突变。因此，五次多项式的插值比三次多项式更为精准。

3 机器人运动学分析

机器人运动学研究是在不考虑受力的情况下机器人的运动特性，主要包括机器人的位置、速度和加速度等内容[8]。

给定机器人末端初始关节角度qA= [0 0 0 0 0 0 ]，机器人末端终止关节角度qAB=[0 -pi/4 -pi/4 0 pi/8 0]，规定采样时间间隔为0.01 s，采样时间为10 s。用Matlab进行仿真，得到机器人末端轨迹图如图6所示，末端位移图如图7所示。

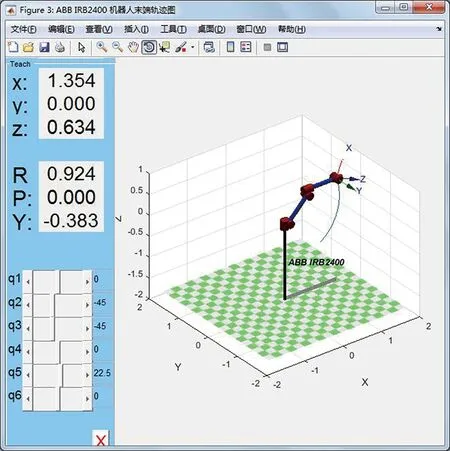
图6 机器人末端轨迹图

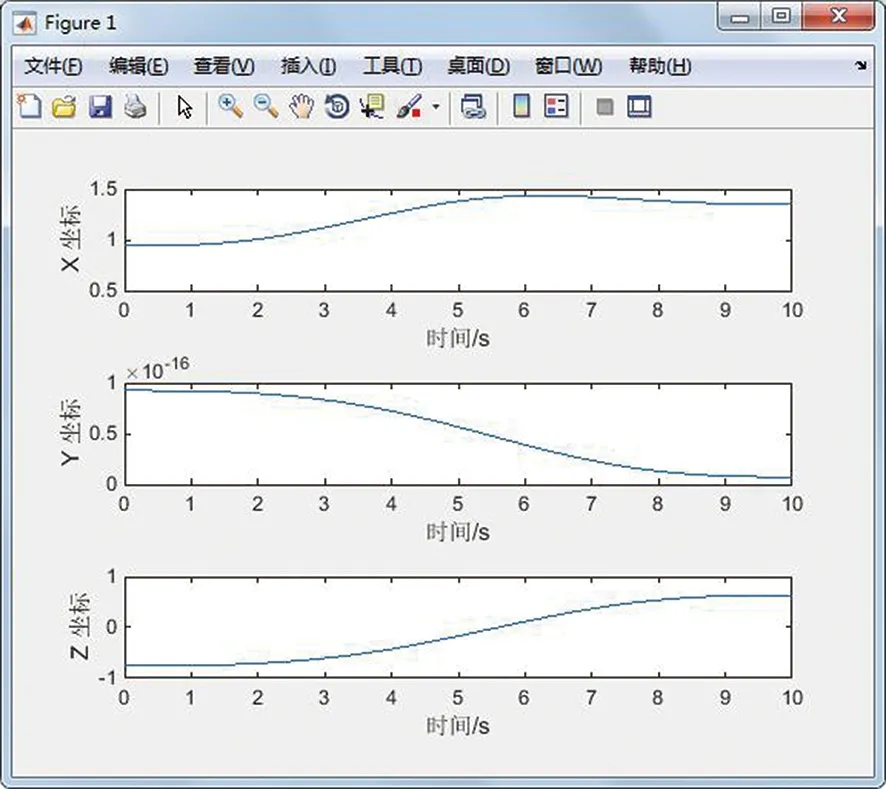
图7 机器人末端位移图

为了更好地了解机器人的各关节运动情况，利用Matlab求出了各关节的运动曲线(如图8所示)、角速度曲线(如图9所示)和角加速度曲线(如图10所示)。

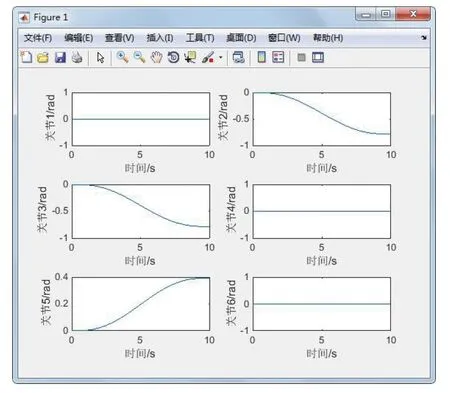
图8 各关节的运动曲线

图9 各关节的角速度曲线

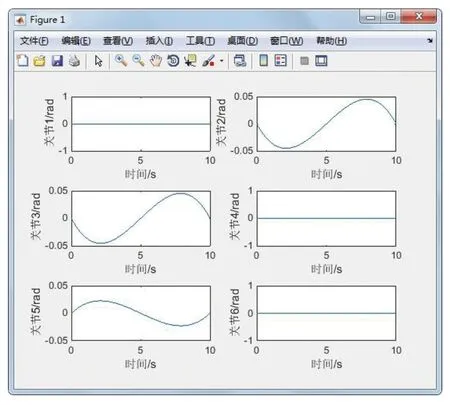
图10 各关节的角加速度曲线

从图8—图10可以看出，得到的各曲线均光滑连续，得到的各关节最大角度、最大角速度、最大角加速度差别不大。在0～5 s时间段内角速度逐渐增加，在5～10 s时间段内角速度逐渐减少，终点处角速度和角加速度最终为0，说明机械臂是一个先加速后减速的过程。从角速度和角加速度曲线可以看出，各曲线平稳无振动，各关节性能良好。

4 正运动学与逆运动学

正运动学是根据给定的各关节角度变量计算机器人末端的位置和姿态。而逆运动学是根据末端已知的位置和姿态计算机器人的关节角，其关系如图11所示。

图11 正运动学和逆运动学关系

4.1 机器人正运动学求解

假设机器人初始关节角qA=[0 0 0 0 0 0 ]，在Matlab中通过fkine函数计算相应的变换矩阵，得到机器人初始位置的末端齐次变换矩阵为

假设机器人终止位置时的关节角qB=[0 -pi/4 -pi/4 0 pi/8 0]，计算得终止位置的变换矩阵为

4.2 机器人逆运动学求解

在Matlab中，利用Robotics Toolbox中的ikine函数实现运动学逆问题的求解，以运动学正解后的矩阵TB求解运动学逆问题的关节角。令qi=robot.ikine(TB,'pinv')，求出qi = [0 -0.7854 -0.7854 0 0.3927 0]。

发现qi和qB的值看上去不相等，这时对关节角变量qi使用fkine指令求解对应的变换矩阵为

可以发现，qi求解后其对应的变换矩阵Ti与给定的终止位置关节角qB所求的变换矩阵相同，即为同一变换，说明机器人的参数设计和Matlab中构建的仿真模型是正确的。

5 结束语

通过DH参数法求解机器人各参数，利用Matlab teach()指令建立了ABB IRB2400机器人仿真模型，通过改变关节角度值，使机器人呈现出不同的姿态，从而能更加准确方便地了解机器人工作空间和范围。对关节空间轨迹进行了规划，通过分析位移、速度和加速度曲线可知，五次多项式插值算法的加速度平滑，减少了振动冲击，提高了机器人的稳定性。对机器人正运动学和逆运动学进行求解，得到的变换矩阵结果是一致的，说明机器人的参数设计和Matlab中构建的仿真模型是正确的。通过运用Matlab的运动学仿真功能，能方便准确地判断机器人在空间的位置和姿态，这对工业机器人的实际应用具有重要意义。