环锭数码纱Kubelka-Munk双常数配色模型构建及其色彩预测

张婷婷， 薛 元， 贺玉东， 刘曰兴， 张国清

(1. 生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122；2. 愉悦家纺有限公司， 山东 滨州 256623)

环锭数码纺纱系统是数码纺纱技术与环锭纺纱技术相互结合的产物，是一种能对粗纱喂入比例及成纱线密度进行实时在线控制的新型纺纱方法[1-2]。环锭数码纺可纺制以3种颜色为基础的任意混纺比例组合的混色纱。这种新型混色纱的颜色效果是通过多束色纤维须条在纱条中螺旋平行空间排列形成的[3]，其颜色的形成方式既不是单一的光线加法混和，也不是色料的减法混合，而是基于一定面积内同时存在多种色纤维形成的空间混合。混色纱颜色表达的复杂性使得如何准确快速地进行纱线配色成为色纺纱产品开发的关键环节[4]。为此提出将计算机测配色与环锭数码纺技术结合，使得测配色与纺纱在同一工序中完成，进一步缩短工艺流程，提高生产效益。

本文以Kubelka-Munk双常数理论[5]为模型进行环锭数码混色纱的测配色研究，选用品红、黄、青、黑、白5种颜色粗纱为原料，纺制90种不同颜色、不同混纺比的混色纱和5种基色的单色纱，并织成织物，测定其色度参数与不同波长下的反射率；选用相对值法[6]处理Kubelka-Munk双常数理论，对环锭数码纺混色纱的测配色模型进行构建，并对配色算法进行预测效果分析，发现此模型预测效果优良，适用于环锭数码纺混色纱的配比预测。

1 实 验

1.1 样品的制备

1.1.1 环锭数码纺混色纱的制备

实验原料采用规格为4.2 g/(10 m)的品红、黄、青、黑、白5种颜色的粗纱；细纱设计为线密度19.4 tex、捻系数340的Z捻向混色纱；纺纱设备为JWF1551型环锭数码细纱机。将5种不同颜色的粗纱两两相互组合，可得到10种颜色组合模式，如表1所示。以10%为梯度(共9种混纺比)制备90种混色纱，并且用相同的纺纱工艺将5种单色纱制备完成。

表1 双通道粗纱颜色组合模式Tab.1 Dual channel roving color combination mode

设粗纱定重为ρ，混色纱线密度为Tt，前区牵伸比为Eq；混纺比为α1的粗纱通道为主牵伸通道(α1≥50%)，其总牵伸比为E1，后区牵伸比为Eh1；混纺比α2的粗纱通道为辅牵伸通道(α2<50%)，其总牵伸比为E2，后区牵伸比为Eh2。双通道牵伸比计算公式为：

(1)

(2)

(3)

(4)

1.1.2 环锭数码纺混色纱织物的制备

将纺制的95种纱线用16 G宏成HC21K型纬编圆机织造成平针织物。针织物主要规格如下：线圈长度为0.6 mm；横密为53纵行/(5 cm)；纵密为90横列/(5 cm)。 图1示出部分针织实物图。

1.2 样品的颜色测试

将织造的95种针织物用Datacolor 650分光光度计进行颜色测试。实验环境为D65光源、10°标准观察者、30 mm测试孔径，其中光源波长范围取380～700 nm，以10 nm为间隔取样。每种比例取12块针织物样布为测试对象，每块样布任选36个部位进行反射率及色度参数测试，取其平均值分析讨论。表2示出5种基础单色纱线织物色度参数值；表3示出青黑两色粗纱在混纺比为5∶5时纺制的织物在不同波长下的反射率。

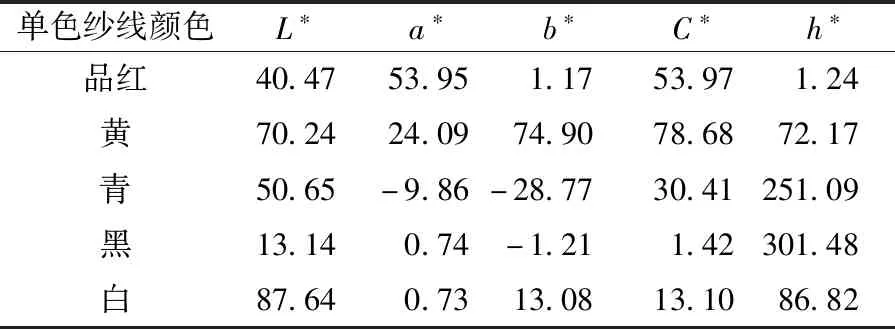
表2 单色纱线织物色度参数Tab.2 Monochrome yarn fabric colorimetric parameters

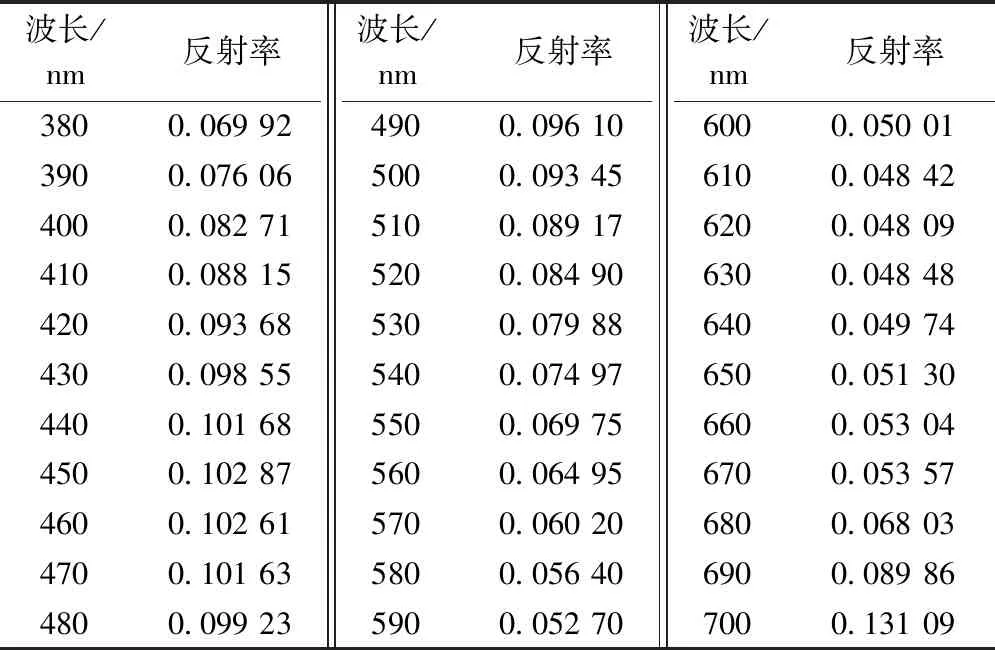
表3 不同波长下的反射率Tab.3 Reflectance at different wavelengths

2 配色模型构建

Kubelka-Munk理论表达式如下。

(5)

式中：K、S分别为被测物体的吸收系数和散射系数；ρ∞为厚度无穷大时的反射率因数。

由于Kubelka-Munk理论是建立在一系列的假定条件基础上[7]，且只涉及反射率、吸收系数和散射系数，一定程度上限制了其应用范围，因此在假定染料分子溶解于纤维，忽略染料浓度的同时，根据K/S的加和性，建立了Kubelka-Munk双常数理论，表达式如下。

(6)

式中：c1、c2、…、cn为染料比例(在纤维混合时指各组分混合比例)；K1、K2、…、Kn和S1、S2、…、Sn分别为不同染料(色纤维)的吸收系数和散射系数，Kt和St分别为基质的吸收系数和散射系数。

Kubelka-Munk双常数理论中，混色样拟合反射率的计算如式(7)所示，由混色样的反射率R计算出K/S值，进而求解得出各单色纤维的吸收系数K和散射系数S，并根据求出的参数K、S计算得到混色样每个波长下的拟合K/S值，从而得到混色样的光谱反射率，通过CMC(2∶1)色差公式计算来表征二者的拟合程度。对于吸收系数K和散射系数S的求解，本文通过相对值法进行计算，并对其拟合程度进行比较。

(7)

式中：(K/S)λ为一定波长λ下的K/S值；R为特定波长下的反射率，%；(K/S)m为混色样的K/S值。

2.1 相对值法

Kubelka-Munk双常数理论中，对于2种色纤维混合来说，存在以下函数关系：

(8)

式中：C1+C2=1，C1和C2为混色样的混纺比，(K/S)m为双混色样的K/S值，(K/S)1、(K/S)2分别为2种单色纤维的K/S值。

联立方程组可得：

(9)

K1=(K/S)1×S1

(10)

通过上述求解吸收系数K和散射系数S时，假定其中一种纤维各个波长下的散射系数均为1，这里不妨设S2=1，根据单色纤维反射率计算得出K/S值，进而得出K2，同时相应求出另一种单色纤维的吸收系数K1和散射系数S1，波长范围同样取380到700 nm，取样间隔为10 nm，但这种方法计算的K值和S值仅仅是2种颜色纤维组合在一起相对产生的，是相互依附的，并非单色纤维本身固有的K值和S值，并不能直观表征色纤维的颜色。

同时为避免上述取样比例及比例组合的影响，本文单色纤维K值和S值的测定同样采用9组混色样构建方程组，设定黑色纤维各个波长下的散射系数均为1，计算各色纤维各个波长下的K值和S值，取均值，如图2、3所示。

由于相对值法建立的基础是假定某一种纯色纤维每个波长的散射系数S全部为1，那么所计算得到纯色纤维的K/S值则与实际测得的是完全相同的，也就是说拟合纯色纤维的反射率与实际测得的反射率也是一致的，故本部分在上述各单色纤维K值和S值求解的基础上，直接选取部分混色样本的反射率预测曲线和实测曲线如图3所示，选取样本与上述相同。

从上图反射率的拟合效果可以看出，拟合的混色样反射率曲线与实测反射率曲线能够实现较好的吻合。在此基础上，计算出所有预测样与混色样的色差,表4示出10种颜色组合5个混纺比的拟合色差。

通过分析可以发现，由相对值法计算吸收系数K和散射系数S所得到的不同颜色组合预测样和混色样的拟合色差大部分均在可接受范围内，表明所建立的颜色预测模型实用性优良，为建立配方预测模型打下基础。

3 配色算法构建及预测效果分析

3.1 Kubelka-Munk双常数理论配色算法

在实现Kubelka-Munk双常数理论的配色算法构建的过程中，是在已知各单色纤维的吸收系数K和散射系数S的前提下进行光谱反射率曲线的拟合以达到预测配方的目的，目标是为了实现在相同的波长下，预测样的K/S值与混色样的K/S值相同。即二者存在以下关系：

表4 相对值法拟合色差Tab.4 Color differences fitted by relative value method

(K/S)sλ=(K/S)mλ

(11)

式中：λ表示波长，nm；(K/S)sλ表示在波长为λ时预测样的K/S值；(K/S)mλ表示在波长为λ时，混色样的K/S值。

对于多组分混色预测样本，混色样K/S值与各组分单色纤维的K值和S值存在以下关系：

(12)

式中：C1+C2+…+Cn=1，各波长下每种组分单色纤维的吸收系数K和散射系数S是上文中通过相对值法计算得到的。

将上述公式展开移项得：

(13)

(14)

在各波长下，设

(15)

定义系数矩阵

因此线性方程转化为

Y=AC

(16)

由最小二乘法[8]求解可得各组分纤维

C=(AT×A)-1×A-1×Y

(17)

3.2 Kubelka-Munk双常数理论预测效果

为验证上述算法的准确性和可靠性，采用品红(M)、黄(Y)、青(C)3种单色纤维组合按照不同配比制备36种混色样作为目标样进行配方预测，样品制备方法、数量和测试方法与上文相同，在配方预测的基础上计算预测色差，以二者的准确性对预测模型进行评价。

在设定青色纤维各个波长下的散射系数均为1的基础上，计算出各色纤维各个波长下的K值和S值，在此基础上采用Kubelka-Munk双常数理论构建全色谱配色算法[9-10]对上述制备的36种混色样本进行配方预测和计算预测色差。部分样本的混合比例、CIELAB色度值和预测色度值、预测比例及即预测色差的结果如表5所示。

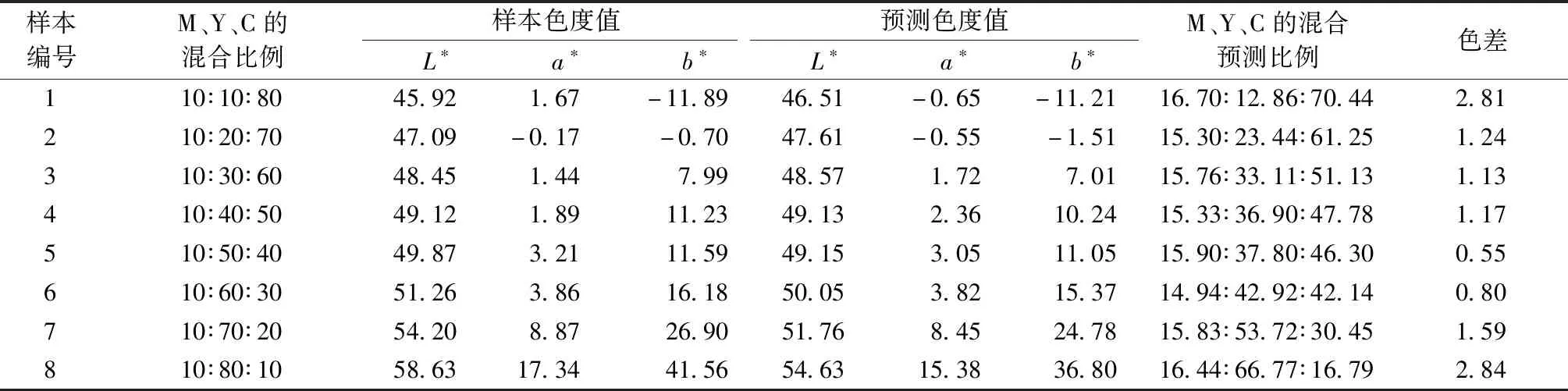
表5 Kubelka-Munk双常数理论预测结果Tab.5 Prediction results based on Kubelka-Munk double constant theory

注：M表示品红色纤维；Y表示黄色纤维；C表示青色纤维。

通过基于Kubelka-Munk双常数理论构建的全色谱配色算法对36种3次色混色样品进行了配方预测和预测色差，在此基础上，通过计算样本平均色差及各色差层级分布占比和预测样本的平均比例误差对预测的精度进行分析，其结果见表6，预测样本的平均比例误差如式(18)所示。

(18)

表6 Kubelka-Munk双常数理论测配色精度分析Tab.6 Kubelka-Munk double constant theory measurement color matching precision analysis

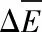
分析表6可发现，Kubelka-Munk双常数理论所预测的样本色差均值在可接受范围内，从色差分布来看，ΔE≤2的情况已经包含了绝大部分，且平均比例误差较小，色差预测效果优良，证明该模型适用于环锭数码纺混色纱的颜色预测。

4 结 论

本文以Kubelka-Munk双常数理论为基础对环锭数码纺混色纱测配色进行研究。采用相对值求解参数吸收系数和散射系数并进行模型构建；结合全色谱算法和最小二乘法进行配色算法的构建，从而实现对环锭数码纺混色纱的颜色预测与配方预测，在总体样本评价过程中，分别对预测样本色差均值、色差分布及预测样本的平均比例误差进行分析，证实了本理论模型的可行性。

环锭数码纺混色纱因富有立体感的纹理效果和独特的色彩呈现方式，符合现代消费者追求个性化、时尚化的服饰消费理念，有着广阔的发展前景。本文在环锭数码纺纱系统的基础上，对色纤维混色模型进行研究，并构建其测配色算法，对推进色纺纱智能化生产，提高色纺纱生产效率有重要意义。