从几何特性入手 圆锥曲线巧求解

甘肃省张掖市实验中学 宫 雪 734000

在高考中,圆锥曲线一般有两小一大三道题，一直是高考的重点、热点，也是难点；其中圆锥曲线客观题主要考查圆锥曲线定义、标准方程、几何性质（如渐近线、离心率等），渗透了数形结合、转化与化归、曲线与方程的数学思想方法，以发展学生的学科素养为导向，考查圆锥曲线的核心知识与本质特性，方法灵活多变，能力要求高，相当一部分学生对此无所适从,战战兢兢，下面以2019年高考数学全国Ⅰ卷理科第10题为例，进行知识与解法剖析，旨在拓宽读者思维视野，提高解题能力.

问题：（2019年全国Ⅰ卷理科第10题）已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点,若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为（ ）.

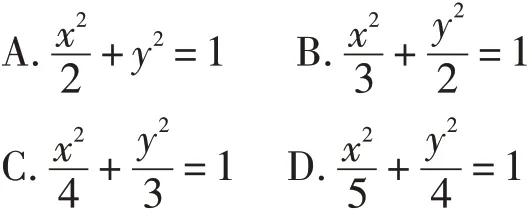
分析:本题表面看来朴素无华，内涵却很丰富，考查椭圆的定义、标准方程及余弦定理的应用，考查数形结合思想、转化与化归、方程的数学思想方法，很好的落实了直观想象、逻辑推理、数学运算等数学素养，具有很好的创新性；求解圆锥曲线试题,首先考虑画图,其次考虑定义与几何性质，充分挖掘图形几何量之间的等量或相互关系，凡涉及焦点三角形的问题,还应注意解三角形等知识的应用.

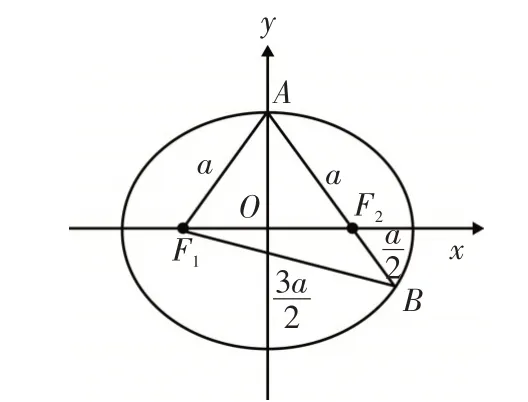
图1

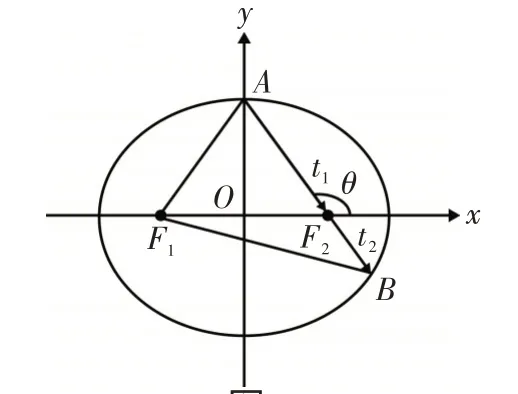
图2

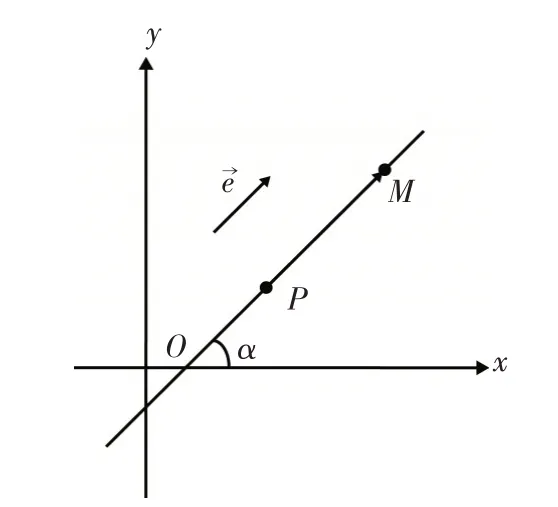
图3

若A,B为直线l上两点，其对应的参数分别为t1与t2，线段AB的中点为M，点M对应的参数为t0，则以下结论经常用到：①重在数形结合，理解记忆，切忌生搬硬套，牵强附会.

点评:灵活应用余弦定理是解题的关键,此方法也可换做在△F1F2B与△AF1B中求∠ABF1的余弦值.

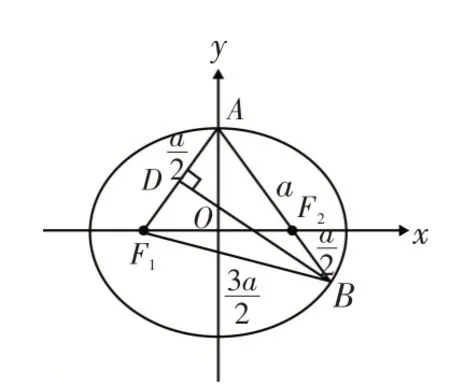
图4

图5

解法6：如图1所示，由已知可设|F2B|=t，则|AF2|=2t ,|BF1|=|AB|=3t，由椭圆的定义有2a=|BF1|+|BF2|=4t ,得又因为|AF1|+|AF2|=2a,所以|AF1|=a,所以点A应为椭圆C的上顶点（或下顶点）；如图5所示，过点B作BD垂直x轴于点D,则△AOF2∽△BDF2,相似比为2:1,得(a＞b＞0)上，所 以 满 足 其 方 程 得:b2=2,所求椭圆方程为，故选B．解法7：如图1所示，由已知可设|F2B|=t，则|AF2|=2t ,|BF1|=|AB|=3t，由椭圆的定义有2a=|BF1|+|BF2|=4t ,得又因为|AF1|+|AF2|=2a,所以|AF1|=a，所以点A应为椭圆C的上顶点（或下顶点）；如图6所示，由焦半径公式得，其中e为椭圆的离心率，p为焦点到准线的距离（简称：焦准距），右准线方程为:为直线AB的倾斜角；又因为得a2=3,又因为c=1,所以b2=2,所求椭圆方程为

图6

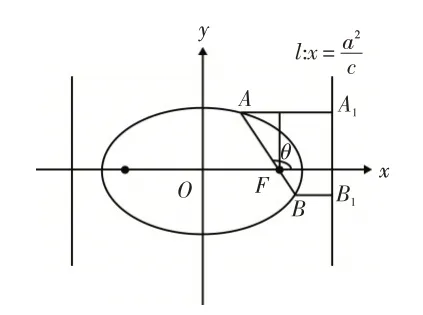
图7

点评：用焦半径公式几乎就是秒杀此类试题;焦半径公式的推导如下：椭圆的第二定义是平面上到定点F(c,0)（F不在l上）的距离与到定直线（椭圆的右准线）的距离之比为常数e（0＜e＜1）的点的轨迹为椭圆（注：人教A版选修2-1第50页）.如图7所示，AB是过椭圆的右焦点F(c,0)的一条弦，它的倾斜角为θ，p为焦点F(c,0)到准线的距离（简称：焦准距），过A做AA1⊥l于点A1，过B做BB1⊥l于点B1，则由第二定义得：|AF|=e|AA1|=e(p+|AF|⋅cosθ)，所以同理：

大部分学生对圆锥曲线试题有畏惧情绪,究其主要原因还是找不到解题的突破口或切入点,但从以上解析可以看出，抓住图形的某一几何特性，去转化、求解圆锥曲线试题，让学生在较短的时间内，突破思维障碍,快速准确地求解题目,事半功倍;另一方面,一题多解是提高解题能力的有效途径,它在呈现不同解法的同时,不但拓宽了学生思维的灵活性与深刻性,而且提高了学生解题的兴趣、品味、效率.