根在四棱柱，万变不离宗——谈数学建模素养的考查形式

云南省昆明高新区第三中学 唐明超 650106

广东省汕头市澄海华侨中学 潘敬贞 515800

1 借长方体模型考查基本量的计算

几何体基本量的计算仍然是考查的重点和问题解决的落脚点，体积与表面积的计算是考查的热点，如2019年全国Ⅰ卷理科12题考查三棱锥外接球的体积计算；2019年全国Ⅰ卷文科16题考查点到平面的距离计算等.用好长方体这个熟悉的载体，灵活地将多面体置于长方体中，将看似复杂的问题简单化，有效降低思维难度，甚至还可以基于空间直角坐标系用好坐标运算将定性的问题通过定量计算得以直观反映.

例1（2019年全国Ⅰ卷理科12题）已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为( ).

A.86π B.46π

C.26π D.6π

解析：如图1，假设PB⊥PA，PB⊥PC，PA⊥PC，易知该三棱锥是正方体的一部分，因为△ABC是边长为2的正三角形，所以PA=PB=PC=2，正方体外接球的半径为体对角线的一半，所以外接球的半径，经检验，假设满足条件∠CEF=90°，从而

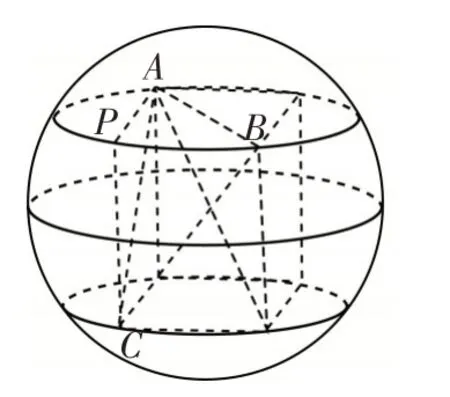
图1

例2 （2019年全国Ⅰ卷文科16题）已知∠ACB=90°，P为平面ABC外一点，PC=2，点P到∠ACB两边AC，BC的距离均为，那么P到平面ABC的距离为．

解法1：根据题目已知的几何关系可构建如图2所示的底面是边长为1，高为2的长方体，从而可直接得出P到平面ABC的距离为

解法2：借助如图3所示的长方体模型，设点P在平面ABC上的投影是点D，作PF⊥AC,PE⊥BC,所以AC⊥平面PED，所以AC⊥DF，同理BC⊥DE，所以四边形CEDF为矩形，又因为PE=PF,所以DE=DF，即四边形CEDF为正方形.所以CE2=PC2-PE2=1，在Rt△PDE中，PD2=PE2-ED2=2，所以P到平面ABC的距离为PD=

图2

图3

例3（2019年全国Ⅲ卷文理8题）如图4，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则( ).

A线.B BMM=，EENN是，且相直交D直线

B.BM≠EN，且直线BM，EN是相交直线

C.BM=EN，且直线BM，EN是异面直线

D.BM≠EN，且直线BM，EN是异面直线

图4

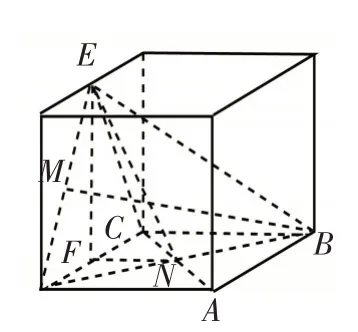
图5

解析：将题目已知的几何关系嫁接至如图5所示的长方体中，设正三角形△ECD的边长为2，则正方形ABCD的边长也是2；在Rt△EFN中，EN2=EF2+FN2=4，BC2=7，在△BDE中，BM与EN分别是DE与BD上的中线，一定相交，所以正确答案选择B.

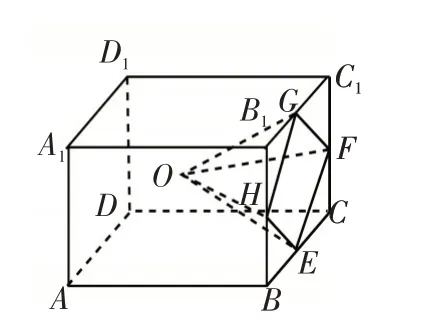
图6

例4（2019年全国Ⅲ卷文理16题）学生到工厂劳动实践，利用3D打印技术制作模型.如图6，该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H，分别为所在棱的中点，AB=BC=6cm,AA1=4cm,3D打印所用原料密度为0.9g/cm3，不考虑打印损耗，制作该模型所需原料的质量为

解析：该模型为长方体ABCD-A1B1C1D1,挖去四棱锥O-EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H，分别为所在棱的中点，AB=BC=6cm，AA1=4cm所以该模型体积为：VABCD-A1B1C1D1-VO-EFGH=132(cm3)，原料密度为0.9g/cm3，不考虑打印损耗，则所需原料的质量为132×0.9=118.8（g）．

题目背景为长方体，挖去一个四棱锥模型，虽然问题的呈现方式体现了与物理学科交叉，但是所考查的基础知识和基本思想体现了数学学科的思想性，充分体现了数学基础知识与基本思想方法的实际应用价值.

例5（2019年全国Ⅱ卷文理16题）中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美.图7右图是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有_____个面，其棱长为_______．

解析：该半正多面体共有8+8+8+2=26个面，截面可抽象为如图8所示的正方形内接正八边形，设其棱长为x，则解得.故答案为

图7 （左）

图7 （右）

图8

例6（2019年全国Ⅱ卷17题）如图9，长方体ABCD-A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，AB=3，求四棱锥E-BB1C1C的体积.

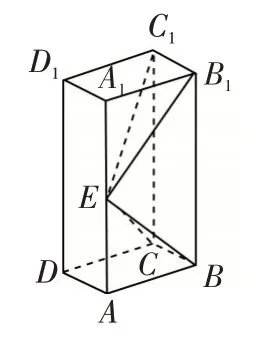
图9

解析：（1）略；（2）由（1）知∠BEB1=90°，由题设可知Rt△ABE≅Rt△A1B1E，所以∠AEB=∠A1EB1=45°，所以AE=AB=3，AA1=2AE=6，因为在长方体ABCD-A1B1C1D1中，AA1//平面BB1C1C，E∈AA1，AB⊥平面BB1C1C，所以E到平面BB1C1C的距离d=AB=3，所以四棱锥E-BB1C1C的体积

例7（2019年全国Ⅲ卷文理19题）图10（左）是由矩形ADEB、Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°．将其沿AB，BC折起使得BE与BF重合，连结DG，如图10（右）．（1）略；（2）（文）求图10（右）中的四边形ACGD的面积．

解析：（2）将折叠后的三棱柱放置于长方体的合适位置如图11所示，连接BG，AG，所以AG为长方体的体对角线，因为∠FBC=60°且AB=1，BE=BF=2，所以长方体长宽高分别为1，3，3，所以AG=13，在△ACG中，AC=5，CG=2，AG=13，可得，即有，所以平行四边形ACGD的面积为2

图10

图11

2 长方体模型中点线面位置关系的证明

例8（2019年全国Ⅱ卷7题）设α，β为两个平面，则α//β的充要条件是（ ）.

A.α内有无数条直线与β平行

B.α内有两条相交直线与β平行

C.α，β平行于同一条直线

D.α，β垂直于同一平面

解析：可借助长方体的边角关系并结合相关判定定理和性质定理容易得出正确答案B.

例9 同例6（2019年全国Ⅱ卷17题）（文理同题）（1）证明：BE⊥平面EB1C1；

证明：由长方体ABCD-A1B1C1D1可知，B1C1⊥平面ABB1A1，BE⊂平面ABB1A1，所以B1C1⊥BE，所以BE⊥EC1，B1C1⋂EC1=C1，所以BE⊥平面EB1C1；

例10同例7（2019年全国Ⅲ卷19题）（文理同题）（1）证明：图11中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；

解析：由已知得AD//BE，CG//BE，所以AD//CG，AD，CG确定一个平面，A，C，G，D四点共面，由已知得AB⊥BE，AB⊥BC，所以AB⊥面BCGE，因为AB⊂平面ABC，所以平面ABC⊥平面BCGE．

3 长方体模型中活用坐标系

例11同例6（2019年全国Ⅱ卷17题）理（2）若AE=A1E，求二面角B-EC-C1的正弦值．

解析：（2）以C为坐标原点，建立如图12所示的空间直角坐标系，设AE=A1E=1，因为BE⊥平面EB1C1，所以BE⊥EB1，所以AB=1，则E(1,1,1)，C A(11(0,1,0,0,2))，，CB(01(,00,,10,)2，)因，x为BC⊥EB1，所 以EB1⊥面EBC，故取平面EBC的法向量为，设平面ECC1的法向量0），所以面角B-EC-C1的正弦值为

图12

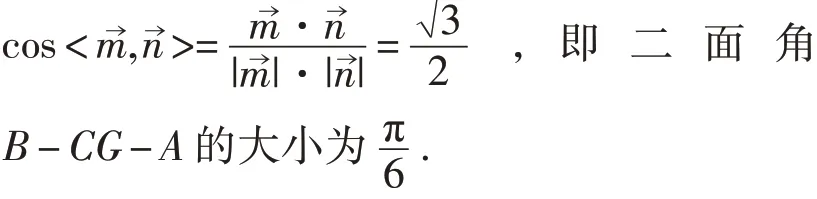
图13

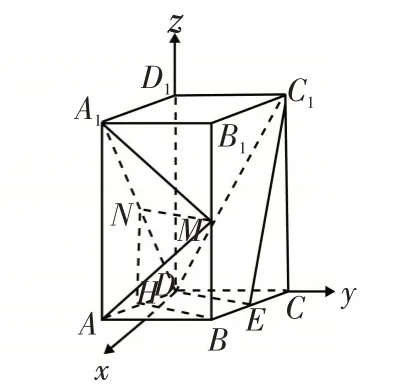
图14

4 一般四棱柱辅助解题

例13（2019年全国Ⅰ卷18题）如图14，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）（文理同题）证明：MN//平面C1DE；（2）（文）求点C到平面C1DE的距离；（理）求二面角A-MA1-N的正弦.

解 析：（1）证 明：如 图14，过N作NH⊥AD，则NH//AA1，且NH=AA1，又MB//AA1，MB=AA1，所以四边形NMBH为平行四边形，则NM//BH，由NH//AA1，N为A1D中点，得H为AD中点，而E为BC中点，所以BE//DH，BE=DH，则四边形BEDH为平行四边形，则BH//DE，所以NM//DE，因为NM⊄平面C1DE，DE⊂平面C1DE，所以MN//平面C1DE；

（2）过C作C1E的垂线，垂足为H.由已知可得DE⊥BC，DE⊥C1C，所以DE⊥平面C1CE，故DE⊥CH.从而CH⊥平面C1DE，故CH的长即为C到平面C1DE的距离，由已知可得CE=1，C1C=4，所以.从而点C到平面C1DE的距离为

该题背景不是长方体，也不具备借助长方体模型的条件，但是题目本身就是底面为菱形的直四棱柱，隐含着多组线线垂直关系，既可以考虑用几何分析法进行解答，也可以借助空间直角坐标系用坐标运算进行解答，入口宽、起点低、方法较多，如文科试题（2）题还可以考虑用等体积法求解点到平面的距离.

从以上分析可以看出，2019年高考立体几何试题的命制紧紧扣住《2017年版普通高中数学课程标准》相关要求，从客观题到主观题的问题设计都体现着以长方体为背景，考查点线面位置关系的证明，线面角、二面角、点到平面的距离计算；虽然2019年全国Ⅰ卷18题没有直接给出长方体，但背景是底面为菱形的直四棱柱，依然存在多组垂直关系，解题思想和方法基本一致.

万变不离其宗，四棱柱是常见几何体的母体，是立体几何试题命制的出发点，是数学建模核心素养考查的重要载体.空间观念的培养需要经历想图、作图、识图的基本过程，准确认识四棱柱的基本结构特征，准确理解四棱柱中点线面的位置关系，经历四棱柱的切割与还原过程体会常见空间几何体之间的逻辑联系，学会基于补体思想解决该类立体几何试题，化抽象为直观，降低思维难度，体会知识的发生与发展过程.