基于新型冠状病毒传播机理的交通出行易感度研究

张 毅，王雪成，毕清华

（交通运输部科学研究院，北京 100029）

0 引言

突如其来的新型冠状病毒肺炎疫情（Corona Virus Disease 2019,COVID-19）短时间内改变了绝大多数居民的生活方式，也改变了大众的交通行为。公共交通作为高密度的人员集散载体，为COVID-19等类病毒提供了潜在的传播扩散环境[1-4]，亟需在明确人群中病毒空气传播机理的基础上，研究乘坐交通载运工具的感染风险，为公共交通科学防疫、精准管控提供理论支撑。

1 病毒传播的基本理论及机理

1.1 病毒空气传播模型

根据病毒学相关理论，病毒传播系统包括潜在的传染源、传播途径和易感人群三个部分。呼吸飞沫核是空气传染疾病传播途径之一。病毒研究学者Wells在1955年提出了“quanta”概念[5-6]，其定义为使一个人达到致病量的最少病原体数目，基于此可确定空气传染病的感染概率。Wells指出，吸入一个quanta的人平均感染概率服从泊松分布，也就是有63.2%（即1-e-1）的概率会感染上空气传染病。Riley等根据古典的传染病感染概率预测方程，进一步发展了空气途径传染病感染概率方程。

Wells-Riley方程基于定量感染的概念，该方程表示为：

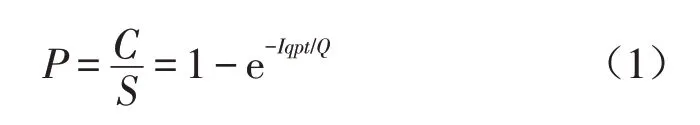
式（1）中：P为感染概率；C为感染人数；S为易感人数；I为感染者，q为一个感染者的quanta产生率；p为呼吸通风量（m3/h）；Q为空间通风量（m3/h）；t为暴露时间（h）。

Seppanen等考虑了空气过滤器和颗粒沉降效果，发展了Wells-Riley方程，得出如下方程：

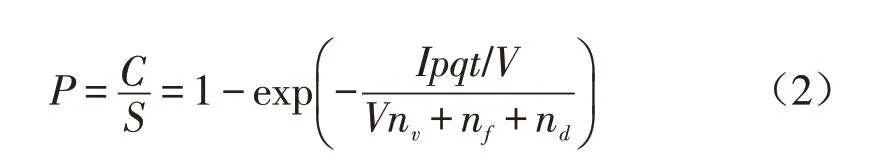
式（2）中：V为体积（m3）；nv为换气次数，nv=Q/V（次/h）；nf为回风量与过滤器过滤效率的乘积；nd为飞沫核沉降在室内表面上的数量。

Fennelly等在考虑了口罩和空间消毒等的作用后，将Wells-Riley模型发展为：

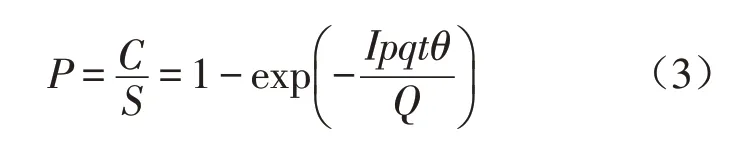
式（3）中：θ为口罩的渗透系数，取值范围为0～1,θ=1时，表示飞沫核能够完全渗透到人的呼吸区，属未戴口罩或者口罩完全不起作用的情况。

1.2 COVID-19的传播病理参数

依据相关研究和已发布的防护指南等[7-9]，COVID-19符合空气传染病的基本传播机理，主要依靠接触和飞沫传播。关于COVID-19的传染强度，引入基本再生数（Basic Reproduction Number）概念R0。R0是指没有干预的情况下，在一个全部是易感人群的环境中，平均一个患者可以传染的人数，即自由传播情况下一个病人平均能感染多少人。该指标是广义层面描述病毒传染强度的数值，只要基本再生数大于1，病毒则会广泛传播；小于1，病毒就不能广泛传播。关于COVID-19的基本再生数的研究已有相关的文献，本文根据《人民日报》（和丁香园一起发布）疫情实时动态数据，通过建模评估得COVID-19的R0在3.2～3.9之间，该值是目前研究的高位值。

不同的疾病和不同的感染者个体所产生的quanta值不同，当感染者所呼出的病原体特别多，quanta值特别大时，感染者容易感染他人，从而导致疾病暴发。表1展示了有明确研究分析记录[7,10]的肺结核、麻疹、甲型H1N1流感及SARS的quanta产生率。

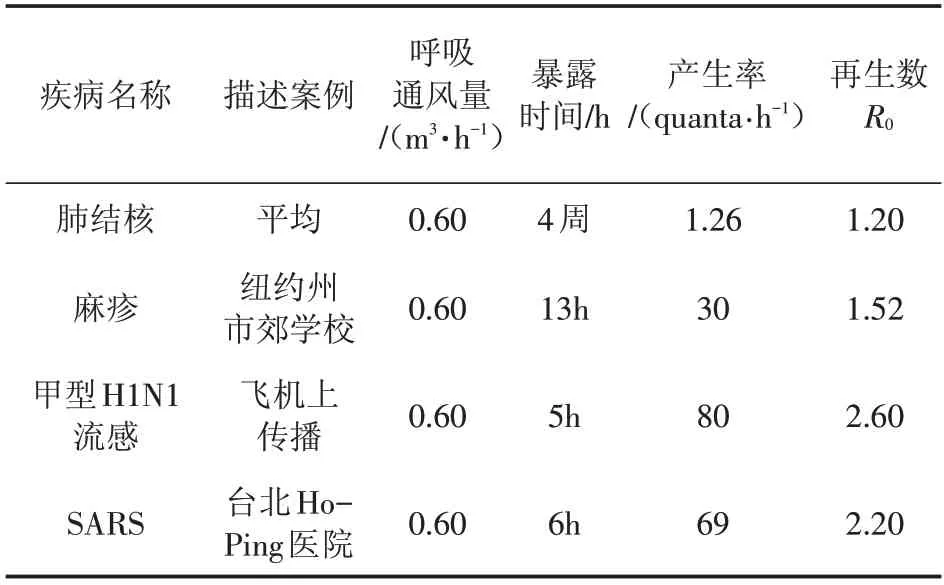
表1 肺结核、麻疹、甲型H1N1流感及SARS的quanta产生率

现阶段对COVID-19的quanta值还未见确切的病理案例，本文综合肺结核、麻疹、甲型H1N1流感及SARS的再生数与已知的quanta产生率间的关系，估算COVID-19的quanta值在100～122之间。考虑到长途城际出行时，乘客静坐时间较长，呼吸较为稳定，因此quanta取值100；而城市内出行时，乘客站立概率较大，quanta取值122。

2 交通出行易感度模型的建立

2.1 交通出行易感度计算模型

疾病传播具有相当的复杂性，依据传染病的传播理论，可以将交通出行环境和参与者作为一个系统研究，即一次公共交通出行的环境及其参与者共同构成一个复杂系统。该系统满足传染病传播的三个基本条件：潜在的传染源、传播途径和易感人群。

借用传染病学中易感染者的感染概率定义，本文提出交通出行易感度概念，指乘客通过乘坐交通载运工具接触到陌生个体中的感染者且被传染的概率。决定该风险程度的因素较多，本文对其参数化，建立交通出行易感度计算模型，即计算在交通工具内健康者被感染的概率Pi，计算公式如下：

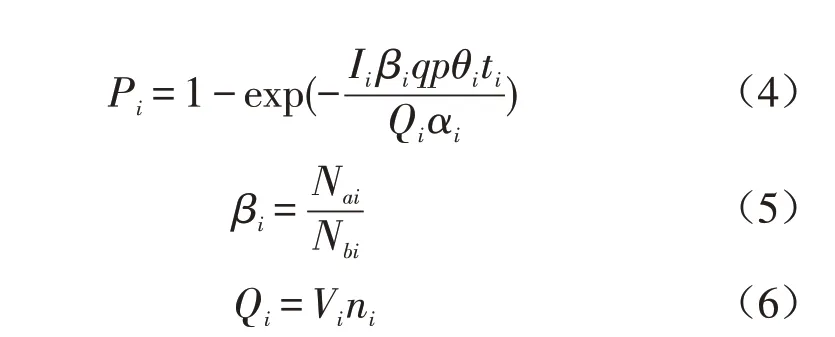
式（4）～式（6）中：βι为第i种交通运输工具的实际载荷率；Nai为第i种交通运输工具的实际载客人数；Nbi为第i种交通运输工具的标准额定载客人数；p为乘客呼吸量（m3/h）；q为一个感染者的quanta产生率;Qi为第i种交通运输工具通风量（m3/h）；Vi为第i种交通运输工具的体积（m3）；ni为第i种交通运输工具每小时通风次数（次/h）；ti为乘坐第i种交通运输工具暴露接触时间；αi为第i种交通运输工具消毒措施带来的保护系数（取值范围为0～1）；θi为乘坐第i种交通运输工具乘客佩戴口罩的渗透系数（取值范围为0～1）。

将式（5）和式（6）代入式（4），可得式（7）：

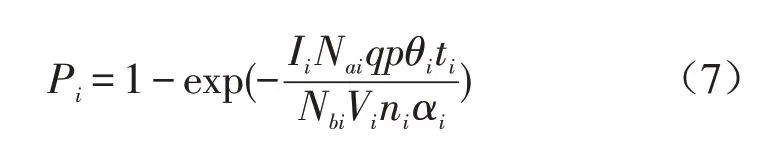
由式（7）可看出，Pi与交通运输工具的载客密度、乘坐时间、感染人数成正向关系，人员密度越小、通风量越大、防护系数越高则易感度越低。将病毒空气传播模型应用于交通运输系统的实践中，构建交通出行易感度模型，其中每个参数都对感染的概率有很大影响。系数I在交通系统中即乘车的感染者数量。如果能确保参与到交通系统的感染者数量为0，则在交通出行中被传染概率自然为0。如同行乘车人员固定且人员健康状况和接触数据清晰，比如在直达班车等情况下人员随机程度降低，则系数I可控。在疫情暴发期，各运输企业普遍采用对乘客进行体温检测的措施，设置临时检疫站筛查感染人群，相当于发现并隔离传染源。但根据《新型冠状病毒感染的肺炎诊疗方案（试行第五版）》，无症状感染者也可能成为传染源，因此可能会出现没有症状的感染者通过体温检测后乘坐了交通运输运载工具的情况。鉴于此，交通筛查率和交通有效筛查率可通过式（8）、式（9）表述：

源感染者的quanta产生率或源强度通常恒定。在公共交通出行中，S为易感人数，视为乘坐运载工具（小汽车、公交、飞机、地铁车厢等）的总人数。运载工具的空间恒定，因此实际载荷率越低则S值越小，乘客自然分布在车厢内，人均距离越大即空间越大，人员密度越低，接触到源感染者产生的quanta越少。

2.2 核心参数设定

此模型中的参数可分为三类：（1）交通工具参数：交通工具的体积V、最大载员N、乘客出行时间t等，均可根据实际情况获得（见表2）；（2）病理参数：感染者的病毒quanta产生率q，乘客呼吸通风量p；（3）人为控制措施的定量化参数：携带病毒人数I、交通工具通风量Q、口罩渗透系数θ、消毒防护指标α，均为实际防治措施的定量化评估指标。

2.2.1 交通工具参数

我国交通工具种类繁多，为简化研究样本，本文选取典型的交通工具对其参数进行量化。城市交通的出行方式包括步行、自行车、私家车（分轿车和SUV）、出租车、公交车（分超大型、中型、小型）、班车、地铁（分A、B类车型）。城际交通的出行方式包括民航（以波音737、空客A320为例）、高铁（以和谐号CRH5、复兴号CR400二等座车厢为例）、普通铁路（以硬座和硬卧车厢为例）、城际客运大巴，这些交通方式的具体参数如表2所示。

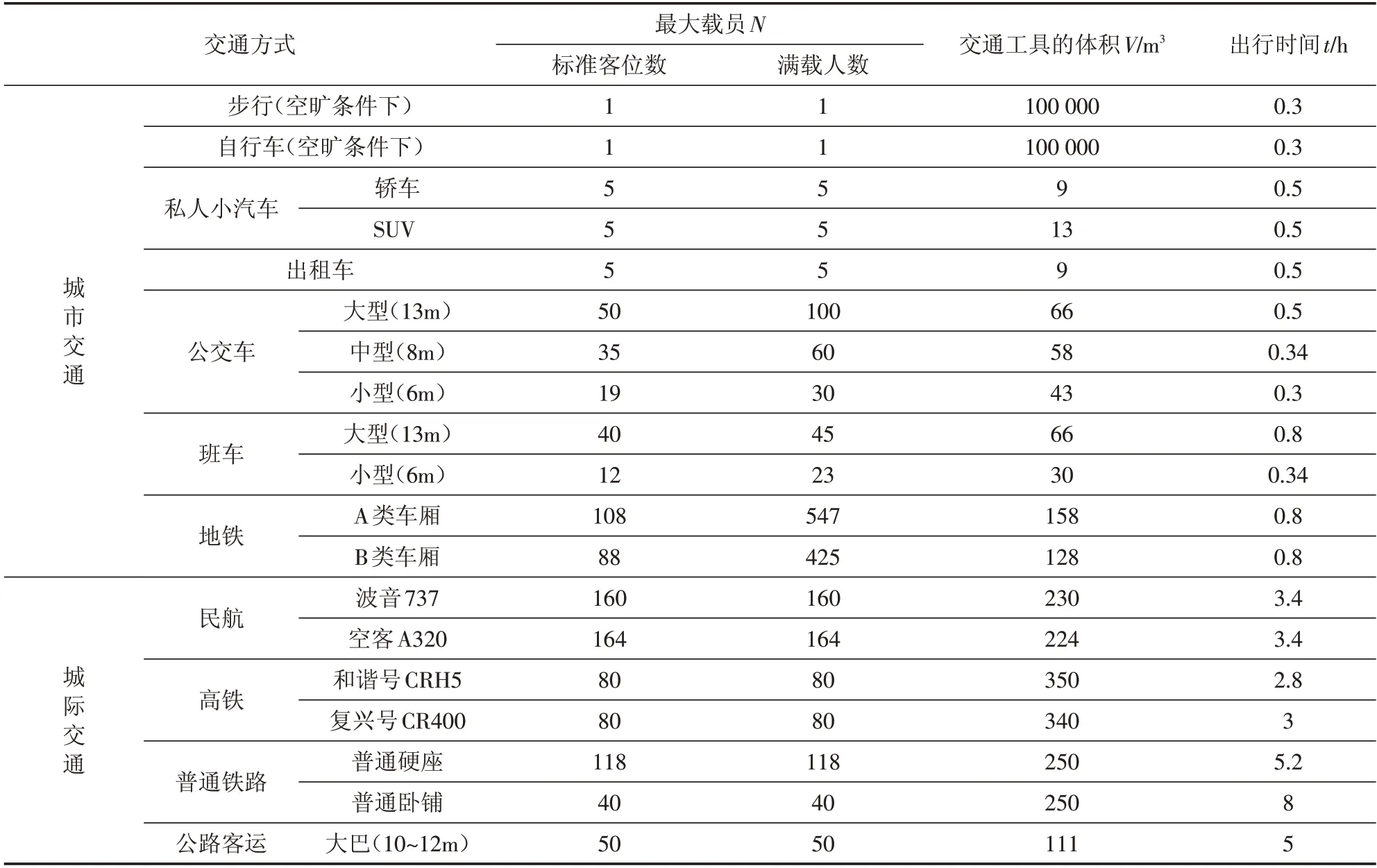
表2 不同交通出行方式参数

2.2.2 人为控制措施的量化参数

（1）携带病毒人数I

系数I在交通系统中即乘车的感染者人数。由于在疫情暴发期，各运输企业普遍采用对乘客检测体温等措施，设置临时检疫站筛查感染人群，相当于发现并隔离传染源，但有尚在发病潜伏期却具备传染性的人员参与交通活动的可能性。根据目前数据，携带病毒者乘坐交通工具为极小概率事件，如根据2020年2月16日统计的全国已确诊COVID-19病例数和当日总出行量计算，I值小于0.0001，接近于0。但本文的侧重点为分析不同交通出行方式的传染概率，故在计算中I值取为1，即假设在一次乘坐交通工具出行中有1名同行乘客为感染者。

（2）交通工具通风量Q

不同交通工具有相应的空调设计标准，标准中重点对空调冷、热负荷系数及功率进行了规定，可据此计算得出通风量。本文选择各种运输方式的典型型号，收集各交通工具的通风量[10-13]，并根据各种交通工具的核定客位计算人均通风量。

不同交通运输工具通风量具体数据见表3。

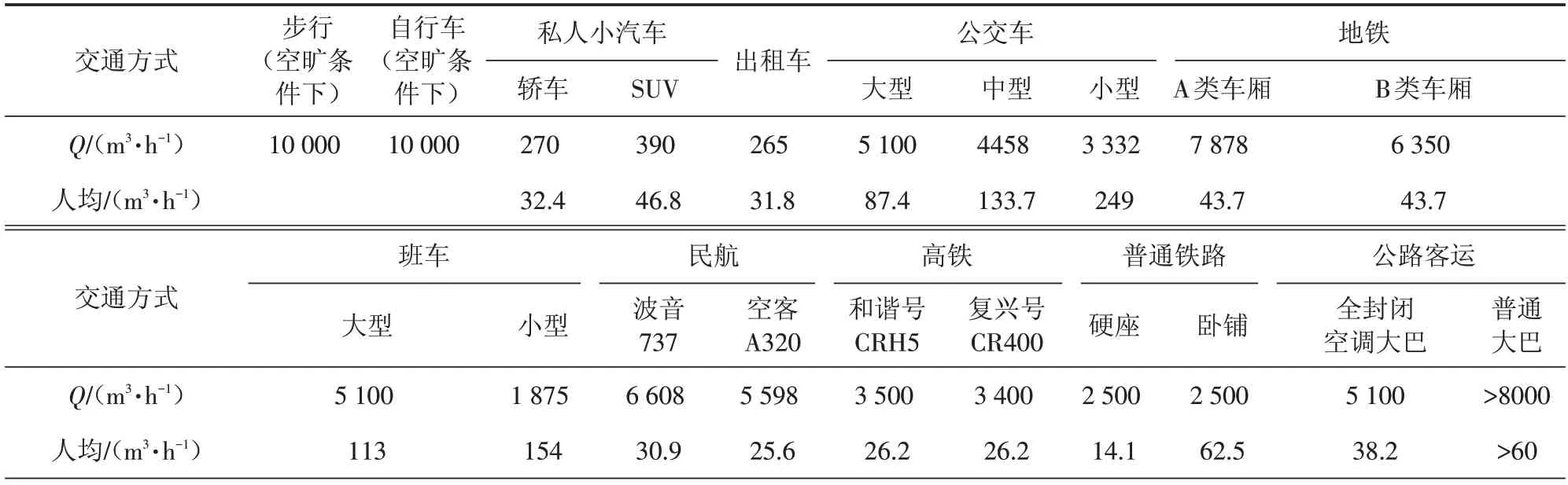
表3 不同交通运输工具的通风量Q

（3）防护参数θ和α

防护参数主要体现要求乘客佩戴口罩、对交通工具进行消毒等防疫措施。在参数设定时，口罩保护系数θ取统计的数值0.2%；对于消毒指标α，不同交通工具取值不同。

3 情景分析与评估

3.1 基本假设和情景描述

如前所述，假设不同交通工具中有1名乘客为COVID-19感染者，该感染者的quanta量为100～122。本文视同一运载工具为一整体，暂不考虑载运工具内感染者的位置和其他乘客与该感染者的距离。

根据前文参数，分别计算不同交通出行方式的感染概率，每种交通方式有三种情景，即基准情景、高危（最坏）情景、采取防控措施情景。

基准情景：运载工具载客量为核定载客量，取常规的空调系数（最大负荷0.6），有基本的消毒措施，但司乘人员均未佩戴口罩。

高危（最坏）情景：运载工具全封闭，未开车窗，也未开空调外循环或新风系统（通风系数为载运工具密闭条件自然透气的系数，一般为空间风量的0.2左右），满载，没有基本的消毒措施，司乘人员均未佩戴口罩。

采取防控措施情景：运载工具载客量为核定载客数量的1/2，即实载率取50%；所有运载工具取最大的通风系数或可开窗的均开窗通风；采用消毒措施；司乘人员均佩戴口罩。

3.2 各类交通工具出行易感度计算

根据前文的假设情景，将相应的参数代入交通出行易感度计算模型，得出不同交通出行方式的易感度（见表4）。从表4中可看出，各种交通出行方式的易感度有一定的差异，步行、自行车方式（均为空旷条件下）下，人员间隔随机可控，易感度基本为零。在同行乘客有1人为COVID-19感染者的假设前提下，在高危情景中，私人小汽车、出租车、普通硬座、全封闭空调大巴几种交通方式的易感度概率均在10%以上。而在采取防控措施情景中（口罩、消毒、防护、降低人员密度），所有的交通出行方式易感度概率均在1%以下。

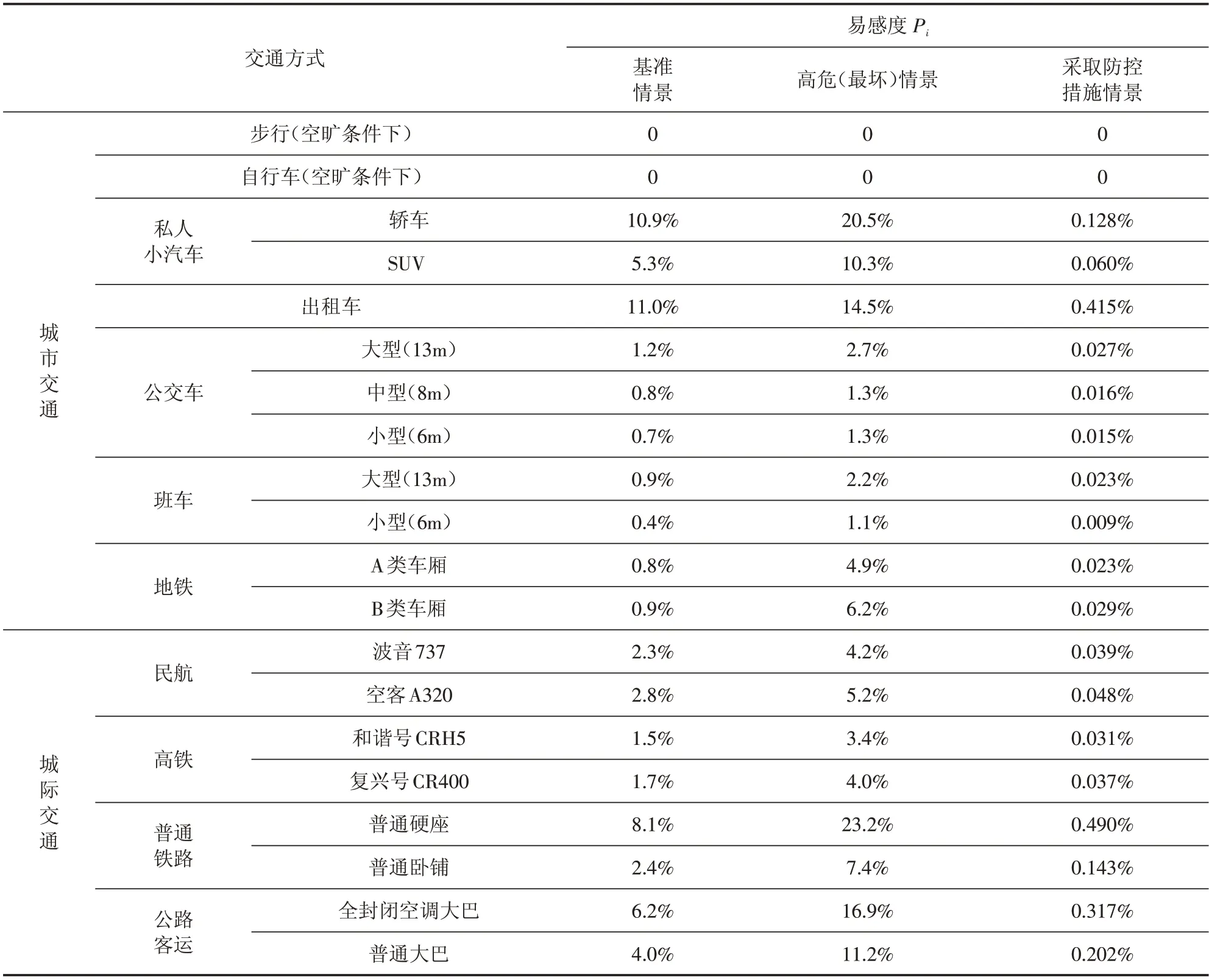
表4 不同情景下各类交通出行易感度

3.3 疫情防护措施的实施效果

根据COVID-19的传播特点，通过情景设置，可得到不同交通工具采取正确的疫情防控措施后的易感度，如图1所示。

由图1可以看出，通过采取正确的防护措施可大幅降低各种交通方式的易感度，对于公共交通工具，通过提高通风量、提升消毒效果、降低乘客密度及要求乘客佩戴口罩等措施能有效降低病毒的传播概率，在各种防控措施均被采用的情景下，乘坐交通工具的易感度相比高危情景降低97%以上，相比基准情景降低93%以上。

城市交通中，步行和自行车出行一直处于自由通风的环境中，而且人员间距能自动控制，因此与病毒接触的概率几乎为零，但保险起见同样需做好佩戴口罩等防护措施。

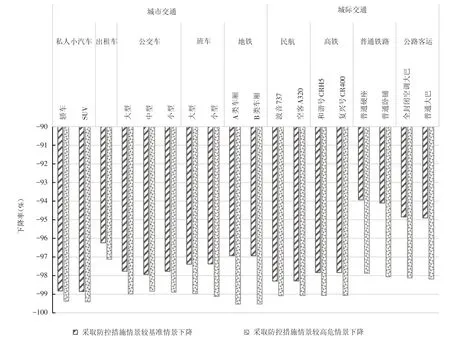
图1 采取防控措施情景下感染概率下降率

4 结论

依据传染性疾病的传染特征基础模型，在已知的COVID-19传染特征基础上，建立交通出行易感度模型，通过该模型可进行各种运输方式的感染风险概率量化和安全评估。

考虑到COVID-19潜伏期无症状的特征，在假定同行乘客中有1名为COVID-19感染者的极小概率前提下，进行了基准、高危、采取防疫措施三种情景的风险比对，得出以下结论。

（1）各种交通出行方式的易感度有一定差异。在高危情景下，普通硬座火车易感度为23.2%，公路客运全封闭空调大巴、私人小汽车等交通方式的易感度风险均在10%以上，相对较高。而运输工具中的通风系数与人员间隔是除口罩外的降低感染风险的重要参数，为此传统超高人员密度的地铁、公交等交通工具在疫情暴发期必须控制实载率。

（2）步行、自行车在空旷条件人员间距随机可控的前提下，易感度基本为零。

（3）通过所有人员戴口罩、运载工具消毒、降低运载工具内人员密度等措施，在采取疫情防控措施假设情景中，所有的交通出行方式易感度均可下降到1%以下。

（4）飞机、高铁、大巴等载运工具的典型型号，在空调最大换风系数下人均通风量可达到30m3/h左右，与室内通风标准的基本要求相当，因此这些运输工具配合适当的防控措施，不足以造成病毒大面积传播。但普通铁路硬座列车相对人均换风系数较小，有待进一步研究提高通风能力。

（5）暴露时间同样是影响感染概率的核心参数，应当加强长距离运输工具如全封闭的公路客运大巴的防护等级。

（6）本文是在已知的COVID-19感染特征和quanta产生率高位值等前提下，将运输工具和其中乘客作为整体进行分析，未考虑交通工具内个体与感染者距离等因素，随着COVID-19病理逐步明确，研究可进一步深化。