教学质量评价的模型设计
2020-03-04张学燚温永仙
张学燚 温永仙

摘 要:文章研究了高校教学质量评价的问题,以某高校数学专业为例,利用学生的成绩,构建出包含平行班级模块、平行年份模块、课程群模块的数学模型,用模块得分评价数学专业不同班级、不同学年、不同课程群之间的教学质量,用模型得分评价数学专业整体的教学质量;从模型实证的结果可以看出,文章构建的数学模型能较好地体现出一个专业在不同班级、不同学年、不同课程群这三个维度上的差异,能对专业的教学做出合理的评价。
关键词:教学质量评价;专业;模块化;集群化
中图分类号:G642 文献标志码:A 文章编号:2096-000X(2020)07-0006-05
Abstract: This article studies the problem of evaluating the teaching quality of colleges and universities. Taking a college mathematics major as an example, using the students' achievements, a mathematical model including parallel class modules, parallel year modules, and course group modules is constructed.The module scores are used to evaluate teaching quality about among different classes, different year and different courses major in mathematics. The model score is used to evaluate teaching quality for the whole major in mathematics. The empirical results of model can be seen that the constructed mathematical model in this paper can better reflect the differences of a major from three dimensions, namely different classes, different academic years and different course groups. It can made reasonable evaluation of professional teaching.
Keywords: teaching quality evaluation; professional; modular; clustering
一、概述
21世纪,最抢手的资源是人才,人才的产生离不开学校的教育,而教学评价是高校教育的重要环节,从这个意义上讲,建立一个有效的教学评价体系,对学校的教学至关重要。教学质量评价体系的建立,一方面能够让教师在日常的教学工作中发现自己的优势和不足,发挥一定的价值导向功能,另一方面,也能够使学生更清楚的了解自身的学习情况,做出针对性的学习计划。
早在19世纪初的英国就开展教育评估,经过几十年的发展,后来在Horance Mann等人的推动下,美国开始用学生的成绩进行教育评估。此后,随着多种标准化的测验表被编制出来,西方国家的教育评估得到了很好的发展。近年来,西方学者又作了很多有关教学评价的实践研究,比如, Anne Watson等人[1]研究了教师在课堂中的举例对教学质量的影响,他们从数学教学中出现的实例与对应数学对象的类别之间的关系入手,探讨了实例与数学对象类别之间的关系,并进一步论证了例子和例子之间的关系依赖于人类的能动性;Kejun Sun[2]运用模糊综合评价(PCE)的方法研究了大学生公共体育课程的教学评价问题;Shaun Michael Burns等人[3]研究了学生的出勤率对教学质量的影响,他们在控制班级规模、教师可用性和小组互动的基础上,探究学生上课需求评分,扩展了教学质量评估的研究。
我国教育评估的历史源远流长,有学者[4]指出早在西周时期,就已经建立管理与考核学生成绩的制度。进入21世纪,随着中国经济的快速发展,人民生活水平的显著提高,越来越多的人关注教育,研究过教学质量的评价问题。王彦雨[5]研究了高校教学质量的监控体系,他认为在教育发展的新形势下,要保证高校教学质量稳步提高,实现办学规模与办学质量、办学效益的均衡协调发展,就必须构建科学系统有效的教学质量监控体系;付惠[6]研究了改革开放以来中国高校教师教学评价方法的演化进程,她从教育史的角度出发,对我国高校教师教学质量评价的发展过程进行梳理;韦丽娃、丛彬龙等人[7]研究了基于学生表现的教学评价,他们运用层次分析模型对高校教学质量进行评价。
目前较为流行的CIPP课程评价模式由美国著名教育评价专家斯塔弗尔比姆于20世纪六七十年代提出,CIPP课程评价模式亦称决策导向或改良导向评价模式,它认为评价就是为管理者做决策提供信息服务的过程;中国学者袁琴[8]以商业摄影课程评价为例,全面介绍了CIPP评价模型在教学评价中的应用——即按照CIPP模型的思想,首先确定商业摄影课程评价由背景评价、输入评价、过程评价、结果评价等四个环节构成,然后确定各个环节的评价内容和评价标准,进一步确定评价等级,最后作出最终评价;CIPP评价是一种有效的课程评价方法,但是在评价过程中更多专注于描述性信息,很少有人从设计数学模型的角度进行量化分析,本研究是在改进传统CIPP评价模型的基础上,利用高校某专业学生的成绩构建一个基于学业成绩、可以量化的教学质量评价模型,依据模型得分来判断该专业的教学质量情况,并以此给出教学建议,改变当前教学评价在评價方法上单一的现状。
二、教学质量评价模型
为了能较好的评价专业的教学质量,本文分别从平行班级模块、平行年份模块、课程群模块这三个维度对高校某专业的教学质量进行评价,其中,平行班级模块能有效反应出专业各班级间学生成绩的截面差异,平行年份模块能有效反应出专业各学年间学生成绩的时间序列差异,课程群模块,能有效反应出课程群之间的差异,通过这三个维度的评价,进而对专业的教学质量做出综合性的评价。
(一)专业平行班级模块比较
我们用箱形图[9]来反映各班成绩数据的分布特征,数据集的箱形图由箱子和直线组成,有六个数字特征,分别是下截断点Min、第一四分位数Q1、均值、中位数M、第三四分位数Q3、上截断点Max,如图1所示。
若有L个平行班级,各班之间任课老师相同时,可以通过比较Q1,i(第i个班的第一个四分位数,i=1,2,…,l)、i、Mi、Q3,i(第i个班的第三个四分位数,i=1,2,…,l)来评价每个班级的成绩状况。若i、Mi接近(相对差异不超过5%),说明各平行班级之间总体成绩没有显著差异;若Mi差距较大(相对差异超过5%),则说明各班学生的基础、学风等差异较大;若Ri较大,则说明班级内成绩两极分化显著,其计算公式为:
Ri=Maxi-Mini (1)
各班之间任课老师不同时,若各班之间i、Mi差异较大,则M较大的班级整体水平较高,可以采用三阶均值Ai(i=1,2)来衡量班级之间的整体水平,计算公式为:
Ai=Q1,i+Mi+Q3,i (2)
(二)专业平行年份模块比较
用经济学中弹性的概念来刻画不同年份间学生成绩的变化情况,弹性的一般化定义可表述为一个变量(Y)的变化率(?驻Y/Y)与另一个变量(X)的变化率(?驻X/X)的百分比,数学表达式为:
根据刘芳[8]将学生的成绩划分为N等级,并赋予不同的权重Wj,计算公式为:
Wj=(N+1)-j (4)
用 表示第i个班级期初成绩属于第j等级的人数,用bi,j(i=1,2,…,l;j=1,2,…,n)表示第i班的期末成绩属于第j等级的人数;第i班学生总数为Pi,计算公式为:
(5)
则各班期初、期末成绩为Di、Ei,计算公式为:
用弹性来反应各班期初、期末成绩的相对变化程度[10],计算公式为:
(三)专业课程集群模块比较
集群化处理,能较好的反应出群体间的差异,是评价群体特征常用的方法,将具有某些共同特征的课程组成一个课程集群,这样就可以在群体间进行比较,如图2所示。
图2 专业课程群划分示意图
设i班的人数Pi与课程S的成绩满足一一对应的映射关系,根据课程难易程度、专业相关性等将专业所开设的课程划分为K个课程群,每个课程群包含i1(i1?叟2)门课程,求出课程群K.的一类测度值为L(课程群的加权算术平均),课程S.的一类测度值为H(课程的加权算术平均),在不同课程群K.之间进行多重比较,用V的三均值作为评价指标,计算公式为:
需要注意,上述方法的实现基于课程S.满足内部一致性检验,若S.差异显著(P?燮0.05),可把最大的V所对应的S.视为无效课程,将其从K.中剔除,重复此过程,直到S.通过内部一致性检验。
(四)教学质量评价总模型
基于前文的分析,可得到专业的教学质量评价模型(Teaching Quality Assessment Model,记为TQA模型),模型可表述为:
其中,
TQA模型由平行班级评价模块、平行年份评价模块、课程集群评价模块构成,其中,Y表示模型得分,评价专业的教学质量时可以以Y的大小作为评价依据;Ai表示平行班级模块得分,评价专业各班级间的教学质量时可以以Ai的大小作为评价依据;?着i表示平行年份模块得分,评价专业各年份间的教学质量时可以以?着i的大小作为评价依据;?撰表示课程群模块得分,评价专业课程群间的教学质量时可以以?撰作为评价依据,模块系数依次为?琢,?茁,?酌,满足?琢+?茁+?酌=1,其中?琢,?茁,?酌的值可由学校退休教师组成的学术委员会给出[11]。
三、TQA模型的应用
为了说明TQA模型,下文以某高校数学专业为例,数学专业《数学分析》通常分为《数学分析》I、《数学分析》II和《数学分析》III,平行班级之间的教学评价,我们以数学专业1班、数学专业2班的《数学分析》I的成绩为例;平行年份之间的教学评价,以《数学分析》I和《数学分析》III的成绩分别作为期初、期末成绩;课程群设定时,将数学专业的全部课程分为三个课程群。
(一)数学专业平行班级的成绩评价
选取数学专业1班、数学专业2班《数学分析》I的成绩,绘制出图3、图4;需要注意,当学生有补考或者重修时,用算术平均值作为最终成绩;绘图时,若发现奇异点,要回到数据中查找原因,在能确定奇异点对教学评价无显著影响时,可将其从样本中剔除。
由图3、图4知,Min1=47,Q1,1=61,1=66.173,M1=65,Q3,1=78,Max1=89,Min2=35,Q1,2=60,2=64.887,M2=63,Q3,2=76.7,Max2=95,進一步可知,
整理得到表1。
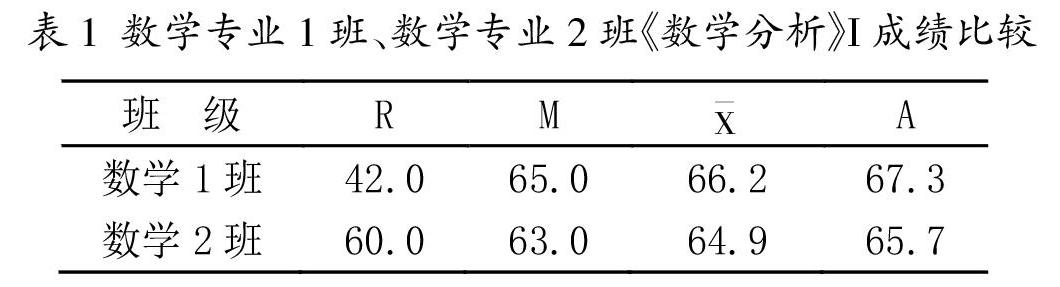
表1 数学专业1班、数学专业2班《数学分析》I成绩比较
从表1可以看出,两个班的中位数、均值非常接近,中位数偏出不超过3.2%,均值的偏差不超过2.1%,说明两个班级间《数学分析》I成绩没有显著差异,均值和三均值通过一致性检验(P=0.43>0.05),数学1班整体水平优于数学2班。同时也注意到,数学2班的极差较大,说明数学2班有两极分化的趋势,而数学1班该特征不显著。
(二)数学专业平行年份的成绩评价
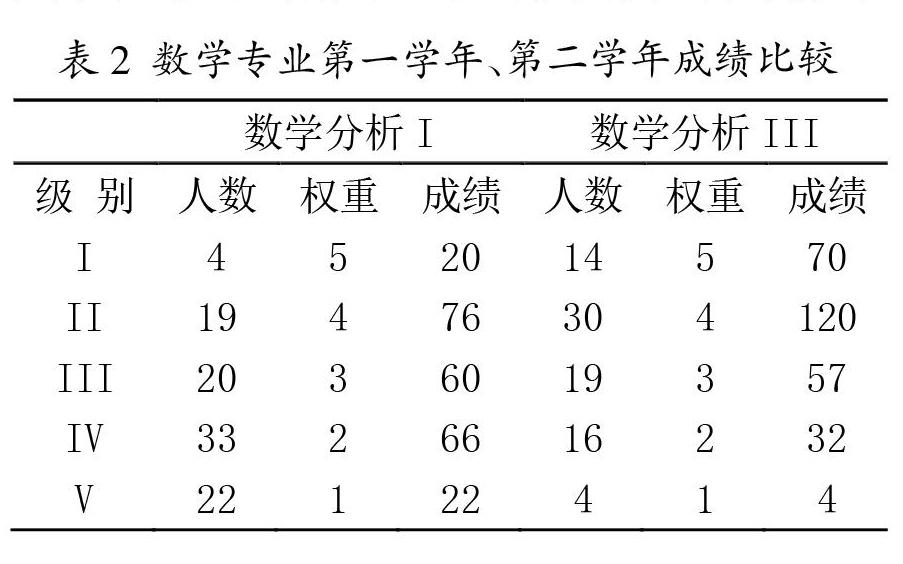
选取《数学分析》I和《数学分析》III的成绩作为期初、期末年份的成绩,并将成绩划分为五个等级(N=5),分别是优(I)、良(II)、中(III)、及格(IV)、不及格(V),并赋予权重Wj,j=1,2,3,4,5;计算出数学专业的Di、Ei、?着,得到表2。
由表2可计算出,
可以看出,相比于期初年份,期末年份数学分析的成绩有进步,进步率为36.9%,進步非常显著(P=0.00798<0.01)。
(三)数学专业课程群的成绩评价
将数学专业开设的全部课程分为三个课程群(K=3),分别是公共课课程群、科内基础课课程群、专业核心课课程群;计算课程群的一类测度值L,计算结果如(17)、(18)、(19)所示,课程S的一类测度值H.如表3所示。
H.进行一致性检验,K1,2、K1,3、K2,3的P值依次为
0.0918、0.1444、0.5668,均大于0.05,说明K.内S.差异不显著,课程群内部一致性检验通过,画出K.中H.的箱形图,找出各个课程群的、Q、M、Q,得到表4。
表4 公共课、科内基础课、专业核心课比较
根据表4,可计算出用V的三阶均值,计算结果如(20)、(21)、(22)所示:
三个课程群中专业核心课的测度值最大,科内基础课的测度值最小,二者相对差异为0.076758(>0.05),差异不显著,说明数学专业学生的成绩整体稳定,课程群划分合理。
(四)数学专业教学质量最终评价
基于上述分析,选择三组常见的模块比例系数[12],计算TQA模型得分,如表5所示。
表5 不同模块系数下TQA模型的得分表
假定课程群三阶均值的算术平均值为课程群模块的得分,平行班级三阶均值的算术平均值为平行班级模块的得分,以第3组系数为例,?琢:?茁:?酌=1:2:1,则数学专业1班、数学专业2班的TQA模型得分为Y1、Y2,数学专业(包含数学专业1班、数学专业2班)的TQA模型得分为Y,计算结果如下:
依据模型,算出数学专业得分为53.82;表明数学1班整体上优于数学2班,这与平行班级模块的结论一致,说明模块系数设定合理。若想进一步比较专业间教学质量的差异,还需要知道一个评价的参照,可用同样的方法计算另一个专业的模块、模型得分,依据分数作进一步的比较,也可由专家给出评价标准,依据分数所对应的等级对各专业的教学质量打分。
四、结论
TQA模型能有效反应出高校某专业的教学质量。从评价方法上看,TQA模型体现了模块化、集群化的思想,由学生课程成绩划分模块,由模块构成模型,层层递进,逐层打分,综合评价;从评价结果上看,TQA模型中,平行班级模块能有效反应出某专业各班级间学生成绩的截面差异,平行年份模块能有效反应出专业各学年间学生成绩的时间序列差异,课程群模块能有效反应出课程群之间的差异;从评价方法的对比上看,TQA模型克服了传统的CIPP评价模型只关注描述性信息的局限,TQA模型通过构建数学模型的方式对教学质量作量化分析,在实际的教学评价中更加客观公正。同时,TQA模型也有一些缺陷,比如,模块的评价指标过于单一、模块系数的确定不够客观等,这些方面的研究有待继续深入。
参考文献:
[1]Anne Watson,Helen Chick. Qualities of Examples in Learning and Teaching[J]. ZDM Mathematics Education, 2011, 43: 283-294.
[2]Kejun Sun. Physical Education Quality Evaluation Method Based on FCE [J].International Conference on Smart Grid and Electrical Automation, 2017: 518-521.
[3]Shaun Michael Burns, Larry H.Ludlow. Understanding Student Evaluations of Teaching Quality: The Contributions of Class Attendance[J]. J Pers Eval Educ, 2005, 18: 127-138.
[4]赵子江.国内外教学质量评估研究的发展与动态[J].中国劳动关系学院学报,1990,2:56-58.
[5]王彦雨.高校教学质量监控体系构建思考[J].合作经济与科技,2016,5:121-124.
[6]付惠.改革开放以来中国高校教师教学质量评价的研究(1978-2014年)[D].上海:华东师范大学,2015.
[7]韦丽娃,丛彬龙.基于学生表现的教师教学质量评价方法研究[J].沈阳航空航天大学学报,2017,34(05):92-96.
[8]袁琴.CIPP评价模式在高职项目课程评价中的应用[J].中国职业技术教育,2013(35):53-57.
[9]陈建兰,胡晓敏.基于教学质量评价的教学方法的探讨[J].教育教学论坛,2015,25:177-178.
[10]刘芳.教学质量评价的数学方法[J].安徽工业大学学报(社会科学版),2001,18(03):114-115.
[11]张大克,王玉杰,万丽丽.高校数学基础课教师教学质量评价方法的研究[J].大学数学,2014,30(06):43-46.
[12]苏为华.多指标综合评价理论与方法问题的研究[D].厦门:厦门大学,2000:80-83.
