基于ARIMA-SVM组合模型的中国出口欧盟食品安全风险预测

楼皓，曹倩，李海生

北京工商大学计算机与信息工程学院，食品安全大数据技术北京市重点实验室（北京 100048）

在经济全球化背景下，食品的流通贸易变得频繁，食品安全问题成为世界各国最关注的民生问题之一。由于食品安全受到多种复杂因素影响，中国每年出口欧盟的食品中，会有部分食品因不符合欧盟食品安全标准遭到欧盟食品及饲料快速预警系统（RASFF）通报。因此，加强中国出口食品的安全预测，有助于深度了解中国对外食品贸易走势，具有重要的长期实践意义[1-3]。

当前食品安全预测方法众多，传统预测方法基于数据是线性变化为前提，代表有差分自动回归移动平均（ARIMA）[4]，但不能准确地描述食品安全与其影响因子间的非线性关系，使用十分受限。近年来出现的神经网络、支持向量机（SVM）等技术却非常善于发掘非线性变化规律数据中存在的联系[5-6]。中国对外出口食品数据不仅具有一定周期性变化特点，同时也有相当一部分随机性特点。因此，单一模型对食品数据无法准确预测。 为了解决这个问题，提出一种基于ARIMA和SVM的食品安全预测模型。选择差分自动回归移动平均模型对食品数据的时间序列进行建模，采用支持向量机对差分自动回归移动平均的预测残差进行建模，两者结果相加以得到最终的食品安全预测结果。试验表明，基于ARIMA-SVM模型较单一模型有更高的预测精度，为今后食品安全预测问题提供建模工具[7]。

1 研究方法

1.1 差分自回归移动平均模型（ARIMA）

ARIMA是最典型的时间序列预测方法，拥有简单、短期预测效果良好的特点。ARIMA(p, d, q)模型由3部分组成，即自回归模型（Auto regression，AR），其中p为相应的回归项；单整阶数（Integration，I），d为差分阶数，用来得到平稳序列；移动平均模型（Moving average，MA），q为相应的移动平均项。时间序列模型要建立计量模型，需满足平稳性序列这一条件，若时间序列是非平稳序列，则要通过差分转换为平稳性序列。ARIMA(p, d, q)模型是把非平稳时间序列经d阶差分后得到平稳时间序列，构成ARMA(p,q)，其一般形式为式（1）。

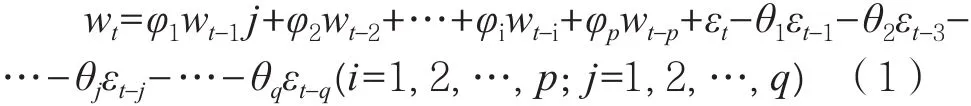
式中：wt表示平稳时间序列；εt表示白噪声；φi(i=1,2, …, p)表示{wt}的参数；θj(j=1, 2, …, q)表示{εt}的参数。将非平稳时间序列转化为平稳时间序列后，需要对平稳时间序列分别绘制其自相关系数ACF图和偏自相关系数PACF图，通过对图形的分析，得到最佳自回归阶层p和移动平均阶数q，模型参数φi和θj由阶数q确定。在最小信息量准则（AIC）和贝叶斯信息量准则（SIC）基础上进行模型确定。

式中：n表示模型中参数个数；L表示模型的极大似然函数。AIC和BIC准则的提出可有效弥补自相关图和片自相关图定阶的主观性，能在有限的阶数范围内更快找到最优拟合模型。

1.2 支持向量机模型（SVM）

支持向量机（SVM）的概念由Cortes和Vapnik于1995年第一次提出，基于统计学VC维理论和结构风险最小原理基础上提出，最初应用于模式的分类，其核心是通过核函数的引入，将低维空间中的非线性问题通过映射到高维度空间，进而转化为高维度中的线性凸二次规划问题。其优点是利用内积核函数代替高维空间的非线性映射，最终结果的决定取决于少数支持向量，计算复杂度只与支持向量的数目相关，与样本空间维度无关，某种意义上避免“维数灾难”，保证了解的唯一性和全局最优性，且算法简单，鲁棒性强。

由于SVM模型是用于线性不可分的预测残差进行分析，假设给定一个特征空间上的训练数据集T={(x1, y1), (x2, y2), …, (xN，yN)}，其中xi∈Rn，yi∈{+1, -1}，i=1, 2, …, N，引入松弛因子ξi≥0，对应的最优化问题如式（4）所示。

由最优w*和b*求得分离超平面，见式（5），进而确定分类决策函数，如式（6）所示。

支持向量机回归是支持向量机的扩展应用，其核心是ε-insensitive误差函数和核函数，定义松弛变量εi和基于ε不敏感损失函数的支持向量机回归模型如式（7）所示。

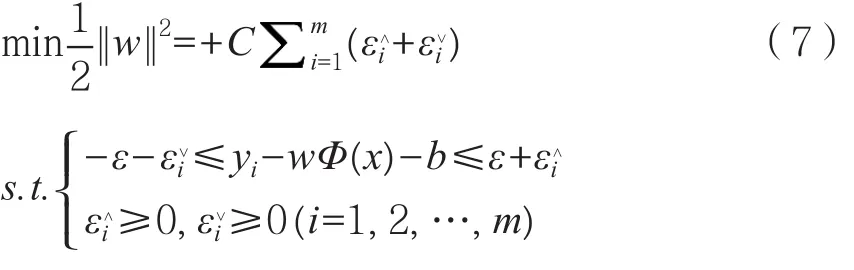
式中：εi和εi表示松弛变量，定义模型的误差范围；C表示正则化参数，其主要功能是对松弛变量和置信范围的度量优化。推导可得最终支持向量机回归函数。如式（8）所示。

对式（7）转化为等价的二次规划问题求解后可得αi*和αi，在KKT准则的基础上可求得偏差b。式中K(xi, yi)称为满足Mercer条件的任意对称函数，也即核函数，很大程度上决定模型性能的优良。经过分析可知，在采用交叉（CV）和网格寻优算法（GS）验证基础上，分别尝试各种常用的核函数，找出模型拟合效果最好误差最小的一种，在反复试验基础上，确定径向基函数（RBF）最符合试验要求[8]。

1.3 ARIMA-SVM组合预测模型基本思路和步骤

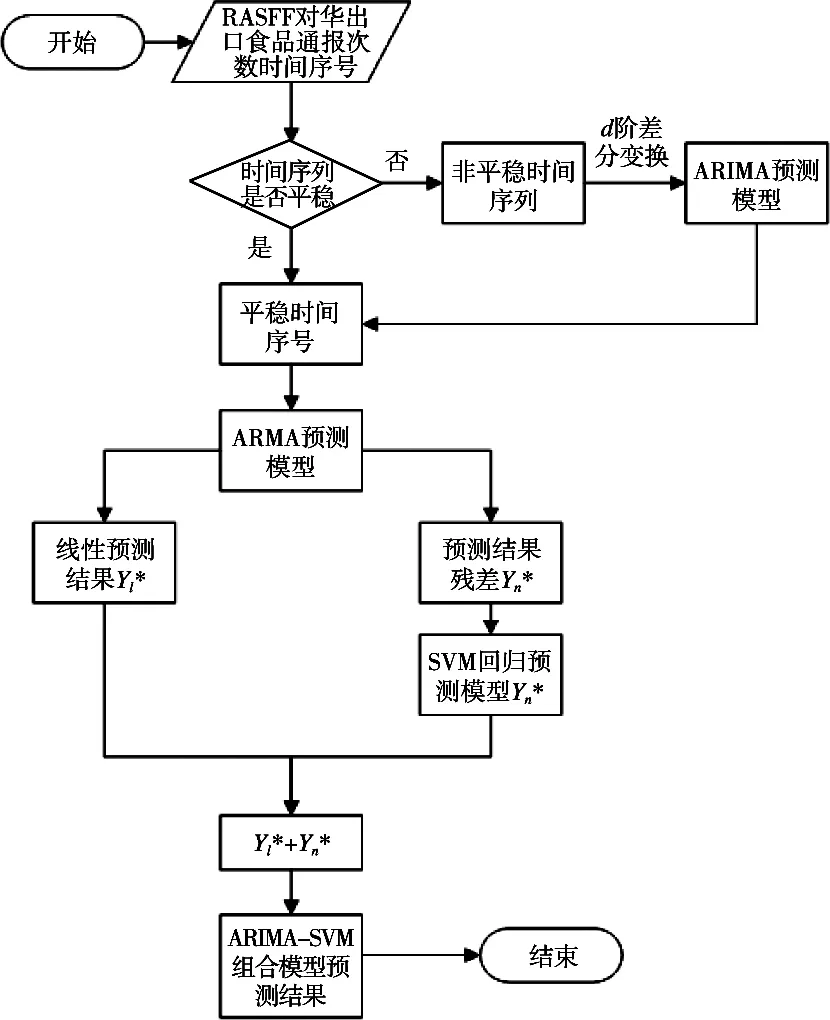
图1 组合预测模型流程图

中国出口欧盟食品安全受多种风险源因素的影响，因此，将中国出口欧盟不合格食品通报次数的时间序列Yt以月度分布构建时间序列，作为输入变量带入ARIMA模型进行预测，得到符合线性变化规律的结果Yl*，此时预测残差Yn=Yt-Yl*。因为预测残差Yn中包含时间序列的非线性部分，故使用SVM模型进行回归预测，将Yn作为支持向量机模型的输入变量得到预测结果Yn*。此时，通过单独的ARIMA模型和SVM模型分别得到预测值Yl*和Yn*，将两者相加即是ARIMASVM组合预测模型的最终预测结果Yt*=Yl*+Yn*[9-15]。组合预测模型建模步骤如图1所示。

2 仿真试验及预测分析

2.1 数据来源及模型评价指标

选取欧盟食品及饲料快速预警系统门户网站（RASFF）上2009年1月至2018年12月共计120个自然月的欧盟对华食品边境拒绝通报次数的时间序列作为研究对象，以前108个月的数据样本作为训练样本对模型进行构建，后12个月的数据样本作为测试样本。图2为2009年1月至2018年12月欧盟对华边境通报次数变化图。

图2 2009年1月至2018年12月欧盟对华食品出口边境通报次数变化图

为更直观评价ARIMA-SVM组合预测模型的预测效果，采用均方根误差（Root mean squared error，RMSE）和平均绝对误差（Mean absolute percent error，MAPE）作为评价指标，对模型的预测效果进行评估，均方根误差和平均绝对误差定义。

式中：xi表示实际值；表示预测值；n表示预测样本数量。

2.2 ARIMA模型线性预测

对2009年1月至2018年12月欧盟对华边境通报次数做月度序列图分析可知（图2），其呈缓慢上升的趋势，属于明显的非平稳时间序列，并存在较大波动，整个月度时间序列方差差别显著。以2017年12月为切点，将整个数据集分为两部分。以2009年1月至2017年12月的数据作为组合预测模型的建模数据，2018年1月至12月的数据作为验证数据，对通报次数进行预测进而评估模型的预测可靠性。

对原始数据时间序列进行一阶差分，相关试验的软硬件环境分别为EVIEWS 10，Windows 10教育版，2.6 GHz CPU、8 GB内存的笔记本电脑。原始时间序列经过一阶差分处理后如图3和图4所示。由图3可知，一阶差分均值基本维持在0左右，基本可以判断是稳定的时间序列。由图4时间序列ADF单位根检验可知，p-value小于0.05且检验值的绝对值均大于临界值的绝对值，拒绝原假设。故原始时间序列经一阶差分后变成了平稳时间序列。故确定ARIMA(p,d,q)模型中的d=1。

图3 一阶差分时间序列图

图4 一阶差分时间序列ADF检验图

一阶差分后残差自相关系数（ACF）和偏自相关系数（PACF）如图5所示，可知lag=12（滞后值）时，自相关系数滞后2阶后开始有衰减的趋势且系数都不为0，可视为2阶拖尾；偏自相关系数滞后2阶后也开始衰减且系数不为0，视为2阶拖尾。自相关和偏自相关均为拖尾，故适用AR（2）模型。

图5 残差自相关和偏自相关系数图

因此ARIMA模型阶数可初步定为ARIMA(1, 1,0)，ARIMA(2, 1, 0)，ARIMA(1, 1, 1)和ARIMA(2, 1,1)，利用Eviews软件分别对4个模型进行计算，根据最小信息量原则，最终确定最优模型为ARIMA(2, 1,1)，各ARIMA模型的AIC和SIC检验值如表1所示。

表1 差分自移动回归平均模型相关信息量检验值

预测结果及RASFF对华出口食品边境通报次数的残差值、观测值及拟合值的对比分别如图6和图7所示。ARIMA模型对RASFF对华食品边境通报次数1月至10月的预测趋势与实际值的趋势是非常接近的，但预测值只有在3，5，8和9月的预测值与实际值非常接近，其余各月预测值与实际值相差很大拟合效果不是很理想，仍有待进一步优化。

图6 差分自回归移动平均模型ARIMA(2, 1, 1)预测结果

图7 我国出口欧盟食品边境通报次数的残差值、观测值及拟合值的对比图

2.3 SVM模型非线性预测

模型ARIMA(2, 1, 1)残差包含非线性部分，故使用SVM模型对残差进行训练。试验采用MATLAB R2014b版本，调用Libsvm 3.23工具箱实现。SVM模型的2个重要参数分别为核函数和特征空间向量，经过多次试验分析，确定核函数选择径向基核函数（RBF），定义为：

确定SVM模型核函数使用径向基函数，在反复多次试验的基础上确定模型参数分别为C=53，σ=3.6，ε=0.01。根据参数对2018年1月至2018年12月RASFF对华出口食品边境通报次数进行预测，预测结果与实际结果对比图见图8。

SVM模型预测趋势在1-3，4-5，7-9及10-12月是符合实际值趋势的，与ARIMA模型相比略有不足。在预测值精准度上，SVM模型的预测值与实际值的差别幅度要大于ARIMA模型，仍有待优化。

图8 支持向量机模型预测值与实际值结果对比图

2.4 ARIMA-SVM组合模型预测及结果分析

在ARIMA(2, 1, 1)模型的预测值及残差部分SVM模型的预测值的基础上进行求和，得到ARIMA-SVM组合预测模型的预测值，将各模型对2018年1-12月RASFF对华食品出口边境通报次数的预测值进行对比，结果如图9所示。

由图9可知，ARIMA模型预测值在5-9月期间的预测值与实际值变化趋势相同，预测值与实际值相差不大。SVM模型在1-5月期间的预测值与实际值变化趋势相同，但预测值与实际值误差要大于ARIMA模型。单模型预测的情况下，ARIMA模型拟合精度要高于SVM模型。而ARIMA-SVM组合模型不论是数据变化趋势或是数据误差方面，均要优于任一单模型。因此单模型只适用于短期预测，长期预测使用组合预测模型效果更佳[16-19]。各模型预测结果及预测精度分别如表2和表3所示。

图9 2018年1-12月我国出口欧盟食品出口边境通报次数各模型预测结果对比图

表2 各模型预测结果

表3 各模型预测精度

不论是单独的ARIMA模型或是SVM模型，都不能兼顾捕捉到数据中存在的线性特征和非线性特征。组合模型的优势就在于分别保留ARIMA模型和SVM模型的优势部分，利用ARIMA模型对数据线性特征进行建模，利用SVM模型对数据的非线性特征进行建模，从而有效避免ARIMA模型对数据非线性特征处理的短板。表2和表3数据显示出组合模型相比较单一模型在预测结果和预测精度上有较为明显的优势，说明ARIMA-SVM组合预测模型对原始数据中隐藏的数据关系的认知上要比单一模型表现更佳，有效克服单一模型的局限性[20]。同时，试验结果验证组合预测模型对中国出口欧盟食品质量安全的预测结果是可靠的，对今后中国出口欧盟食品的质量起到有效监管作用。

3 结论

1) 一定时间节点内RASFF对华出口食品通报次数的时间序列是食品安全和数据关系的一种直观反映。基于挖掘食品安全相关数据的时间序列自身隐含信息的角度出发，建立ARIMA-SVM的时间序列组合预测模型。实证研究表明，基于2009年至2018年RASFF对华食品出口边境通报次数的数据，利用2018年1-12月的数据进行验证，结果表明不论是预测值或是预测精度，组合模型均优于单一模型。

2) ARIMA-SVM预测模型较单一预测模型短期内能够较为准确反映出中国出口欧盟食品的质量安全，对中国食品出口安全风险起到一个有效评估，但模型参数的选择、数据噪声等影响因子仍然会对组合模型的预测精度产生影响。此外，影响食品安全的不确定因素远颇多，也会在一定程度上影响预测的精度，导致预测精度下降。