平行声屏障的陷波模态及其插入损失优化

郭文成 叶 璇

0 引言

声屏障常见于高速公路、铁路和需要噪声控制的工厂等场所，一般安装在噪声源与噪声敏感区域之间，保证噪声敏感区域免受噪声的危害。直立型声屏障一般采用刚性材料制作，可以有效切断噪声的传播途径。然而，通过声屏障的边缘，尤其是顶端衍射到声影区的噪声却无法得到有效控制。提高声屏障的高度可以增加声影区的范围，改善低频插入损失。但是该方法造价较高，并且高度过高容易产生额外的结构安全问题，如抗横向荷载的能力变差，因此在实际应用中有较大局限性。

通过改变声屏障的形状以及顶端结构来改善其性能一直以来都是国内外学者研究的热点[1]。研究的对象包括但不限于T 型声屏障、Y 型声屏障以及具有吸声柱体、锯齿型和声扩散体等顶端结构的声屏障等[2−7]。在治理交通噪声时，声屏障往往是平行地布置在道路两侧，称之为平行声屏障。已有研究结果表明，声波在平行声屏障之间容易产生多次反射，使到达声影区的衍射声能增加，从而导致声屏障性能下降[8−9]。为了抑制平行声屏障之间的声波多次反射，可在声屏障内表面设置吸声材料吸收反射声能，然而目前广泛使用的离心玻璃棉等纤维吸声材料，在户外恶劣条件下使用时容易受潮、脱落和积聚粉尘，实际效果欠佳，同时还会带来潜在的环境污染问题，因此不适合作为声屏障的吸声材料使用。改变声屏障之间的内部声场分布也是一种有效的方法。有学者提出将声屏障向内倾斜10◦，使声波向地面反射，可降低一部分通过声屏障顶端的衍射声能[10]。Yang 等[11]采用有限元仿真分析的方法指出，平行声屏障之间的陷波模态是导致其性能下降的重要原因之一。当陷波模态处于共振频率时，平行声屏障之间形成驻波效应，此时声能最大并垂直地入射到声屏障的顶端，产生了最佳的衍射条件，导致插入损失减小。文中同时提出了一种楔形结构表面，较好地改善了平行声屏障的性能。类似的还有Wang 等[12]提出的一种具有不均匀阻抗表面的声屏障。

本文基于以上研究成果，采用有限元仿真的方法，对导致平行声屏障插入损失恶化的陷波模态特性进行了分析。采用经典的理论模型验证仿真模型的准确性。最后，从陷波模态的角度讨论了不同类型声屏障的插入损失优化效果。

1 有限元仿真模型

图1为平行声屏障布置在噪声源两侧的二维有限元仿真模型。模型中定义了两个声场区域，其一为计算声场区域，包括平行声屏障、地面、噪声源S和接收点R。为了简化计算模型，声屏障的高度设置为1 m，厚度为0.1 m。声屏障之间的距离为2 m，噪声源S布置在两个声屏障的正中央位置，接收点R与噪声源S之间的距离为5 m，除微穿孔板以外的其他表面均视为刚性边界。

其二为计算声场区域外部的完美匹配层(Perfectly matched layer, PML)[13]。该区域为自定义的声吸收层，可允许内部声场的声波传播进来而几乎没有反射，在有限大小的几何区域内模拟自由扩散的声场条件，有效地提高了模拟的运算速度。模型采用自由三角形进行有限网格化。为了保证计算的准确度，三角网格的尺寸不大于最高计算频率波长的1/6。本文的三角网格的尺寸最大值设定为0.014 m，可保证最高计算频率扩展至4000 Hz。

声屏障的插入损失(Insertion loss, IL)计算公式为

式(1)中，p0和p1分别为声屏障安装前后接收点R处的声压。

图1 平行声屏障的有限元仿真模型Fig.1 Finite element model of parallel barrier

为了验证有限元仿真模型的准确性，本文采用Kim 等[14]基于几何衍射理论提出的数值模型进行对比验证。图2为单侧声屏障的衍射模型。在柱面坐标系(r,θ,z)中，假定相对于声屏障顶点Q，声源点S和接收点R的径向距离和角度分别表示为(RS,θS)和(RR,θR)，Q点的角度为νπ。则衍射波在接收点R处的声场可表示为

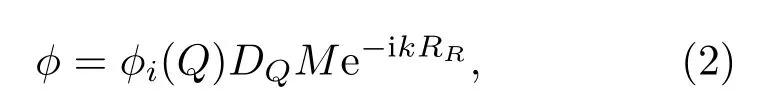
式(2)中，ϕi(Q)为Q点的入射波，DQ为衍射系数，M为比例因子。声波斜入射时，有

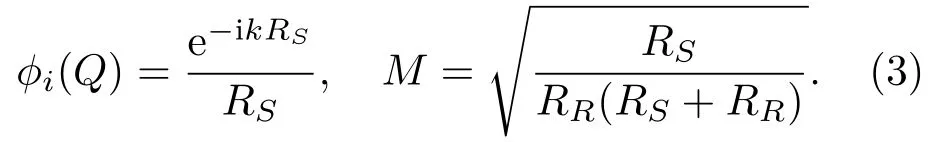
插入损失IL为

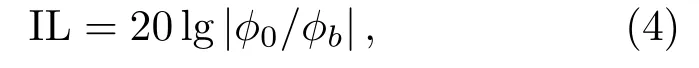
式(4)中，ϕ0和ϕb分别表示没有声屏障和有声屏障时的声场。

图2 单侧声屏障衍射模型Fig.2 Diffraction model of single barrier

图3 有限元仿真和Kim 模型预测的单侧声屏障插入损失对比Fig.3 Comparison of the insertion loss of a single barrier predicted by the proposed finite element model and Kim’s model

验证对象为简易单侧声屏障模型，其中声屏障的高度为2 m，噪声源高度为0.5 m，与声屏障的水平距离为2 m；接收点布置在声屏障另一侧并与噪声源的位置成镜像关系。计算的频率范围为10～4000 Hz，间隔10 Hz，计算结果如图3所示。可以看到有限元仿真模型的计算插入损失与Kim 模型计算的插入损失结果基本吻合，表明本文所采用的有限元仿真模型是准确可靠的。

2 陷波模态分析

为了说明单侧声屏障变化为平行声屏障之后的插入损失恶化现象，本节基于已验证的有限元仿真模型对两者的插入损失进行了模拟，结果如图4所示。可以看到随着频率的上升，单侧声屏障的插入损失也是逐渐上升的。原因之一是高频段声波的波长较短，衍射能力较差，在声屏障背后所形成的声影区也较小。而平行声屏障的插入损失曲线则随着频率的增加呈现显著的波动现象，峰谷不断交替，并且几乎整体在单侧声屏障的插入损失曲线之下，部分频率的插入损失甚至小于0。所以，当只需对噪声源一侧的敏感区域进行保护时，选择平行声屏障是不合时宜的。当需要对噪声源两侧的敏感区域进行保护时，又不得不选择平行声屏障，那么就必须将平行声屏障的插入损失恶化效应降低到最小。

图4 单侧声屏障和平行声屏障的插入损失对比Fig.4 Comparison of the insertion loss of a single barrier and parallel barrier

事实上，平行声屏障与地面形成了一个三面闭合的顶端开口结构，这个顶端开口的结构存在本征模态(即陷波模态)。陷波模态的共振频率(也称本征频率、固有频率等)与声屏障的几何边界条件有关。为了说明陷波模态与平行声屏障插入损失的关系，此处选取了图4中4 个插入损失曲线的波谷频率，即180 Hz、350 Hz、520 Hz 和690 Hz 频率处的声场分布进行了分析，如图5所示。可以看到这4个频率处的声场均出现了明显的简正模式，声波的传播处于驻波状态，方向与平行声屏障垂直。绝大多数的声能被限制在顶端开口的结构内，极小部分的声能扩散到外部空间。这大部分的声能垂直地入射到声屏障顶端。根据几何衍射理论可知，对本文的研究对象而言，垂直入射声波的衍射系数最大[15]。因此平行声屏障的陷波模态处于共振频率时，接收点的衍射声能达到极大值，插入损失取得极小值。

一般来说，平行声屏障的陷波模态共振频率可由几何条件相同的闭合结构的共振频率计算公式进行预估，公式如下所示：

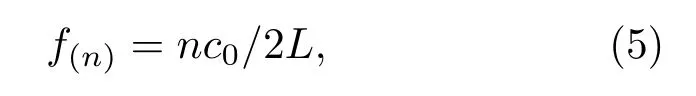
图5 平行声屏障的各阶陷波模态Fig.5 Wave-trapping modes of parallel barrier

式(5)中，f(n)表示第n阶陷波模态的共振频率，c0为声音传播的速度，L为声屏障的间距。上文中所述的4 个频率分别为平行声屏障的第2、第4、第6和第8 阶陷波模态共振频率。为了验证计算公式的准确性，表1列出了仿真模拟和公式计算的陷波模态共振频率对比。结果表明，两组数据之间的偏差极小，意味着在确定了平行声屏障之间的几何条件之后，可以快速准确地通过公式对声屏障陷波模态的共振频率进行计算，并提前采取控制措施。

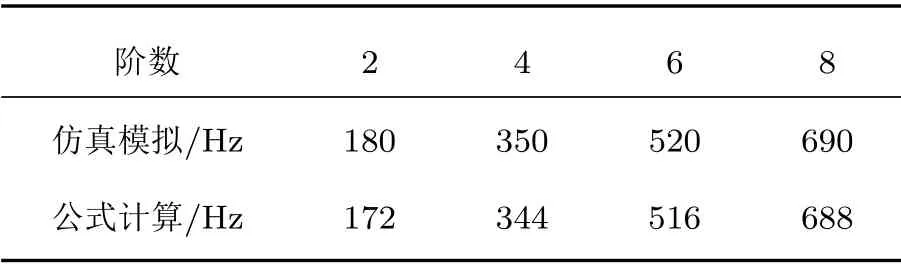
表1 陷波模态的共振频率对比Table 1 Comparison of the resonance frequencies of wave-trapping modes

3 插入损失优化

本节对3 种可能改善平行声屏障插入损失的优化方法进行了仿真分析。声屏障的构造如图6所示，包括内表面带楔形结构的声屏障、内表面带扩散型声屏障和吸声型声屏障。其中，单个楔形结构的高度为0.25 m，向下倾角为60◦。扩散型结构按照二次余数扩散体[16]进行设计，所选为7 阶扩散体，深度比值为0 :1 :4 :2 :2 :4 :1，最大深度为0.019 m，对应的设计频率为520 Hz(即平行声屏障的第4 阶陷波模态)，单个空腔的宽度为0.025 m。吸声型声屏障采用的是绿色环保的无纤维吸声体--微穿孔板吸声体，吸声体板厚为0.4 mm，穿孔直径为0.3 mm，穿孔率为1%；其吸声系数采用马大猷院士[17]提出的经典理论公式进行计算，结果如图7所示，吸声系数的峰值设计在520 Hz，达到了0.996。

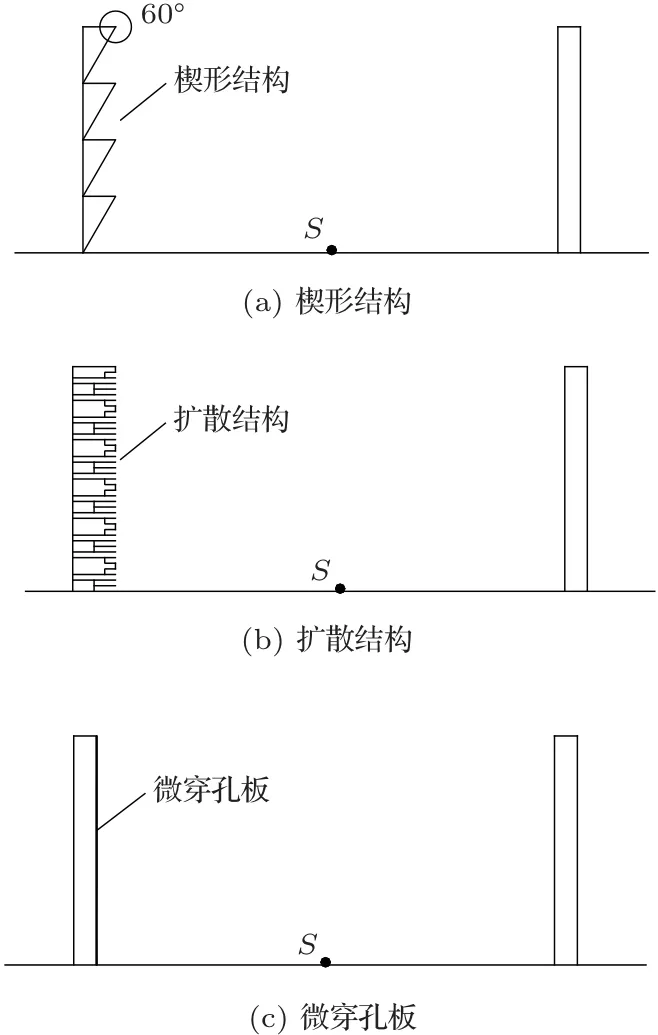
图6 3 种不同形式的平行声屏障Fig.6 Three types of parallel barriers

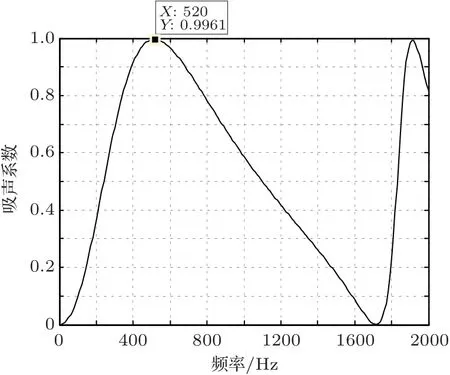
图7 吸声型声屏障的吸声系数Fig.7 Sound absorption coefficients of absorptive barrier

图8为采用有限元仿真模型计算得到的单频插入损失对比，图9则是基于声压级叠加原理[18]计算得到的1/3倍频程中心频率处的等效插入损失对比。为了方便分析，图中只展示了250～1000 Hz 两个倍频程范围的结果。从图中可以看出，3种不同结构声屏障的插入损失相比刚性平行声屏障而言均有不同程度的提升。提升效果最显著的是吸声系数经过优化设计的吸声型声屏障；单频插入损失提升最大值来自于具有楔形结构的声屏障，在460 Hz 处的插入损失提升了将近23 dB。而对于具有扩散结构的声屏障来说，虽然理论上它的异型结构可以降低平行声屏障之间的多次反射效应，但是实际获得的插入损失优化效果并不理想。除了在其设计频率520 Hz 处取得了17 dB 的提升外，其余频率的插入损失几乎和楔形结构相当。值得注意的是，吸声型声屏障的插入损失曲线的波动是最小的，尤其是在400～700 Hz 这个微穿孔板吸声体吸声系数较大的频率范围。主要原因在于，吸声材料将平行声屏障内原本被陷波模态锁住的声能量大幅吸收，同时吸声边界改变了原有的刚性边界条件，使陷波模态发生了变化，从而提高了插入损失。从图8和图9的结果对比还可以发现，楔形结构和扩散结构可以显著提升某一个单频处的插入损失，这在某些具有特殊声学需求的场所可能会得到较好的应用。而如果想改善声屏障在某个倍频程范围内的等效插入损失，那么提高该频段的吸声系数是更好的选择。

图8 不同平行声屏障的插入损失对比Fig.8 Comparison of the insertion losses of different parallel barriers

图9 不同平行声屏障在1/3 倍频程中心频率处的插入损失对比Fig.9 Comparison of the insertion losses of different parallel barriers in one-third octave band center frequencies

4 结论

当单侧声屏障变化为平行声屏障后，由于内部声场多次反射以及陷波模态的存在，使其插入损失显著下降。为了解决该问题，本文基于有限元仿真模型对平行声屏障的陷波模态和插入损失优化方法进行了研究。有限元仿真模型的准确性经过理论模型的验证，可准确预测插入损失。文中还对3种结构的平行声屏障进行了仿真分析。结果表明，相对于平行刚性声屏障而言，吸声结构在250～1000 Hz范围内的1/3倍频程中心频率处的插入损失算术平均值最大，达到了6.6 dB，因为吸声结构有效地抑制了陷波模态。而扩散结构和楔形结构的插入损失算术平均值较小，分别为1.6 dB 和1.1 dB。原因在于它们在陷波模态附近的插入损失优化效果不佳，甚至产生了恶化的现象。因此，处理好陷波模态附近的插入损失对于优化整个声屏障的隔声性能来说至关重要。