风力机叶片气动噪声的影响参数∗

曾明伍 朱卫军 孙振业 郑大周 李松林

0 引言

我国风电产业保持高速发展，2018年新增风电并网装机容量高达2059×104kW，累计并网装机容量1.84×108kW，全年风电发电量3660×108kW·h[1]。随着人们在低风速区大规模开发建设风电场，风力机越来越靠近城镇、港口等人口密集地区，甚至分散式布置于人口密集区，风力机运转产生的噪声与人类日常生活的矛盾日益显现。风力发电机组发出的噪声会刺激人耳的前庭系统，引起耳鸣、睡眠障碍等症状，这种现象被称之为“风电场综合症”[2]。因此，控制并降低风电机组的噪声非常必要，如果不采取措施积极对待，则会阻碍风电产业的发展。风力发电机组的噪声主要包括机械噪声和气动噪声[3]，机械噪声主要是由机舱内机械设备的振动产生，可以通过提高加工工艺、安装精度等方法加以控制；气动噪声由气流与叶片相互作用产生，包含低频噪声、湍流入流噪声、翼型自噪声[4]。国内外一些学者利用风洞试验和数值模拟对风力机气动噪声展开研究，Shen等[5]将可压缩纳维-斯托克斯(Navier-Stokes, NS)方程分离成不可压缩流动方程和无黏声学方程，提高了仿真效率。Zhu 等[6]采用大涡模拟(Large eddy stimulation, LES)和FW-H声比拟方法对带尾缘锯齿的翼型段进行气动及气动声学仿真，调研了不同功角、锯齿长度、尾缘锯齿安装角、尾缘锯齿波长比的翼型的噪声水平，发现较小的尾缘锯齿波长比、负值的尾缘锯齿安装角降噪能力更强。任旺等[7]采用LES方法计算DU91-W2-250 翼型的流场，利用FW-H方法求解远场噪声分布，研究了3 种翼型尾缘厚度(相对于弦长分别为0%、1.2%、2%)对噪声的影响，发现2%和0%尾缘厚度均降低了声压级，尤其是在1500 Hz以上的高频部分。相较于原始翼型，在监测点R1处，2%尾缘厚度噪声下降8 dB，0%尾缘厚度下降约10 dB；在监测点R2处，2% 尾缘厚度下降7.5 dB，0%尾缘厚度下降约9.3 dB。该文指明翼型的噪声声压级水平和尾缘涡量的脱落密度、涡核能量密度密切相关，2%和0%尾缘厚度使得尾缘部分的表面脉动压力频率下降，导致了较低的噪声水平。郭茂丰等[8]考虑风力机叶片与空气的流固耦合作用，基于ANSYS workbench工作平台，采用双向流固耦合方法，预测风力机的气动噪声，并与额定工况下的实验数据对比。

本文选取基于NACA、DU 翼型的某风力机叶片作为研究对象，针对翼型族、叶片几何参数、整机参数、来流情况等因素，采用扬州大学开发的风力机翼型及风轮气动噪声计算软件计算噪声水平，该软件采用修正BPM 模型分别计算翼型、叶片的气动噪声，对水平轴风力机叶片气动噪声的影响参数展开研究。

1 风力机叶片气动噪声预测模型

根据风力机叶片气动噪声产生机理，低频噪声是由于塔影效应、风剪切效应和尾流效应等引起的来流速度的变化，使叶片与周期性来流相互作用产生压力脉动，形成周期性的、频率为叶片通过频率整数倍的离散噪声，人耳对低频噪声不敏感。来流湍流噪声是一种宽带噪声，它是由于叶片与来流湍流相互作用产生涡旋而引起的，来流湍流噪声与叶片转速、翼型剖面和湍流强度有关[9]。翼型自身噪声主要是宽带噪声及声调噪声，包括尾缘噪声、失速噪声、钝尾缘噪声、叶尖噪声、层流涡噪声，主要由翼型边界层和翼型本身作用产生，主要包括[10]：

(1)尾缘噪声：由湍流边界层与叶片尾缘相互作用形成，其频率范围在750～2000 Hz，是风力机叶片主要的高频噪声。

(2)失速或分离噪声：当攻角较大时边界层会发生分离，吸力面的湍流涡变大，当湍流涡变成尾迹时产生分离流噪声。随着攻角增大到一定程度时，边界层发生大规模分离，翼型完全失速，湍流涡的尺度变得非常大，产生失速噪声。

(3)钝尾缘噪声：当尾缘厚度增大到一定程度时，叶片尾缘会脱落出涡，产生卡门涡街，从而在叶片尾缘上下表面产生周期振荡载荷，形成离散的钝尾缘噪声，该噪声频率依赖于叶片尾缘形状、厚度和雷诺数，可以通过合理设计尾缘形状及厚度来降低。

(4)叶尖噪声：由于三维流动效应，在叶尖会形成叶尖涡，叶尖涡与叶尖相互作用产生叶尖涡噪声，其产生机理类似于尾缘噪声。叶尖涡噪声与叶尖的几何形状有很大的关系，如果叶尖呈方形且比较厚，则通常噪声会比较大。

(5)层流涡噪声：层流涡噪声是由叶片表面的缝隙和空穴引起的层流涡形成的噪声，是一种声调噪声。当层流边界层的大部分至少存在于翼型的一个面时，就会产生涡脱噪声，涡脱噪声主要是由尾缘的涡脱落以及起源于尾缘上游层流边界层的不稳定波动循环流动引起的。层流涡噪声是一种离散噪声，对大型风力机来说可以忽略。

美国可再生能源实验室的Brooks、Pope 和Marcolini 提出了用于风力机翼型的半经验噪声预测模型[11]， 该模型(简称为BPM 模型)对NACA0012 翼型(弦长不同)进行大量的气动和声学测量，包含5 种风力机叶片翼型自噪声半经验模型[12]。在无大分离流动时，该模型的计算速度和精度基本可以满足工程需要，但是由于受翼型几何参数、来流情况的影响，采用同一公式计算不同翼型的边界层参数会出现一定偏差。基于该模型，Lowson[13]改进了边界层参数计算，Moriarty等[14]也对半经验预测方法进行了改进。Zhu 等[15]和Leloudas 等[16]基于半经验预测模型，采用了带有新叶尖修正的叶素动量理论(Blade element momentum, BEM)模型，考虑了风剪切、塔影效应、湍流强度和湍流长度尺度对不同叶片截面的影响，建立了风力机翼型及叶片气动噪声预测模型，并与Bonus 300 kW 实验风机进行对比，验证了模型对风力机噪声源的仿真能力。除此以外，柏宝红等[17]发现传统BPM 半经验预测公式高估了压力面声源，进而将压力面与吸力面的声源噪声辐射的幅值比与边界层位移厚度的关系做了修改，由原来的一次方关系改进为二次方，采用改进后的公式对NACA0012 及较厚的风力机专用翼型DU-96-W-180进行仿真，结果表明进后的模型具有较高精度。

将叶片离散为有限个叶素，对每个叶素采用修正BPM 模型计算翼型自噪声，该模型可适用于不同翼型、不同工况，更适用于风力机叶片气动噪声预测工程领域。将所有叶素进行噪声叠加，得到叶片总气动噪声源，见式(1)和式(2)：

其中：LiTotal为第i个叶素的噪声源；SPLj为不同类型的噪声源；KA为A 加权值；LTotal为叶片的总噪声源，由所有叶素的噪声源叠加得到[15]。

风力机叶片气动噪声不同于风洞中相对理想状况下的翼型气动噪声，实际运行中受到湍流来流作用和风切作用，因此必须将BEM 方法与翼型噪声机理单向耦合。除翼型自噪声以外，在湍流来流作用下还会产生湍流来流噪声，见式(3)，各参数请参考文献[15]。

图1表示三叶片风力机采用BEM 求解每个叶素的相对来流速度与入流攻角，每个位置对应不同的流速、马赫数、攻角、边界层厚度、扭角、弦长等翼型参数，是翼型自噪声计算的必要输入参数[18]。输入弦长、扭角、相对厚度、尾缘钝度等叶片几何外形参数，以及来流风速、来流风向、来流的湍流度大小、偏航、仰角等整机参数，计算风力机叶片总气动噪声源。风力机叶片气动噪声传播受多种影响因素，包括声波扩展、传播距离、大气吸收、温度、地形等因素，噪声衰减公式如下：

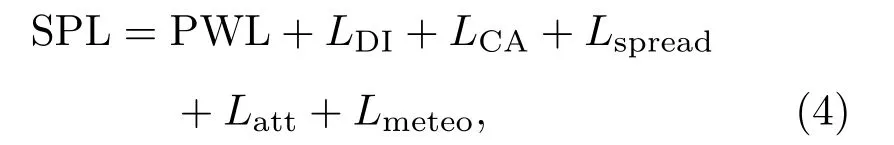
图1 翼型噪声机理与BEM 结合示意图[18]Fig.1 Schematic diagram of combination of airfoil aerodynamic noise mechanism and BEM theory[18]

其中：SPL，声压级，dB；PWL，噪声源声功率级，dB；LDI，噪声直接传播，dB；LCA，噪声对流放大，dB；Lspread，噪声几何扩散衰减，dB；Latt，空气衰减影响，dB；Lmetro，折射和地面影响，dB。

2 气动噪声的影响参数

本文选取某5 MW 海上风电机组作为参考模型，叶片基于NACA、DU 等翼型，叶尖区域采用DU21、CQUS180、NACA等翼型，其余区域采用DU系列翼型。风速为10 m/s，空气密度为1.225 kg/m3，黏性系数为0.000015 Pa·S，湍流尺度100 m，湍流强度0.05，观察者在与风力机下游位置对齐水平距离300 m 处。风力机额定转速取12.8 r/min，风切变指数取0.15，仰角、偏航角和锥角均为0◦，塔筒顶部直径2 m，底部直径3 m，塔筒高度88 m。本文采用扬州大学开发的风力机翼型及风轮气动噪声计算软件计算噪声水平，下文的翼型噪声计算结果考虑了尾缘噪声、分离噪声、钝尾缘噪声，不考虑湍流入流噪声、叶尖噪声和层流涡噪声；下文的叶片噪声计算结果考虑了尾缘噪声、分离噪声、钝尾缘噪声、叶尖噪声、湍流入流噪声和层流涡噪声。

2.1 翼型族的影响

翼型自噪声是风力机叶片气动噪声的最主要组成部分，因此翼型族的选取不仅决定了叶片气动性能的好坏，也影响气动噪声。翼型的几何参数主要包括尾缘厚度、相对厚度、最大弯度、前缘半径、尾缘角度等，本文主要研究不同尾缘厚度的翼型族对叶片气动噪声的影响。

目前风力机叶片一般基于NACA、DU 翼型设计，叶尖区域采用DU或NACA薄翼型，叶根区域采用基于DU 翼型改进的钝尾缘翼型。本文选择4 种尾缘厚度的翼型族设计叶片气动外形，分别计算叶片气动噪声，计算结果见表1。结果显示，尖尾缘叶片比钝尾缘叶片产生的声压级要低，随着叶片尾缘厚度的增加，风力机产生的气动噪声增大。但当尾缘厚度超过一定值后，气动噪声出现减小趋势，但始终大于尖尾缘叶片产生的噪声，与文献[7]的结论相符。这可能是由于尾缘厚度增加的修型，导致尾缘部分的表面脉动压力频率下降，当然还需要做进一步的验证，不属于本文的主要研究范畴。基于参考叶片的翼型分布，依次替换部分翼型，研究不同翼型选取对叶片气动噪声的影响，计算结果见表2。结果显示，叶尖区域的噪声是叶片气动噪声的主要部分，叶根区域翼型的选取对叶片气动噪声的影响较小。

表1 不同尾缘厚度分布下叶片的气动噪声对比Table 1 Comparison of aerodynamic noise of blades with different trailing edge thickness

表2 采用不同翼型族叶片的气动噪声对比Table 2 Comparison of aerodynamic noise of blades with different airfoil families

2.2 弦长的影响

由于叶片气动噪声由叶素噪声合成得到，因此弦长对叶片气动噪声的影响最终体现为弦长对翼型噪声的影响。本文选取DU30 作为参考翼型，研究不同弦长对翼型噪声的影响，固定攻角为5◦，入流合成速度分别取80 m/s 和40 m/s，尾缘厚度默认值为0.001 m。翼型DU30 截面段的弦长分别取0.25 m、0.5 m、1 m、1.5 m、5 m 五种不同数值，计算结果见表3和图2～图6。

表3 不同弦长下DU30 翼型的气动噪声对比Table 3 Comparison of aerodynamic noise of DU30 airfoil with different chord length

从噪声频谱图可以看出，在不同入流速度下，翼型吸力面、压力面尾缘噪声和边界层分离噪声随着弦长增加依次向低频段方向移动，即低频段噪声增加，高频段噪声减小，总声压级最大值由频率高向频率低移动。80 m/s 流速下的翼型的声压级比40 m/s 流速下的翼型的声压级高一个量级，0.25 m弦长的翼型在40 m/s 风速下和0.5 m 弦长的翼型在80 m/s 风速下的最大声压级所在频谱线的位置相同，0.5 m 弦长的翼型在40 m/s 风速下和1 m 弦长的翼型在80 m/s风速下也有相同规律，即风速变大，弦长变大，最高频位置不变。结果表明，在不同入流速度下，翼型的噪声随着弦长的增加而增加，且入流速度越大，噪声越大。

图2 弦长为0.25 m 的翼型DU30 在不同入流速度时的声压级Fig.2 Sound pressure level for DU30 airfoil with chord length 0.25 m at different wind velocity

图3 弦长为0.5 m 的翼型DU30 在不同入流速度时的声压级Fig.3 Sound pressure level for DU30 airfoil with chord length 0.5 m at different wind velocity

图4 弦长为1 m 的翼型DU30 在不同入流速度时的声压级Fig.4 Sound pressure level for DU30 airfoil with chord length 1 m at different wind velocity

图5 弦长为1.5 m 的翼型DU30 在不同入流速度时的声压级Fig.5 Sound pressure level for DU30 airfoil with chord length 1.5 m at different wind velocity

图6 弦长为2 m 的翼型DU30 在不同入流速度时的声压级Fig.6 Sound pressure level for DU30 airfoil with chord length 2 m at different wind velocity

2.3 风速、转速、桨距角的影响

设定某5 MW海上风电机组在风速3～25 m/s范围内运行，风轮转速随着风速的增加而增大，当风力机达到额定转速时达到额定功率。继续增大风速，转速不变，调节桨距角，使输出功率维持在额定功率附近不变，计算结果见表4。

表4 不同工况下机组气动噪声对比Table 4 Comparison of aerodynamic noise for different operating condition

结果显示在风速从3～25 m/s 范围内风力机正常运行过程中，风速增加，转速增加，此时风力机噪声变大。当风轮转速达到额定转速附近时，产生的噪声最大，风速继续增加，转速保持不变，桨距角增大，风力机噪声减小。因此，为了降低风力机的噪声水平，需要对风力机的变桨控制策略做精心设计，例如针对特定机位采取提前变桨措施。

2.4 风切变指数的影响

风切变指数的大小反映风速随高度增加得快慢，一般风切变指数在0.1～0.25 之间，本文改变风切变指数，观察气动噪声变化规律。计算结果见表5。结果显示，随着风切变指数的增加，噪声源的声压级总体呈上升趋势，不过变化范围较小，总体来讲风切变指数对风力机气动噪声影响不大。

2.5 来流风向的影响

风力机在运行过程中，当风向的位置改变时，为了捕获最大的风能，需要风力机快速地捕捉风向而进行偏航动作。本文假设当观察者在风力机正前方时，风力机以顺时针方向旋转，若风从右侧吹向风力机，则风向为正值，若风从左侧吹向风力机，则风向为负值，反之亦然，分别计算不同风向下风力机的气动噪声，计算结果见表6。结果显示，当风向从正对风力机到向两边移动时，噪声逐渐减小。在风向-20◦～20◦范围内，右侧风产生的噪声更大，其余风向范围内左侧风产生的噪声更大。

2.6 仰角的影响

为了避免风轮和塔架的碰撞，风电机组主轴具有一定仰角。本文假定机组主轴向上突出时，角度为正，反之为负，默认一只叶片方位角为0◦竖直向上时，其余两只叶片相隔120◦摆放。由于受风剪切影响，1 号叶片的声压级较其他两只更大，但不同的仰角会对风力机的总气动噪声产生影响，计算结果见表7。结果显示，风力机仰角增大，1号叶片离观察者距离减小，使得观察者位置的气动噪声越大，但增长速度渐缓。

表5 不同风切变指数下机组气动噪声对比Table 5 Comparison of aerodynamic noise for different wind shear

表6 不同风向下机组气动噪声对比Table 6 Comparison of aerodynamic noise for different wind direction

表7 不同仰角下机组气动噪声对比Table 7 Comparison of aerodynamic noise for different tilt angle of wind turbine

3 结论

本文以基于NACA、DU 翼型的某风力机叶片为研究对象，采用XFOIL 和修正的BPM 半经验模型分析风力机叶片的气动噪声特性，得出以下结论：

(1)翼型族的选取对风力机叶片气动噪声有较大影响，尖尾缘叶片比钝尾缘叶片产生的气动噪声小。随着叶片尾缘厚度增加，风力机的气动噪声增大。但当尾缘厚度超过一定值后，气动噪声出现减小趋势，但始终大于尖尾缘叶片产生的噪声。叶尖区域产生的噪声是整个叶片气动噪声的主要部分，叶根区域翼型的选取对叶片气动噪声的影响较小，因此叶片气动外形设计过程中，必须合理选择翼型族，才能有效控制叶片气动噪声。

(2)在不同入流速度下，叶片气动噪声随着弦长的增加而增加，入流速度越大噪声越大。

(3)风力机气动噪声随风速、转速增加而变大，当风轮转速达到额定转速附近时气动噪声最大，随着叶片桨距角增大，风力机气动噪声减小。因此为了降低风力机噪声水平，必要时针对特定机位可采取提前变桨控制策略。

(4)风切变指数增大，风力机噪声源的声压级总体呈上升趋势。当风向从正对风力机向两边移动时，气动噪声逐渐减小。在风向-20◦～20◦范围内，右侧风产生的噪声更大，其余风向范围内左侧风产生的噪声更大。风力机仰角越大，观察者位置气动噪声越大，但增长速度逐步变缓。