浅海单矢量传感器宽带声源三维定位仿真∗

于梦枭 周士弘

0 引言

浅海声源被动定位一直是水声学领域中的研究热点，而声源定位通常需要解决方位、距离及深度的三维参数估计问题。对于传统标量水听器，只有组成水平直线阵等阵列才能进行方位估计。现有研究中，对于距离及深度参数估计方法已有很多，匹配场处理属于其中比较传统的方法。Bucker[1]最早使用匹配场处理对距离与深度进行估计。Preisig[2]优化了因环境特性不确定而导致的匹配场处理方法性能下降问题。但方法对环境失配的敏感性及较大的计算量，限制了匹配场处理方法的实用性。生雪莉等[3]基于时间反转技术，利用垂直阵对声源距离进行估计。Yang[4]同样利用垂直阵分解简正模后，利用实测声场与拷贝声场的相关计算对声源距离及深度进行二维估计。而针对声源深度单独估计的研究中，Shang[5]利用垂直阵结合模态滤波技术，获得各阶简正模本征函数及距离所对应的相位信息后估计声源深度。李鹏等[6]使用水平阵，将信号变换到模态域进行处理，匹配各阶简正模的模态强度，与拷贝声场比对估计声源深度。郭晓乐等[7]消除简正模频散效应后分离简正模，利用波导不变量与水平波数差值之间的关系获得声源深度。

上述工作大多是针对水平或垂直基阵展开的，对于单水听器应用情况，戚聿波等[8−10]利用简正模相干项特征频率不变性特征，提出了基于自相关函数warping 变换及一种频域β-warping 算子的声源距离匹配估计方法。进一步地，于梦枭等[11]还提出了利用单水听器接收信号中多阶简正模相干项能量与非相干项能量比值的特征匹配定深方法。方法易于实现，但需要借助引导声源或拷贝声场模型。王文博等[12]基于声场干涉现象，提出了一种利用波导不变量的单水听器测距方法。

相比于传统声压水听器，由声压和三维振速分量组成的矢量传感器[13−20]不仅可以用来进行声源测向，还可以利用各阶简正模在不同径向速度下的水平波数计算值与假定值的线性比例关系，给出运动声源的径向速度，进一步结合上述单水听器被动定位的物理思想及方法，即可解决不依赖于拷贝声场模型或引导声源的测距问题，并以声源距离为已知量估计声源深度，从而实现声源的三维定位。本文对此进行理论仿真研究。

1 矢量声场基本理论

根据简正模理论，浅海波导中远程传播的声压场可表示为

式(1)中，S(f)为声源的频谱，um(·)为第m阶简正模本征函数(关于深度的实函数)，krm是第m阶简正模的水平波数，M为简正模数目，r为声源到接收器的距离，zr为接收深度，zs为声源深度，ρ(zs)为声源处的海水介质密度，f为频率。

对于频率为f的简谐波，质点振速与声压满足如下关系式：

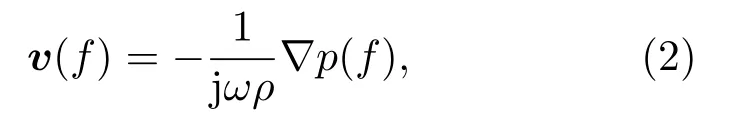
其中，ω= 2πf。在直角坐标系中， 式(2)中∇(·)=∂(·)/∂xi+∂(·)/∂yj+∂(·)/∂zk为梯度算子。若在柱坐标系中，∇(·)=∂(·)/∂ri+∂(·)/∂zk。i、j及k为各方向上的单位向量。水平方向振速vr与x方向振速vx及y方向振速vy之间关系满足式(3)：

其中，θ为信号水平方位角。

由式(2)可得，在柱坐标系下，水平振速vr和垂直振速vz的表达式分别为

式(5)中，u′m(zr)=∂um(zr)/∂zr为第m阶本征函数对深度方向的导数。

复声强频域上表示为声压与质点振速的共轭相乘即，包含实部与虚部两个部分，实部为有功声强，表示声场中传播的声能；虚部为无功声强，表示不传播的声能。水平复声强及垂直复声强的表达式如下：

其中，D(f)=-|S(f)|2/ωρ38πr，∆krmn=krm -krn，“*”为复共轭算符。

2 三维定位方法

2.1 声源方位估计方法

对于传统标量单水听器，因接收的声压信息无指向性，无法完成目标方位估计，需组成某种接收阵列后通过阵列信号处理方法得到方位谱，从而获得目标方位。而矢量传感器中，质点振速为矢量，带有方向信息，利用水平振速在正交方向上分量的三角函数关系可以估计方位。矢量方位估计方法主要包括平均声强器法、加权直方图法和直方图法等，本文仅考虑声场中存在一个目标，选取平均声强器方法对声源方位进行估计，若为多目标可选取其他方法。

根据式(3)，通过水平振速在x方向与y方向上的分量之间的关系可以获得方位信息。将声压与x、y方向振速分量组合为复声强，分别为

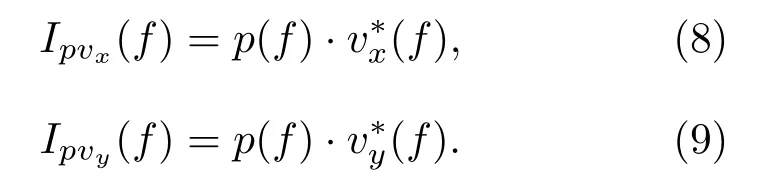
声源相对于单矢量传感器的方位角即为

其中，Re代表实部。

2.2 声源距离估计方法

利用单标量水听器测距方法较多，但往往需要利用拷贝场进行匹配测量或者使用引导声源作为参考。本文在测距方面选用基于自相关函数的相干项特征频率不变性的匹配测距方法，该方法需声场中存在引导声源或使用拷贝场，并且需已知声源深度或深度范围，这增加了方法实现的难度或整体计算量。同时，该方法需要将信号自相关函数中的非相干项部分置零，仅对相干项进行处理，在选择置零点时可能会引入人为误差。

本节简要介绍测距方法原理，当声源相对径向速度已知时，方法可以直接测距，无需引导声源或拷贝场或预知声源深度。当相对径向速度未知时，利用一种利用单矢量传感器的匀速运动宽带声源测速方法获得相对速度。在标量场的测距处理中，由于自相关函数中非相干项的存在，归一化处理后的时延谱图中，各相干项的时延轨迹可能变得模糊，从而影响距离估计的准确性，故Qi 等[10]对此方法进行改进，结合矢量声场理论，对垂直复声强的实部进行β-warping 变换后匹配测距，避免了去除非相干项可能导致的误差。假定各时刻声源在矢量传感器测得的方位角附近运动，方位变化较小，即假定各时刻声源相对径向运动速度近似不变，垂直复声强的实部与虚部分别表示为

垂直复声强的实部中不含有非相干项。将其实部时间序列向右移动一定时长，长度为信号的到达时间tr，利用时域算子对其进行warping变换[21]，若声源距离为r0，则某假定距离r下的相干项特征频率为[8]

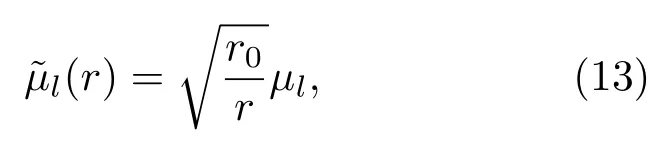
式(13)中，µl为真实距离下的各相干项特征频率。定义代价函数，将实测声场中相干项warping 变换后的归一化频谱与拷贝声场进行相关计算，当实测声场中各相干项特征频率与拷贝声场中相同时，代价函数值最大，其对应的距离即为估计距离。但该方法的实现需有一个重要前提，即声源深度需提前预知，否则实测声场与拷贝声场中各相干项间的归一化能量关系不一致，会导致方法失效。

若已知声源相对径向速度后，可以解决声源深度未知的问题，同时估测距离时不再需要拷贝场，可以减小计算量。选择时间点已知的L个信号，假定该段信号的初始距离后，对垂直复声强实部进行warping变换处理。根据式(13)，仅需利用某两阶的相干项信息即可进行距离估计，若初始距离准确，则每一时刻的距离都与实际距离相同，不同时刻下的相干项特征频率始终相等；若初始距离设定不准确，则每一时刻下的假定距离与真实距离的比值也不尽相同，故不同时刻的相干项特征频率始终在变化。定义代价函数

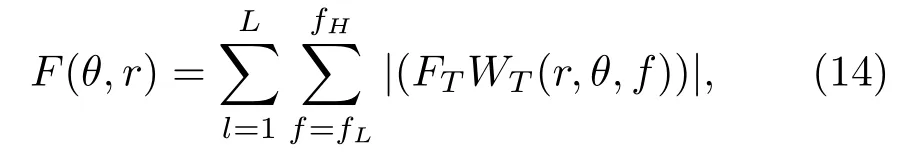
式(14)中，FT WT(r,θ,f)为某假定距离下垂直复声强实部warping 变换后的归一化频谱。确定l= 1时的归一化频谱绝对值最大值对应相干项的特征频率µ，以其为中心频率，确定带宽fd后，定义fH=µ+fd/2，fL=µ-fd/2。当代价函数最大时对应的距离即为估计距离。

当声源相对径向速度未知时，则可使用单矢量传感器估测声源相对速度的方法[22]对其进行估计。声压场与其波数谱G(k)构成了Hankel变换对，对声压在距离域进行Hankel变换后得到声压波数谱，即

对于信号中频率为f的单频部分，其第m阶简正模声压与水平振速存在如下关系：

其中，常系数σ为定值，k0=2πf/c。当声源以假定相对速度υ假定匀速运动时，对其进行Hankel 变换，此时波数域各阶简正模峰值对应波数设为假定水平波数krm假定，选取其中任一阶简正模的声压pm与水平波数vrm的峰值幅值，根据式(16)计算得到该阶简正模的理论水平波数krm。当信号相位不存在突变的情况下，理论水平波数与真实相对速度的乘积和假定水平波数与假定相对速度的乘积相等。通过该关系即可得到声源的相对径向速度，表达式为

2.3 声源深度估计方法

获得声源距离后，利用简正模非相干项与相干项模基匹配的方法进行声源深度估计。简正模自相关函数表达式为

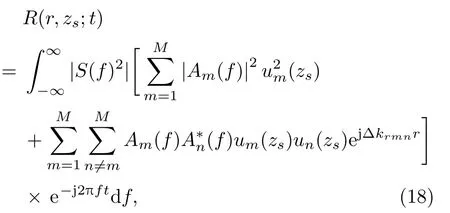
式(18)中，

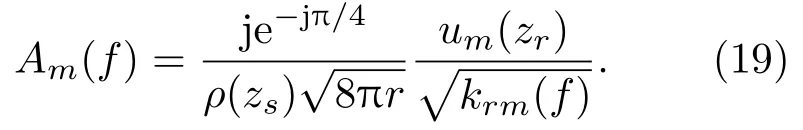
积分项的第一项表示所有同阶简正模的自相干，也称非相干项；第二项表示不同阶简正模之间的干涉，为相干项。自相关函数是关于时间对称的函数，在t= 0 时达最大值，且有R(r,zs;-t)=R(r,zs;t)。方法仅考虑时间t≥0的单边函数，简正模自相干项的相位为零，无时延，其集中于时域自相关函数零时延位置附近，脉宽为T= 1/B，B为信号带宽。分别提取Ri(r,zs;0 ≤t≤T)和Rc(r,zs;t > T)的频域表达式：

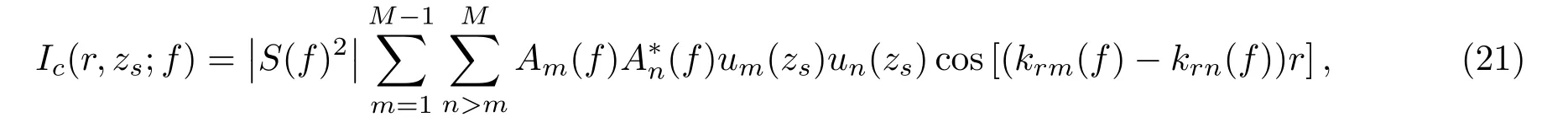
其中，Ic(r,zs;f)和Ii(r,zs;f)的除法运算可用来消除声源激发频谱S(f)的影响，定义

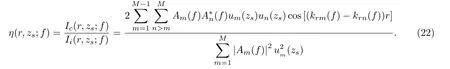
在声源距离已知的条件下，η(r,zs;f)是一个与声源深度、频率以及波导参数有关的复杂函数，即η(zs,f)。在海深范围内，利用理论模型计算得到的拷贝向量ηC(z)=[ηC(z,f1)ηC(z,f2)···ηC(z,fL)]，L为频段内采样点数。将实测数据向量ηR(zs)=[ηR(zs,f1)ηR(zs,f2)··· ηR(zs,fL)]与拷贝向量进行相关运算，即

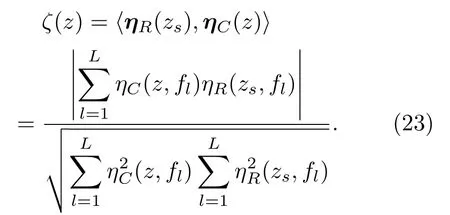
取最大相关系数对应的深度值，即为声源深度的估计值

文献[11]已对该方法的有效性及实用性给出推导与证明，在声场中存在三阶以上简正模时，声源深度估计结果唯一，不存在多值。该方法还可结合矢量声场中的质点振速及组合物理量完成测深。同时，距离估计方法与深度估计方法是独立进行的，深度估计是以距离已知为前提，但可以选择其他合适的频段进行深度估计以保证其估计性能。

3 仿真验证分析

仿真条件：等声速水文，声速1500 m/s，海深为100 m；单层海底，海底纵波声速为1700 m/s，密度为1.7 g/cm3，吸收系数为0.1 dB/λ，接收器深度99 m，声源距离为5～30 km，仿真中声源类型为宽带脉冲声源，以相对单矢量传感器10 m/s 的速度匀速运动。假设声源在单矢量水听器的58◦～63◦方位运动，声源运动方向的反向延接线与x轴夹角为60◦。

3.1 声源方位估计

图1为利用平均声强器法的声源方位估计结果图及相对径向速度变化图，估计结果准确。运动过程中可近似认为声源径向速度不变。

图1 平均声强器法声源方位估计结果及径向速度变化图Fig.1 Result of azimuth estimation by acoustic intensity average and diagram of radial velocity

3.2 声源相对速度及距离估计

对单矢量传感器相对径向速度估计方法进行验证。由于径向速度近似不变，此处按声源沿60◦方向匀速运动处理。选择声源频率为50 Hz、声源深度为30 m 的单频点信号进行处理。在工作频段内可选择任意频率的单频点信号，频率对方法性能无影响。在频率较低时，多普勒频移导致的影响较小，在此忽略其影响。选择声源距离为5～10 km的信号进行处理。假设声源相对径向速度为5 m/s，对声压及水平振速进行Hankel 变换，图2为声压及水平振速的波数谱。

图2 频率为50 Hz 的单频点信号声压、水平振速波数谱Fig.2 Wavenumber spectrum of source pressure and horizontal velocity at frequency of 50 Hz

由图2可知，此时声场中有三阶简正模起主要贡献，无需辨别其阶数。表1为三阶简正模各类数据统计。

通过式(17)计算得到相对速度估计值分别为9.92 m/s、9.87 m/s、9.94 m/s，相对误差分别为0.8%、1.3%、0.6%，证明该方法可行。对宽带信号加入高斯白噪声，分析测速方法在不同信噪比条件下的性能，图3为不同的信噪比条件下，测速结果的相对误差情况(图中纵轴截取至30%)。当信噪比大于0 dB时，估计结果相对误差小于10.61%。

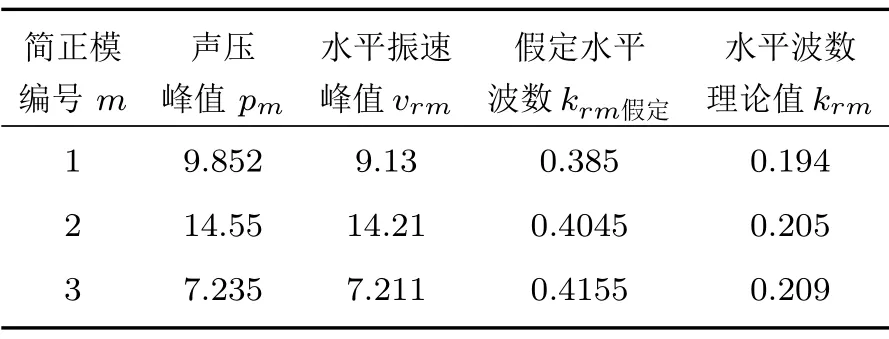
表1 波数谱中三阶简正模各物理量的数据统计Table 1 Data statistics of each physical quantity of third order normal modes in wavenumber spectrum

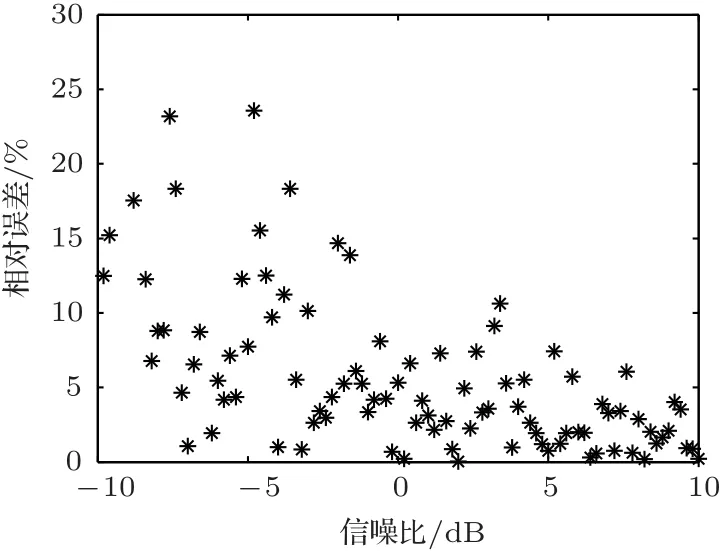
图3 测速估计相对误差随信噪比的变化情况Fig.3 The relative error of velocity estimation versus signal-to-noise ratio

得知声源运动速度后对声源距离进行无源估计。声源深度仍为30 m，声源距离为15～25 km，初始距离为15 km，选取信号时，两个信号之间间隔20 s 即距离间隔200 m，其他仿真条件同上。图4为假定初始距离15 km(即真实距离)和35 km 时垂直复声强实部warping 变换后的归一化频谱，声场中仅有前三阶简正模。

由图4可知，垂直复声强的FT WT(r,θ,f)图中不存在非相干项。在水平不变的波导中，当假定距离与真实距离不同时，FT WT(r,θ,f)图表现出两种不同的特征：其一，各相干项的特征频率并非真实特征频率；其二，相干项特征频率随距离的变化有所倾斜，即某相干项在不同距离上的特征频率不相同。以上两点皆可成为估计声源距离的重要依据，但上文已提到，若利用第一点特征进行测距则需要拷贝声场并预知声源深度。本文选用第二种特征，在不同的假定初始距离下，利用该段信号初始位置的FT WT(r,θ,f)能量最大值确定假定特征频率的中心频率，选择较窄的带宽，最终根据代价函数最大值估计实际初始距离。工作频率应选择较低的频率，当声源频率较大时，声场中的简正模阶数较多，不同阶简正模的声压与垂直振速之间的相干项特征频率差异可能会很小，容易出现混叠，不利于代价函数的使用。且随着距离的增加，高阶简正模衰减较大，归一化能量峰值位置可能会发生改变，如图5所示。为避免该情况的发生，本节仿真声场中仅存在三阶简正模。

图4 假定不同的初始距离，仅有前三阶简正模时的FT WT(r,θ,f)图Fig.4 Diagram of FT WT(r,θ,f)with first three order normal modes at different initial range

图5 简正模阶数较多时的FT WT(r,f)图Fig.5 Diagram of FT WT(r,f)with more order normal modes

图6为代价函数分布，搜索范围10～30 km，带宽选择0.2 Hz。红线表示代价函数最大值对应的估计距离，初始距离估计值为15.2 km，相对误差1.3 %，继而根据相对速度可以确定其他位置的声源距离。代价函数有一定的主瓣宽度，可能带来估计误差，但在可接受的误差范围内。

不改变仿真条件，在原信号中加入高斯白噪声，分析不同信噪比条件下测距方法的相对误差。图7为不同的信噪比条件下，测距结果的相对误差情况(图中纵轴截取至30%)。当信噪比大于10 dB时，估计结果相对误差小于11.33%，在未进行任何信号时间累积预处理时，该测距方法的实现需要较高的信噪比。

图6 信号初始距离为15 km 的代价函数Fig.6 Cost-function at the initial range of 15 km

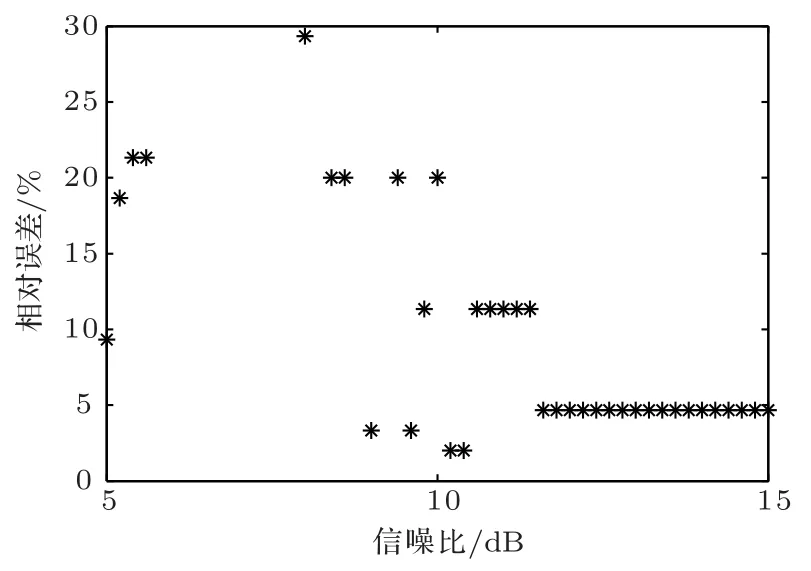
图7 测距估计相对误差随信噪比的变化情况Fig.7 The relative error of range estimation versus signal-to-noise ratio

3.3 声源深度估计

仿真条件同上，声源距离为5 km，声源深度范围为1～99 m。图8为声场中起主要贡献的分别为二阶、三阶以及频段内全部阶数，仅使用声压信息进行深度估计，不同声源深度的深度估计结果。

图8 利用不同简正模阶数时的声源深度估计结果Fig.8 Results of depth estimation at different orders of normal modes

图8中蓝色星点代表每一个深度的估计深度值。图8(a)中，仅利用第1 和第2 阶简正模时，在深度57 m 处分成两个深度区间，在各区间内存在多值性；图8(b)、8(c)中，当声场中起主要贡献的简正模阶数增多且大于等于三阶时，声源深度估计的多值性消除，且声源深度估计的敏感度增强。近水面声源深度估计的敏感度较弱，这是由于该深度范围(20 m 以内)简正模相干项与非相干项随深度变化缓慢。当声场中简正模阶数为三阶及以上时，方法可行，近水面声源深度敏感性问题可通过增加处理的简正模阶数改进。

而在矢量声场中，则有更多的物理量可以选择，使用质点振速的自相关函数以及声压-质点振速的互相关函数进行类似处理同样可以估计声源深度。图9为使用矢量声场中其他物理量或组合物理量的测深结果(全阶)。

图9 矢量声场中其他物理量或组合物理量的测深结果Fig.9 Results of depth estimation with other physical quantities or combined physical quantities in the vector field

4 结论

利用单矢量传感器作为接收器，除可以接收到声压信息外，还可同步接收到声场中的质点振速等矢量信息，相比于接收阵列，单矢量传感器在布放环节更具有优势，且通过声压与质点振速的组合处理可获得接收指向性，从而抑制干扰，同时提高信噪比，具有较好的实用意义。

利用水平方向两个正交分量的振速间关系可以对声源方位进行估计，从而仅依靠单矢量传感器即可完成对声源的三维定位。声场中仅存单一声源时，利用平均声强器方法估计声源方位，多声源时可考虑加权直方图等其他方法。水平不变的波导中，在自相关函数相干项特征频率不变性的匹配测距方法基础上，结合矢量声场理论及单矢量传感器声源相对速度测量方法，得到一种利用垂直复声强实部信息的无源测距方法。相比于之前测距方法，该方法无需预知声源深度信息也不再需要拷贝声场，减少了数据计算量，同时避免了原方法中需去除非相干项而可能带来的人为误差。完成距离估计后，利用自相关函数中非相干项与相干项的频域模基，对声源深度进行匹配估计。在声场存在三阶以上简正模时，深度估计结果具有唯一性。测深方法还可以利用声压与质点振速的组合量进行处理，获得同样的测量性能。

在一般的水平不变浅海波导条件下对三维定位方法进行仿真验证。结果表明利用不同阶的简正模皆可准确估计声源相对速度，平均相对误差为0.9 %，当信噪比大于0 dB 时，相对误差小于10.61%。已知声源相对径向速度后完成无源准确估计声源距离，当信噪比大于10 dB 时，距离估计相对误差小于11.33%。当声场中存在三阶以上简正模时，利用声压、质点振速及组合物理量皆可较为准确地估计声源深度，当简正模阶数较少时，近水面附近声源的深度估计结果敏感性较差，但敏感性随简正模阶数增加而获得改善。通过时间累积预处理可降低对信噪比的要求，是后续工作中需重点研究的内容。