单极随钻声波测井换能器感知信号类型的研究∗

张 超 陈 辉 胡恒山 王 军

0 引言

与电缆测井不同，随钻声波测井(Acoustic logging while drilling, Acoustic LWD)技术允许钻井和测井同时进行，在泥浆浸入前即可对地层完成测量，不仅缩短测井时间，还能够指导钻井方向。但随钻声波测井会记录到很强的钻铤波信号，往往掩盖后至的地层波，使地层信息不易被识别[1]。因此对钻铤波的研究一直是随钻声波测井的关注重点。

许多学者对随钻声波测井信号进行了理论模拟研究。Leggett 等[1]提出通过优化随钻声测井仪结构来抑制干扰信号。Wang 等[2]利用时域有限差分法计算全波声场，发现四极源更有利于地层横波测量。崔志文[3]用实轴积分(Real axis integration, RAI)法计算了不同地层中各模式波的频散曲线和全波波形。Zheng等[4]利用有限元法(Finite element method, FEM)研究了钻铤偏心情况下导波的声频散特性。Sinha 等[5]计算了随钻声波测井的径向位移信号和声压信号的幅度。Su 等[6]提出通过设置隔声器来阻止钻铤波的传播的方法，并利用频谱的禁带效应来减小钻铤波的影响。Wang等[7]指出，如果采用具有高纵横波速度和高密度的先进复合材料制成的钻铤，更有利于地层纵横波速度的测量。郑晓波[8]计算了单极和偶极随钻声波测井的分波传播特性。Yang 等[9]利用时域有限差分法分析了钻铤波的传播特性和能量辐射特性。Ji等[10]指出随着频率的增加，钻铤波的压强峰值逐渐从钻铤的内壁向外壁移动。迄今关于实验模型井的测量研究较少，Zhu等[11]利用小尺度声波测井仪器对各向同性和各向异性井眼模型进行了声波随钻测井实验。王军等[12]针对随钻声波测井中钻铤波干扰地层声波测量的问题，在实验室内开展了多极源随钻声波测井实验研究。

值得注意的是，上述研究中的模拟信号与实验信号存在较大差异(实验中的钻铤波明显更强[13])，但目前未见相关文献对该现象进行详细讨论。本文以压电方程和流-固边界条件作为切入点，针对边界处压强和位移连续的条件，对上述问题进行了理论模拟研究，即探讨单极随钻声波测井中换能器感知的信号是声压信号还是位移信号。本文将发射器、接收器、钻铤和井孔结构作为一个研究整体，计算了电压源激励下接收器记录的声压信号和位移信号，进而比较了它们的波形差异性。为了进一步验证有限元结果，随后将模拟波形与实验测量信号进行对比，结果表明径向位移波形比声压波形更接近实验测量信号。

1 随钻声波测井声-电响应的有限元模拟

1.1 随钻声波测井模型

将发射器、接收器、钻铤和井孔结构视为一个研究整体，模拟单极随钻声波测井环境下当电压脉冲激励发射换能器时接收换能器产生位移、声压信号和获得的电压信号。利用压电陶瓷的逆压电效应，钻铤上的发射器先将激励电压信号转化为声信号，携带地层信息的声波沿井孔结构传播到接收器后，接收器再利用压电陶瓷的压电效应将声信号转化为电压信号。与以往在假设声源振动模式情况下计算接收点处的声场不同，这里综合考虑压电效应与井孔传播效应，以便明确所测量到的电信号与同一位置上的力学量之间的关系。

设井、钻铤和换能器的对称轴重合，整个结构呈轴对称性。图1是任一给定环向角度时的剖面图，由内到外分为4 层，分别为流体层、钻铤层、流体层和地层。随钻声波测井仪由1 个环状的发射换能器和6 个环状的接收换能器组成，最小源距为3 m，相邻接收换能器间距为0.2 m，发射换能器和接收换能器结构相同。径向极化的压电换能器嵌入钻铤外壁，由内到外分为3 层，即背衬(环氧树脂)、径向极化压电陶瓷(PZT-5H)和金属外壳(铝)。其中背衬的作用是吸收压电振子的残余振动，减少残余振动的持续时间[14]。激励电压施加在压电陶瓷环的内外电极面上，产生的径向电场，进而由于压电效应引起压电陶瓷环的径向机械振动，同时激发金属壳体相同频率的径向振动，从而实现换能器的径向声辐射[15]。模型的其他参数如表1所示。模型中各构件的网格尺寸为(v/6f0)m, 其中v为各组件材料中波速的最小值，f0为激励电压的中心频率，计算时间步长为1×10−6s。

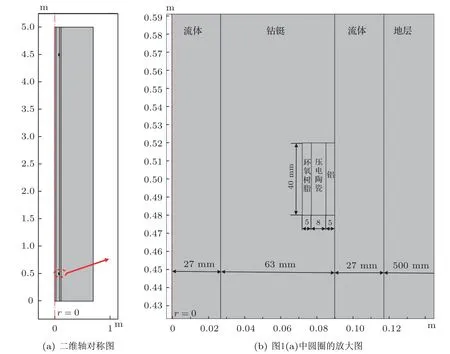
图1 随钻声波测井模型Fig.1 Acoustic LWD model

图2显示了换能器的前三阶振型及其对应的共振频率。换能器的一阶振型为压电圆管整体做扩张或收缩运动，无位移节圆；而二阶和三阶振型存在位移节圆，压电圆管不再整体做扩张和收缩运动，而是分段做扩张和收缩运动。可见一阶振型能更好地模拟测井中的单极声源。将激励电压的激励频率控制在换能器一阶共振频率之下，取为4～16 kHz。激励电压的表达式为

其中，T0=2.5×10−4s，f0是激励电压的中心频率，f0= 10 kHz。图3为激励电压的时域波形和频域波形。

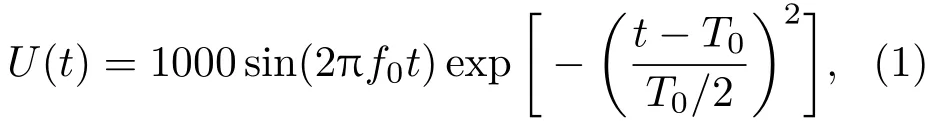
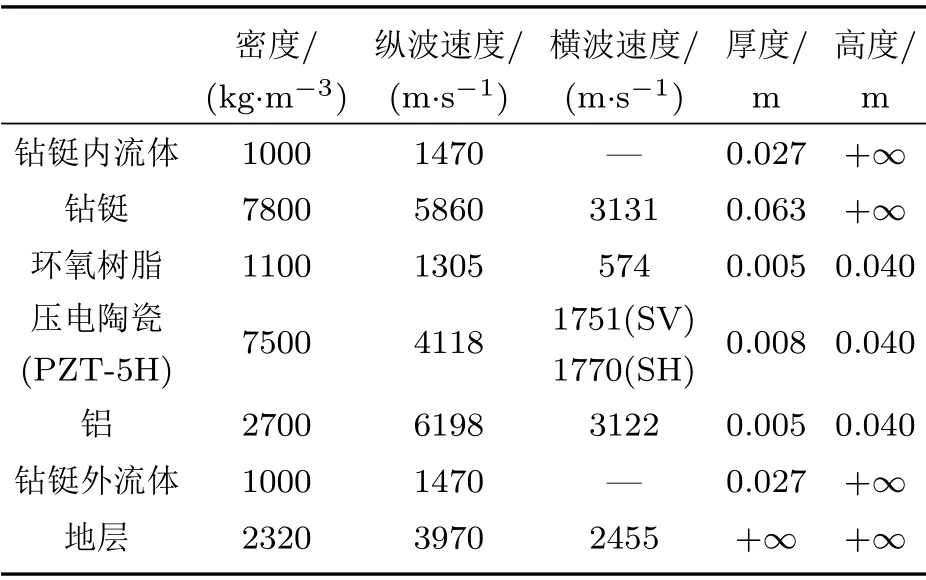
表1 流体、钻铤、压电换能器及地层的材料及几何参数Table 1 Material and geometric parameters of fluid, drill collar, piezoelectric transducer and formation

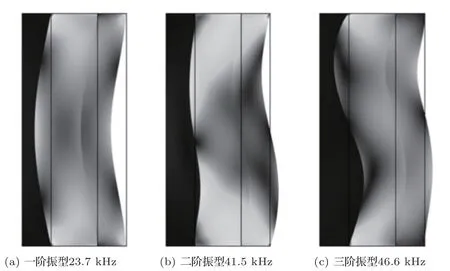
图2 换能器的振型及其对应的频率Fig.2 The vibration shape of the transducer and its corresponding frequency

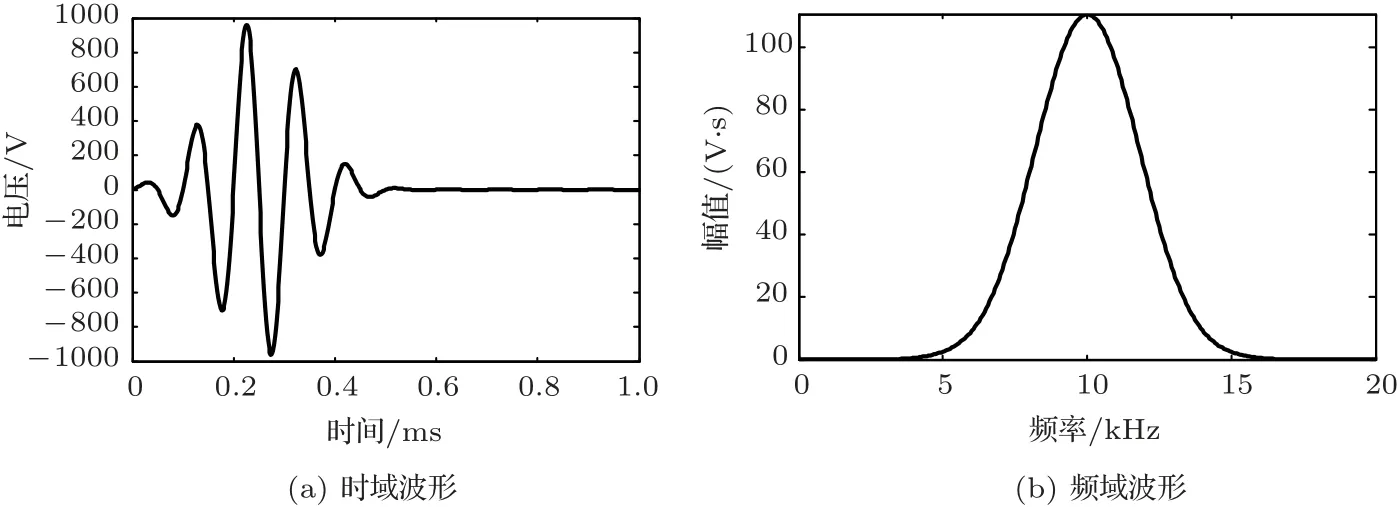
图3 激励电压的时域和频域波形Fig.3 Time domain and frequency domain waveforms of excitation voltage

1.2 模拟结果

利用有限元软件中的域点探针，可拾取接收换能器外壁中心处的电压波形、径向应力波形(即为换能器周围流体中的声压波形)以及位移波形。图4为模型的钻铤外壁处的距声源最近的接收器接收到的声压和径向位移信号以及由压电陶瓷的压电效应激发的电压信号，3 种信号均含有钻铤波、横波和斯通利波，且相应模式波的到时一致，钻铤波与横波的相位相差很小。对比可以看出3 种信号最显著的差别为：电压信号与径向位移信号的钻铤波幅度均强于斯通利波，二者波形相近；而声压信号的钻铤波幅度弱于斯通利波，与电压信号差距较大。因此认为径向位移信号可以更好地反映换能器接收到的电压信号，即单极随钻声波测井换能器主要感知的信号类型为径向位移。

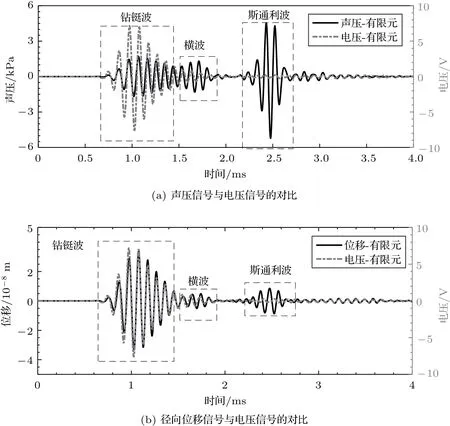
图4 有限元模型中声信号与电信号的对比Fig.4 Comparison of acoustic and electrical signals at the receiving transducer in FEM model

为了验证有限元计算的精度，如图5所示，分别对比了声压信号和位移信号的有限元方法与实轴积分方法的计算波形，两种信号均含有钻铤波、横波和斯通利波。两种方法模拟的声信号波形中各波群的到时、相位以及幅值均一致，可见有限元方法的模拟是有效且精确的。值得说明的是，为了更好地比较两种方法，在有限元模拟中未加入压电模块，只考虑波的传播过程，即以声压源作为激励，接收声压信号和位移信号。

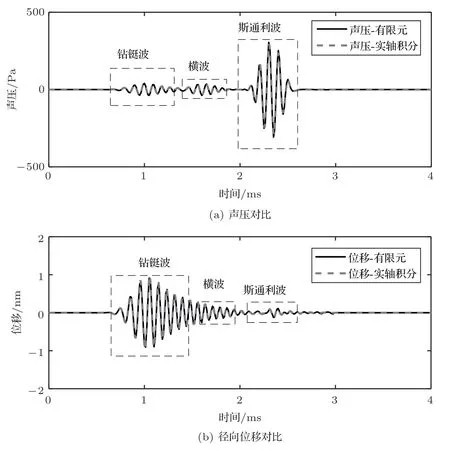
图5 有限元方法与实轴积分法的对比Fig.5 Comparison of FEM model and RAI method

图6为井孔内声压信号和位移信号中钻铤波幅度随径向位置的变化，图中3 个竖线从左到右分别为钻铤内壁、钻铤外壁和井壁。可见声压信号中钻铤波能量主要集中在钻铤内壁，而径向位移信号中钻铤波能量主要集中在钻铤外壁。因此在光滑钻铤上通过刻槽方式进行隔声时，采用外刻槽可望获得到更好的效果，这与以往学者[8]建议的内刻槽方式是不同的。关于内刻槽和外刻槽后随钻声波测井的响应，杨玉峰[16]做了细致的研究，本文侧重讨论检测信号的力学类型。

2 实验对比

随后将实单极随钻声波测井实验接收的电压信号[12](图7(a))与实轴积分获得的声压信号、位移信号对比。如图7所示，3种信号含有相同的波群，即钻铤波和斯通利波，且相应模式波的到时一致；实验信号与径向位移信号中钻铤波幅度最大，信号比较相近；而声压信号中斯通利波幅度最大。这与第1节中有限元模型得到的结果相同。可见利用径向位移信号可以更好地反映出实验信号的趋势，也就是说单极随钻声波测井换能器主要感知的信号类型为径向位移。

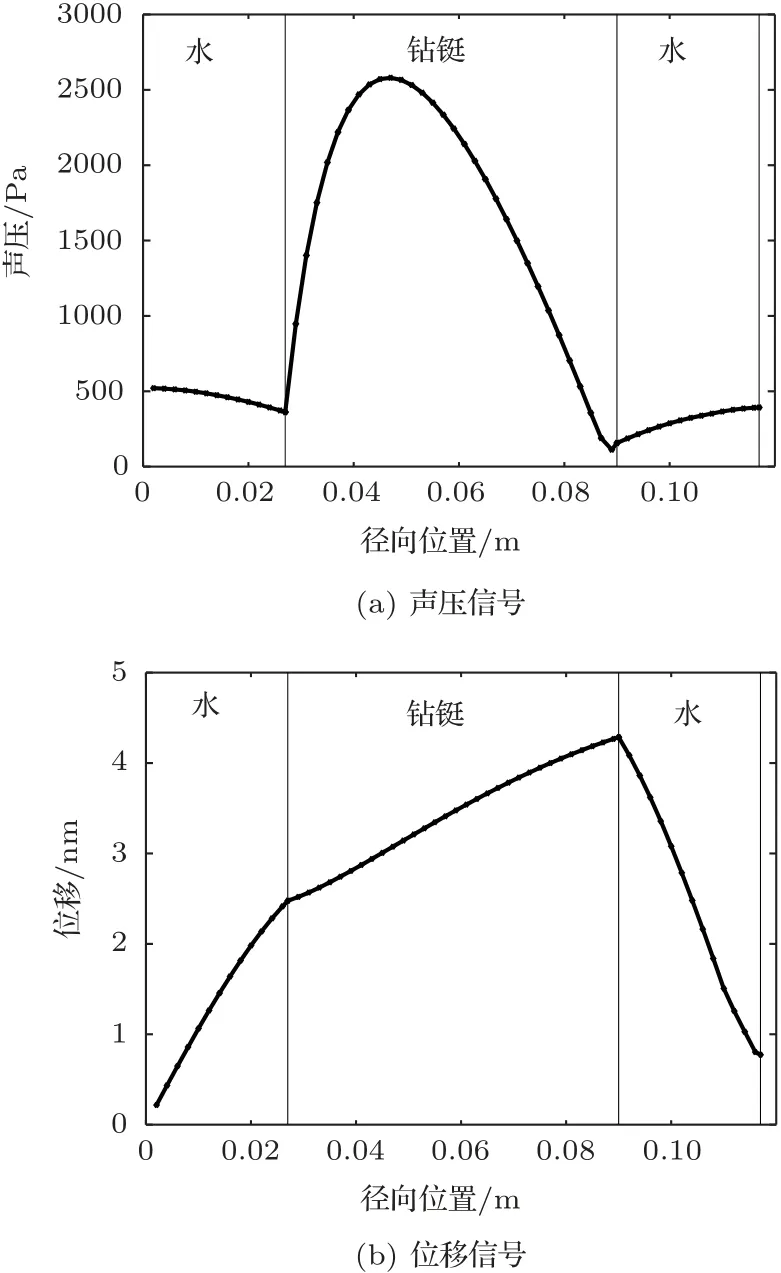
图6 钻铤波幅度随径向位置的变化Fig.6 The amplitude of the drill collar wave varies with the radial position

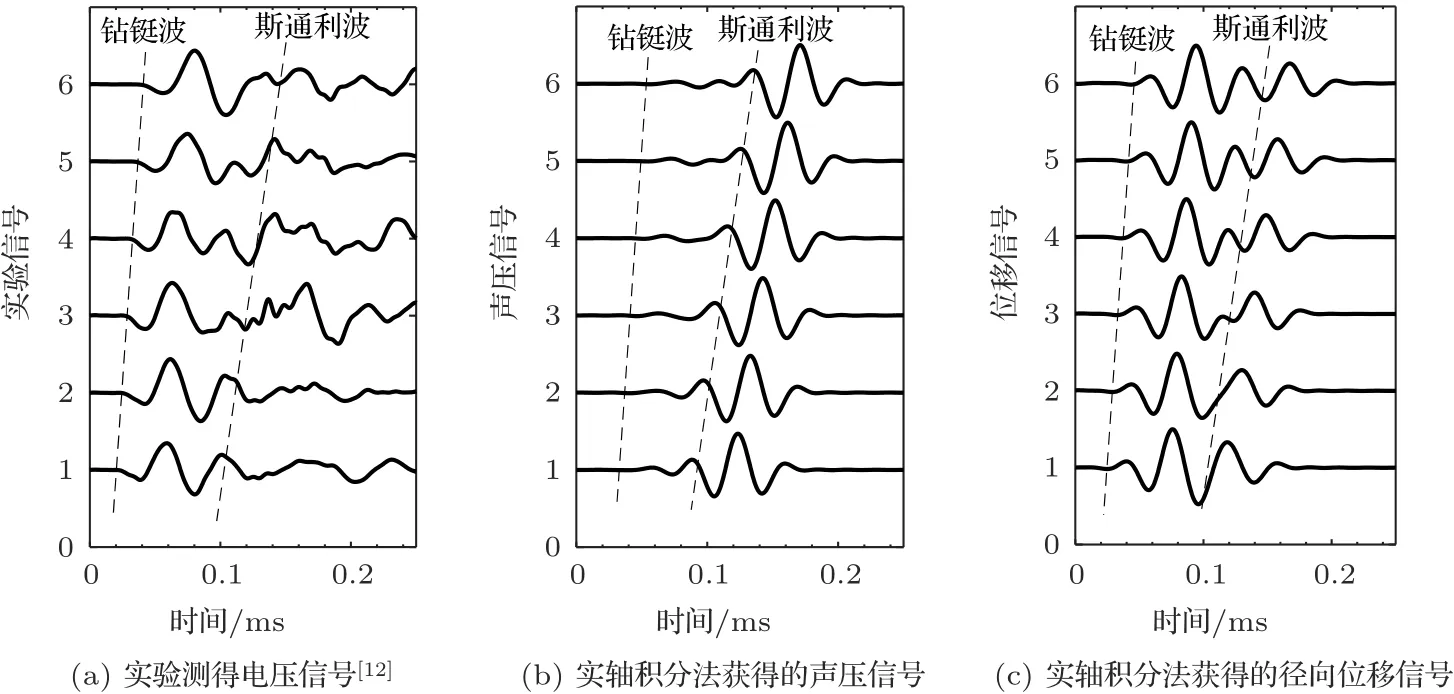
图7 实验信号与解析信号的对比Fig.7 Comparison of experimental signal and analytical signal

3 结论

本文将换能器-钻铤-井孔-地层视为一个整体，考虑压电和井孔传播效应，计算获得了电压脉冲激励发射换能器时的随钻声波测井响应。计算获得的径向位移信号比声压信号更贴近电压波形，也与实验采集的电压信号更相符。可见，在单极随钻声波测井中，换能器主要感知的是径向位移信号。研究还表明，径向位移信号中钻铤波的能量主要集中在钻铤外壁，声压信号中钻铤波的能量主要集中在钻铤内壁。这些结论是针对光滑钻铤和井孔内充满理想流体的情况下得出的。