拖曳阵被动合成孔径目标深度稳健估计∗

李天宇 李 宇 黄海宁 迟 骋

0 引言

目标深度估计在水下目标探测识别领域发挥着越来越重要的作用，同时也面临着信息获取难度大和环境影响复杂等多方面的困难。学者们经过几十年的研究，总结了匹配场处理(Matched-field processing, MFP)方法和匹配模处理(Matched-mode processing, MMP)方法是两种可行的方法[1−2]。与MFP 相比，MMP 具有物理意义明确、计算量小和鲁棒性好的优点，因此得到了更广泛的应用[3−4]。因为利用垂直阵(Vertical line array, VLA)可以方便地计算模态深度函数，所以早期的探测设备以VLA 为主。Bogart 等[5]证明了如果水平阵(Horizontal line array, HLA)的孔径足够长，利用不同阶模态的水平波数差异也可以分离模态，并提出了有效孔径的概念。Premus 等[6]通过大孔径水平阵提取低阶模态的能量进行水面、水下声源的分辨。李鹏等[7]和郭良浩等[8]学者对水平阵模态域波束形成进行了更深入的研究。

与固定式VLA 和HLA 相比，水下无人平台(Unmanned underwater vehicle, UUV)搭载拖曳阵的探测方式具有灵活性高、隐蔽性好等优势。Chouhan 等[9]利用多重信号分类(Multiple signal classfication, MUSIC)方法从拖曳阵数据中估计模态波数。黄勇等[10]利用合成孔径方法进一步提高了波数分辨力，但由于不同阶简正波之间的相干性强，MUSIC方法在基阵运动距离大于模态相干距离时才能正确分离波数。Yang[11]利用声压和深度分离的格林函数之间的Hankel 变换关系，使用VLA接收数据进行声场积分，准确估计了运动声源波数谱。

和固定式探测设备相比，UUV 搭载的拖曳阵主要受到来自3 个方面的干扰。一是UUV 和感兴趣目标之间动态变化的位置关系容易导致模型失配。二是UUV 自噪声的干扰，由于UUV 自噪声和感兴趣的目标的辐射噪声频带相近甚至重合，因此消除自噪声的干扰具有重要意义。Candy 等[12]、Sullivan等[13]和Cederholm 等[14]许多学者研究了常规大型拖曳阵的载体自噪声抑制问题，但大多数研究没有指明如何选择参考信号或参考信号很难获取。Chi 等[15]在拖曳阵探测问题中研究了如何使用阵处理方法获得参考信号。三是阵列瞬时随机加速度扰动，由于UUV 容易受到海洋湍流和内波的影响，因此阵列存在明显的瞬时随机加速度扰动，在接收信号中引入了相位抖动。

针对上述存在的3 种干扰，本文提出了一种稳健的拖曳阵被动目标深度估计技术。首先在每个阵元上利用自适应滤波算法实现自适应噪声抵消(Adaptive noise cancellation, ANC)，并通过二阶锁相环(Phase locked loop, DLL)滤除相位抖动，经过两步抗干扰预处理得到了纯净的接收信号。然后对测量的声场空间分布进行距离积分，计算模态估计的波数谱，声场积分方法对阵列的运动形式没有严格要求。最后从中提取模态能量并利用模态匹配器在不同深度进行匹配，估计出目标深度。

1 浅海简正波模型

假设浅海环境为与距离无关的水平分层波导，目标声源在深度zs以速度vs匀速水平直线运动，UUV 在深度zr以速度vr匀速水平直线运动，声源和UUV 的速度矢量与两者位置连线的夹角分别为θs和θr，声源辐射频率为Ω。根据文献[16]，以基阵为参考系的接收信号表达式为

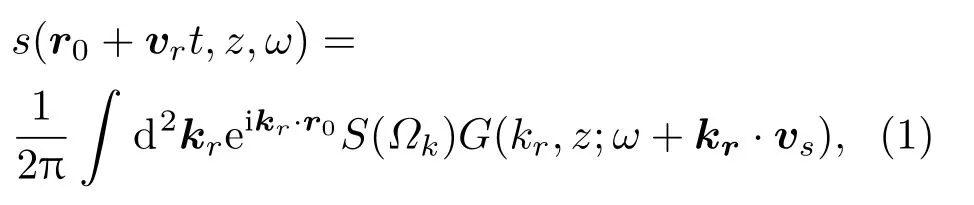
其中，kr是水平波数矢量，G(kr,z;ω+kr ·vs)是频率为ω+kr ·vs的深度分离的格林函数，S(Ωk)是声源功率谱，Ωk是包含多普勒频移的声源频率，Ωk=ω-kr ·(vs-vr)。实际探测时，声源到基阵的距离一般远大于探测基阵孔径，因此，为了简化计算，可以近似认为θs和θr保持不变。利用Hankel变换代替水平波数的二维Fourier变换，再将格林函数表示为具有离散水平波数的模态累加的形式，可以得到简正波模型下的接收信号表达式为

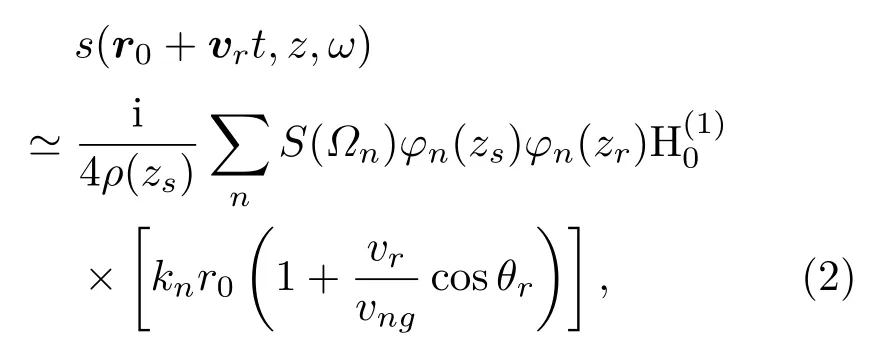
其中，Ωn=ω -kn(vscosθs -vrcosθr)=ω[1-(vs/vnp)cosθs+ (vr/vnp)cosθr]，vng和vnp分别是第n阶模态的群速度和相速度，kn是Sturm-Liouville 本征方程在确定边界条件下的解，表示离散的水平波数，φn(z)是对应的本征函数。

2 确定运动状态下的目标深度估计

本节针对运动状态确定的阵列提出基于被动合成孔径的目标深度估计算法，解决未知随机加速度扰动和自噪声干扰的预处理算法在第3 节提出。由于简正波不同模态的水平波数差异小，而且拖曳阵物理实孔径有限，因此需要利用UUV 的机动能力，对目标信号进行持续观测以获得足够的空间增益。已经有一些学者使用被动合成孔径方法以提升模态估计精度[11]。使用传统被动合成孔径方法能够形成虚拟阵元的大孔径，当拖曳阵非匀速直线运动时需要设计复杂的相位补偿算法，甚至可能失效。本节采用的声场积分方法也是一种合成孔径方法，但与前述方法不同的是，首先通过阵处理在每个测量位置独立计算声压，然后对其进行距离积分获得空间增益，最后进行模态匹配得到目标深度估计结果。由于不需要先合成虚拟孔径再进行参数估计，因此阵列可以以任意运动形式进行探测，保证了算法的稳健性。

2.1 声场积分法模态估计

首先假设已得到不存在自噪声和阵列瞬时随机加速度扰动的阵列接收信号，将基于浅海简正波模型的信号表达式(2)转换到时域。为后续表述方便，假设目标位于拖曳阵艉部端射方向，即θr= 180◦，拖曳阵阵元数为M，以d为阵元间隔均匀分布，拖曳阵远离目标一端的阵元为参考阵元，探测开始时，参考阵元和第m个阵元与声源的距离分别为r0和rm=r0-(m-1)d。根据第1 节的分析，当声源辐射频率为f0的单频信号时，UUV 接收到一串经过多普勒频移的离散频点信号，对应的各阶简正波频率为ωn= 2πf0+kn(vs-vr)，因此第m个阵元的时域信号为

为了恢复声场空间分布p(r,zr)，首先将阵元接收信号划分为长度相同的一系列数据块，数据块总数为Q，每个数据块持续时间为T，包含L个采样点，T=L∆t，其中∆t是信号采样间隔，用tq,l=qT+l∆t表示第q个数据块中第l个采样点对应的时间，阵列在数据块持续期间的位移量为R，可以将式(3)转换为

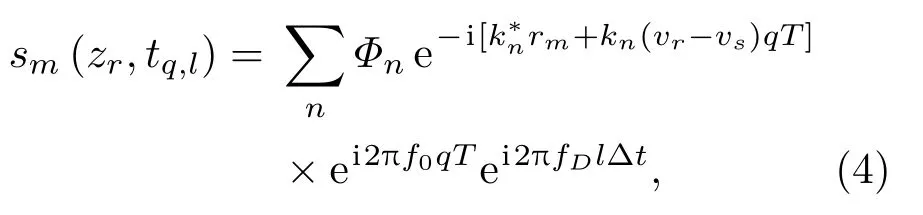
其中，fD=f0[1-(vr-vs)/c]是多普勒频移后的接收信号频率。对每一个数据块进行Fourier 变换可以得到

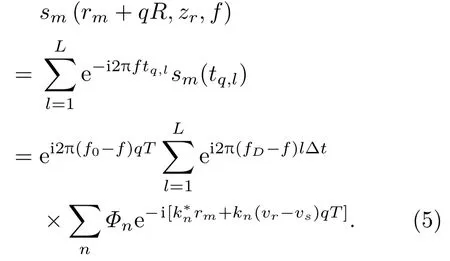
根据式(5)，声压的空间分布可以通过每一个数据块的在f=fD的Fourier 变换结果乘以e−i2π(f0−fD)qT得到估计，即

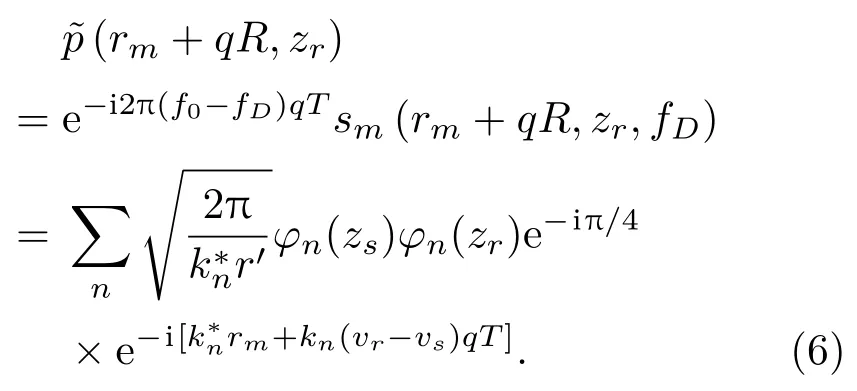
观察式(6)容易发现，动态声场中的声压分布与声源静止时情况有两点不同。首先，指数函数中的速度差表明，由于声源运动，阵列在第q个采样区间的测量声压的位置到声源的实际距离为(vr-vs)qT，而非阵列的空间位移qR。此外，指数函数中的k∗nrm表明，空间各处不同阶简正波之间的固有相位差受初始距离和阵列速度共同影响。

在与距离无关的水平分层环境中，窄带声源的声压p(r,zr)和深度分离的格林函数g(kr,zr)之间构成Hankel 变换关系，如果满足远场条件，则可以用Fourier变换进行近似，即

其中，S(r′)是用于补偿能量衰减的加权系数，比较式(6)与式(7)可以发现，可以在式(7)的离散形式基础上稍加修改得到深度分离格林函数的估计值，也就是模态波数谱，如下所示：

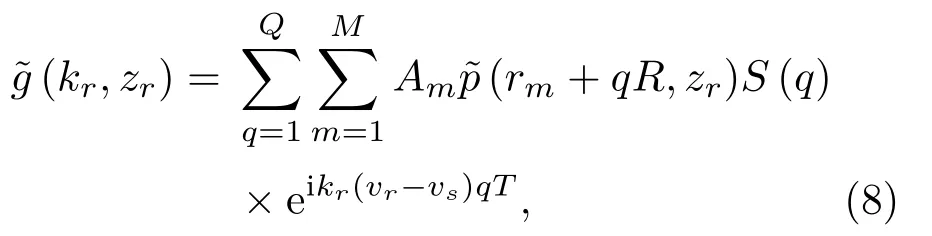
其中，S(q)是和S(r′)对应的离散形式的加权系数，可以根据每个数据块的信号能量的倒数计算得到。Am= eikrmd是模态域导向向量的第m个分量，通过计算阵元声压的加权和获得了模态域的阵增益。将式(6)代入式(8)不难发现，估计的模态波数谱(kr,zr)和模态深度函数之间的关系为

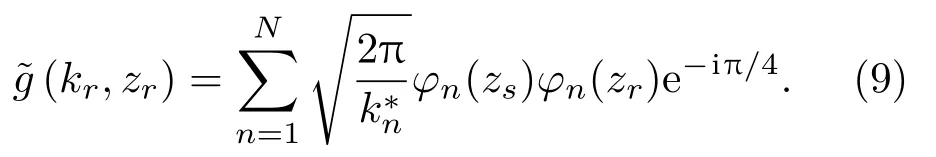
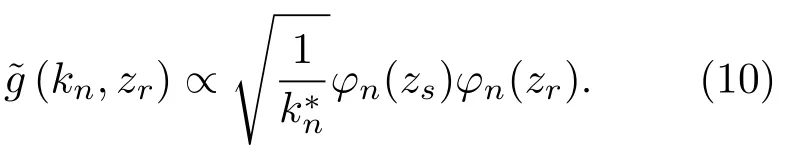
以上的分析假设阵列和目标都处于匀速直线运动状态，当阵列速度变化时，只需要针对每个数据块独立计算声压，然后根据UUV 记录的速度计算每个测量位置对应的和目标的相对距离，最后代入声场积分式中即可。在仿真中将做进一步分析。

2.2 模态匹配

在得到接收信号的波数谱后，可以采用模态匹配的方法估计目标深度，模态匹配器结构为Camberra 距离的负指数：

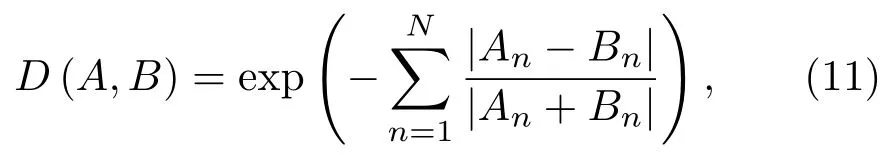
其中，A和B分别是估计的归一化模态能量和根据已知环境信息仿真的归一化模态能量，An和Bn分别是其第n阶模态对应的能量。在对环境信息进行测量以后可以使用Kraken 软件仿真各阶模态的水平波数和模态深度函数。结合仿真的波数信息可以从2.1 节计算的模态估计波数谱中提取模态能量，即在仿真波数附近搜索波数谱峰值。由于不同阶模态的能量一般差异较大，如果采用传统的欧式距离进行度量，不能反映模态能量变化和起伏带来的影响，因此采用式(11)定义的Camberra 距离的负指数来度量模态匹配度，Camberra 距离是经过尺度调整的差的绝对值之和，在分母中引入估计值和仿真值的和，可以将绝对能量偏差转化为考虑了模态能量起伏的相对偏差。通过计算其负指数可以将模态匹配度映射到[0,1]。将假想目标深度从海面到海底进行遍历，分别计算对应的模态匹配度，最大值对应深度就是估计的目标深度。

3 抗干扰预处理

第2节中推导的基础是阵元接收信号不包含航行器自噪声，同时也不受阵列瞬时随机加速度扰动影响。然而在实际探测过程中，始终存在这两部分干扰，因此需要对数据进行预处理。实验数据显示，拖曳阵接收的UUV自噪声以300 Hz 以下的低频线谱为主。这也符合噪声产生的机理，因为UUV的螺旋桨转速不足以产生空化，所以螺旋桨噪声以和轴频、叶频相关的线谱为主，同时UUV在水下航行，所以不存在壳体与水面相互作用带来的宽带噪声。设计自适应滤波器实现ANC，主要是考虑参考信号如何获取以及选择何种自适应算法。Chi 在文献[15]中提出了一种解决问题的思路。

选择滤波器长度的原则是保证其大于噪声自相关时间和从航行器到每个阵元的声传播时延。本文研究的拖曳阵采样率为10 kHz，从最远端阵元到UUV 的距离dmax为50 m，典型浅海环境深度h不大于100 m。由于自噪声频率较低，波长长度与阵列空间结构相差不大，因此从UUV 到拖曳阵的传播过程是一个复杂的近场问题，不适合用声线的反射建模。尽管如此，用海面/海底反射路径的时延作为信号时延的一个大致估计是合理的。假设声速c=1500 m/s，从载体出发经一次海面/海底反射到最末端阵元的最大传播时延τmax的计算公式为

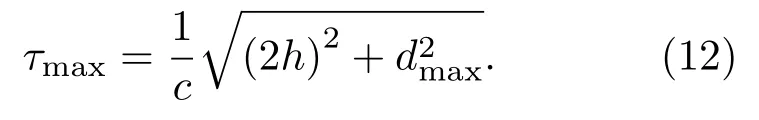
根据上述几何结构计算，τmax<0.13 s。计算测量信号的自相关函数如图1所示，容易发现当自相关时间大于0.2 s 时，信号相关性迅速减弱。综合考虑传播时延和自相关时间，滤波器长度应大于2000。

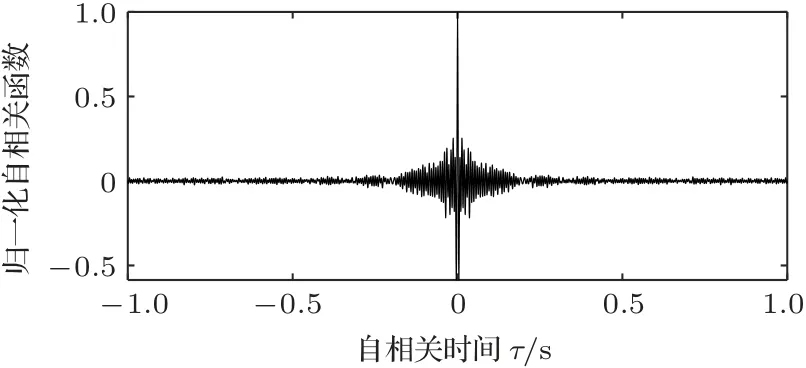
图1 自噪声自相关函数Fig.1 Autocorrelation function of the self-noise

在ANC 应用中，通常在噪声源附近放置传感器采集参考信号，然而在水下应用中，额外放置水听器的方案会显著增加设备复杂性，因此考虑利用波束形成方法直接从阵列接收信号中获取参考信号。实验过程表明，拖曳阵在工作状态下近似平直且与UUV 在同一深度，因此可选择阵列指向UUV 的方向计算各阵元时延，对阵元采集信号进行升采样后反向时延叠加，再降采样得到自适应滤波器的参考信号。

不同的自适应算法具有不同的计算复杂度和收敛特性，选择算法的目的主要是在计算复杂度和收敛特性之间进行平衡。根据上述分析，在拖曳阵ANC 应用中阵元数较多，并且滤波器长度较长，因此应尽量减小计算复杂度以减轻处理器压力。本文选择频域分块最小均方(Frequency block adaptive least mean square, FBLMS)算法作为阵元数据预处理算法。FBLMS 算法借助快速Fourier变换(Fast Fourier transformation, FFT)实现快速卷积和快速相关运算，并且可以通过对频域抽头权向量使用独立的归一化步长参数，显著提高算法的收敛速度，有关FBLMS 算法的更多内容可以参考文献[17]，结合上文对滤波器长度的分析，本文的滤波器参数选取为滤波器长度2048，块长度2048。

2.1 节中提出的声场积分法可以在阵列非匀速运动，但确知运动形式时获得测量数据的模态估计，实际应用中，阵列接收信号还由于受到未知的瞬时随机加速度扰动而产生相位抖动，需要采用针对性预处理进行消除。二阶锁相环具有快速收敛的相位跟踪性能，在水下声通信中发挥着重要的作用[18−19]。在相位抖动抵消预处理中，首先对PLL的输出相位进行平滑，然后从输出相位中减去平滑后的相位可以得到相位抖动的估计，最后根据相位抖动估计对阵元数据进行补偿。抗干扰算法的流程图如图2所示。

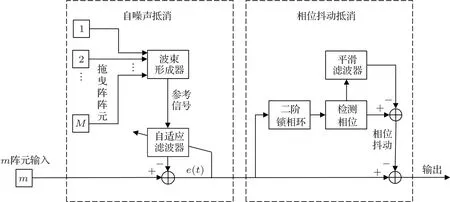
图2 抗干扰算法流程图Fig.2 The schematic of anti-interference algorithm

4 仿真实验

仿真分为3个部分，首先在UUV非匀速运动的情况下将本文提出的方法与SA-SAMV方法进行比较，然后在受UUV 自噪声干扰的情况下研究抗干扰算法带来的稳健性提升，最后仿真目标频率变化和合成孔径距离的变化对目标深度估计的影响。

描述声源和UUV 拖曳阵的运动状态以及声学环境参数的浅海波导模型如图3所示，水深44 m。声源频率为145 Hz，深度为zs=23 m，向左水平速度为vs。拖曳阵阵元数为16，相邻阵元间距为1 m，深度为zr= 11 m，向右水平速度为vr。声源处于拖曳阵艉部端射方向，两者背向运动，初始距离为2000 m。

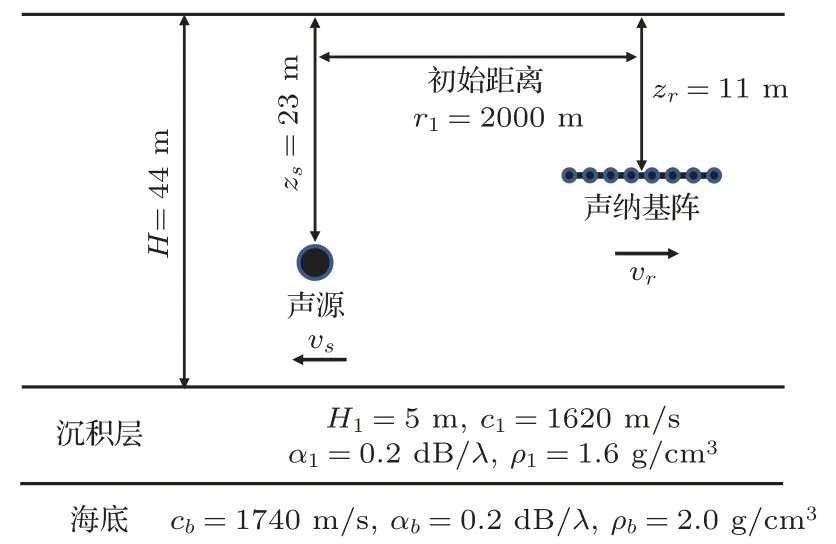
图3 浅海波导模型Fig.3 The model of shallow sea waveguide

4.1 UUV非匀速运动仿真

选择SA-SAMV 方法作为对比方法，它的原理是首先通过合成孔径算法将运动小孔径水平基阵扩展成虚拟的大孔径水平基阵，然后利用稀疏近似最小方差准则估计简正波模态能量，优势是可以在较小的合成孔径基础上得到高分辨率模态估计，缺点是当阵列非匀速运动时表现不佳。在图3所示的浅海环境中，假设声源保持vs= 0.5 m/s 的速度匀速运动。拖曳阵先做匀加速运动再做匀减速运动，初速度vr= 2 m/s，匀加速阶段的加速度为ar= 0.005 m/s2，持续200 s，匀减速阶段的加速度为ar=-0.005 m/s2，持续200 s，探测时间总计400 s。根据运动关系，相对声源的位移为1200 m。仿真阵列采样率10 kHz。声场积分法中的数据块长度为4096，独立处理每块数据块时以该时间段内的平均速度计算多普勒补偿相位。SA-SAMV 方法使用全部测量数据进行目标深度估计，因此合成孔径距离为1200 m。SA-SAMV方法和声场积分方法的模态估计结果和目标深度估计结果分别如图4和图5所示。从图4(a)中可以看出，在UUV 非匀速运动的情况下，SA-SAMV 方法的模态估计误差很大，基本无法从中提取模态能量信息。从图4(b)中可以看出，声场积分法的模态估计结果保持了较好的分辨率。从图5中可以看出SA-SAMV 方法的目标深度估计已经失效，而声场积分方法的目标深度估计具有较高的稳健性。

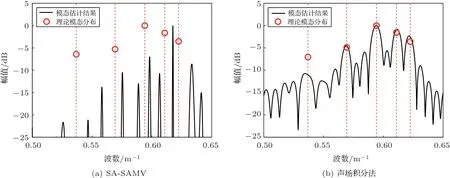
图4 拖曳阵非匀速运动时的模态估计Fig.4 Modal estimation at unsteady speed

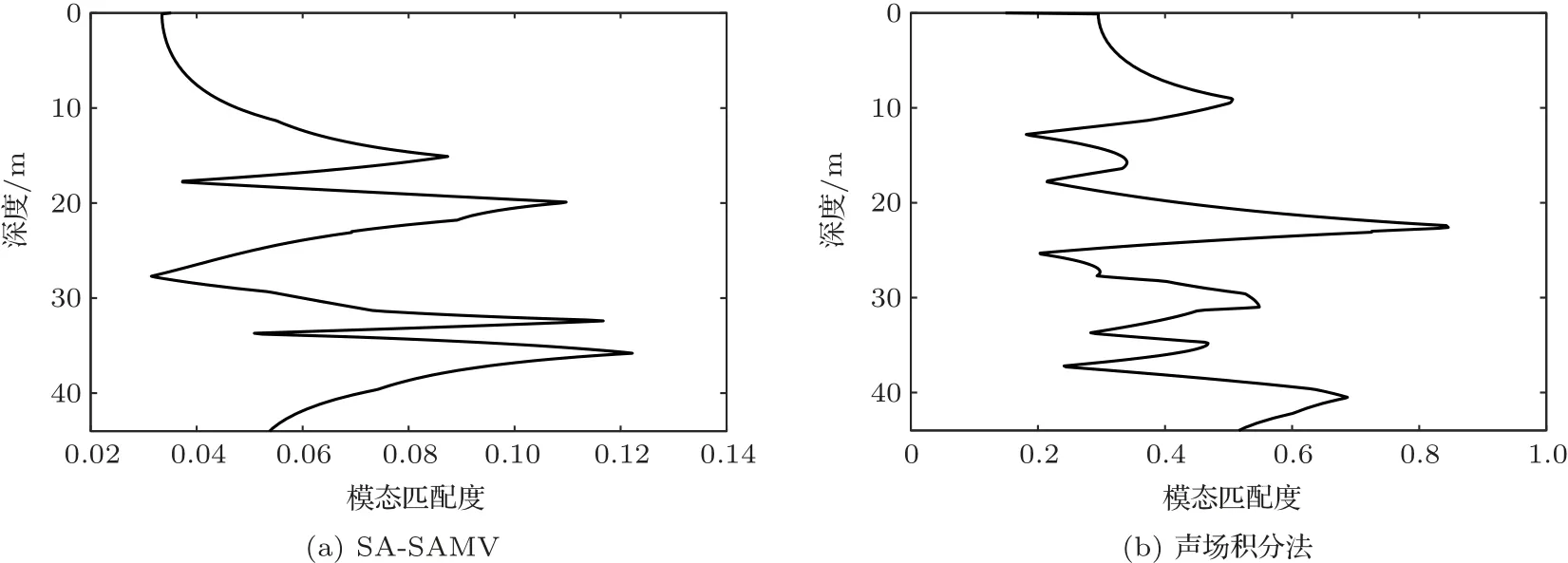
图5 拖曳阵非匀速运动时的目标深度估计Fig.5 Target depth estimation at unsteady speed

4.2 拖曳阵ANC仿真

本节对UUV 拖曳阵ANC 进行仿真，相位抖动滤波的预处理将在实验数据处理中进行研究。干扰信号是实验中首阵元测量的自噪声信号，并对其进行窄带滤波，通带频率设置为[140 Hz, 160 Hz]。将滤波后的窄带噪声叠加到4.1 节无自噪声干扰的仿真数据中，得到自噪声干扰下的仿真接收信号，单通道功率谱如图6所示。从图6中可以看出，UUV自噪声的中心频率为152.5 Hz，与仿真的目标线谱接近，由于UUV自噪声能量较强，因此在功率谱上，目标线谱已经不明显。将经过抗干扰预处理的模态估计结果和深度估计结果与未经抗干扰预处理的结果进行对比，如图7和图8所示。通过对比可以看出，抗干扰预处理改善了波数谱和目标深度估计结果，但与无干扰情况下的模态估计结果相比，丢失了最高阶模态。在实际应用中选择模态匹配的模态阶数时，通常只选择低阶模态，这是因为低阶模态在波导中的传播更加稳定，更加容易被识别；另外，高阶模态对应的深度函数有较多的波腹和波节，在模态匹配时引入高阶模态实际上降低了匹配算法的稳健性。图8中的深度估计是选择1～4 阶模态的结果。

图6 自噪声干扰下仿真信号功率谱Fig.6 The power spectrum of simulated signal under self-noise interference

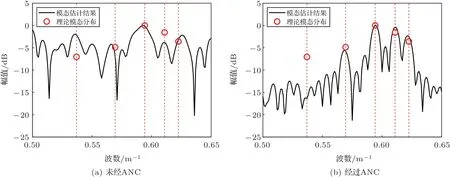
图7 模态估计波数谱Fig.7 The estimated wavenumber spectrum with and without ANC

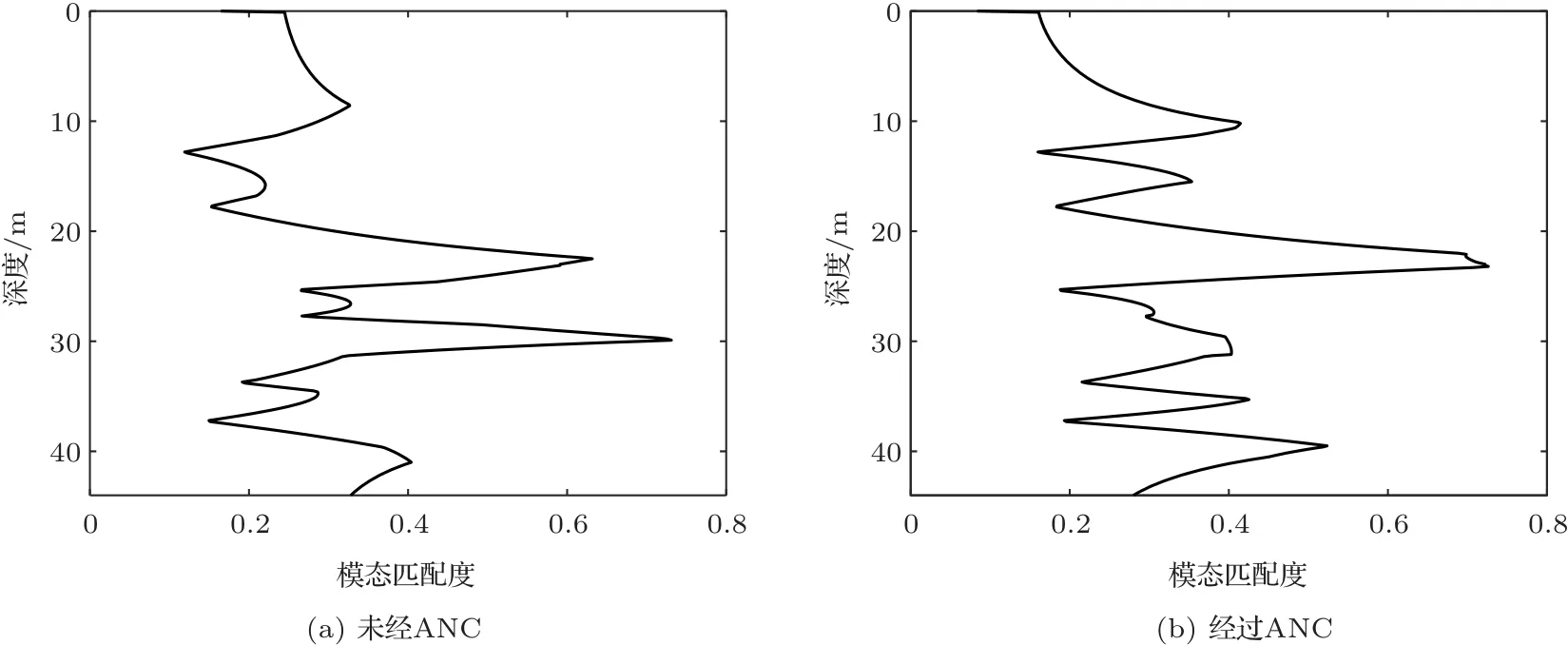
图8 深度估计Fig.8 The target depth estimation with and without ANC

4.3 深度估计误差的影响因素

为进一步研究目标深度估计误差的影响因素，假设准确测量了环境信息，在4.2 节中的自噪声干扰下使用声场积分方法进行目标深度估计。声源频率为145 Hz 和245 Hz，以自噪声作为干扰源定义的信干比变化范围为-20～20 dB，合成孔径距离为1000 m，通过100 次Monte Carlo 仿真得到经过ANC和未经ANC的目标深度估计误差如图9所示，从图9中可以看出，ANC 预处理可以显著降低自噪声干扰导致的目标深度估计误差，如果不经过ANC预处理，当信干比低于0 dB时，误差明显增大，导致目标深度估计失效。经过ANC 预处理可以在更低信干比实现目标深度估计。在信干比固定为10 dB的情况下，合成孔径距离变化范围为200～1000 m，频率为145 Hz、195 Hz和245 Hz，通过100次Monte Carlo 仿真得到的目标深度估计误差如图10所示。从图10中可以看出，声源频率一定时，目标深度估计误差随合成孔径的增加而减小，当合成孔径距离足够大时，目标深度估计误差不再进一步随合成孔径的增加而减小；当合成孔径和信干比一定时，目标深度估计误差与声源频率有关，对低频声源的模态估计更准确，这是因为低频声源激发的简正波阶数较少，波数间隔较大，易于分辨和估计。在实际应用中往往存在多目标，根据探测到的目标相对阵列的方向，可以对不同方向的目标并行地计算其声压的空间分布。由于式(8)利用波数域阵处理获得了阵增益，阵列的阵元数越多则阵增益越高，因此在计算某个方向的目标的模态估计波数谱时，来自非当前方向的其他目标的信号可以等效为波数域的噪声。对多目标情况进行仿真，假设除端射方向有感兴趣的水下目标外，在其他方向还有一个静止的干扰目标，深度为5 m。改变干扰目标的方向和频率，得到感兴趣目标深度估计误差随波数域信噪比的变化如图11所示。从图11中可以看出，当干扰目标能量有限时，对感兴趣目标的深度估计误差影响较小。

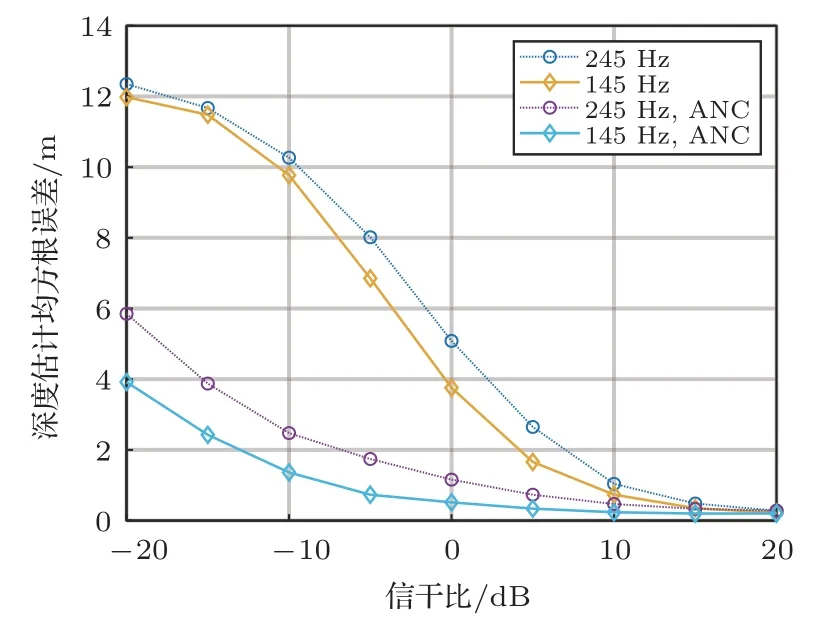
图9 目标深度估计均方根误差随自噪声能量变化Fig.9 The root-mean-square error of target depth estimation varies with the SIR defined by selfnoise

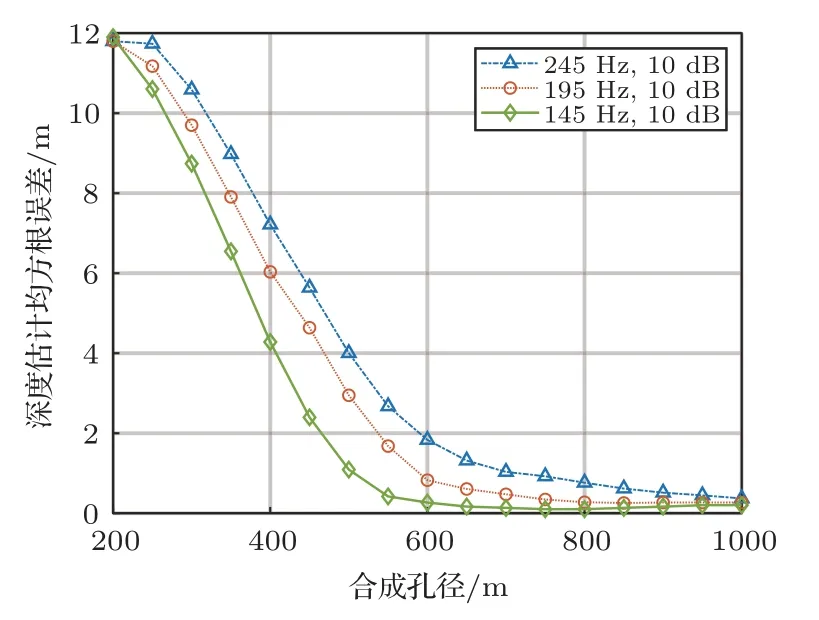
图10 目标深度估计均方根误差随合成孔径变化Fig.10 The root-mean-square error of target depth estimation varies with the synthetic aperture

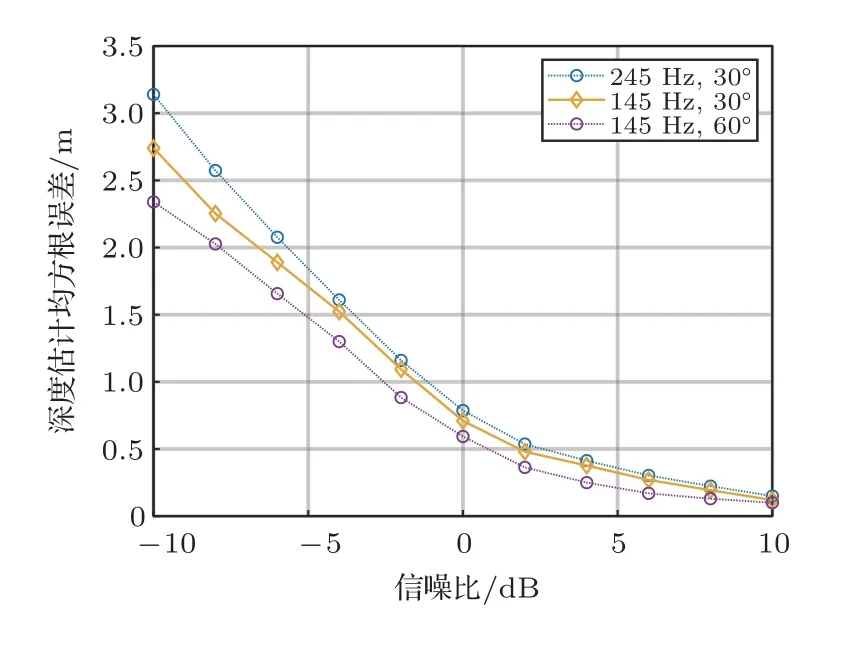
图11 目标深度估计均方根误差随波数域信噪比变化Fig.11 The root-mean-square error of target depth estimation varies with the SNR in wavenumber domain

5 实验数据处理

实验在夏季进行，声速剖面为强负梯度结构，如图12所示。低频声源模拟目标信号频率为165 Hz和195 Hz，声源深度为25 m。拖曳阵阵元数为16，阵元间距为1 m，搭载着拖曳阵的UUV 以1.62 m/s的预设速度背向驶离声源，拖曳阵深度为13 m，初始距离为750 m，数据采集时长为600 s，合成孔径长度为972 m。

195 Hz 信号的相位跟踪和相位抖动估计结果如图13所示，从相位跟踪图中可以看出，实验中UUV的速度不是恒定的，经历了慢速-快速-慢速的变化过程；从相位抖动估计图中可以看出，在实验初始阶段，运动状态较稳定，从250 s 开始出现瞬时随机加速度扰动，450 s 后的50 s 内干扰严重，和快速运动阶段吻合。

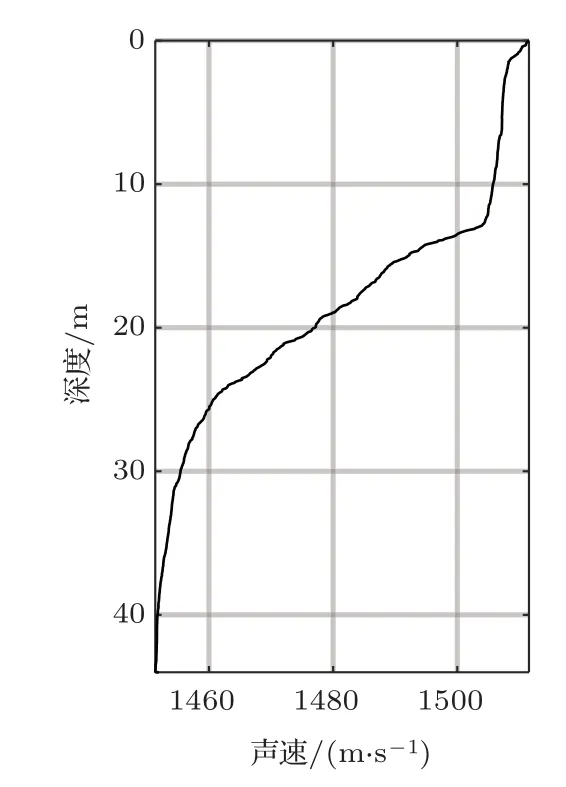
图12 声速剖面Fig.12 Sound speed profile

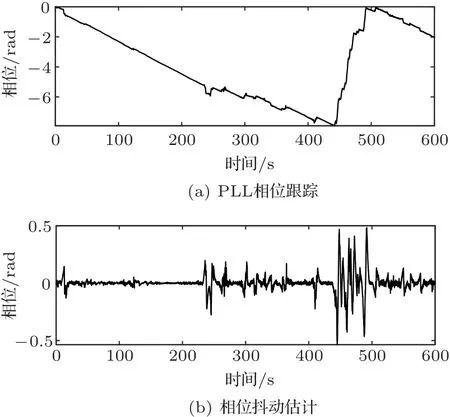
图13 相位跟踪和相位抖动估计Fig.13 Phase estimation and phase jitter estimation

使用SA-SAMV方法和本文提出的稳健方法进行对比，计算的模态估计结果和对应的深度估计结果如图14所示。从图14(a)中可以看出，由于本段数据采集过程中阵列存在明显的速度变化，因此SA-SAMV方法计算的模态波数谱中出现若干伪峰，根据仿真的波数位置提取模态信息并计算的目标深度估计结果显示在图14(b)中，从中可以看出，目标深度匹配度最大值对应深度为30 m，而目标真实深度25 m处仅出现次极大值，目标深度估计存在5 m的误差。

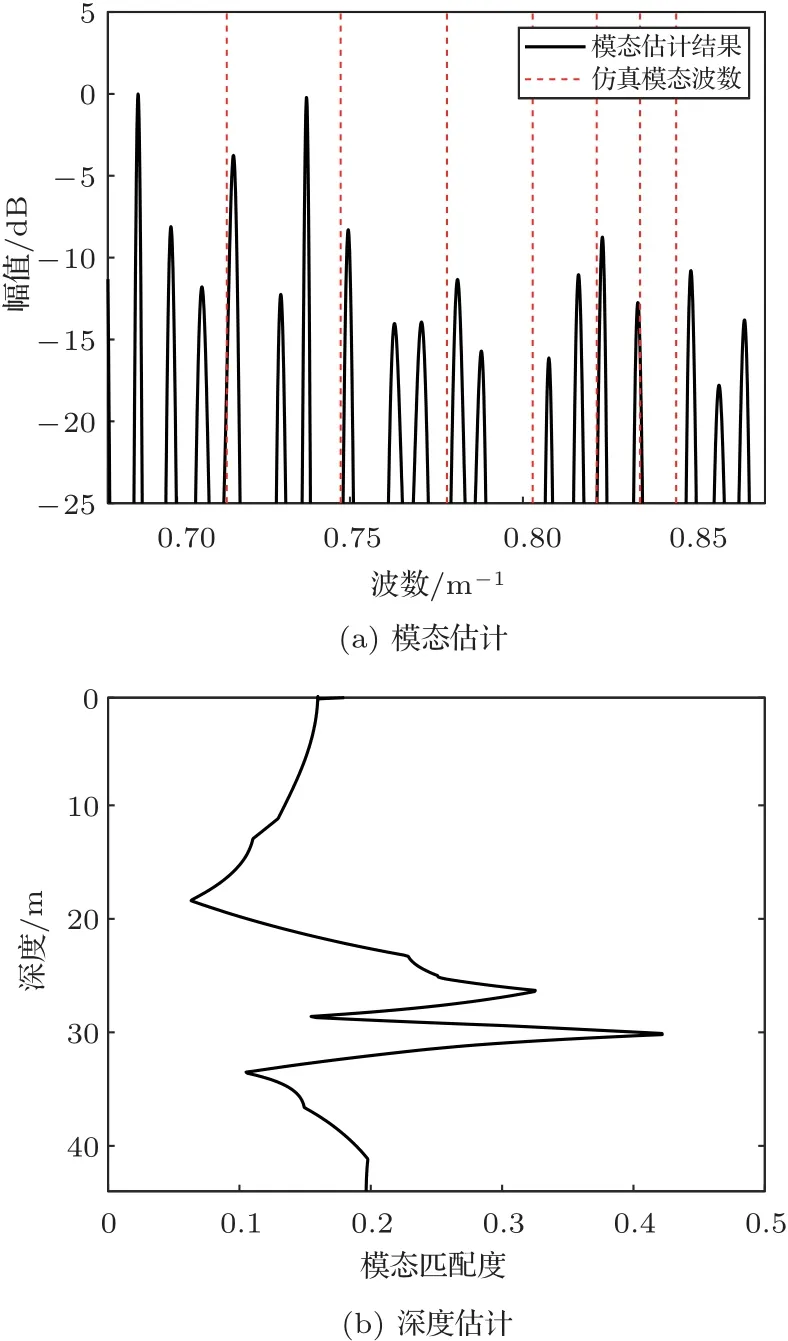
图14 使用SAMV 方法获得的195 Hz 信号的模态估计和深度估计Fig.14 The normalized modal estimation and the target depth estimation for 195 Hz using SASAMV

195 Hz 信号经过抗干扰预处理和未经抗干扰预处理的模态估计结果分别如图15(a)和图15(b)所示，其中红色虚线为仿真模态波数。与之对应的目标深度估计结果如图16所示。从图15(b)中可以看出，由于未进行抗干扰预处理，在第二阶和第三阶模态处未能检测到模态峰值，而在图15(a)中有相对明显的模态能量。从图16(a)中可以看出，经过抗干扰预处理的目标深度估计在25 m 处出现峰值，与真实声源深度吻合，证明了深度估计算法的有效性。在未经抗干扰预处理的图16(b)中，目标深度估计结果准确度下降，具体表现为真实目标深度处峰值不尖锐，且在近水底深度处有较强伪峰。从图15(a)中还可以看出，模态估计波数谱中的峰值位置与理论值并非完全吻合，这是因为实验中无法做到精确测量环境信息，因此仿真的波数位置与实际波数位置存在偏差。在实际应用中，需要在仿真得到的波数位置附近选取距离仿真波数距离较近的峰值进行匹配。另外，模态匹配时阶数选择是一个需要考虑的问题，增加模态匹配的阶数，可以在一定程度上提高目标深度估计分辨率，但同时也降低了估计结果的稳健性，当测量的环境信息与真实环境偏差大时，这种稳健性的下降会带来严重的误差问题。从另一个角度来看，实际上通常对水下目标进行深度估计时，分辨率并不是最主要考虑的性能，因此实际应用中倾向于选择较少阶数的模态进行匹配。

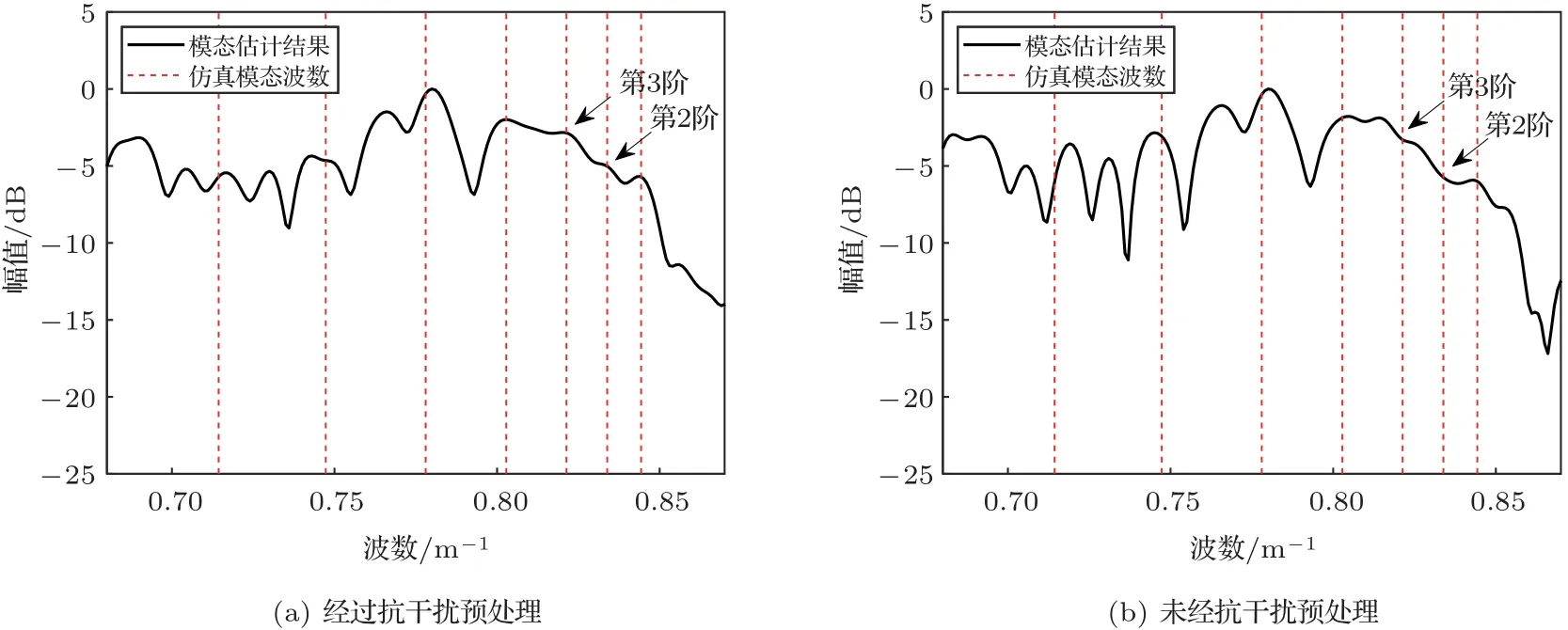
图15 195 Hz 信号的模态估计Fig.15 The normalized modal estimation for 195 Hz tonal signal

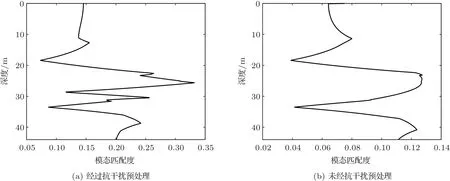
图16 195 Hz 信号的深度估计Fig.16 The target depth estimation for 195 Hz tonal signal

6 结论

本文利用浅海动态声场的传播规律，在简正波模型的基础上提出了一种UUV 拖曳阵被动合成孔径目标深度稳健估计方法，通过基阵的运动获得声场测量的空间增益，在预处理阶段使用FBLMS 算法消除UUV 自噪声干扰，使用二阶锁相环消除阵列随机瞬时加速度干扰。仿真表明，该方法在复杂运动场景下和存在上述两种干扰的环境中的稳健性优于传统方法，声源频率、合成孔径距离和信干比决定了深度估计误差。但在稳健性提升的同时，模态估计的分辨率相比SAMV方法有所下降，需要更大的合成孔径分离模态。最后利用实验数据验证了该方法对水下低频线谱声源的深度估计能力。在后续工作中，将进一步研究模态匹配的阶数选择问题和宽带噪声目标的深度估计问题。