浅海波导中简正波干涉特征频率增强∗

孟瑞洁 周士弘 戚聿波

0 引言

浅海波导中声源被动测距一直是水声学研究的热点问题之一。近些年来，通过对接收信号自相干函数进行时间warping变换算子或波导不变量基的warping 变换，能够获得与声源距离相关联的干涉简正波频率或时延特征。在运动声源的距离估计方面，已提出的利用干涉简正波特征频率[1−2]和干涉简正波延时信息[3]的方法具有非常稳健的性能。然而，在实际海洋环境中，由于环境噪声的影响，接收信号或阵列输出信号具有较低的信噪比，使得信号的干涉简正波特征频谱往往淹没在噪声中，从而影响了被动测距的跟踪性能。

增强信噪比的常见解决思路是时间累积，然而传统的时间累积(例如常规波束形成中的长时间非相干累积)不能有效提高干涉简正波特征频谱的信噪比，这是因为水声信道中存在多途及其频散效应，信号水平纵向相关性不仅限制了时间累积性能，而且较长的时间累积甚至还会平滑或破坏信号原本的干涉结构特征。

针对浅海波导中多途及频散问题，苏晓星等[4]基于声场波导不变性，提出了一种适用于声源频谱缓变条件下提高声场水平纵向相关的频移补偿方法。另外一种思想是直接消除多模频散，王宁等[5]提出了一种类似Fourier变换的双参数消频散变换，利用波导不变量来消除多模频散。warping 变换可以将具有频散的非线性相位信号变为线性相位的准单频信号，可实现不同距离处简正波或者干涉简正波特征频谱的同相叠加，从而获得具有高信噪比的频率特征。在未知目标参数的情况下，本文利用warping变换对阵列输出信号自相关函数进行处理，通过累加不同时刻或距离处干涉简正波的特征频谱来增强干涉简正波的频率特征。

1 基本理论和方法

1.1 阵列输出信号

以L元水平均匀线列阵为例，根据简正波理论，第l个阵元接收到来自远场的信号可以表示为[6]

式(1)中，j 为虚数单位；S(ω)为声源激发频谱；um为第m阶简正波的模态函数；krm为简正波本征值；rl表示第l个阵元到声源的距离，rl=r0+(l-1)dcosθT，式中r0为第一个阵元(参考阵元)到声源的距离，d为阵元间距，θT为信号入射方向相对于基阵轴向的夹角；

根据式(1)中各个阵元接收信号形式，得到常规波束形成器(Conventional beamforming, CBF)的方位谱输出为

其中，参考波数k0=ω/c0，c0是接收深度处的水体声速。

利用常规波束形成得到目标的方位，在目标方位处得到波束形成的阵列输出信号

一定时间内，由波束形成的输出可得到信号的频谱历程，即LOFAR图。在浅海波导中，低频宽带声场往往呈现出明显的干涉条纹特征。然而，这些干涉条纹特征会受到环境噪声以及水体或海底环境变化等因素的影响。另一方面，由于多途效应和频散特性，不同号简正波频散不同，在时频空间上是相互混叠的，且相位呈现不一致的非线性关系，信号存在水平纵向相关性限制，从而导致长时间累积处理不能提供更高的输出信噪比，而且较长的时间累积甚至还会平滑或破坏信号原本的干涉结构特征。

1.2 相干累积处理

针对浅海运动目标，假定运动目标相对基阵的径向速度近似为一个常数。用tri表示第i个时刻信号到达基阵的时间，对基阵波束输出信号自相关函数考虑自相关函数最大峰以右并右移时间tri=ri/c0，得到

其中，kν=krm-krn，Aν(ω)=|S(ω)|2Am(ω)A∗n(ω)，ν表示模态组合数，(m,n)= (1,2)、(2,3)、(1,3)···，V表示模态总数为M的模态组合数，V=C2M。假定波导水平不变且对声场起主要贡献的简正波以海底反射类简正波为主，根据文献[7]的warping变换算子，得到第i个时刻基阵波束输出信号自相关函数的warping变换形式：

真实距离ri下干涉简正波的特征频率µv与假定距离下warping变换频谱干涉简正波的谱峰频率存在关系式[1]

对于运动目标，T时刻基阵波束输出信号自相关函数经warping变换后谱峰频率为

即假定该时间段内初始距离与径向速度之比等于真实距离与径向速度的比值时，warping 变换频谱位置随距离不变，可以实现同相相干累加。在距离未知时，只需求得距离与径向速度的比值即可。

将式(3)反变换到时域，得到第i时刻波束输出的信号形式：

对式(10)的自相关函数Rbi按照式(6)的变换得到

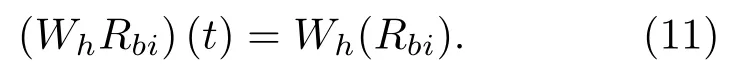
其频谱表示为

式(14)中，SNp表示多拍信号累计warping 变换后频谱能量，S1表示单拍warping 变换后频谱能量，Np表示时间累加的拍数。只有在各个距离点噪声完全不相关的理想情况下(实际不存在)，多个时刻波束输出信号的自相关函数warping频谱相干累加增益才会接近理论计算的时间累加增益10 lg(Np)，但是实际情况中累加warping变换得到的增益往往小于这个理论计算值。

若实际情况中目标方位未知且假定目标所在波束不变，还可以将式(13)的代价函数改为对该段时间初始距离与径向速度比值和目标方位的联合匹配：

综上，利用warping 变换频谱累加对目标信号相干简正波特征频率实现增强的过程如下：

(1)对阵列接收信号进行常规波束形成，得到目标方位角；

(2)对某段距离下目标方位处的波束输出信号自相关函数进行带参数的-warping 变换(假定距离与径向速度)，对变换后频谱进行求和，得到不同参数下式(13)代价函数的分布，根据代价函数的分布得到距离与径向速度的比值；

2 仿真实验

仿真环境参数如下：水深60 m，水中声速1500 m/s。声源深度7 m，频率100～150 Hz，声场接收范围5～10 km，声源运动速度为5 m/s，声源相对于接收阵的入射角为60◦。海底参数如下：海底声速1700 m/s，海底密度1.8 g/cm3，海底吸收系数0.1 dB/λ。32 元等深水听器等间隔布放于59 m 深度，间隔为5 m。图1是接收信号的波束形成以及自相关函数的warping 变换瀑布图，其中图1(b)每个距离点的频谱幅值做了归一化处理，假定warping变换的距离为7 km。图中单阵元输入信噪比-12 dB，噪声为与信号同带宽的高斯白噪声。

假定warping 变换的距离为7 km，对每一次warping 变换的频谱累加300 s，按照式(13)代价函数对进行估计，得到估计值随时间历程的变化如图2所示。其中，黑色点线是根据代价函数的提取值，红色虚线是理论值。可以看出每个时刻的提取值与真实值比较接近，因为实际噪声的影响会导致存在一定的偏差。

图1 CBF 和波束输出信号自相关函数warping 变换后的频谱瀑布图Fig.1 CBF and the spectral after warping transformation of beam output signal autocorrelation function

图2 代价函数 估计值随时间的变化Fig.2 The estimated values of Cost function over time

根据图2的距离与径向速度的比值随时间的分布，得到累加warping 变换的频谱。图3(a)是累加warping 变换的频谱，其中累加时长100 s，每个距离点的频谱做了归一化处理。图3(b)是累加前后warping 变换谱峰频率提取值的对比，对图1(b)中能量最大一组干涉简正波的谱峰频率进行提取结果如图3(b)黑色星线所示，对图3(a)中能量最大一组干涉简正波的谱峰频率进行提取结果见图3(b)红色点线。从图3(b)可以看出，相比于单拍warping变换的结果，累加warping 变换后的谱峰频率方差较小并且在时间上更连续，减小了频率估计与跟踪时的误差。同时累加前后谱峰频率随距离变化的趋势一致，也说明了利用该方法得到的warping 变换后干涉简正波的谱峰频率的可靠性。

图3 -warping 变换频谱与谱峰频率Fig.3 The spectrum of -warping transform and the spectrum peak frequency

接下来说明累加warping变换对干涉简正波进行相干累加的原理。图4(a)和图4(b)分别是单拍warping变换与单拍-warping变换的对比图，假定warping变换的距离都是7 km。从图4(a)可以看出warping 变换后的谱峰频率随假定距离是变化的，这样不能直接相干累加得到高信噪比输出的特征频谱。从图4(b)可以看出-warping 变换的频谱的谱峰频率是一致的，呈现出类似特征频率与距离无关的属性。这样对多拍-warping 变换频谱进行相干累加得到高增益的频谱输出。

图5是累加warping 变换获得的时间增益随快拍数的变化，其中图5(a)阵列输出信噪比是3 dB，图5(b)阵列输出信噪比是6 dB。对比两图可以看出单阵元信噪比较低的情况下，累加warping 变换得到的时间增益是有损失的，在信噪比较高的情况下噪声能量较小，多拍warping 变换得到增益越接近理论计算值。

图4 warping 变换与-warpingFig.4 warping transform and -warping transform

图5 时间增益Fig.5 The time gain

3 实验数据分析

利用2005年中国科学院声学研究所在北黄海浅海海域的一次海底水平阵声学测量实验对方法进行验证，声源能量集中在50～350 Hz。实验海区水深约30 m，接收阵由48 元座底阵组成，其中有效阵元个数为43个，阵元间距1.5 m左右。

图6(a)和图6(b)分别是对阵列接收信号进行处理得到的常规波束形成与波束输出信号自相关函数的warping 变换频谱瀑布。其中图6(a)中出现在100◦～120◦附近的是运动声源，出现在250◦～350◦的是强干扰。根据图6(a)的目标方位角，对阵列接收信号进行目标方位的波束输出得到波束输出信号经warping变换后的频谱如图6(b)所示，其中假定warping变换的距离为7 km，图中每一距离处的warping变换频域信号做了归一化处理。

图6 CBF 和阵列输出warping 变换频谱Fig.6 CBF and warping transform spectrum of array output signal

图7是对实验数据处理得到代价函数和累加warping变换频谱瀑布，假定warping变换的距离为7 km。对目标方位的波束输出信号进行式(13)代价函数的计算，代价函数极值点随时间分布见图7(a)，其中warping 变换的累加时长300 s。根据距离与径向速度的比值得到累加warping 变换的频谱见图7(b)，图中warping 变换累加时长100 s。图7(c)是warping 变换谱峰频率的提取值，其中黑色星线和点线是图7(b)中累加warping变换后两组干涉简正波的谱峰频率，红色点线和星线是图6(b)中单拍warping 变换后两组干涉简正波的谱峰频率。可以看出二者谱峰位置吻合，在累加快拍数不大的情况下累加warping 变换并不改变干涉简正波的谱峰位置，说明方法得到的干涉简正波的谱峰频率是可靠的。

图7 的分布、-warping 变换频谱和谱峰频率Fig.7 The distribution of , -warping transform spectrum and spectral peak frequency

为了验证方法对低信噪比接收信号warping变换频谱的改善能力，对实验数据加上与信号同带宽的高斯白噪声，信噪比-7 dB。降低信噪比后的波束形成结果如图8(a)所示，图8(b)是在图8(a)中目标方位处波束输出信号经warping变换后的频谱，假定warping 变换的距离为7 km。图8(c)是随时间的分布，其中红色点线是测量值，黑色星线是提取值，累加时长300 s。根据的分布，得到累加warping 变换频谱如图8(d)所示，其中累加时长100 s，相比于图8(b)单拍warping变换的结果，可以看出干涉简正波的特征频率结构更加清晰，信噪比得到了有效提升。图8(e)是两组干涉简正波谱峰频率的提取值，其中红色点线与星线是单拍warping变换干涉简正波谱峰频率的提取值，黑色点线与星线是累加warping 变换干涉简正波谱峰频率的提取值。从图8(e)中两组干涉简正波谱峰频率的提取值可以看出，累加warping 变换得到的干涉简正波谱峰频率离散程度较小，能有效地提高距离估计的准确度。

图8 实验数据加噪声的结果Fig.8 The result of experimental data plus noise

4 结论

利用warping算子对目标方位上常规波束形成输出的信号自相关函数进行变换，根据干涉简正波特征频率的不变性通过搜索距离和径向速度的比值对齐不同时刻或距离处warping 变换后的频谱，从而相干累加多拍warping变换频谱获得较高的输出信噪比。本文通过仿真实验和2005年北黄海浅海海域实验数据对算法进行了验证，该方法有效增强了运动声源的warping 变换特征频谱，有利于后续特征频率的利用。

致谢非常感谢2005年出海的所有人员，辛苦采集了数据，为本文的理论提供了支撑。