南中国海海域存在孤立子内波条件下的声场统计特性∗

张青青 李整林 秦继兴

0 引言

内波是海洋环境中普遍存在的一种动力学现象，可导致海水声速剖面随时间和空间变化，进而引起水下声信号的散射，并造成声能量的起伏和声场时间相关半径下降等现象[1−5]。文献[2]通过大陆架海域实验验证了孤立子内波对声波的共振散射作用，数据分析发现声传播损失(Transmission loss,TL)和频率响应的异常，指出在某些频率下孤立子内波可导致20 dB 以上的声信号衰减。文献[3]分析了中美联合远黄海实验中内波条件下的数据，通过与理论模拟结果对比说明了实验观测的声强起伏主要由内波引起。文献[6]概述了SWARM’95 浅海内波声散射实验，研究了在大西洋中部海岸线大陆架由线性内波和非线性内波引起的声传播和散射现象。有学者通过数值模拟发现孤立子波包很大程度上受到耦合简正波模式的强烈影响，并利用耦合简正波模型统计分析了随机声速扰动时声波强度和模态幅度的统计特性[7−8]。随着对内波研究的深入，学者们的研究兴趣逐渐从二维声场和声速场问题转移到三维问题。文献[9-10]分别证实了孤立子内波引起的三维声场效应和水平折射现象。文献[11]指出当声线遇到孤立子内波时对主动声呐探测会产生影响。文献[12] 利用SW’06浅海实验数据研究了非线性内波波包经过声传播路径时的水平折射和多途干涉现象，并给出了这种多途干涉的物理机制。

在国内，宋俊等[13]研究了浅海孤立子内波对声场水平纵向相干特性的影响，但是仿真时采用的是二维模型，没有考虑横向耦合的三维声传播问题。文献[14-15]研究了线性内波和孤立子内波对匹配场时间相关和声场时间相关半径的影响规律。王宁等[16]利用2005年黄海内波起伏实验数据分析了内波、潮汐导致的简正波幅度起伏及其深度分布。李整林等[17]分析了孤立子内波引起的高号简正波到达时间起伏。秦继兴等[18]说明了当孤立子内波的波阵面与声传播路径角度较大时简正波耦合是导致声能量起伏的主要因素，并研究了浅海中孤立子内波引起的声能量起伏规律。

以上大多数研究主要集中于孤立子内波与声场的相互作用，由于实验数据的匮乏，一些研究仅限于理论分析与定性描述，缺乏定量分析和规律性的总结，对于浅海孤立子内波存在条件下声场起伏统计特性的研究鲜有报道。本文利用在南中国海海域实验获取的水文和声场数据，结合二维平流模型重构出与实验水文接近的内波环境，用蒙特卡洛方法研究了有无孤立子内波经过声传播路径时声传播损失的统计特性。

1 实验介绍

2015年秋季，中国科学院声学研究所在南中国海海域进行了一次浅海低频声传播起伏实验，主要目的是研究内波对声传播的影响。实验采取声源和接收阵位置均固定的定点声传播模式，实验获取了5 天的声学数据和水文数据。实验期间实验设备布放相对位置如图1所示，其中S17 点和O1 点分别为发射潜标和接收潜标布放的位置，同时在S17 点和O1 点不同深度上各安装了由温深(Temperature-Depth, TD)传感器组成的温度链，在H1 点布放1条温度链，由这3 条温度链记录水温随时间的变化。声学及环境测量设备布放位置的坐标及3 条温度链安装的温度传感器个数示于表1。图2给出了接收潜标O1 与发射潜标S17 的布放示意图及声传播路径上S17-O1 的海深变化，可看出在声传播路径上海深变化较缓慢，所以可忽略地形变化对声场的影响。其中，S17-O1距离约为14.8 km。另外，S17-H1距离约为14.4 km，O1-H1 距离约为6.5 km。声源S17点海深约为111 m，O1点海深约为105 m。

图1 实验设备布放相对位置示意图Fig.1 Schematic diagram of the placement of experiment sites

表1 声学及环境测量设备布放位置及安装的温度传感器个数Table 1 Locations and installed temperature sensors for acoustic and environmental measurement equipments

图2 接收潜标O1 与发射潜标S17 的布放示意图及传播路径上的海深变化Fig.2 Layout of the receiving submersible O1 and the transmitting submersible S17 and the water depth on the propagation path

接收潜标O1 由18 元自容式水声信号记录仪(Self-contained underwater sound signal recorders,USRs)组成，USR非等间隔地布放在22～76 m 深度范围内，水听器接收灵敏度为-170 dB，信号采样率为16 kHz。坐底声源S17 位于水下108 m，发射信号为线性调频信号，中心频率为200 Hz，带宽为50 Hz，发射信号时间序列如图3所示，每个信号的发射时长为10 s，每2 个信号为一组，相邻2 个信号间隔为30 s，间隔130 s 后重复发射下一组信号，每组信号总长度为180 s，即发射周期为3 min。

图3 发射的线性调频信号时间序列Fig.3 Time series diagram of the chirp signal

图4 9月13日11:00 至9月17日06:00 期间3 个温度链处温度随时间和深度的变化Fig.4 Temperature from 11:00 on September 13 to 06:00 on September 17 as a function of time and depth at three temperature chains

图4是实验期间连续监测4 天的温度随时间和深度的变化，从上至下依次是S17、H1、O1三个站点从9月13日11:00 至9月17日06:00 期间的温度随时间和深度的变化，可看出实验期间在传播路径上存在大振幅孤立子内波和小振幅线性内波。为了计算孤立子内波的波前速度，从图4三个温度链中选取典型的温度剖面并且局部进行放大，图5为选取的9月13日11:00 至9月14日11:00 的温度随时间和深度的变化，可看出在一定的时间段内存在较强的孤立子内波，温度变化幅值较大。根据图5中3个箭头标注的第一个孤立子内波依次经过3 个站点的时间，可估算出该孤立子内波波前的传播速度值平均为0.77 m/s，内波的相对速度方向(红色箭头表示)与3 个温度链的位置如图1所示，与传播路径S17-O1的夹角θ为11◦。

图5 9月13日11:00 至9月14日11:00 之间3 个温度链处温度随时间和深度的变化Fig.5 Temperature from 11:00 on September 13 to 11:00 on September 14 as a function of time and depth at three temperature chains

2 二维平流模型

由于海水声速远远大于海流速度，可采用二维平流模型进行数值仿真，利用温度链长时间测量的水文数据可重构声场仿真所需的动态声速场。由于二维平流模型能够较好地保留温度链数据的特征，与当时声传播路径上的内波环境较为接近，所以可利用该模型获得数值仿真结果，有利于更好地分析实验获取的声学数据。

假设多个温度链垂直布放在声传播路径上的某些固定位置，并长时间记录各自位置处水文数据。采用二维平流模型将固定位置处随时间变化的温度剖面转化为任意时刻声传播路径上随距离变化的声速场，需要两步操作可以完成：首先，使用声速经验公式将温度链处的温度、盐度、压力随时间和深度变化的数值转换为该处随时间和深度变化的声速；其次，假设在声传播路径上声速剖面以固定速度平流输送经过温度链。

第一步，计算声速的经验公式可表示为[19]

其中，c0为参考声速，∆cT、∆cS、∆cP、∆cSTP分别表示与温度T(◦C)、盐度S(‰)、深度H(m)、温盐深相关的量。

第二步，得到各温度链处各个时刻的声速剖面后，再根据声传播路径上计算的孤立子内波的传播速度，采用线性变化将声速剖面转化为沿声传播路径上随距离r变化的声速场，其中距离r为

其中，r表示声传播路径上的距离，t表示时间，t0表示内波到达某一温度链的时间点，r0表示某一温度链的位置，v是孤立子内波在声传播路径上的速度。则在t时刻声传播路径上r距离处的声速剖面可通过式(2)与温度链r0点t0时刻的声速剖面对应起来。实验中，取温度链O1 点为参考点，即r0=0 m；温度链S17 点处，r0= 14.8 km，由温度链数据计算得到的声传播路径S17-O1 上孤立子内波的平流速度为v=0.77 m/s，将以上参数代入式(2)可得到不同时刻声速场的空间分布。作为例子，图6给出了根据S17 点上的温度链数据得到的9月13日15:24:29时刻的声速场空间分布。

图6 根据S17 点温度链数据得到的9月13日15:24:29 时刻的声速场空间分布Fig.6 Spatial distribution of the sound speed field based on the S17 site at 15:24:29 on September 13

3 孤立子内波存在条件下的声场统计特性

利用温度链数据结合二维平流模型重构出随时空变化的海水中声速场分布后，可代入二维抛物方程声场模型[20](RAM-PE)计算内波存在条件下不同时刻的声场。由于声波速度远远大于孤立子内波的传播速度，声信号传播至接收潜标的时间内，内波的传播距离极为有限，所以可将内波场视为准静态，使用RAM-PE模型结合海底参数模型计算声传播路径上孤立子内波存在时水平变化环境下的声场，并分析该声场统计特性。

计算声场的环境参数为图7所给的两层液态海底参数示意图。其中，海深约为110 m，声传播路径上海底地形变化如图2所示。两层液态海底模型中：沉积层厚度为8 m，声速为1595.5 m/s，密度为1.7 g/cm3，衰减系数为0.517(f/1000)1.07dB/λ；半无限大基底层的声速为1704 m/s， 密度为1.9 g/cm3，衰减系数为0.517(f/1000)1.07dB/λ[21]。海水吸收系数可用式(3)表示[22−23]：

其中，频率f的单位为kHz。

数值模拟计算时，选取声源中心频率为200 Hz，声源深度为108 m。采用RAM-PE模型可仿真得到不同深度与距离下的声压值，然后利用声压值求得声强，在1/3 倍频程带宽内对多个频点的声强进行窄带平均，得到多个频点的平均声强：

其中，M为频点个数。本文以窄带平均的传播损失(dB re 1 m)表示声场计算的数值结果：

最后采用蒙特卡洛方法对模型计算的TL 进行统计分析，可获得概率统计结果。将接收点的TL数据每隔1 dB分为一组，计算出每组的概率。假设TL0表示某个样本区间的中点，例如，当样本组区间范围为[70 71]时，TL0=70.5 dB。

图7 南中国海海域两层液态海底参数设置Fig.7 Two-layer liquid bottom parameter settings in the South China Sea

各区间范围内概率计算公式由式(6)给出[24]：

其中，Pi(TL0)表示各区间范围内的概率值，Ni(TL0)表示各区间范围内的样本数，N表示总样本数。

利用模型计算时选取声源深度位于跃层下和接收深度位于跃层上(记为“下发上收”)、声源深度位于跃层下和接收深度位于跃层下(记为“下发下收”)的两种典型情况进行比较分析。下面将分别考虑声传播路径上是否有孤立子内波经过的两种情形，分别对声传播损失进行统计特性分析。

由图5可看出，在9月13日12:30-17:32 时间段内存在线性内波的同时存在大幅度孤立子内波；而在9月13日23:30-14日5:32 时间段内主要存在小振幅线性内波，所以选取这两个时间段内传播路径上的声速剖面进行声场仿真。图8给出了这两个时间段内O1 位置处各个时刻的声速剖面，其中，图8(a)为9月13日12:30-17:32 时间段内传播路径上有孤立子内波经过时的各时刻的声速剖面；图8(b)为9月13日23:30-05:32 时间段内传播路径上无孤立子内波经过时的各时刻的声速剖面。对比图8(a)和图8(b)可知，当孤立子内波经过声传播路径时，声速剖面变化幅度相对较大，跃层深度上下波动较大。

图8 两个时间段内有无孤立子内波经过O1 位置时各时刻的声速剖面Fig.8 Sound speed profiles presence or absence of soliton internal waves in different time periods

3.1 传播路径上有孤立子内波经过

在9月13日12:30-17:32时间段内，传播路径上有大幅度孤立子内波经过。根据温度链数据可重构S17-O1 声传播路径上有孤立子内波经过时的声速剖面空间分布。图9是根据二维平流模型重构的任意两个时刻有孤立子内波经过声传播路径时的海水声速场分布。图10是对应这两个时刻有孤立子内波经过声传播路径时传播损失的空间分布，其中声源深度为108 m，中心频率为200 Hz。

图9 有孤立子内波经过声传播路径时两个时刻的声速场空间分布Fig.9 The spatial distribution of the sound speed field when the soliton internal waves entering the sound propagation path

图10 有孤立子内波经过声传播路径时的传播损失二维伪彩图Fig.10 Two-dimensional diagram of the TL of soliton internal waves entering the sound propagation path

图11给出了模型计算的有孤立子内波经过声传播路径时间段内的不同接收点处声传播损失随时间变化的曲线，其中声源深度为108 m，中心频率为200 Hz，收发距离为14.8 km。图11(a)为“下发上收”的结果，接收深度为22 m；图11(b)为“下发下收”的情况，接收深度为76 m。从图中可看出，接收点声传播损失随时间呈一定的准周期性起伏振荡。由于海洋环境中同时存在线性内波和孤立子内波，所以周期性并不是十分明显，当只有孤立子内波存在时，将会呈现明显的周期性变化[18]。在图11(a)中声传播损失起伏最大可达到7 dB，图11(b)中声传播损失起伏最大可达到8 dB。

图11 传播路径上有孤立子内波经过时不同接收点处声传播损失随时间变化的曲线Fig.11 Curve of the TLs when soliton internal waves entering the sound propagation path at each receiving point

3.2 传播路径上无孤立子内波经过

在9月13日23:30-14日5:32 时间段内，传播路径上主要存在小振幅的线性内波，无大幅度孤立子内波。图12是根据二维平流模型重构的任意两个时刻无孤立子内波经过声传播路径时的海水声速场分布。图13是对应这两个时刻无孤立子内波经过声传播路径时的传播损失空间分布，其中，声源深度为108 m，中心频率为200 Hz。

图14给出了模型计算的无孤立子内波经过声传播路径时间段内的各个接收点处声传播损失随时间变化的曲线，其中声源深度为108 m，中心频率为200 Hz，图14(a)为“下发上收”的结果，接收深度为22 m；图14(b)为“下发下收”的结果，接收深度为76 m。从图中可以看出，接收点声传播损失随时间无规则起伏振荡。在图14(a)中声传播损失起伏最大约为3 dB，图14(b)中声传播损失起伏最大约为4 dB。

图12 无孤立子内波经过声传播路径时两个时刻的声速场空间分布Fig.12 The spatial distribution of the sound speed field when there are no soliton internal waves entering the sound propagation path

图13 无孤立子内波经过声传播路径时的传播损失二维伪彩图Fig.13 Two-dimensional diagram of the TL when no soliton internal waves entering the sound propagation path

比较图11和图14可知，当孤立子内波在声传播路径上移动时，接收点在短时间内声传播损失起伏剧烈，声传播损失起伏最大相差可达7～8 dB；而无孤立子内波经过声传播路径时，接收点声场能量起伏相对较小，最大相差为3～4 dB。文献[18]和文献[25]指出，当孤立子内波经过声传播路径时，引起声能量起伏与内波波阵面和声传播路径所成角度有关，当角度较大时不同号简正波耦合是引起声能量起伏的主要因素。

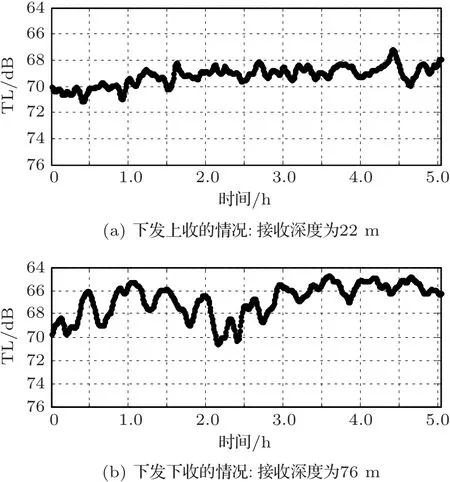
图14 声传播路径上无孤立子内波经过时不同接收点处声传播损失随时间变化的曲线Fig.14 Curve of the TLs when no soliton internal waves entering the sound propagation path at each receiving point

同时，当声源位于跃层下时(海底附近)，接收位置不同，孤立子内波对声场的影响也不同。对下发上收和下发下收的两种情况进行声场统计特性分析，利用式(4)～(6)可以数值计算声传播损失概率统计结果。图15给出了模型计算的接收深度位置不同时的声传播损失的概率分布，其中声源深度为108 m，中心频率为200 Hz，收发距离为14.8 km，这里计算区间概率时总样本数取值为N= 600。图15(a)表示“下发上收”的情况，即接收器位于跃层上，接收深度22 m；图15(b)表示“下发下收”的情况，即接收器位于跃层下，接收深度76 m。进行声场统计特性分析时，TL 概率分布在一定的区间范围内，且最大概率对应的TL在区间中间，所以可用概率分布的区间宽度衡量TL 的分散程度。从图15中可以看出，在有无孤立子内波经过时，图15(a)为接收器位于跃层之上时(下发上收)，TL概率分布区间宽度分别为9 dB 和7 dB；图15(b)为接收器位于跃层之下时(下发下收)，TL 概率分布区间宽度分别为12 dB 和7 dB，说明孤立子内波经过声传播路径比不经过声传播路径条件下的TL 概率分布更加分散。

图15 模型计算的不同接收深度的声传播损失的概率分布Fig.15 The probability distribution of the TLs at different receiving depths calculated by the model

图16给出了实验期间有无孤立子内波经过声传播路径时的两个时间段内不同接收深度的声传播损失的概率分布，其中声源深度为108 m，中心频率为200 Hz，收发距离为14.8 km，这里计算区间概率时总样本数取值为N= 200。对比图16(a)和图16(b)，也可得到与数值结果类似的结论，“下发下收”比“下发上收”的TL概率分布更加分散。

图16 实验期间不同接收深度的声传播损失的概率分布Fig.16 The probability distribution of the TLs at different receiving depths during the experiment

4 结论

利用南中国海浅海海域一次低频声传播起伏实验数据估计了孤立子内波波前速度，并且结合二维平流模型重构出接近实验水文的动态声速场，使用RAM-PE 模型结合Monte-Carlo 方法分析了有无孤立子内波经过声传播路径时的声场统计特性。模型计算和实验结果表明：对于同一个收发声系统，声传播路径上有孤立子内波比无孤立子内波情况声传播损失起伏更加剧烈、声场概率分布更加分散；对于同一个发射声系统，接收声系统分别位于跃层上下方，“下发下收”比“下发上收”情况传播损失的概率分布区间更加分散。

致谢感谢参与2015年秋季南中国海调查实验的全体“实验1”工作人员，是他们的辛勤劳动为本文提供了高质量的实验数据。