当导数遇上三角
2020-03-02林国红
林国红
函数与导数问题是高考压轴题的常客,也是整套试题中的重头戏,是最具区分度的亮丽风景所在.随着高考命题的深入开展,导数压轴题的命制并没有走入桎梏,反而涌现出越来越多的典型、新颖的考题.
2019年全国卷Ⅰ文科和理科的函数与导数问题是与三角函数交会的题型,引起师生的较大反响,这类试题可谓多姿多彩,也常考常新.由于三角函数有其独特的性质,且表达式中含有三角函数无论怎么求导,都会出现含三角函数,从而使问题的后续求解较为困难.因此,如何破解这类函数与导数问题是教师和学生面临的一大难题.本文笔者以近年高考或模拟考试中与三角函数有关的试题为例,进行分类解答,供读者参考,希望能抛砖引玉,提高读者复习效率.
1 函数的极值点与零点问题

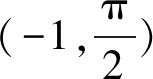
(2)f(x)有且仅有2个零点.

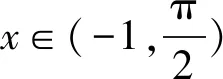
(2)易知f(x)的定义域为(-1,+∞).
① 当x∈(-1,0]时,由(1)知,f′(x)在(-1,0)单调递增,而f′(0)=0,所以当x∈(-1,0)时,f′(x)<0,故f(x)在(-1,0)单调递减,又f(0)=0,从而x=0是f(x)在(-1,0]的唯一零点.

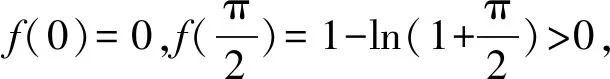

④ 当x∈(π,+∞)时,ln (x+1)>1,所以f(x)<0,从而f(x)在(π,+∞)没有零点.
综上,f(x)有且仅有2个零点.

(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.

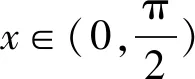
(2)由题设知f(π)≥aπ,f(π)=0,可得a≤0.由(1)知,f′(x)在(0,π)只有一个零点,设为x0,且当x∈(0,x0)时,f′(x)>0;当x∈(x0,π)时,f′(x)<0,所以f(x)在(0,x0)单调递增,在(x0,π)单调递减.
又f(0)=0,f(π)=0,所以当x∈[0,π]时,f(x)≥0.又当a≤0,x∈[0,π]时,ax≤0,故f(x)≥ax.因此,a的取值范围是(-∞,0].

2)要求证一个函数有且只有一个零点,可先用函数零点的存在性定理证明函数存在零点,再证明函数为单调函数.求证函数零点的唯一性,其依据是如果函数f(x)在区间[a,b]上是单调函数,并且f(a)·f(b)<0,则函数f(x)在区间(a,b)上至多有一个零点.如果要证明函数有多个零点,一般要将区间进行分类讨论.此类题型考查导数的综合应用,涉及函数的单调性、函数的零点等多个知识点,综合考查函数与方程、转化与化归、分类讨论等思想.
2 函数的极值与最值问题

(1)求曲线y=f(x)在点(0,f(0))处的切线方程;


(2)设h(x)=f′(x)=ex(cosx-sinx)-1,则
h′(x)=ex(cosx-sinx-sinx-cosx)=-2exsinx.
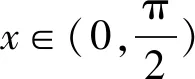


(1)若a≤1,证明:f(x)是定义域上的增函数;
(2)是否存在a,使得f(x)在x=0处取得极小值?说明理由.


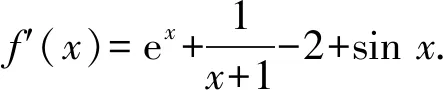
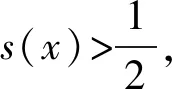
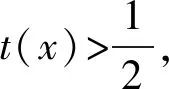
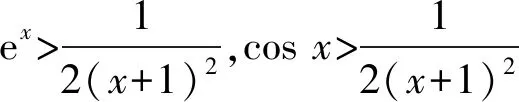
因此,存在a=2,使得f(x)在x=0处取得极小值f(0)=0.

3 证明函数不等式

(1)若函数f(x)存在极小值点,求m的取值范围;
(2)证明:f(x+m) (2)当m≤0时,有f(x+m)=xln (x+m)≤xlnx,若xlnx ① 若x∈(0,1],则ex+cosx-1>0,xlnx≤0,所以xlnx 综上,f(x+m) (1)若x=x0时,f(x)取得极小值f(x0),求实数a及f(x0)的取值范围; (2)当a=π,0 s(x)>s(π)=1+mln π>1. (1)求证:f(x)≤0; 由上述例子可看出,导数与三角函数交会的问题题型众多,函数的表达式多是三角函数与ex,lnx相结合,主要考查函数的单调性、零点、极值与最值、恒成立等问题.由于三角函数的特殊性,所以试题不仅考查导数公式和导数的运算法则,还考查三角函数中的恒等变换(倍角公式,化一公式等)、周期性、有界性、常见的三角不等式等.思想方面主要考查转化与化归、方程与函数、数形结合、以直代曲等.总之,这类问题综合考查考生逻辑思维、转化、推理与运算等能力,综合度较高,对于考生运用所学知识,寻找合理的解题策略以及推理论证能力有较高的要求. 因此,在复习备考中要注重突出主干知识,导数试题注重对导数的几何意义、运算法则、导数在研究函数中的应用等方面进行考查.函数单调性是核心,要深化对函数单调性的认识,复习时需注重导数法在函数单调性中的应用.同时,还需注重变式训练,注意揭示解题规律,归纳提炼方法,即复习时要善于总结,将涉及三角函数的导数试题分类探究,并归纳出常用的解法与注意事项.变式训练可以有效地培养学生思维的灵活性和创造性,而归纳反思则可把解题的思想方法纳入自己的知识系统,举一反三,触类旁通.
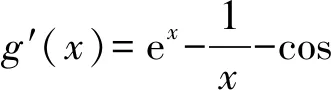
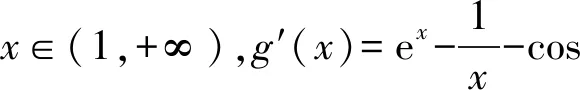



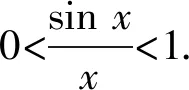

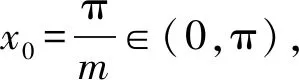
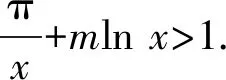

4 恒成立问题