如何应对导函数的“隐零点”

李连海 张艳利

函数的“隐零点”是指客观存在,但无法直接求出的零点．导数法是求解或证明不等式恒成立问题的常用工具,即通过构造函数,将所求问题转化为求目标函数的最值问题.求最值的关键是判断函数的单调区间,而导函数的零点往往是函数单调区间的分界点,因此，导函数零点的求解就显得至关重要．但对于“隐零点”同学们往往一筹莫展.本文通过“构造函数、利用导数”解决一道不等式证明问题为例,提出几种应对“隐零点”的策略,供读者参考．

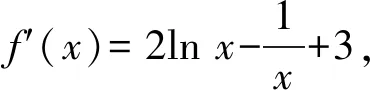
1 放缩函数

证明因为x≥lnx+1(x>0)(在应用此不等式时,应先给出证明,此处略),所以f(x)=(2x-1)·lnx+x≥(2x-1)lnx+lnx+1=2xlnx+1．

2 设而不求

对函数f(x)求导后,能够判断出导函数存在零点,但无法直接求解时,可利用“设而不求”法,即设导函数的零点为x=x0,而进一步可判断出函数f(x)在x=x0取得最值,此时可将f(x0)与f′(x0)=0联立,求其最值．

①

在区间(0,x0)内,f′(x)<0,f(x)单调递减;在区间(x0,+∞)内,f′(x)>0,f(x)单调递增．所以

fmin(x)=f(x0)=(2x0-1)lnx0+x0.

②

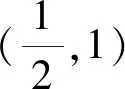
又因为h(1)=0,所以h(x)>0,即f(x0)>0，所以f(x)>0.

3 找关键点

当x∈(1,+∞)时,2x-1>0,lnx>0,故(2x-1)lnx+x>0恒成立;

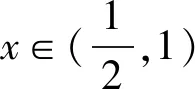
4 分离函数

若采用直接法构造后,所得函数的导函数零点不易求得,则可考虑将所证不等式转化为两个熟悉的函数,分别求函数的最值．

5 转化函数

若函数中含有lnx与其他函数相乘或相除的项,直接求导,则导函数中仍含有lnx,不易求出导函数的零点．因此可考虑先将lnx“独立”出来,再求导．

证明欲证f(x)=(2x-1)lnx+x>0,

①

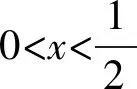
综上所述，f(x)>0恒成立．

综上所述,处理导函数的“隐零点”问题,可以利用放缩函数、找关键点、设而不求等方法.当然除了上述几种方法,还可以应用直接或间接分析法、二次求导法等,在此不再举例．希望同学们不断归纳总结,以便能够灵活应对导函数的“隐零点”问题．