剖析导数应用中的几个失分点
2020-03-02孙桂琴
孙桂琴
导数是高中数学重点内容,也是研究函数问题的重要工具,但在应用导数时,同学们常常由于对相关概念理解不透彻,造成失分.本文对几个常见的失分点进行举例说明,以期帮助同学们避免类似错误的发生.
1 导数为零的点与极值点的关系不明

错解当x≤0时,f′(x)=3(x+1)2ex+1+(x+1)3ex+1=(x+1)2ex+1(x+4).令f′(x)=0,得x=-4.当x∈(-∞,-4)时,f′(x)<0,f(x)单调递减;当x∈(-4,0)时,f′(x)>0,f(x)单调递增.所以x=-4为f(x)的极小值点.
由条件可知f(x)是定义域为R的偶函数,所以x=4也是f(x)的极小值点,故函数f(x)有2个极值点.
剖析从极值点的定义来看,“导函数为零的点”是“极值点”的既不充分也不必要条件.如f(x)=x3在x=0时,f′(x)=0,但x=0并不是函数的极值点,另外函数极值点处的导数值也有可能不存在.本题中,f′(0)不存在,但x=0是函数的极大值点,故函数f(x)共有3个极值点.
2 忽视曲线“在某点”与“过某点”切线的区别

错解因为点P(2,1)在曲线f(x)上,求导得f′(x)=3x2-4x,f′(2)=4,所以过点P(2,1)处切线方程是4x-y-7=0.
剖析本题所给的点P(2,1)虽然在曲线f(x)上,但题目所求的是过点P(2,1)的切线,所以点P(2,1)并不一定是切点.
设切点坐标为(x0,y0),则
①

3 非等价变形



在区间(-∞,2)内,g′(x)>0,g(x)单调递增;
在区间(2,+∞)内,g′(x)<0,g(x)单调递减.
综上所述,x=2是函数g(x)的极大值点,g(2)=-e2,故a>-e2,即实数a取值范围是
(-e2,0)∪(0,+∞).
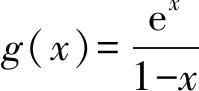
当x=1时,f(1)=1≠0,所以f(x)没有零点.
当x≠1时,在区间(-∞,1)∪(1,2)内,g′(x)>0,g(x)单调递增;在区间(2,+∞)内,g′(x)<0,g(x)单调递减.
又因为在(-∞,1)内,g(x)>0,所以函数f(x)没有零点时实数a的取值范围是(-e2,0).
4 过程不严谨

(1)若x=2为f(x)的极值点,求a的值.

剖析上述解法的错误之处有两点.
1)在第(1)问中求出a的值后,没有检验.

2) 在第(2)问中应用了放缩法,即利用不等式ex≥x+1和x≥lnx+1进行放缩.但在使用这些不等式时,应先给出证明过程,即先证再用.
5 以图代证

(1)若x=2为f(x)的极值点,求a的值;
(2)若f(x)≥0在(0,+∞)恒成立,求a的取值范围.

图1
错解由f(x)=aex-lnx-1,可得
当a≤0时,f′(x)<0,f(x)单调递减,f(1)=ae-1<0,不符合题意.

fmin(x)=f(x0)=aex0-lnx-1.




导数应用中的失分点,不只本文所述的几种类型,希望广大教师要根据不同的题目针对典型错误进行归纳总结,以帮助同学们有效纠错、避错.
