常见两类典型斜面动力学问题归类赏析
2020-03-02杨荣富赵文浩
杨荣富 赵文浩
(陕西省汉中市宁强县天津高级中学 724400)
一、常见两种模型解析
典型问题1 如图1所示一固定在水平面的斜面,物块放在粗糙斜面上当物块沿斜面匀速下滑时动摩擦因数满足什么条件?

解析对滑块受力分析如图2所示.
沿斜面由力的平衡得:f=mgsinθ①
垂直于斜面由力的平衡:N=mgcosθ②
又有滑动摩擦力f=μN③
所以:mgsinθ=μmgcosθ,即:μ=tanθ
典型问题2 如图3所示物块放在光滑斜面上,当物块沿斜面加速下滑时加速度是?
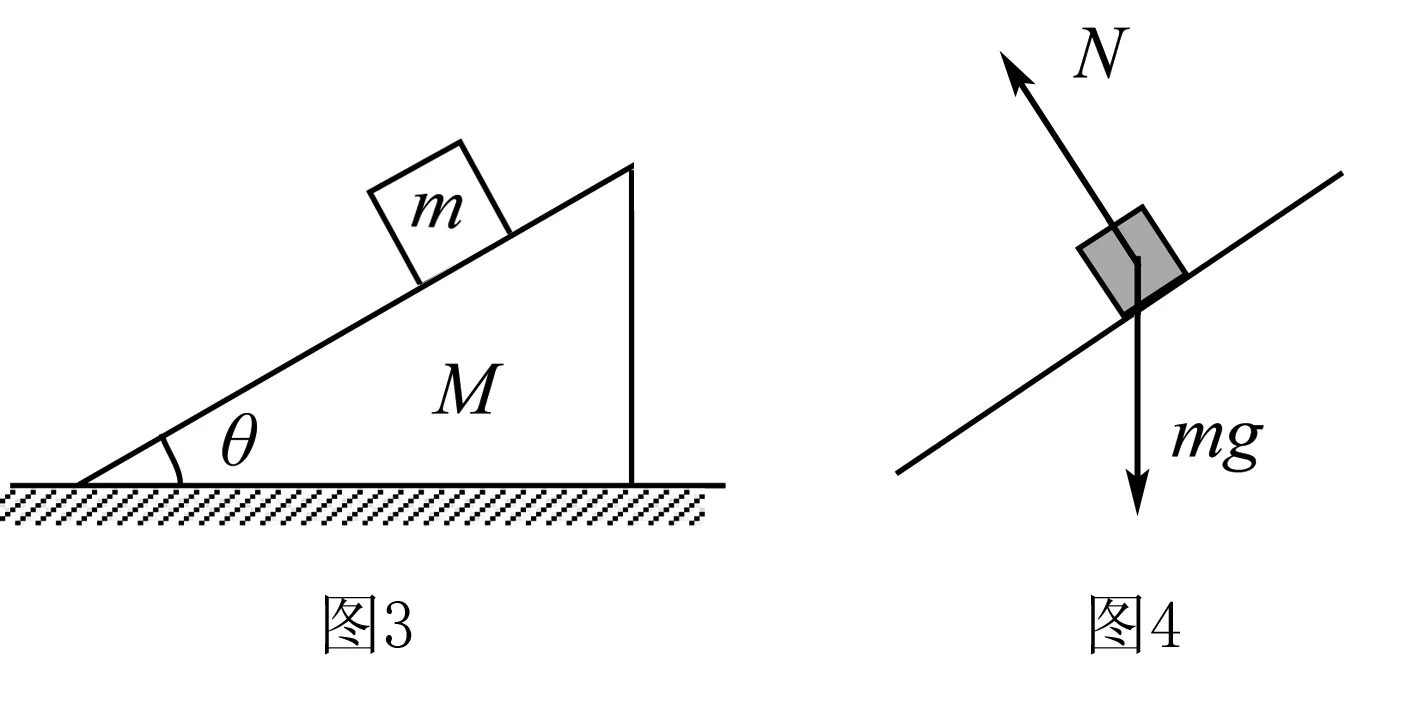
解析对滑块受力分析如图4所示
沿斜面由牛顿第二定律得:mgsinα=ma
解得自由滑行时加速度:a=gsinθ,方向沿斜面向下.
二、高考真题欣赏
例1(2011年安徽理综卷14题)一质量为m的物块恰好静止在倾角为θ的斜面上.现对物块施加一个竖直向下的恒力F,如图5所示.则物块( ).
A.仍处于静止状态 B.沿斜面加速下滑
C.受到的摩擦力不变 D.受到的合外力增大
解析本题考查知识点【典型问题1】,由于质量为m的物块恰好静止在倾角为θ的斜面上,说明斜面对物块的作用力与物块的重力平衡,满足mgsinθ=μmgcosθ斜面与物块的动摩擦因数μ=tanθ.对物块施加一个竖直向下的恒力F,仍满足(mg+F)sinθ=μ(mg+F)cosθ使得合力为零,故物块仍处于静止状态,A正确,B、D错误.摩擦力由mgsinθ增大到(F+mg)sinθ,C错误.
拓展:如果将力F变为竖直向上,物体仍然可以恰好静止.

例2(2013年广东理综卷)如图6所示,物体P静止于固定的斜面上,P的上表面水平,现把物体Q轻轻地叠放在P上,则( ).
A.P向下滑动 B.P静止不动
C.P所受的合外力增大D.P与斜面间的静摩擦力增大
解析本题考查知识点【典型问题1】,由于物块P静止在倾角为θ的斜面上,说明斜面对物块的作用力与物块的重力平衡,满足mpgsinθ≤μmpgcosθ斜面与物块的动摩擦因数μ≥tanθ.加上Q相当于增加了P的质量,不等式两边都增加即(mpg+mg)sinθ≤μ(mpg+mg)cosθ不等式仍然成,则物块P、Q仍然平衡.选BD
三、典型例题欣赏
典型问题1 上表面平行于斜面的叠加问题
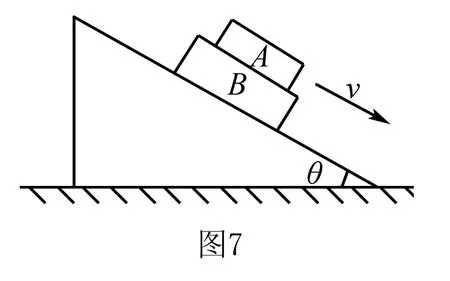
如图7所示,物体A叠放在物体B上,A、B的质量分别为mA、mB,且上、下表面均与斜面平行,它们以共同速度沿倾角为θ的固定斜面C匀速下滑,则( ).
A.A、B间无摩擦力的作用
B.B受到的滑动摩擦力的大小为(mA+mB)gsinθ
C.B受到的静摩擦力的大小为mAgcosθ
D.取走A物后,B物将做匀加速直线运动
解析对A分析,A受到竖直向下的重力,垂直斜面向上的支持力,如果A、B之间没有摩擦力作用,则A的合力不可能为零,即不能做匀速直线运动,所以AB之间有摩擦力存在,为静摩擦力,大小等于A的重力沿斜面向下的分力,即f1=mAgsinθ,故AC错误;将AB看做一个整体,整体受到竖直向下的重力,斜面的支持力,沿斜面向上的摩擦力,即在沿斜面方向上重力沿斜面向下的分力大小等于物体受到沿斜面向上的摩擦力,故有f=(mA+mB)gsinθ,同时根据滑动摩擦力公式有:(mA+mB)gsinθ=μ(mA+mB)gcosθ,即μ=tanθ,只要满足这个关系式即可做匀速直线运动,与质量大小无关,B正确D错误;
典型问题2 上表面平行于斜面的叠加问题
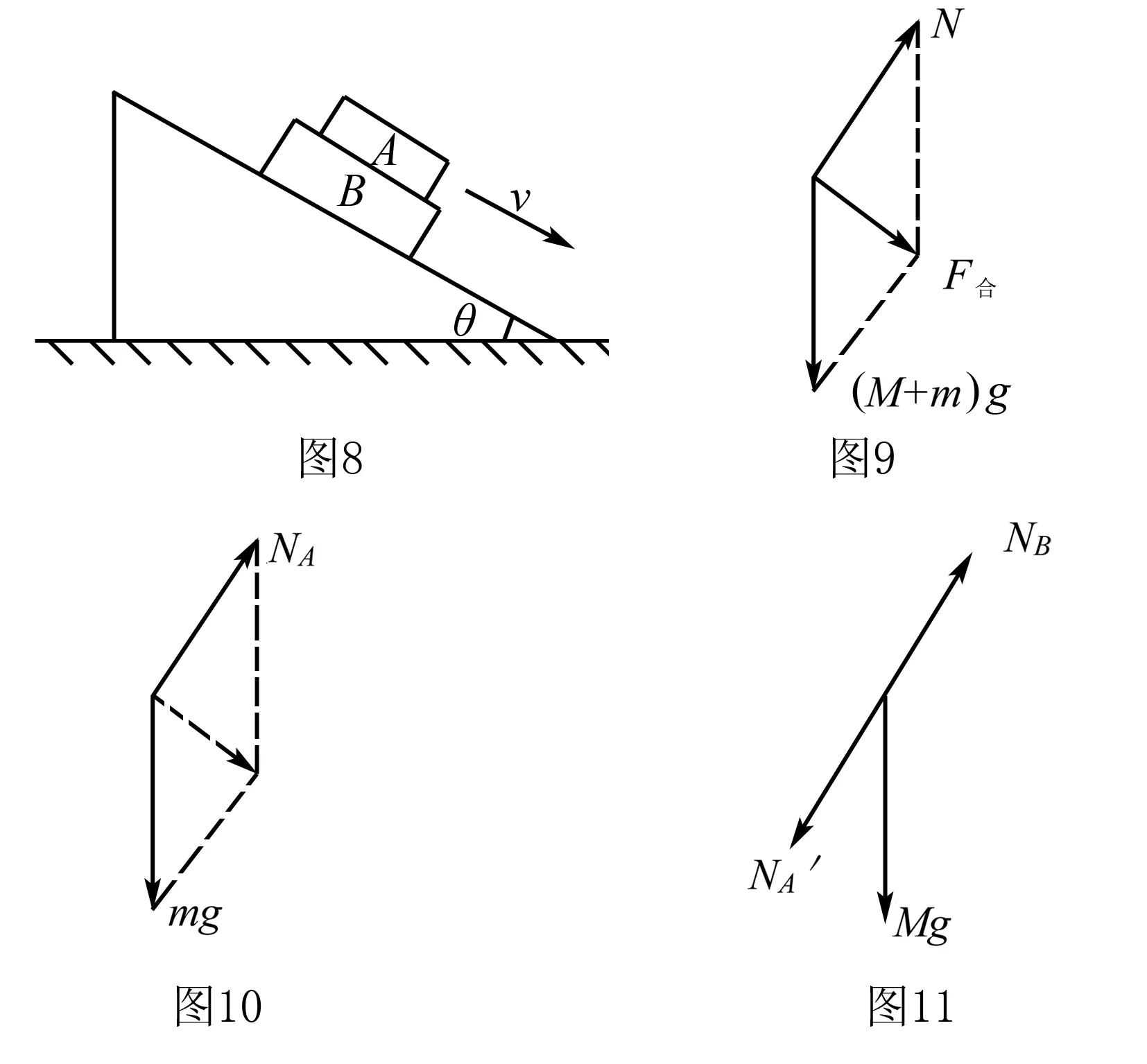
如图8所示,物体A叠放在物体B上,A、B的质量分别为mA、mB,且上、下表面均与斜面平行,它们以共同速度沿倾角为θ的固定光滑斜面加速下滑,试分析A、B加速度及受力情况.
解析A、B有共同加速度,将A、B看成整体受力分析如图9所示:整受到体重力及斜面给物体B的弹力.
由牛顿第二定律有:(M+m)gsinθ=(M+m)a
解得加速度a=gsinθ
如果A与B之间有摩擦力那么A的加速度将不会是a=gsinθ,故A、B之间没有摩擦力,对A受力分析如图10所示.
对物体B受力如11图所示,B将会受到重力Mg、斜面给B的支持力N,A给B的压力NA'.
典型问题1上表面水平的叠加问题

如图12所示,物体B的上表面水平,当A、B相对静止沿斜面匀速下滑时,斜面保持静止不动,则下列判断正确的是( ).
A.物体B的上表面一定是粗糙的
B.物体B、C都只受4个力作用
C.物体C受水平面的摩擦力方向一定水平向右
D.水平面对物体C的支持力小于三物体的重力大小之和
答案:B
典型问题2上表面水平的叠加问题
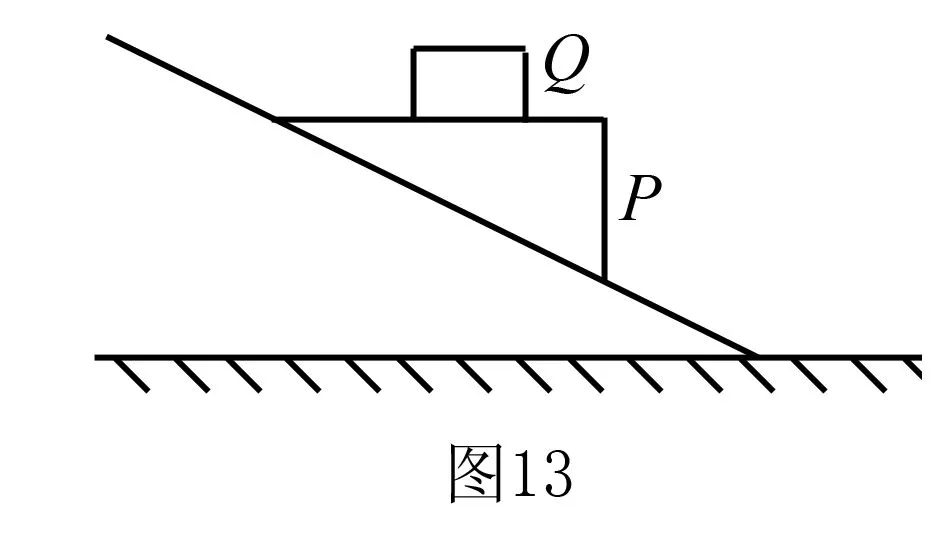
如图13所示,质量分别为m、M的两物体P、Q保持相对静止,一起沿倾角为θ的固定光滑斜面下滑,Q的上表面水平,P、Q之间的动摩擦因数为μ,则下列说法正确的是( ).
A.P处于超重状态
B.P受到的摩擦力大小为μmg,方向水平向右
C.P受到的摩擦力大小为mgsinθcosθ,方向水平向左
D.P受到的支持力大小为mgsin2θ
答案:C
有了上面两种典型问题归类推导,解决这一类问题就游刃有余,这也体现了能力立意的物理理念和物理学科核心素养,因此对该命题的归类总结对学生学习动力学问题起到了很好地帮助.
