基于经验小波变换的基因关联隐私保护实验研究

陈红松，孟彩霞，刘书雨

（1.北京科技大学 计算机与通信工程学院，北京100083；2.铁道警察学院，河南 郑州450053）

致病基因关联分析是全基因组关联研究[1]（Genome-wide Association Studies，GWAS）中的一项分析DNA序列集以发现疾病遗传基础的流行方法，这项研究主要检查特定患者群体的基因中数千个单核苷酸多态性位点（SNP）与疾病之间的相关度，对SNP进行评分，并根据这个评分对相关度较高的SNP排序.但对于GWAS发布的数据而言，即使是只发布统计数据，患者的疾病状态也可以从每个SNP与疾病相关联的统计检验中推断出来，这使得患者的隐私面临着泄露的风险.

目前已有许多研究人员研究使用差分隐私技术来解决这一问题，差分隐私保护技术是当前数据发布中最主要的隐私保护方法，它通过向查询数据中添加噪声来干扰攻击者泄露原始数据的目的，从而达到隐私保护效果.差分隐私保护技术的应用使得数据发布的效率得到了很大的提高，但为了满足差分隐私保护要求需要注入过高的噪声，影响数据的正确性和可用性，最终导致数据效用降低.为了解决这一问题，本文提出了一种基于EWT变换的差分隐私保护方法，不仅依赖于注入噪声，还通过适当过滤部分噪声实现隐私保护与数据可用性的合理折中，由于只是针对噪声的注入、变换和过滤，所以不会还原出用户隐私信息.主要研究目的是在致病基因相关度研究中，使用差分隐私保护患者隐私的同时，降低由于添加差分隐私噪声带来的误差.

1 相关技术

1.1 差分隐私

1.1.1 定义

差分隐私的主要思想是给数据集中的每条记录都添加一个噪声，使在一个数据集上计算的给定统计量的结果类似于在另一个任意的数据集上计算的相同的统计量，以此来把数据泄露的概率控制在一定的范围内，从而达到隐私保护的目的.满足以上两个数据集中最多只有一条记录不同，即如果一个数据库是另一个数据库的正确子集，那么较大的数据库只比另一个多包含一行数据.

本文专注于保护表型数据，因此对差分隐私的定义进行略微修改，如定义1.

定义1[1]设F是一个随机函数，它接受一个n×m的基因型矩阵D和一个n维表型向量y，并输出结果F（D，y），Ω表示随机函数F的输出范围，那么随机函数F对于任意的ε＞0，满足ε-表型差分隐私.对于任意的基因型矩阵D，任意的表型向量y，y′∈{0，1}n（y与y′仅有一个坐标不同）以及任意的输出集合S⊂Ω，我们规定了ε-表型差分隐私：

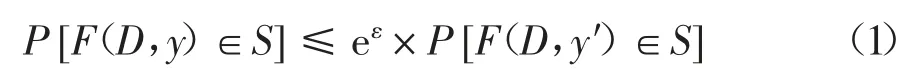
ε为隐私保护预算，由数据拥有者公开定制，ε的值越接近0表示差分隐私保护级别越高，但同时这也意味着F的输出越不准确.

这与差分隐私的通常定义不同，因为在差分隐私中D通常不是固定的，而我们假设基因型矩阵D是固定的.直观地，以上定义表明，当一个人患有疾病时，F返回的结果在统计上与他们没有疾病时返回的结果没有区别.

1.1.2 差分隐私强度影响参数

1）隐私保护预算[2].隐私保护预算ε一般体现了F所能提供的隐私保护程度.因为ε取值越小，隐私保护程度就越高，反之亦然，因此选取多大隐私保护预算，ε是一项非常重要的参数，需要根据具体需求定义ε的取值范围.

2）敏感度[3].敏感度是一个衡量加入噪声量的参数信息，指的是对数据集中任意删除操作对结果所造成的最大改变力度.

定义2全局敏感度（Global Sensitivity）.设有函数f：D→Rd，输入为一数据集，输出为一d维实数向量.对于任意的邻近数据集D和D′，若满足公式（2），

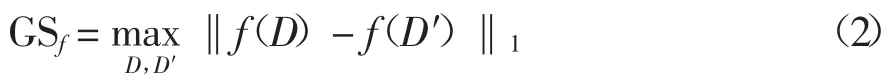
则GSf称为函数f的全局敏感度，全局敏感度用于量化表示对原始数据集D增加或删除一条记录时，对于整个算法f输出结果的最大影响.其中，‖f（D）-f（D′）‖1是f（D）和f（D′）之间的1阶范数距离.函数本身决定了全局敏感度的选取，函数不同，全局敏感度也不相同.

1.1.3 实现机制

面向致病基因相关度研究分析中，差分隐私的实现主要采用3种实现机制，包括拉普拉斯机制、指数机制以及高斯机制.

1）拉普拉斯机制.

定义3拉普拉斯机制（Laplace Mechanism）[4].给定数据集D，设有函数f：D→Rd，其敏感度为Δf，那么随机算法K（D）=f（D）+Y提供ε-差分隐私保护，其中Y～Lap（Δf/ε）为随机噪声，服从尺度参数为Δf/ε的Laplace分布，其中Lap（Δf/ε）概率密度函数为：

根据公式（3）可得Laplace分布的期望值为0，方差为2λ2.

2）指数机制.

定义4指数机制（Exponential Mechanism）[5].设随机算法K输入为数据集D，输出为一实体对象r∈Range，q（D，r）为可用性估价函数，Δq为函数q（D，r）的敏感度.若算法K满足输出为r的概率与exp（εq（T，r）/2S（q））成比例关系，那么算法K满足服从指数机制的ε-差分隐私.

3）高斯机制（Gauss Mechanism）.与拉普拉斯机制相类似，同样是通过向查询请求结果f（T）中添加服从高斯分布的噪声η，得到f（T）+η来实现ε-差分隐私保护，其概率密度函数为：

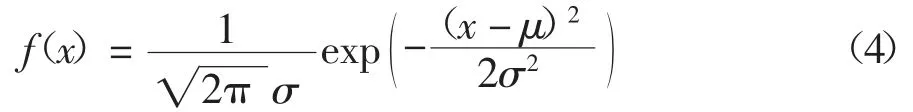
根据公式（4）可得高斯分布的期望值为μ，方差为2λ2，其中λ由全局敏感度和隐私预算ε决定，λ体现了添加噪声的幅度大小以及隐私保护的强度大小，与隐私保护强度成正比.

1.1.4 质量评估指标

1）数据查询准确度.一个具有敏感信息的数据集在经过隐私保护算法处理后，除了要保证敏感信息不外泄，还要保证处理过的数据集中的信息还能够用于研究分析，所以要充分保证数据的可用性.因此，数据查询准确度是衡量隐私保护方法的一个重要指标.本文通过将隐私保护方法得到的数据表与原数据计算重合比，来检验数据查询准确度.

2）隐私保护强度表示在所设计的方法中满足差分隐私的同时，确保隐私信息不被泄露，通常采用差分隐私的定义方法来评价算法是否满足差分隐私的要求.由于差分隐私算法的隐私保护强度目前没有一种定量的测量机制，本文在对隐私保护强度进行评估的时候使用ε以及噪声的方差来近似表示.

3）时间复杂度.本文使用时间复杂度这项指标对所设计的算法进行评价，具体方法是通过计算各个实验的运行时间来进行比较分析.

1.2 经验小波变换

经验小波变换（Empirical Wavelet Transform，EWT）[6]是Gilles提出的一种构建适合处理信号小波族的方法.为清楚起见，只考虑实际信号（它们的频谱相对于频率对称，ω=0），但通过在正负频率中构建不同的滤波器，可以很容易地将以下推理扩展到复杂信号.

把傅里叶频谱划分N份，每个分割的区间定义为Λn=[ωn-1，ωn]，n=1，2，…，N.其中，围绕每个ωn都定义一个过渡段Tn（宽度是2n），这样就需要N+1个边界，除去已知的0和π两个边界，还需要N-1个边界，如图1所示.

考虑到归一化的傅里叶轴具有2π周期性，为了遵守Shannon标准，将信号的频谱变化范围限制在ω∈[0，π]，首先假设傅里叶支持[0，π]被分割成N个连续的段.将ωn表示为每个段之间的界限（其中ω0=0、ωN=π），参见图1.每个段表示为Λn=[ωn-1，ωn]，则很容易看出以每个ωn为中心，在ωn周围定义了一个灰色阴影过渡区域Tn，宽度为2τn.

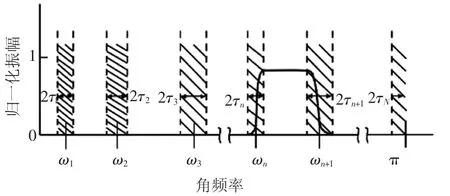
图1 EWT频谱的分割示例Fig.1 Example of EWT spectrum segmentation

EWT算法自适应性的好坏，很大程度上取决于信号频谱中的有用信息能否被包含在相应的过渡区间内.因此，分段数N及其边界点ωn的选取至关重要.分段数N选取的具体流程如图2所示，其中α值取0.3～0.4.确定分段数N后，取M个极大值点中前N个最大值点，即{Mi}Ni=1，找出它们在频谱中的具体位置，取相邻两极大值点所对应频率的中值，记为边界点ω（n=1，2，…，N-1）.经验小波就被定义为每个Λn上的带通滤波器.为此，利用Littlewood-Paley和Meyer的小波构造中使用的思想，对于∀n＞0，分别通过方程（5）和（6）定义经验尺度函数和经验小波.

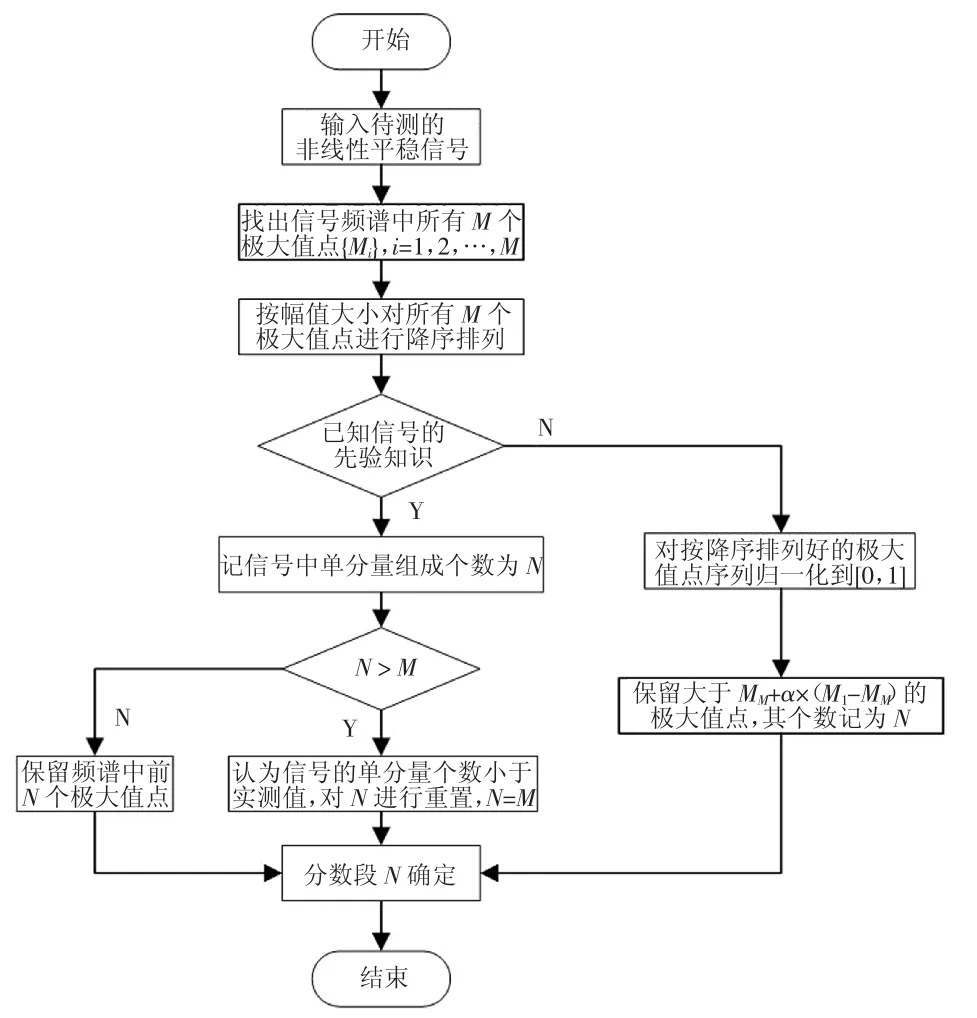
图2 EWT算法中分段数N的计算方法Fig.2 Calculation method of segment number N in EWT algorithm

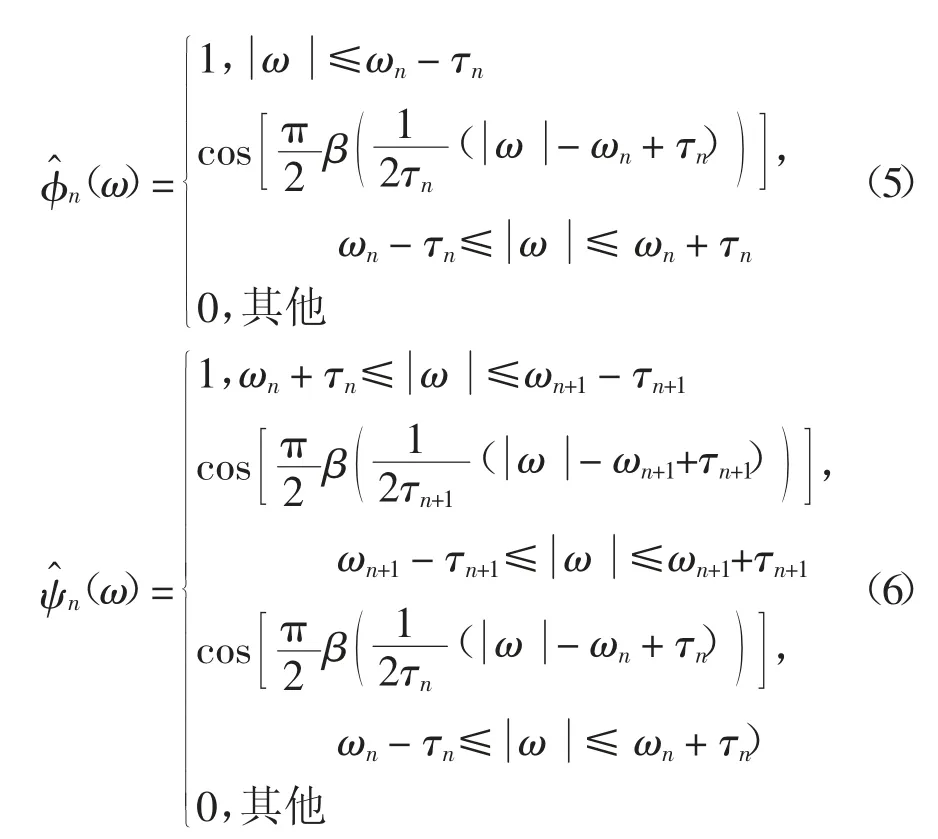
其中：函数β（x）是任意的Ck（[0，1]）函数，许多函数满足这些属性，比如式（5）.

关于τn的选择，有几种选择是可能的.最简单的是选择与τn成比例的ωn∶τn=γωn，其中0＜γ＜1.

EWT的构建.根据经典小波变换理论构建经验小波，细节系数和逼近系数由待测信号与经验小波函数和经验尺度函数分别做内积得到，如式（8）和式（9）所示：

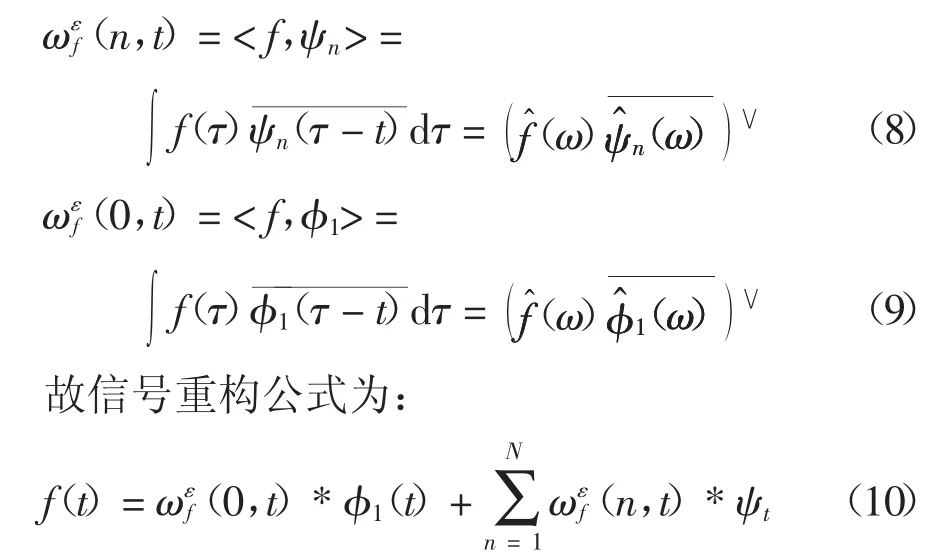
公式（10）中：*表示卷积.根据重构公式，信号f（t）可以由公式（11）得到：

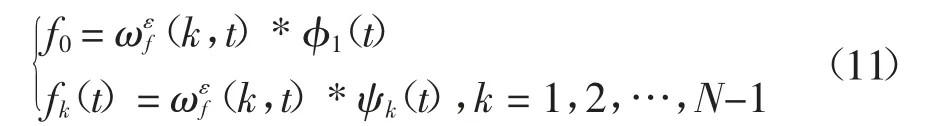
通过经验小波变换将信号分解，获取一系列的调频调幅分量，然后对这些分量处理获取瞬时频率和瞬时幅值.

1.3 致病基因关联分析概述

致病基因相关度分析是本文的研究基础，该技术来源于全基因组关联研究（Genome-wide Association Studies，GWAS），目的是确定群体中哪些常见的单核苷酸多态性（SNP）与给定疾病相关.这是通过采集大量个体，在常见的SNP上对它们进行基因分型，并且对于每个SNP，进行统计测试来检查该SNP是否与所述疾病相关，然后计算每个SNP的相关度并根据相关度进行排序来完成[7].

本文基于差分隐私的GWAS主要集中在对致病基因相关度排序并返回高度相关的SNP这一任务，为了保护私人表型信息（疾病状态）在做致病基因相关度排序以及返回高度相关的SNP算法研究时不被泄露，以隐私保护的方式选择相关度较高的SNP.首先需要使用基于噪声的差分隐私方法进行隐私保护，然后对SNP的疾病相关性进行一系列的计算并评分，最终保证具有隐私保护的同时返回m个相关度较高的SNP，其中m是用户定义的可变参数.

1.4 基于小波变换的差分隐私

为了在满足差分隐私的条件下，提高数据可用性，目前已有实现基于小波变换的差分隐私保护方法[8].该方法需要将数据以及参数λ作为输入，其中参数λ是由不同的噪声机制来确定的[9].图3为基于小波变换的差分隐私实现步骤，其中最主要的有3个步骤.首先要对原数据进行小波变换处理，一般来说，小波变换是一个可逆线性函数，即它将数据集M映射到另一个矩阵C，这样C中的每个数据项都是M中数据项的线性组合，且M也可以从C中无损地重建.C中数据项是由小波变换得到的小波系数，小波系数包含细节系数和近似系数（即高频系数和低频系数）.为了达到更好的降噪效果，经多次实验得出，将低频系数添加差分隐私噪声会得到更好的效果，算法的准确度会比较高.本节中C1为小波的低频系数，C2为小波的高频系数.

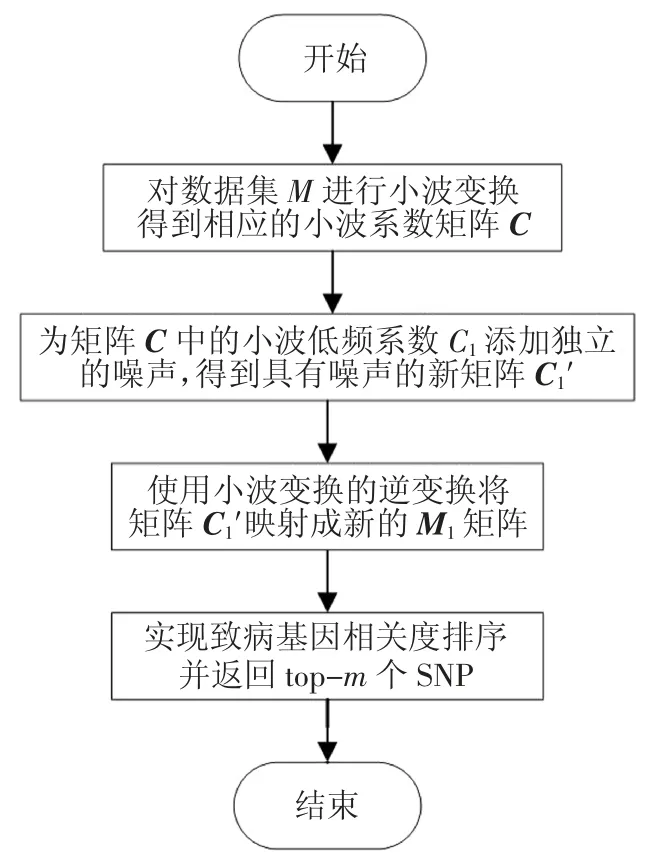
图3 基于小波变换的差分隐私实现步骤Fig.3 Differential privacy implementation steps based on wavelet transform

其次，在小波变换之后，为了保证实现差分隐私保护，需要为C1中的小波低频系数添加独立的噪声（拉普拉斯噪声、指数分布噪声或者是高斯噪声），这一步将得到具有噪声系数的新矩阵C1′.

最后，将矩阵C1′使用小波变换的逆变换映射成具有差分隐私保护效用的矩阵M1，并将该矩阵作为经过基于小波变换的差分隐私算法处理过的结果输出返回.

1.5 基因关联分析中的其他隐私保护技术

文献[10]采用同态加密和Intel软件保护扩展技术实现全基因组关联分析中的隐私保护.文献[11]采用博弈论的方法实现大规模基因数据有效、定量的隐私保护.文献[12]提出一种分析全基因组上位性的新方法，该方法采用二阶段框架的上位性分析方法，它包含特征过滤阶段以及上位性组合优化阶段，在上位性组合优化阶段采用贪婪算法启发式地搜索组合空间.

2 基于EWT的差分隐私

2.1 基于EWT的差分隐私的实现

本文是在满足差分隐私保护的前提下，对数据添加的噪声量进行一个降噪处理，最终得到较高可用性的数据集.为了实现以上方法，本文提出将EWT变换应用到差分隐私的噪声处理中.该方法的具体步骤如图4所示，首先使用差分隐私对数据进行处理，得到已满足差分隐私的数据集，然后对该数据集进行相关EWT的处理.对于EWT的处理，首先，对数据集进行EWT分解，得到N个分段，并根据N个分段中信号的峭度值进行筛选并重构信号，得到最终降噪后的数据集.实验最后使用该数据集来实现致病基因相关度排序，并对实验的隐私保护强度以及算法性能进行评估.

图4中根据峭度值筛选算法的具体步骤如下：

1）计算信号x（t）经EWT分解后各分量的峭度值μn：

式中：N为采样点数；cnk为EWT分解之后的分量.

2）根据μn得到各分量峭度值的集合μ：

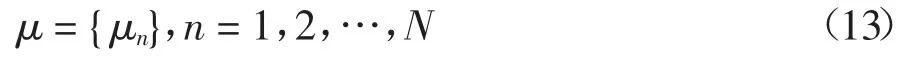
3）定义信号的调频调幅分量的峭度因子Zn：

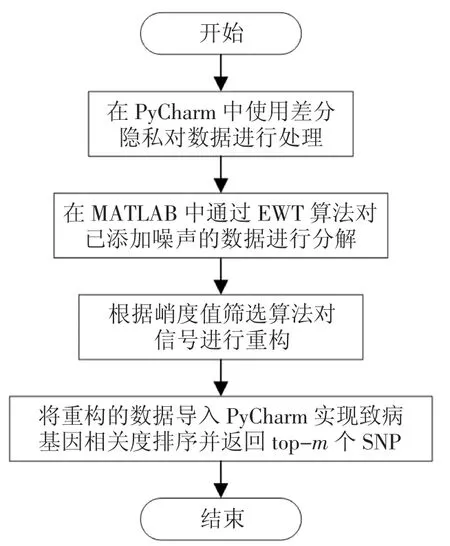
图4 基于EWT变换的差分隐私实现步骤Fig.4 Differential privacy implementation steps based on EWT transform

4）根据峭度因子选择峭度分量.按照峭度因子从大到小的顺序将所有调频调幅分量进行重新排序，得到新的序列为排序后的峭度因子.

5）求出相邻两个调频调幅分量的峭度因子之差，之后找出最大差值dn.

2.2 EWT降噪实例

根据2.1节描述的基于EWT的差分隐私实现方式，对差分隐私的3种噪声机制进行实验对比，得出结果如图5所示.由图5可以看出，基于Gauss噪声机制的差分隐私准确度较高，因此本文后续的差分隐私保护实验均以Gauss噪声机制为例.

图5 基于不同噪声机制的差分隐私算法准确度Fig.5 Accuracy of differential privacy algorithm based on different noise mechanisms

在本文致病基因相关度研究实验中，使用差分隐私添加Gauss噪声进行EWT降噪.首先添加Gauss噪声，然后采用EWT算法进行滤波仿真，最后将重构的数据提取后进行致病基因相关度排序实验并返回相关度最高的m个SNP.

在使用EWT算法进行滤波仿真时，首先对包含Gauss噪声的数据做傅里叶变换，提取傅里叶分段的边界，根据对含噪声的信号进行有效估计，确定滤波器组的边界频率.所得频谱分割结果如图6所示.

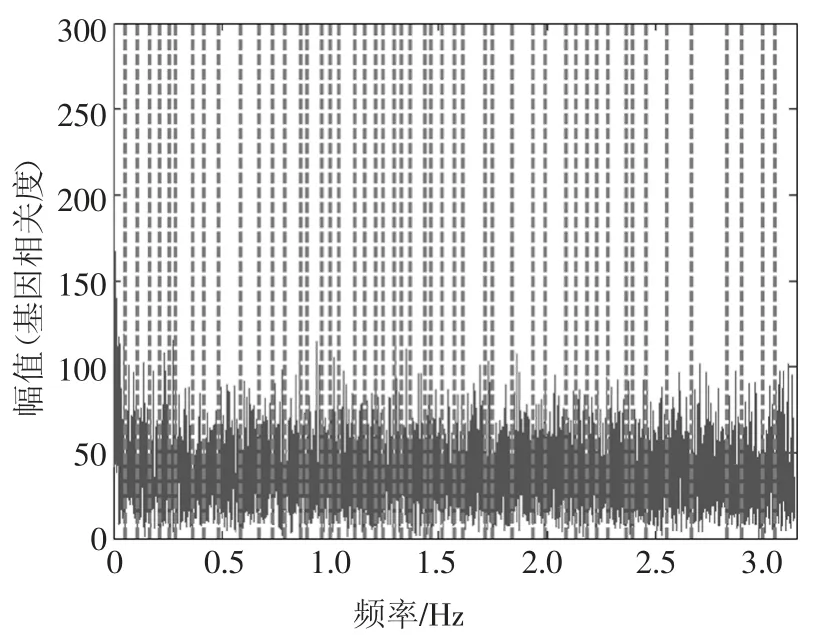
图6 EWT频谱分割Fig.6 EWT spectrum segmentation

提取边界之后，通过镜像来扩展信号以处理边界，并建立相应的滤波器库，通过过滤信号来提取每个子带.划分的频带共有50组，因此仿真信号的经验小波变换分解（EWT）的信号共有50组，用F1～F50表示.图7为分解的50组EWT分量中的7组分量信号，从上到下依次表示为F1～F6.

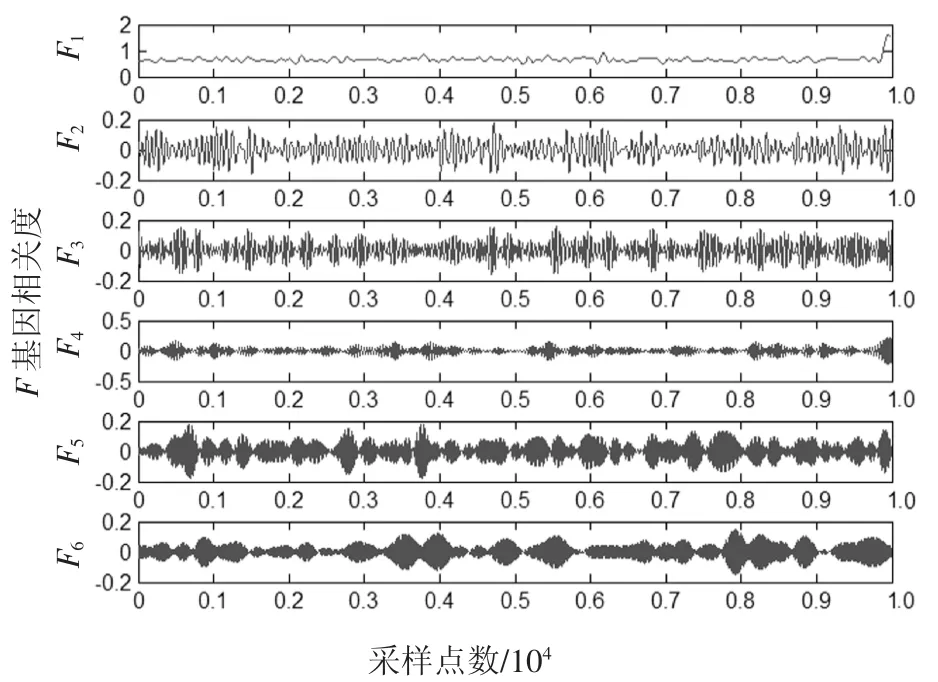
图7 经EWT算法分解后的分量示例Fig.7 Example of component decomposed by EWT algorithm

对于EWT分解得到的分量，根据2.1节中的筛选算法计算出峭度因子，并对其进行排序，排序前后的对比如图8所示.根据进一步计算可得，排序后两个峭度因子之差的最大值位于F1和F23之间，最大差值为0.976 6，依据3.1节中根据峭度值筛选重构信号的算法可以得出，F1以及F24～F50为噪声成分，而F2和F23之间包含主要的峭度成分，作为信号x（t）的有效特征分量.接下来，对F2～F23个分量进行重构，形成重构信号.图9为原信号、添加Gauss噪声后的信号以及重构信号的结果对比，纵轴相关度参数为致病基因相关度排序算法中计算疾病与基因相关度的实验数据.从图9的对比结果可以看出，添加Gauss噪声后的信号分布较为杂乱，而重构之后的信号相关度系数均匀分布在-0.15～0.15内，没有较大或者较小的信号.

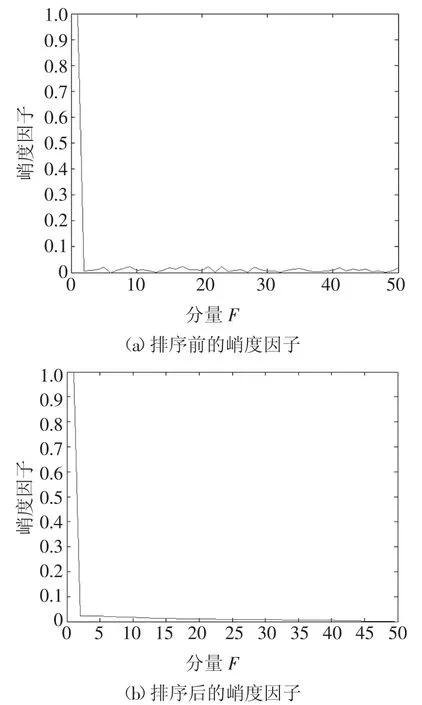
图8 排序前后的峭度因子Fig.8 Kurtosis factor before and after sorting

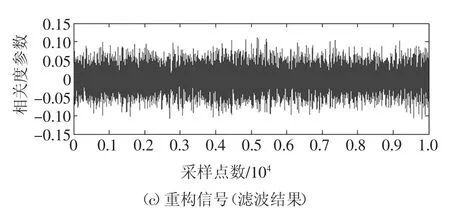
图9 采用EWT算法对Gauss噪声的降噪结果对比Fig.9 Comparison of noise reduction results of Gauss noise using EWT algorithm

3 实验与结果分析

本节对ε-差分隐私、基于EWT变换以及基于小波变换的3种差分隐私的保护效果进行实验对比分析.具体实验中的差分隐私分别使用拉普拉斯机制、指数机制以及高斯机制3种实现机制，并设置不同的隐私参数ε，以及返回前m个与疾病具有高相关度的SNP来对实验结果的影响进行测试.

3.1 数据集及实验环境

实验平台为Intel（R）Core（TM）i7-6700HQ 2.60 GHz处理器，8 G内存，操作系统为Windows10，编程环境为MATLAB R2014a以及Pycharm 2016.3（64）.

主要的测试数据来自某一类风湿性关节炎（RA）数据集NARAC-1，这组数据由Plink工具生成，该数据集及其生成代码（基于Plink工具）可在线获取.它包含2个种群，对于每一组，首先使用plink为10 000个SNP选择MAF（Minor Allele Frequency），在某些条件下，最小等位基因频率可以使用统计方法来准确和稳健地解析在已知只有MAF的DNA样本混合物中存在已知基因型的个体，每个SNP从[0.05，0.5]中随机均匀选取.然后，从每个人群中生成了5 000人，有2 500个病例和2 500个对照病例.结果为每个样本有10 000个SNP，9 900个无效，100个引起疾病（奇数比率1.1）.然后将这2个群体组合起来生成模拟数据集，该模拟数据集是一个1×10 000的矩阵.

3.2 实验步骤

本文中实验的主要步骤如图10所示.分别使用基本的ε-差分隐私（DP）、基于小波变换（WT-DP）以及基于EWT变换（EWT-DP）这3种差分隐私算法来进行实验，并对这3种算法的实验结果进行对比分析.在这3种算法的对比实验中，选择使用表现较好的Gauss机制来实现基本的差分隐私.另外，对基于EWT变换的差分隐私噪声实现机制进行评估实验，该实验中分别使用Laplace、Exponential以及Gauss机制来实现基本的差分隐私.

图10 实验步骤Fig.10 Experimental procedure

3.3 隐私保护强度评估

本节对各种差分隐私算法的保护强度进行比较评估.由于差分隐私算法的隐私保护强度目前没有一种定量的测量机制，但是噪声参数λ体现了添加噪声的幅度大小以及隐私保护强度的大小.因此，本文在对隐私保护强度进行评估的时候，通过计算噪声参数λ以及噪声分布的方差来近似表示.

图11的实验结果是对ε-差分隐私（DP）、基于小波变换（WT-DP）以及基于EWT变换（EWT-DP）的差分隐私算法的保护强度的比较，这3种方法中使用到的差分隐私均使用Gauss噪声机制来实现.本文中隐私保护强度是根据噪声的方差来进行计算的.图11结果表明，3种方法中ε-差分隐私算法的隐私保护强度相对较高，基于EWT变换的差分隐私算法的隐私保护强度相对较低，但差距并不大，这表明使用EWT变换可以保证一定量的隐私保护效用.

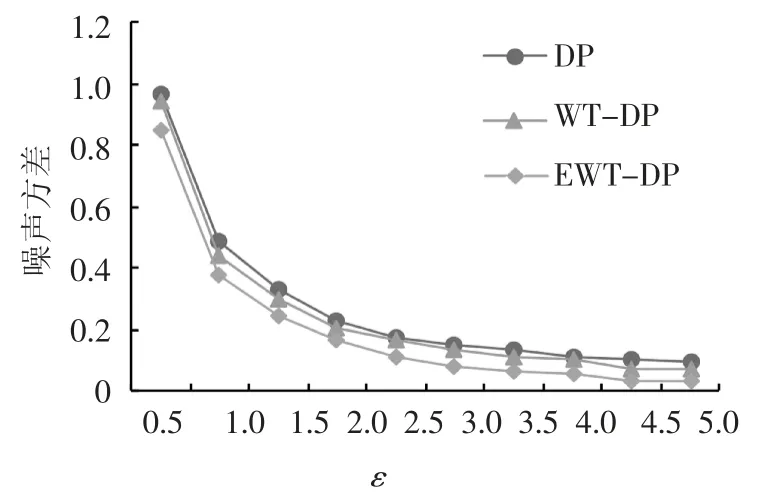
图11 3种差分隐私算法的隐私保护强度对比Fig.11 Comparison of privacy protection strength of three differential privacy algorithms

图12的实验结果是基于EWT变换的3种差分隐私噪声实现机制的隐私保护强度的比较，实验中分别使用Laplace、Exponential以及Gauss机制来实现基本的差分隐私，横坐标为ε的值.实验结果表明，差分隐私的保护强度与ε负相关，ε的值越大，差分隐私所添加的噪声越小，噪声方差也越小，因此差分隐私的保护强度也越小.

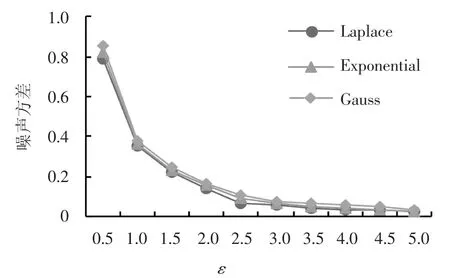
图12 基于EWT变换的差分隐私实现机制的隐私保护强度对比Fig.12 Comparison of privacy protection strength of differential privacy implementation mechanism based on EWT transform

3.4 算法时间复杂度

基于EWT变换的差分隐私算法时间复杂度主要由以下几步决定：1）对数据表进行差分隐私加噪处理，将数据表映射成便于计算的序列M；2）对序列M进行EWT变换分解得到一系列的EWT分量；3）计算峭度值并根据峭度值来筛选重构信号；4）对信号进行重构，并提取降噪数据；5）使用降噪数据进行致病基因相关度排序算法，返回m个与疾病高度相关的SNP.总的时间复杂度近似为以上5个主要步骤的时间复杂度相加.

由于本文提出的基于EWT变换的差分隐私保护算法包括以上所列5个步骤，而ε-差分隐私（DP）理论上只包括步骤1）、步骤5）；而基于小波变换（WT-DP）的差分隐私算法理论上虽然包括步骤1）～步骤5），但是与本文所提的变换方法和降噪方法不同；所以，在运行时间上存在一定差异.

依据3.2节中的实验步骤进行实验并计算算法时间复杂度，对3种算法的运行时间计算20次并取平均值作为实验结果.

图13中的3种差分隐私算法均使用Gauss机制实现，可以看出基于EWT变换的差分隐私相较于其他2种差分隐私算法来说所花费的运行时间较长，性能比较低，这是因为EWT变换的过程相对于其他2种方法所花费的时间比较长.

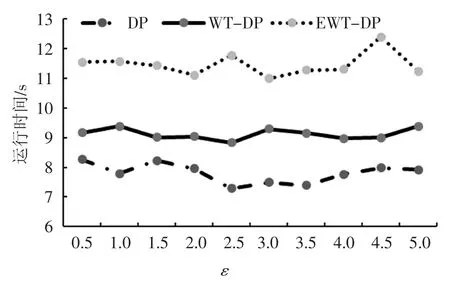
图13 3种差分隐私算法的运行时间对比Fig.13 Comparison of run time of three differential privacy algorithms

图14的结果是基于EWT变换的3种差分隐私噪声实现机制的运行时间对比，可以看出基于Gauss机制的运行时间最短，性能最佳.

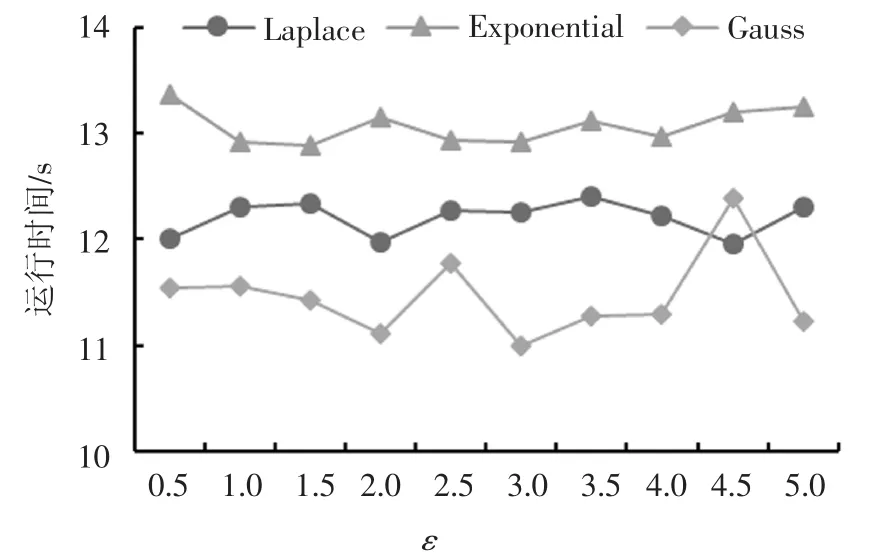
图14 基于EWT变换的差分隐私实现机制的运行时间对比Fig.14 Comparison of run time of differential privacy implementation mechanism based on EWT transform

3.5 致病基因相关度排序准确度评估

本文通过计算致病基因相关度排序的准确度来对经差分隐私处理过的数据的数据质量进行评估，具体做法是计算每次实验返回结果与真实结果重合的百分比，作为算法准确度的度量.

依据3.2节中的实验步骤进行实验并计算算法时间复杂度，得出结果分别如图15、图16所示，这些结果均在20次迭代中取平均值.

图15中的3种差分隐私算法均使用Gauss机制实现，可以看出，经EWT变换后的差分隐私所得的致病基因相关度排序的准确度相对于其他2种方法比较高，也就是说使用该种方法处理数据的数据质量比较好.

图16中基于EWT变换的3种差分隐私噪声实现机制中Gauss机制的准确度较高.

用户可以根据其实际需求，采用本文所提方法设置相应的噪声注入量和过滤量，实现合理的隐私保护效果.

本文所提方法基于经验小波变换，假设需要隐私保护的基因数据规模为N，经验小波变换的时间复杂度是O（N log（N））[6]，整数全同态加密算法时间复杂度是O（N3）[13]，本文所提方法与同态加密隐私保护技术相比，具有较低的计算时间复杂度.

图15 3种差分隐私算法的准确度对比Fig.15 Comparison of accuracy of three differential privacy algorithms

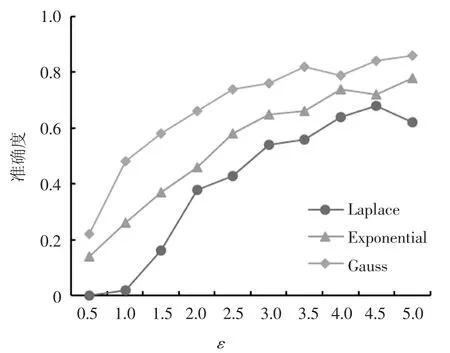
图16 基于EWT变换的差分隐私实现机制的准确度对比Fig.16 Comparison of accuracy of differential privacy implementation mechanism based on EWT transform

4 结论

针对在致病基因相关度排序实验中数据因添加差分隐私噪声而导致的数据可用性较低这一问题，本文提出了一种基于EWT变换的差分隐私保护方法，设计了实现步骤并通过实验验证了该方法的可行性和正确性.实验结果表明，该方法在保证了差分隐私保护强度的条件下，能够较为显著地提高致病基因相关度排序数据的可用性和准确度，实现了数据隐私保护强度与可用性的有效权衡.下一步将继续研究如何在保证算法准确度的情况下降低隐私保护算法的时间复杂度.