一种基于改进辛几何模态分解的复合故障诊断方法

杨宇，程健，彭晓燕，潘海洋，程军圣

（湖南大学机械与运载工程学院，湖南长沙410082）

齿轮、滚动轴承等零部件作为机械设备的核心元素，其状态好坏直接关系到整个机械设备的运转性能.当前，针对这种现象学者们已经开展研究，并取得了一定的成果.但是大多学者只针对某单一故障进行研究，却忽视了复合故障存在的可能性.当机械设备出现复合故障时，多种故障信号相互耦合以及在强噪声的干扰下使得故障类型分析难度加大[1].因此，需要采用合适的信号分析方法提取出有效的故障信息进行分析.

经验模态分解（Empirical Mode Decomposition，EMD）[2-3]方法作为一种典型的信号分析方法，可以将待分析信号分解为若干个有意义的内禀模态函数（Intrinsic Mode Function，IMF）之和.IMF分量的频率受采样频率的影响，同时也随着原始信号的变化而变化，通过迭代和极值点包络可以有效地从待诊断信号中提取出含有故障信息的分量信号.因此EMD方法是一种自适应的信号分析方法，适合用于处理非平稳信号.局部特征尺度分解（Local Characteristic-scale Decomposition，LCD）[4-5]方法是近几年提出的一种新方法，该方法借鉴EMD的思想通过设置基线信号将信号分解成多个内禀尺度分量（Intrinsic Scale Component，ISC）之和.与EMD方法相比，该方法运算速度大大提高，信号处理效率得到明显提升，适用于在线监测.虽然EMD和LCD在处理非平稳信号以及运算效率方面具有一定的优势，但它们同样也存在着许多难以克服的缺点，如端点效应和模态混叠等.对此，相关学者已经做出大量研究工作，并提出相应的改进方法，抑制了端点效应、模态混叠等现象，但是又带来了新的不足.例如提出的集合模态分解（Ensemble Empirical Mode Decomposition，EEMD）方法一定程度上抑制了模态混叠现象，但增加了计算量，同时无法完全中和添加的白噪声，使EEMD不具有完备性.

近年来，随着辛几何谱分析（Symplectic Geometry Spectrum Analysis，SGSA）[6-8]方法的提出，许多学者对其做了大量研究.该方法是一种基于辛几何的信号分析方法，其核心是通过辛几何相似变换在不改变原时间序列本质特征的基础上获得相应的辛几何分量.SGSA方法具有较强的抗噪能力，在处理非平稳故障信号中有着较好的效果，但它同时也存在着自身的不足，主要有以下两点：第一，无法自适应地选择嵌入维数构造轨迹矩阵；第二，当进行辛几何重构时，该方法利用周期、频率等相似性来重构出最终的辛几何分量，并需要人为设置终止条件.这些不足会导致最终的分析结果具有不确定性，严重影响辛几何谱分析方法的推广.针对第一点不足，Pan等[9]将辛几何模态分解（Symplectic Geometry Mode Decomposition，SGMD）方法应用于故障诊断，采用功率谱密度（Power Spectral Density，PSD）方法自适应地确定嵌入维数，从而消除了人为设置嵌入维数给结果带来的不确定性.但其辛几何分量的构造依然采用频率和相关系数相似度，同时也需要人为地设置迭代终止条件.该缺陷将导致SGMD方法所得到的最终分析结果依然存在着一定的不确定性.针对SGMD方法的这一缺陷，本文提出了一种改进的辛几何模态分解（Improved Symplectic Geometry Mode Decomposition，ISGMD）方法，该方法首先对待分析的时间序列信号进行相空间变换，获得轨迹矩阵；其次将轨迹矩阵进行辛几何相似变换求出特征值，所求特征值对应的特征向量经过重构得到具有原始信号完整结构信息的辛几何分量矩阵；然后对辛几何分量矩阵做对角平均化得到一系列的初始辛几何分量；最后采用层次聚类方法对初始辛几何分量进行自适应重组，进而得到最终的聚类辛几何分量（Cluster Symplectic Geometry Component，CSGC）.

本文利用层次聚类（Hierarchical Cluster）方法[10-11]不需要设置聚类的阈值就可以得到较为准确的聚类结果这一优点，将层次聚类方法引入到SGMD方法中，其目的是为了实现分量自适应地重组，提高分析结果的准确性.基于ISGMD是一种非平稳信号处理方法，同时可以将复合故障信号分解成若干个含有不同频率信息的辛几何分量的特点，本文的ISGMD方法可用于旋转机械复合故障诊断.

1 改进的辛几何模态分解方法

1.1 相空间重构

令始时间序列为x={x1，x2，…，xn}，n为时间序列长度，对时间序列进行相空间重构得X：

式中：k为嵌入维数；τ为延时时间；m=n-（k-1）τ.选择合适的嵌入维数k和延时时间τ，可以得到相应的重构矩阵X.嵌入维数k过大会增加计算量，同时加大噪声的影响；嵌入维数k过小会使数据重叠，导致重构矩阵无意义[12].功率谱密度（PSD）计算简单（只需知道原始时间序列峰值对应的频率），并且能够自适应确定嵌入维数.因此，采用功率谱密度（PSD）方法确定嵌入维数[12]，并定义PSD中最高峰的频率为Fmax，Fs为采样频率.当归一化频率Fmax/Fs小于0.001时，k=N/3，否则k=1.2×（Fs/Fmax）.根据重构矩阵可以构造Hamilton矩阵W为：

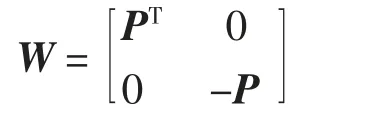
其中P=XTX.

1.2 辛几何相似变换

正交辛矩阵Q为：

因为Q矩阵是正交辛矩阵，因此矩阵Q有着辛矩阵的性质.在辛变换的过程中，保留了Hamilton矩阵的结构特征，所以变换后的矩阵依然是Hamilton矩阵.式（2）中H是上三角矩阵，其中Hk×k=（hij）k×k，当i≥j+1时，hij=0.通过对矩阵W进行变换，就可以计算出上三角矩阵H的特征值λ（H），由Hamilton矩阵的性质可得λ（W）=λ（H），，由矩阵的性质可知：特征值的数量为k个，所以按降序的顺序排列矩阵P的特征值为σ1，σ2，…，σk，设Ai（i=1，2，…，k）为矩阵P特征值σi所对应的特征向量，令，则可以获得一个新的重构矩阵，进而重构的相空间矩阵可以表示为：

1.3 对角平均

采用对角平均将重构矩阵Zi（1≤i≤k）转化为一个长度为n的辛几何分量，经过对角平均后，获得可以生成k组长度为n的辛几何分量，具体过程如下：记Zm×k=（zij）m×k，1≤i≤m，1≤j≤k，令k*=min（m，k），m*=max（m，k），n=m+（k-1）τ.当m＜k时，否则

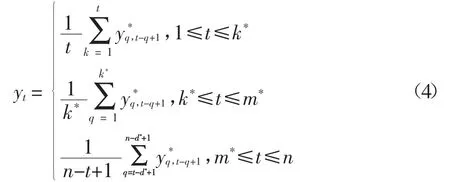
由式（4）可以逐一确定y1，y2，…，yn，所以就得到了与重构矩阵Zi相对应的一组一维长度为n的序列Yi.按照上述步骤对k个重组矩阵Zi进行对角平均，即可获得k组长度为n的序列Yi，对应着原始时间序列分解出的k个不同频带的独立分量.将k组序列Yi构成新的矩阵Y，进而对角平均所得到的初始辛几何分量可以表示为：

1.4 分量重组

采用层次聚类方法对初始辛几何分量Y=Y1+Y2+…+Yk进行分析并重组.将每个一维分量Yi看成一个聚类中心ti=（Yi），构成Y的一个聚类集合T=（t1，t2，…，tk）.然后计算T中每对聚类（ti，tj）的相似度.选取相似度最大的聚类对（ti，tj），将其合并成新的聚类td=ti∪tj，同时合并两者所对应的Yi和Yj，将初始辛几何分量重新整理为Y=Y1+Y2+…+Yk-1，并生成新的聚类集合T=（t1，t2，…，tk-1）.循环上述步骤，当聚类分组数为p时停止，此时生成p组最终的聚类辛几何分量，并可表示为：

2 仿真信号分析

为了检验所提方法的有效性，采用轴承和齿轮复合故障仿真信号进行验证.其中轴承系统的固有频率为fn=3 000 Hz，轴承故障特征频率为fg=100 Hz，故障齿轮所在轴的转频为fr=40 Hz，采样频率为8 192 Hz，采样点数为4 096，设轴承和齿轮仿真信号模型分别为：

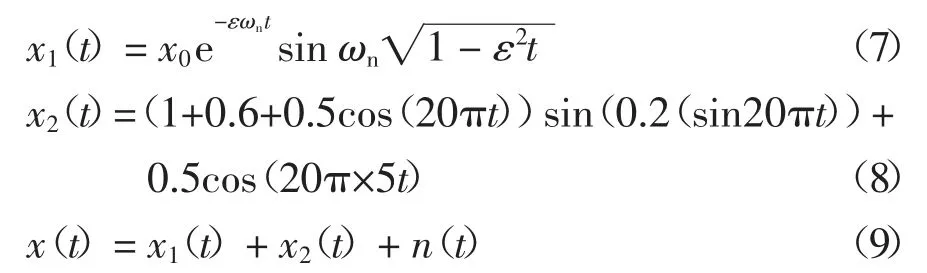
式中：位移常数x0=5；阻尼系数ε=0.1；ωn=2πfn；x（t）为复合仿真信号；n（t）为信噪比，其值为10 dB的高斯白噪声.仿真信号时域波形图如图1所示，图2和图3分别为复合仿真信号的频谱图.

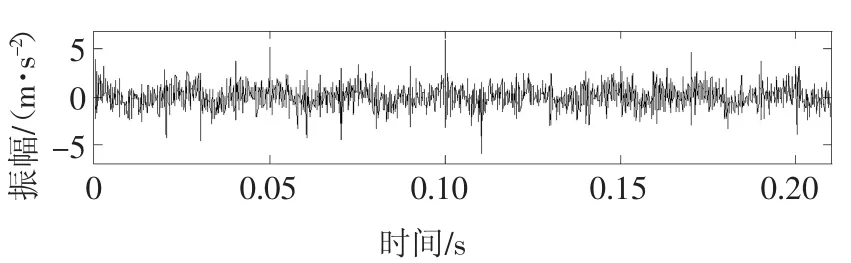
图1 复合故障仿真信号波形图Fig.1 The waveform of composite fault simulation signal

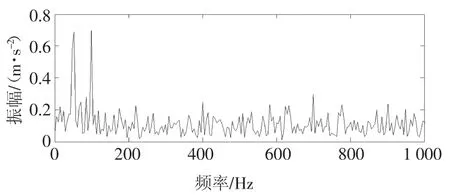
图2 复合故障仿真信号频谱图Fig.2 The spectrum diagram of composite fault simulation signal

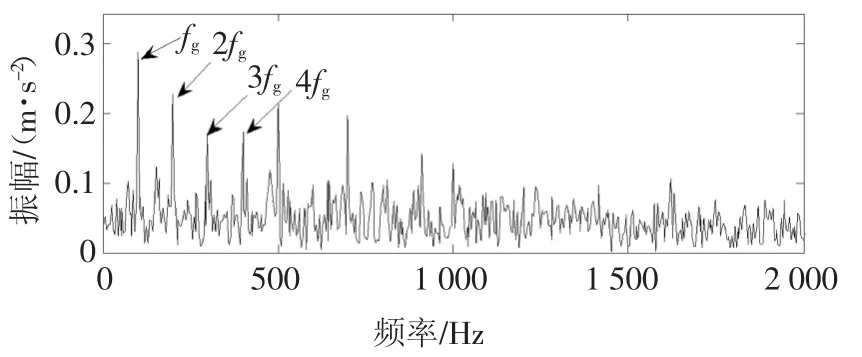
图3 复合故障仿真信号包络谱图Fig.3 The envelope spectrum of composite fault simulation signal

图2和图3中，可以明显看出轴承故障特征频率，但是齿轮故障的特征信息（即故障齿轮所对应的啮合频率及其边频带）被完全掩盖.因此，需要采用信号分析方法对复合故障信号进行分解，以得到具有各类故障信息的分量信号.同时，为了说明ISGMD的分析效果，拟与EMD、LCD和SGMD方法进行对比分析，4种方法的分解结果分别如图4～图7所示.

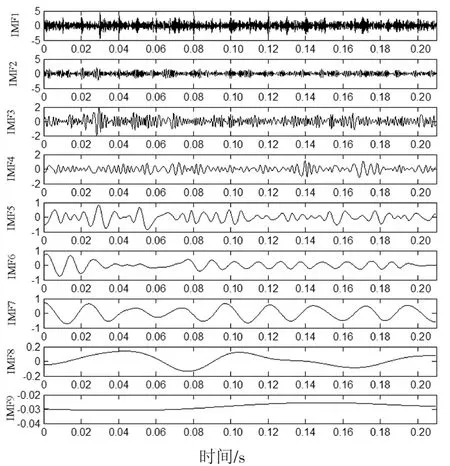
图4 仿真信号EMD分解所得的分量Fig.4 The components obtained by EMD decomposition of simulation signal

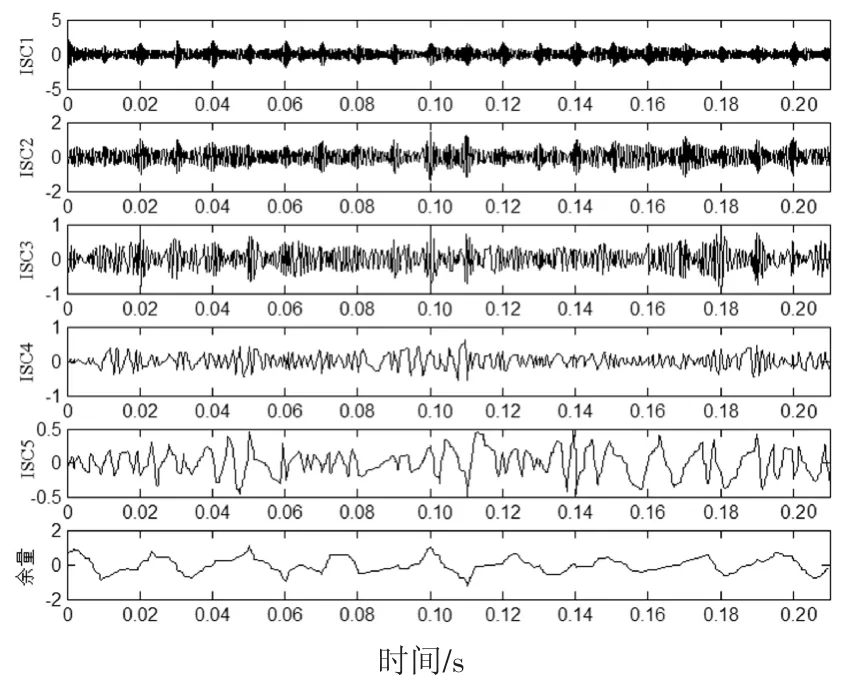
图5 仿真信号LCD分解所得的分量Fig.5 The components obtained by LCD decomposition of simulation signal

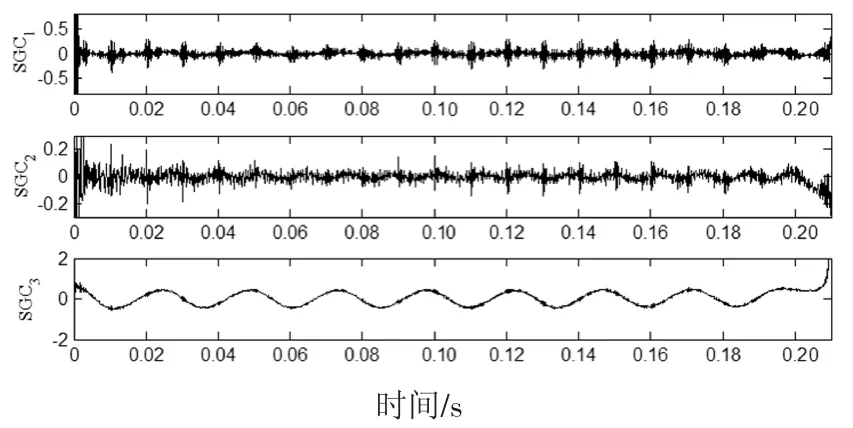
图6 仿真信号SGMD分解所得的分量Fig.6 The components obtained by SGMD decomposition of simulation signal

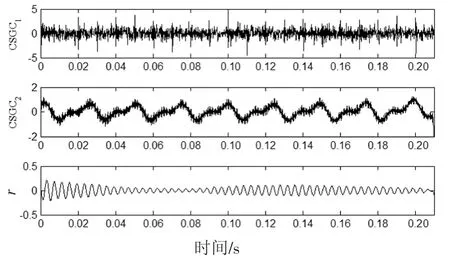
图7 仿真信号ISGMD分解所得的分量Fig.7 The components obtained by ISGMD decomposition of simulation signal

图4～图7为4种方法分解所得到的分量，接着对4种方法的分量信号进行包络谱分析.首先将分量与原信号进行相关性分析，取4种方法分解所得的相关系数较大的前若干个分量分别进行包络谱分析，结合齿轮和滚动轴承的故障特征频率，最终确定取EMD、LCD方法分解所得的前4个分量和SGMD、ISGMD方法分解所得的前2个分量进行包络分析.以EMD分解所得IMF分量为例，将其与复合仿真信号进行相关性分析，所得的相关系数如图8所示.取相关系数较大的前4个分量进行包络分析，结果如图9所示.相似地，LCD、SGMD和ISGMD方法分解的分量包络图分别如图10～图12所示.

从图9～图12可以看出，图9、图10和图11中有明显的轴承故障特征频率及其倍频，但没有提取出齿轮故障特征频率；图12中同时提取出了齿轮和轴承的故障特征频率及其倍频.对比可知，ISGMD方法能够更好地识别出复合仿真故障信号的故障类型.

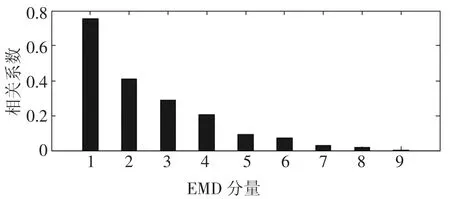
图8 EMD分量与原信号的相关系数Fig.8 The correlation coefficients between EMD components and original signal

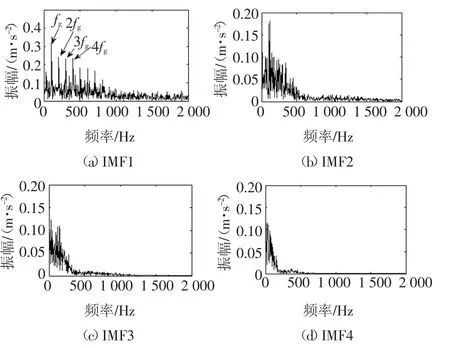
图9 仿真信号EMD分解分量的包络谱图Fig.9 The envelope spectrum of EMD decomposition components of simulation signal

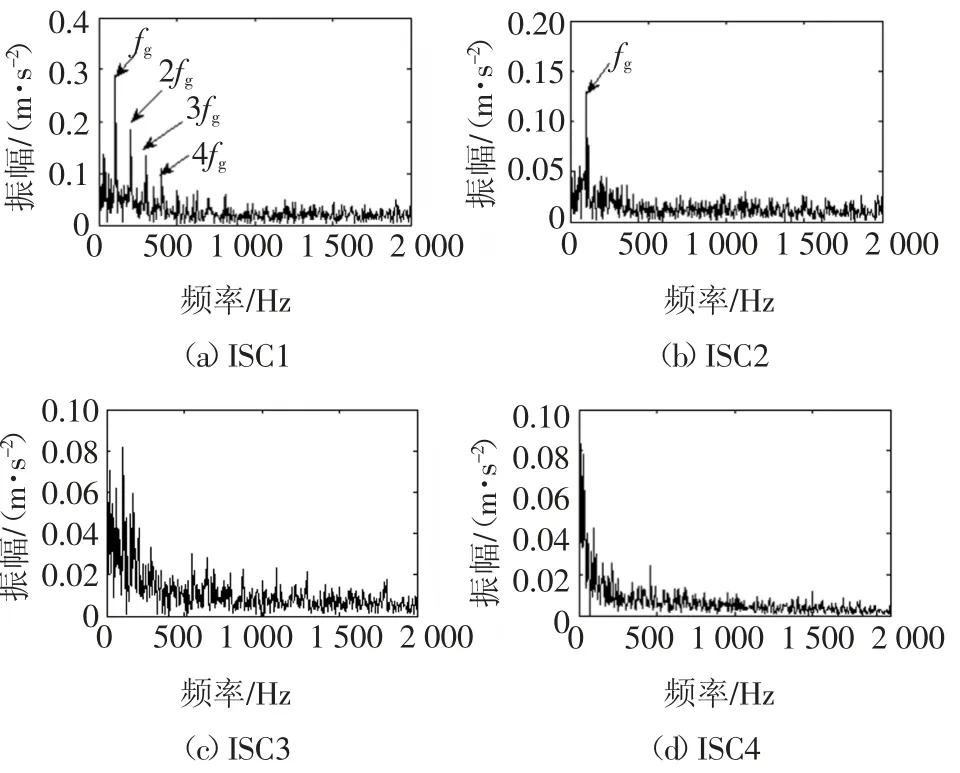
图10 仿真信号LCD分解分量的包络谱图Fig.10 The envelope spectrum of LCD decomposition components of simulation signal

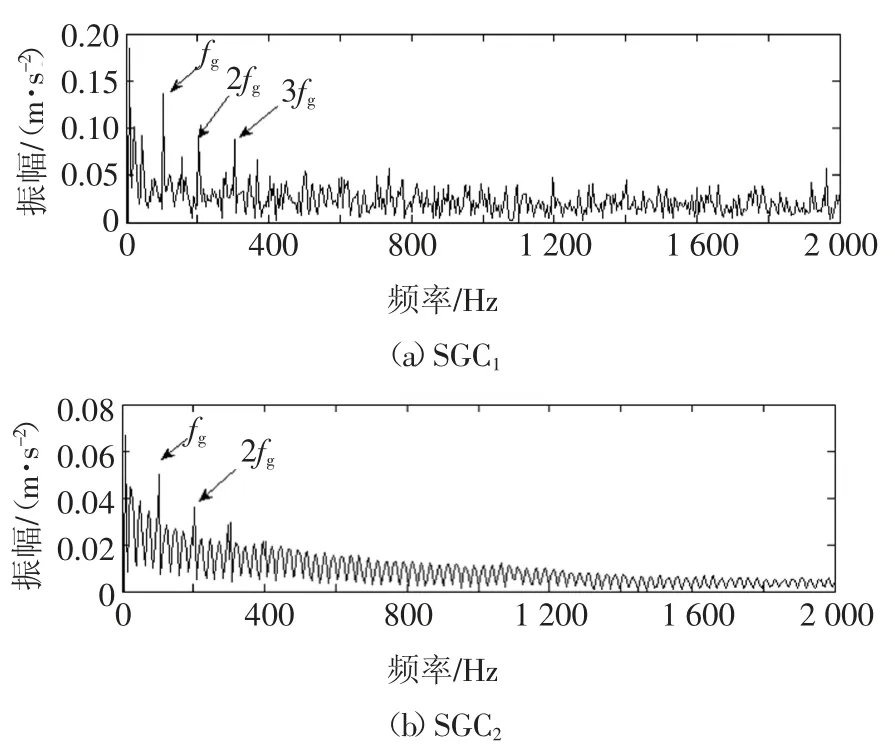
图11 仿真信号SGMD分解分量的包络谱图Fig.11 The envelope spectrum of SGMD decomposition components of simulation signal

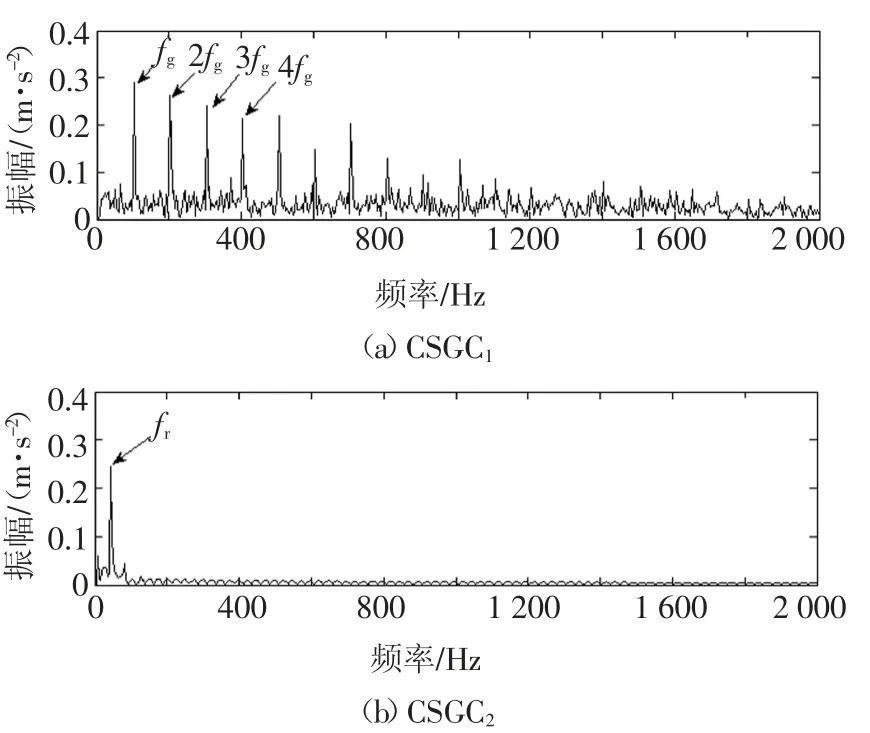
图12 仿真信号ISGMD分解分量的包络谱图Fig.12 The envelope spectrum of ISGMD decomposition components of simulation signal

3 实例分析

为了验证ISGMD在实际故障诊断中的有效性，运用ISGMD对实际的复合故障信号进行故障诊断分析.实验台采用6307深沟球轴承，齿轮箱主动轮和从动轮齿数均为37，转速为900 r/min，采样频率为8 192 Hz，轴承外圈故障特征频率为f0=31 Hz，故障齿轮所在轴的转频为fr=15 Hz.使用激光切割技术在齿轮根部切割出槽宽为0.15 mm，槽深为0.10 mm的槽，并在轴承外圈开槽，槽宽为0.15 mm，槽深为0.13 mm.图13为复合故障信号，图14为实际复合故障信号的包络谱图.

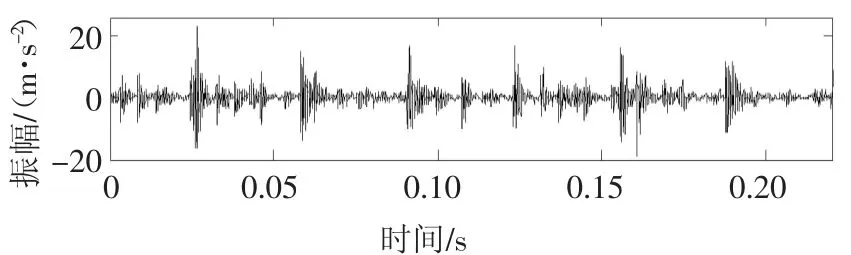
图13 复合故障信号波形图Fig.13 The waveform of composite fault signal

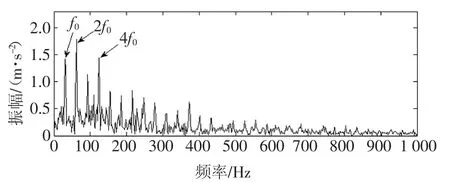
图14 复合故障信号包络谱图Fig.14 The envelope spectrum of composite fault signal

图14只提取出轴承故障特征频率及其倍频.为了提取出完整的故障特征信息，需采用合适的信号分析方法对复合故障信号进行分解.同样地，为了说明ISGMD方法的分析效果，继续与EMD、LCD和SGMD方法进行对比分析，4种方法的分解结果如图15～图18所示.

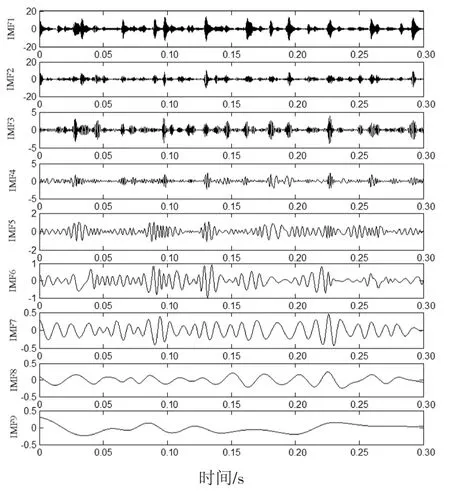
图15 实验信号EMD分解所得的分量Fig.15 The components obtained by EMD decomposition of the experimental signal

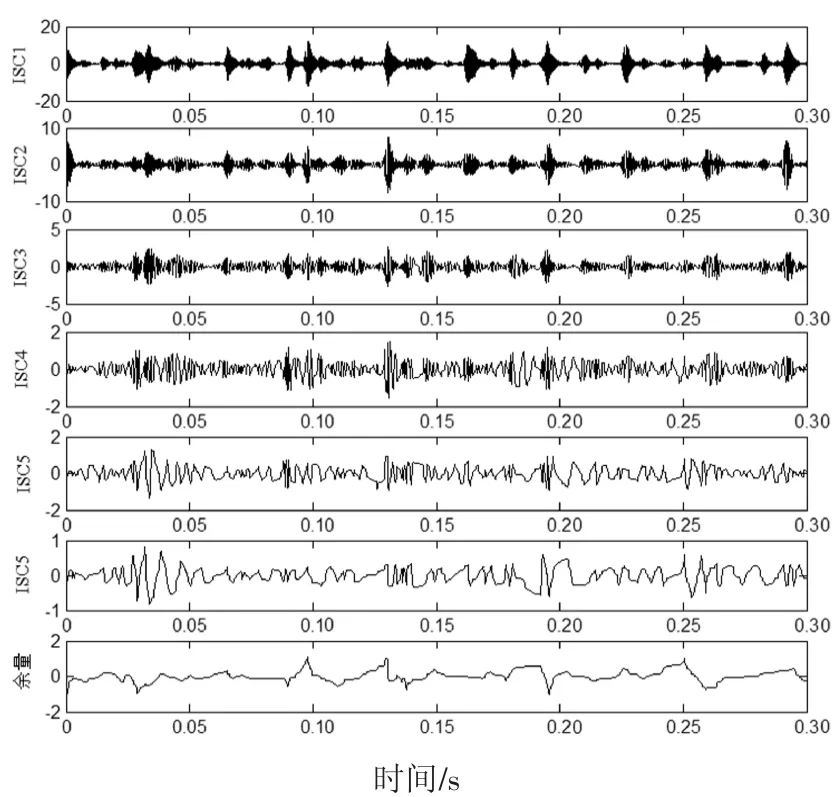
图16 实验信号LCD分解所得的分量Fig.16 The components obtained by LCD decomposition of the experimental signal

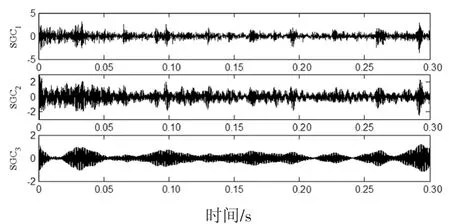
图17 实验信号SGMD分解得的分量Fig.17 The components obtained by SGMD decomposition of the experimental signal

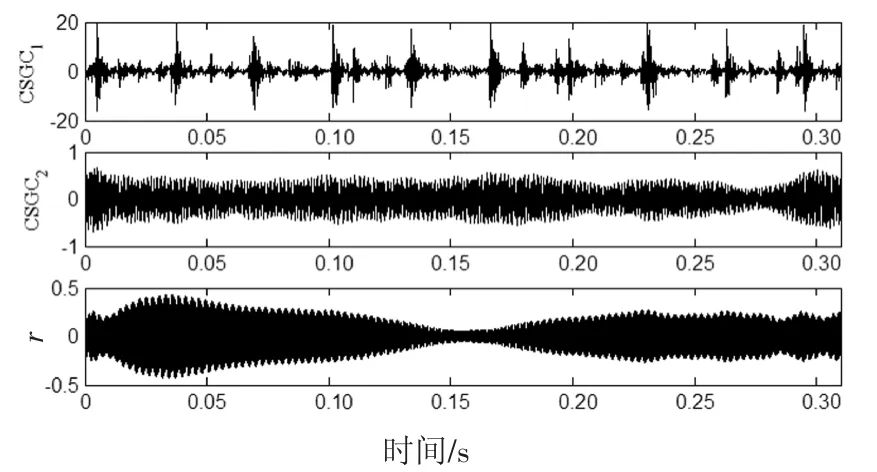
图18 实验信号ISGMD分解得的分量Fig.18 The components obtained by ISGMD decomposition of the experimental signal

图15～图18为4种方法分解所得到的分量.同仿真信号分析相似，接着对EMD、LCD与原信号相关性大的前4个分量和SGMD、ISGMD与原信号相关性大的前2个分量进行包络谱分析，结果如图19～图22所示.

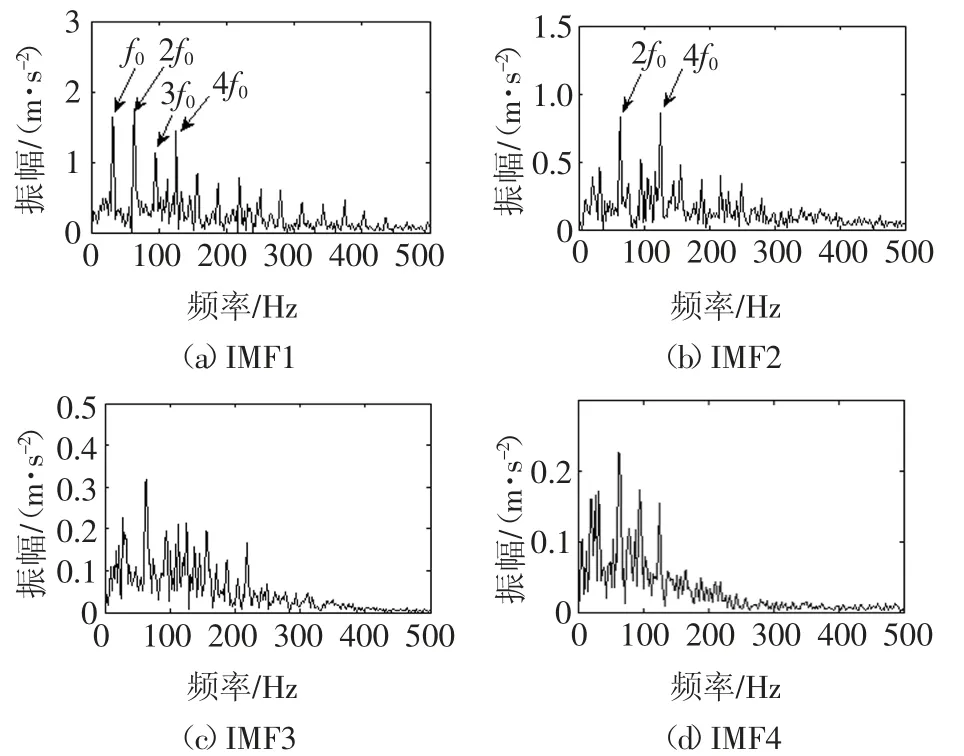
图19 实验信号EMD分解分量的包络谱图Fig.19 The envelope spectrum of EMD decomposition components of the experimental signal

图20 实验信号LCD分解分量的包络谱图Fig.20 The envelope spectrum of LCD decomposition components of the experimental signal

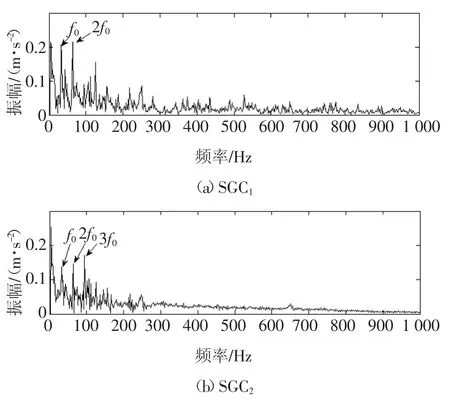
图21 实验信号SGMD分解分量的包络谱图Fig.21 The envelope spectrum of SGMD decomposition components of the experimental signal

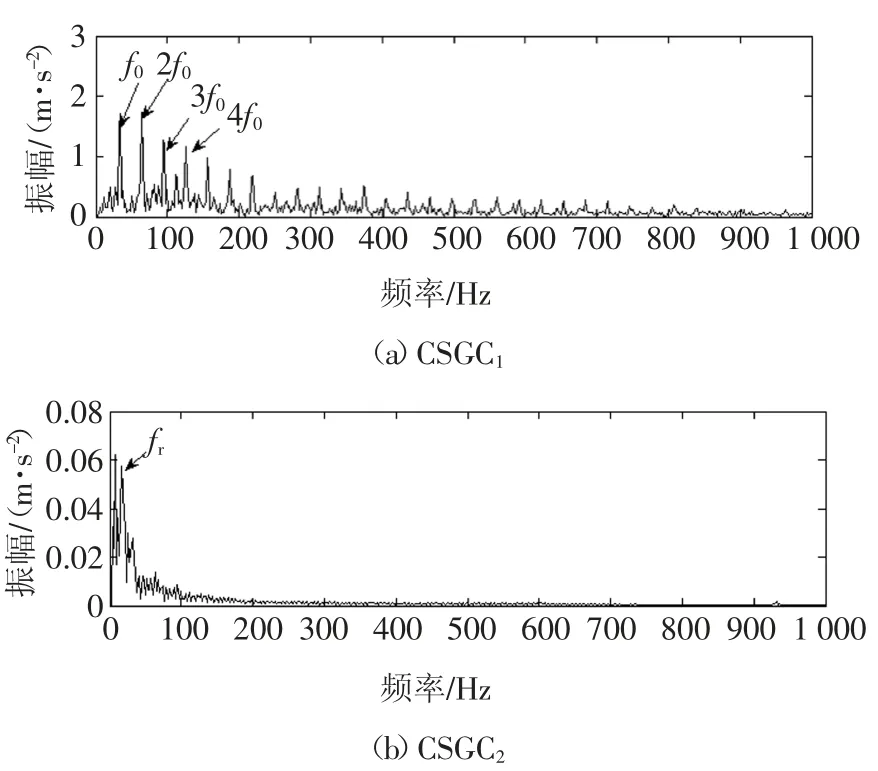
图22 实验信号ISGMD分解分量的包络谱图Fig.22 The envelope spectrum of ISGMD decomposition components of the experimental signal

从图19～图22可以看出，图19、图20、图21中提取出了轴承故障特征频率，而齿轮故障特征频率被完全覆盖；图22中同时提取出了齿轮和轴承故障特征频率.对比可知，ISGMD方法在复合故障诊断方面优于EMD、LCD和SGMD方法，ISGMD方法是一种较好的复合故障诊断方法.

4 结论

本文提出了一种改进的辛几何模态分解方法，采用了层次聚类方法对SGMD方法进行改进，使其能够自适应地进行分量重组，并将其应用于复合故障诊断中.通过对复合故障仿真信号和实验信号分析并将ISGMD方法和EMD、LCD、SGMD方法对比，结果表明ISGMD方法能更好地识别复合故障.