小型微带圆环形结构双模带通滤波器设计
2020-03-02姬五胜周祥伟赵思雨
戴 薇,姬五胜,周祥伟,赵思雨
(1.天津职业技术师范大学电子工程学院,天津 300222;2.天津职业技术师范大学天线与微波技术研究所,天津 300222)
在无线通信系统中,微波滤波器作为一种必不可少的无源器件,其性能关系到整个无线通信系统的质量。随着通信技术的快速发展,实现小型化、高选择性的微波滤波器日益引起研发人员的重视。双模滤波器在实现小型化的同时,具有成本低、质量轻、损耗低等优势,尤其受到设计者的青睐。
微波滤波器的“双模”思想最早由德国科学家Wolff[1]于1972 年提出,他在环形谐振器的馈电处引入微扰,实现了“双模”的分离。1995 年英国科学家Hong利用方形环设计出一种全波长的双模带通滤波器。日本的Makimoto 等[2]利用阶跃阻抗环形谐振器设计出一种双模带通滤波器,并提出双模滤波器的3 个设计准则。此后,双模滤波器的研究进入了黄金时代。文献[3]在矩形环谐振器的上下两侧分别引入短路和开路微扰,在不增加滤波器设计尺寸的前提下,增加谐振模式数量。文献[4]在矩形环谐振器的4 个边中点向环中心压缩,形成压缩双模环形双通带滤波器,进一步缩小滤波器体积,但介质基板性能不佳,电路测试插入损耗和回波损耗较大。文献[5]在方形环谐振器的4 个直角处引入方形贴片和切口微扰,滤波器通带两侧均产生传输零点,通带选择性提高。文献[6]在方形谐振器对角线处开2 个不等长的T 形十字槽微扰,有效减小滤波器尺寸并减小辐射损耗。文献[7]应用折叠的阶跃阻抗谐振器形成十字形双模双通带滤波器,但2 个通带带宽较窄,且第二通带选择性不高。文献[8]在六边形环形谐振器几何中心处加载对称枝节,激发谐振器内一阶简并模的分裂,实现多种模式谐振。文献[9]通过调整圆环形谐振器开路微扰个数,激发不同简并模式协同工作,形成多通带,提高信道使用效率,但通带带宽较窄,选择性较差。文献[10]通过改变圆环形谐振器的输入、输出馈电线间耦合角度,实现三通带,但仍存在通带带宽较窄、选择性不好的问题。文献[11]在半圆环形谐振器内部引入T 型微扰结构,增加双模滤波器的设计自由度,且输入输出馈电线与谐振器共用一个圆心,在通带两侧产生传输零点,通带选择性高,但Rogers 5880 介质基板硬度不高,也没有提供实物电路。上述设计均存在一定缺陷,本文通过在圆环形谐振器上加载短路枝节、开路枝节微扰结构,同时对弧形耦合馈电结构进行激励,完成圆环形双模带通滤波器的设计。对比文献[9-11],该带通滤波器通带选择性好,通频带中心频率处在工信部5G 规划的4.8~5.0 GHz 频段[12],在5G 通信中具有应用前景。
1 电路结构设计
圆环形双模带通滤波器为单层介质结构,有2 个金属层和1 个介质层。顶层为微带贴片金属层,底层为金属接地面,顶层与底层之间通过一对通孔穿过介质层连接。顶层金属层由圆环形双模谐振器与弧形耦合馈电结构构成,其拓扑结构如图1 所示。

图1 圆环形双模滤波器的拓扑结构
环形结构谐振器因环形结构的封闭性可使微带分布连续,产生多条信号通路,多条通路上的信号通过叠加产生简并模电路特性[13]。本文通过在圆环形谐振器内加载微扰单元,激发一对简并谐振模式并将其分离,形成双模工作方式,从而实现双模谐振器。加载的短路枝节与开路枝节微扰单元如图1 所示,2 种微扰结构的引入呈轴对称分布;为了增强滤波器的耦合度和降低插入损耗,在输入输出微带馈电端又加载一对弧形开路枝节,同时在弧形开路枝节末端处加载一段弧形微带线。
2 仿真结果及电路特性分析
2.1 双模谐振器的谐振分析
根据奇偶模分析法,任何一个微波信号均可等效为1 个奇模信号和1 个偶模信号的叠加[14]。圆环形双模谐振器等效电路如图2 所示。利用电路的线性叠加理论对双模谐振器进行分析,在图2(a)中,从中间对称面可将二端口网络分成2 个对称部分。当二端口网络奇模激励时,对称线处的电压为0,等效为理想电壁,中间的对称面相当于加载一个短路面,其等效电路如图2(b)所示。当二端口网络偶模激励时,对称线处的电流为0,等效为理想磁壁,中间的对称面相当于加载一个开路面,等效电路如图2(c)所示。
在奇模激励下,从馈电端看奇模的输入导纳为[15]

同理,偶模的输入导纳为[15]
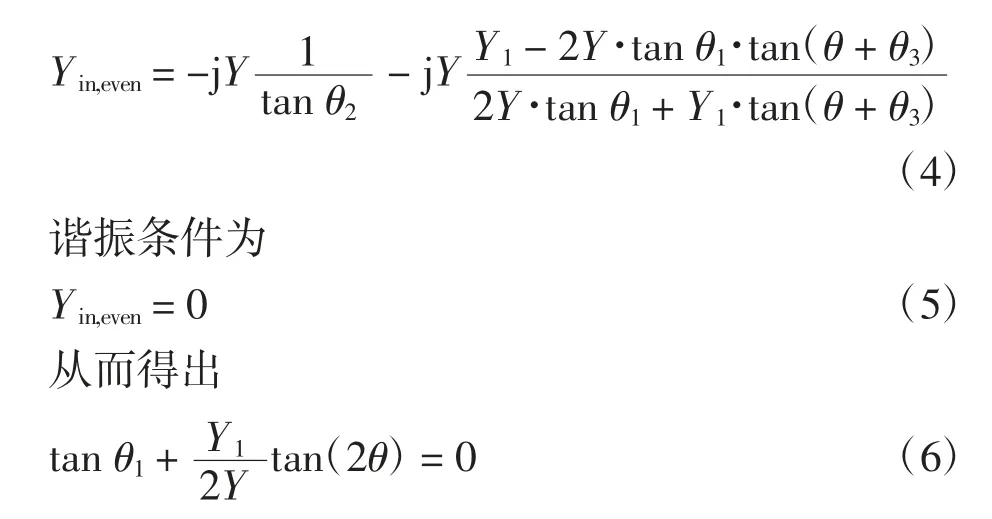
式(3)和(6)表明,微扰尺寸(θ1)仅对偶模产生影响,而对奇模无影响。
上述结论可在图3 中得到验证。
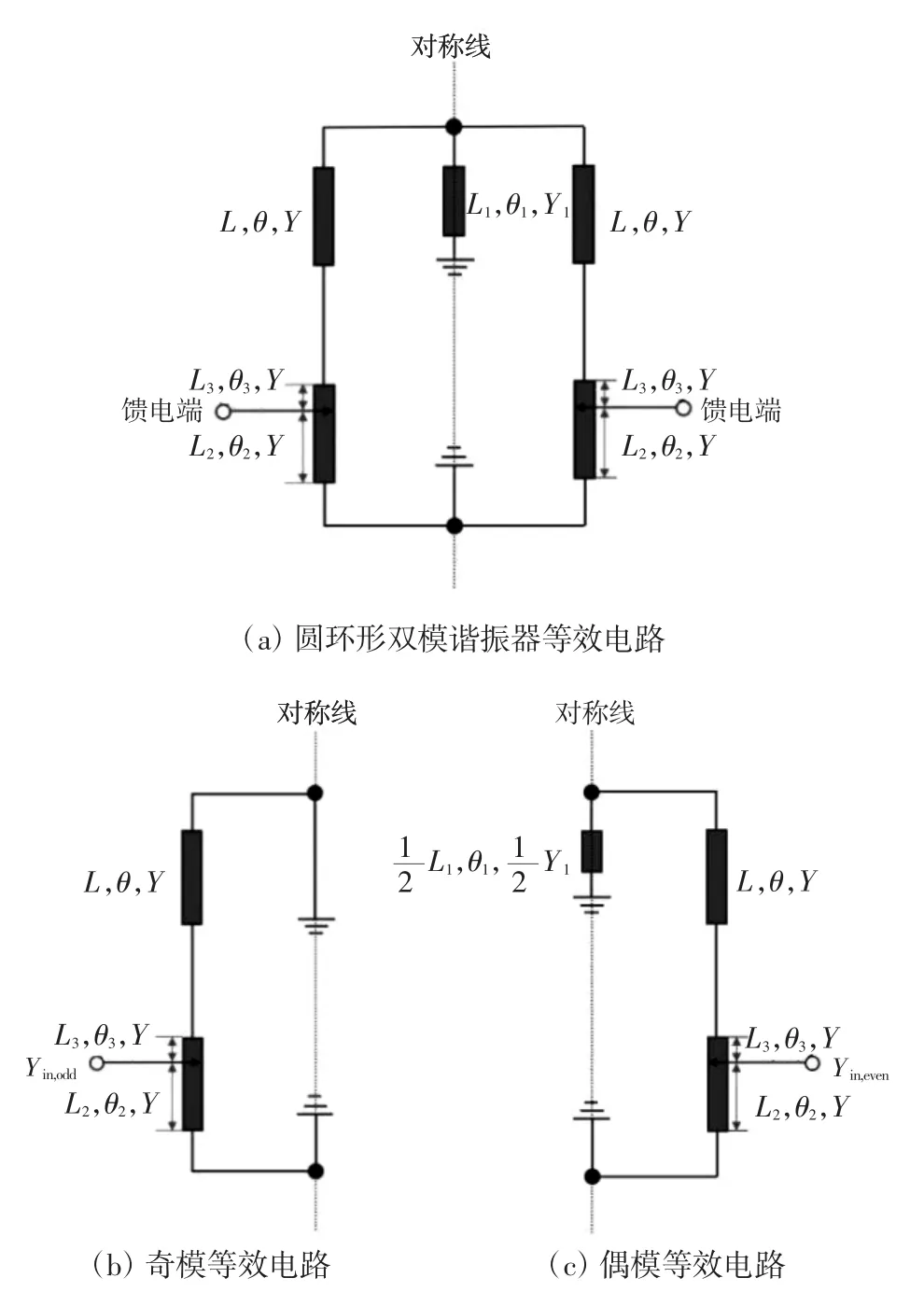
图2 圆环形双模谐振器等效电路
图3 为弱耦合下圆环形双模谐振器偶模电流和奇模电场分布图。由图3(a)可以看出,当谐振器在偶模模式下,短路枝节和开路枝节微扰结构处的电流最小,微扰结构的引入对偶模谐振频率产生影响;由图3(b)可以看出,当谐振器在奇模模式下,等效电路短路枝节微扰不存在;开路枝节微扰结构处的电场最小,此时可等效为短路,本质上该开路枝节微扰结构的引入不会对奇模的谐振频率产生影响。
利用ANSYS 公司的三维高频电磁仿真软件HFSS-15 仿真,在弱耦合馈电方式下,通过改变微扰结构参数,研究圆环形双模谐振器谐振频率的变化规律。短路枝节微扰结构对圆环形双模谐振器简并模谐振频率的影响如图4 所示。
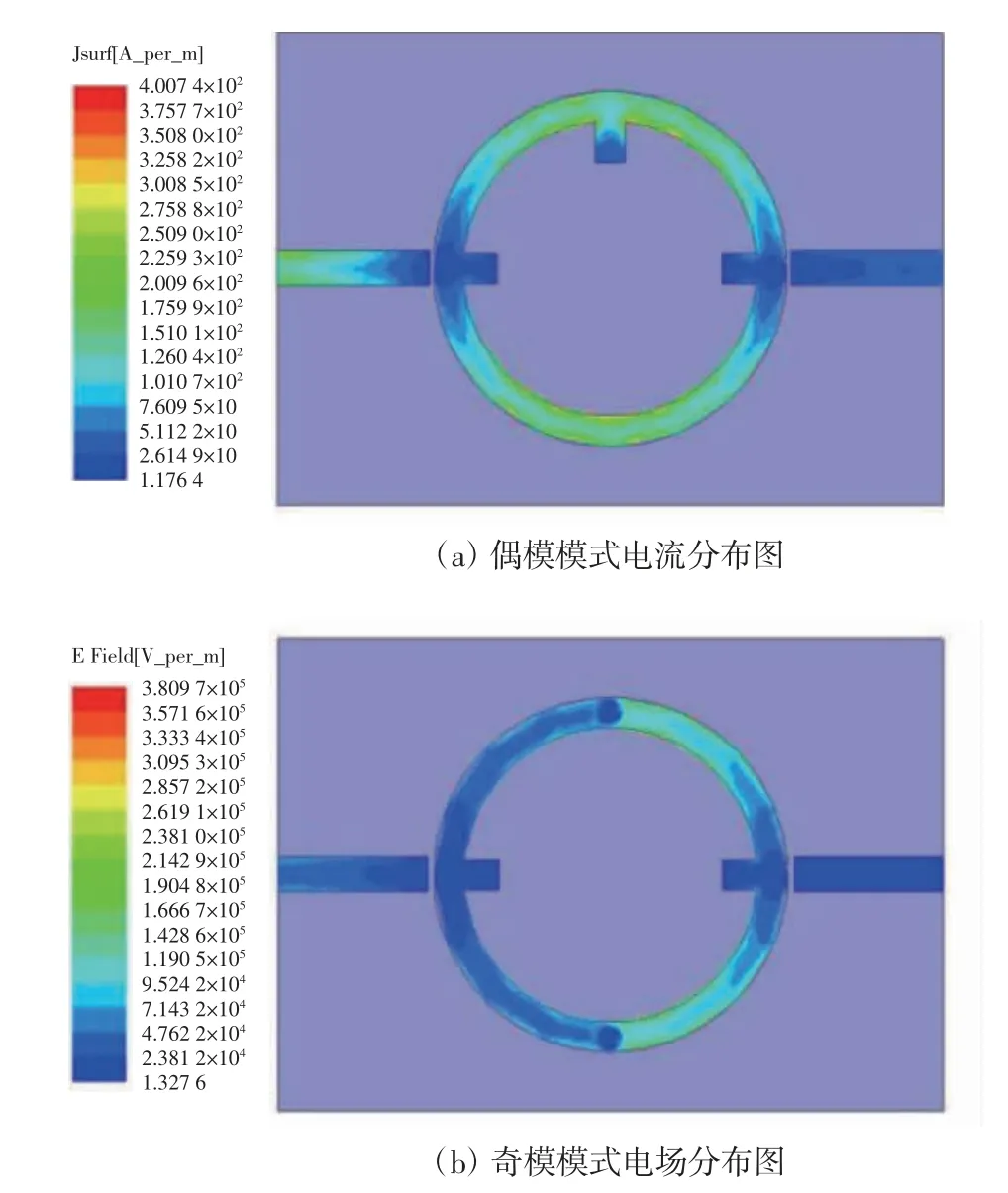
图3 弱耦合下圆环形双模谐振器偶模电流和奇模电场分布图
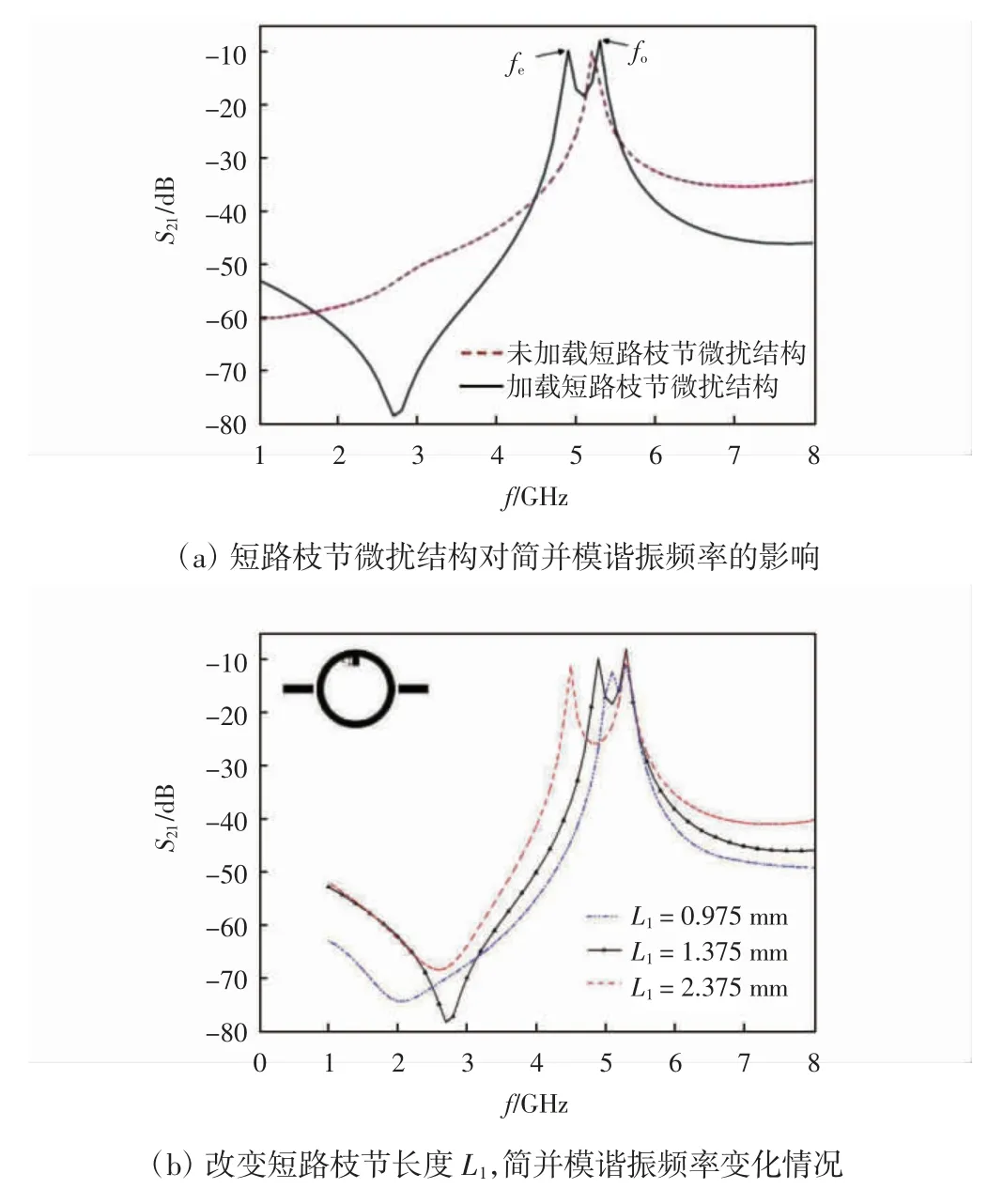
图4 短路枝节微扰结构对圆环形双模谐振器简并模谐振频率的影响
图4(a)中,在未加载微扰结构时谐振器的双模工作方式未被激发,一对简并模式尚未分离,它以相同的谐振模式工作,无法产生通带;而在短路枝节微扰的作用下,一对简并模式实现了分离,2 个谐振频率分别为奇模谐振频率fo和偶模谐振频率fe,形成了通频带。在图4(b)中,通过改变短路枝节长度L1,分析简并模谐振频率变化情况。可以看出,随着短路枝节长度的增大,通频带的宽度逐渐变宽。这是由于改变短路枝节长度可以调节谐振器中一对简并模式的分离程度,从而使通带宽度发生变化。
在加载短路枝节微扰结构基础上,再加载开路枝节微扰结构,取其长度L2分别为1.175 mm、2.175 mm和3.175 mm 进行仿真,圆环形双模谐振器简并模谐振频率变化情况如图5 所示。

图5 改变开路枝节长度L2,圆环形双模谐振器简并模谐振频率变化情况
从图5 可以看出,随着开路枝节长度增大,圆环形双模谐振器简并模谐振频率向左偏移,通带的中心频率逐渐变小。这是由于改变开路枝节长度可以调节奇偶模谐振频率,从而影响通带的中心频率。此外,在添加了开路枝节微扰结构后,谐振器的通带处产生了传输零点。如果在入射端分别入射顺时针和逆时针2种行波,在某一频率下,这2 种行波到达输出端时,若相位相反即可相互抵消,可产生传输零点[13]。双模圆环形谐振器可以产生多条信号通路,这些信号通过叠加产生传输零点。
2.2 馈电结构分析
双模滤波器由双模谐振器和馈电结构组成。加载合适的馈电结构,可实现馈电端与双模谐振器之间的良好电磁耦合,实现有效的滤波。当采用弱耦合馈电方式时,源和负载之间不能实现强耦合,滤波器性能较差。本文在谐振器输入输出微带馈电端分别加载一段弧形开路枝节,通过增加耦合边长实现增强源和负载之间的耦合度;同时在这弧形开路枝节的末端处加载一小段弧形微带线,进一步增强耦合度,降低插入损耗。
2.2.1 弧形开路枝节对滤波器性能的影响
当弧形开路枝节弧长变化时,圆环形双模滤波器S21参数也随着发生变化。取弧形开路枝节弧长为3.23 mm、6.46 mm、9.69 mm 进行仿真试验,圆环形双模滤波器谐振性能的变化HFSS 仿真结果如图6 所示。从图6 可以看出,随着⌒m的增大,源和负载的耦合度变强,实现对谐振器的强激励。
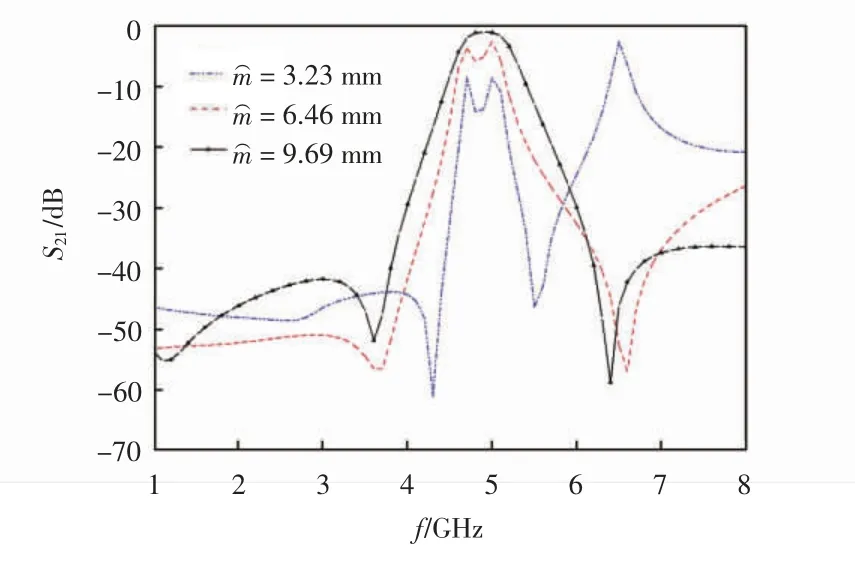
图6 改变弧形开路枝节弧长,圆环形双模滤波器谐振性能的变化HFSS 仿真结果
2.2.2 弧形微带线对滤波器性能的影响
图7 为加载弧形微带线前后圆环形双模滤波器S参数的变化情况。从图7 可以看出,当加载弧形微带线后,通带上下边缘处的2 个传输零点间的距离变近且其两侧的陡峭度变好,表明一对弧形开路枝节末端之间的耦合度增强,滤波器的通带选择性提高。但滤波器S11曲线上2 个传输极点消失,性能变差。

图7 弧形微带线长度对圆环形双模滤波器S 参数的影响
2.2.3 弧形开路枝节与谐振器间的耦合角度对滤波器性能的影响
滤波器性能也受到弧形开路枝节与谐振器间的耦合角度的影响。仿真实验发现,当弧形开路枝节与谐振器共用一个圆心时,滤波器的带宽较窄且插入损耗S21和回波损耗S11均较大,但当弧形开路枝节的圆心稍稍偏移谐振器的圆心时,滤波器的性能会变好。由于当弧形开路枝节的圆心偏移谐振器的圆心时,源和负载间耦合间距减小,弧形开路枝节末端与谐振器顶部耦合度增强。共用/不共用圆心时,圆环形双模滤波器电场分布图如图8 所示。从图8 可以看出,不共用圆心时,图8(b)电场强度比图8(a)略强。

图8 共用/不共用圆心时,圆环形双模滤波器电场分布图
HFSS 仿真发现,当弧形开路枝节和圆环形谐振器边缘的耦合间距变化时,滤波器的性能也随之发生变化,耦合间距s 对圆环形双模滤波器S 参数的影响如图9 所示。当耦合间距s 为0.358 mm 时,滤波器的工作状态最佳。

图9 耦合间距s 对圆环形双模滤波器S 参数的影响
2.3 仿真结果与实物测试
经过仿真及优化,得到滤波器性能最优参数值如表1 所示。表中,环形谐振器内短路枝节长为L1,短路枝节通孔半径为R6,开路枝节长为L2,环形谐振器内环和外环半径分别为R0和R1,环宽为a;弧形耦合馈电结构内弧形开路枝节内环和外环半径分别为R2和R3,环宽为b,弧长为⌒m,弧形开路枝节末端与环形谐振器间距为g,输入输出微带馈电宽为c,输入输出微带馈电与环形谐振器间距为s;弧形微带内环和外环半径分别为R4和R5,环宽为b,弧长为⌒n,弧形微带与弧形开路枝节末端间距为k。滤波电路及其仿真测试结果如图10 所示。从图10(a)可以看出,电路的整体尺寸为16 mm×22.49 mm×0.508 mm。电路的电介质材料为罗杰斯板RO4003,介电常数为εr=3.55、损耗正切为tan δ=0.002 7,电介质层厚度为h=0.508 mm。

表1 设计的滤波器性能最优参数值

图10 滤波器电路仿真及测试结果
利用HFSS 软件对滤波器进行仿真,得到结果为:滤波器3 dB 通带范围为4.65~5.18 GHz,中心频率为4.9 GHz,分数带宽为11%,带内插入损耗S21优于-0.94 dB,回波损耗S11优于-28.3 dB,通带上下边缘处各有一个传输零点,分别位于3.6 GHz 和6.4 GHz 处,体现出电路的良好性能。
利用矢量网络分析仪AV3629 对电路实物进行测试,与HFSS 软件仿真结果进行对比。从图10(b)可以看出,测试结果为:滤波器3 dB 通带范围为4.67~5.11 GHz,中心频率为4.89 GHz,分数带宽为9%,较仿真结果存在约2%的误差;带内插入损耗S21优于-1.9 dB,回波损耗S11优于-24 dB,与仿真结果相比,S21存在约0.96 dB 的误差,S11存在约4.3 dB 的误差;通带下边缘处的传输零点位于3.6 GHz 处,与仿真结果一致,但通带上边缘处的传输零点位于6.6 GHz 处,较仿真结果存在约0.2 GHz 的误差;此外,在通带内产生了2 个传输极点,分别位于4.79 GHz 和4.96 GHz处,测量结果较仿真结果有所优化。测试与仿真结果基本一致,误差在可控范围内。
测试和仿真结果存在一定的误差,主要由于滤波器电路加工精度不够、SMA 接头手工焊接引入损耗等所致。另外,在使用仿真软件时,把各微带线间的电场干扰理想化,只考虑被定义的耦合线间的耦合关系,忽略没有定义为耦合关系的各微带线间的实际耦合。在实际中,一定距离内各微带线之间都有耦合关系,这也是造成仿真结果与测试结果之间存在误差的原因。
3 结语
本文通过在圆环形谐振器内部加载短路枝节与开路枝节微扰,在输入输出微带馈电端加载弧形开路枝节,并在弧形开路枝节末端加载一段弧形微带线,实现一款小型化的圆环形双模带通滤波器。改变微扰结构参数,可实现通带带宽和中心频率可调,具有一定的设计灵活性;优化弧形开路枝节和弧形微带线等参数,可降低带内插入损耗,产生传输零点,提高通带的选择性。该滤波器结构简单、体积小、成本低、带内性能好,在Sub-5G 频段有应用前景。但该滤波器也存在一些不足,如通带可调的范围有限,3 dB 分数带宽较窄,因此其宽带化有待进一步研究。
