基于因子分解机的月售电量预测模型

王安东，王东涛，叶剑华

（1.天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津 300222；2.天津职业技术师范大学自动化及电气工程学院，天津 300222）

月售电量是电力公司业绩考核和行业对标的一项重要经济指标。月售电量反映了电力企业的售电能力和综合管理水平，因此受到了各级电力企业的普遍关注。准确的月售电量预测可为企业制定电力规划、售电计划和设备检修计划等提供依据，保障电力企业正常运行，降低企业运行成本，从而提高电力企业的经济效益和社会效益。因此，提高月售电量预测的精度具有十分重要的现实意义。国内外一些学者针对月售电量预测方法进行了研究，提出了多种预测方法，如石秀倩等[1]使用BP 神经网络分析预测法并引入温度因素和时间负荷因素对用户用电负荷进行预测；苏振宇等[2]使用Holt-Winters 方法对完成季节调整的数据进行预测并采用回归法预测月度负荷；马婉贞等[3]使用改进型灰色理论方法在经典灰色理论基础上采用三点平滑法对数据进行前期处理并构建等维度新信息矩阵的GM（1，1）模型，最终完成负荷的预测。采用最小二乘回归法建立的月售电量与其主要影响因素（经济因素）之间的回归模型，虽然能提高预测精度，但增加了数据收集的难度。灰色理论法对数据质量要求较低，但仅对指数变化的数据预测结果较为准确，且受外界干扰较大。用神经网络分析预测法预测精度很高，但该方法需要庞大的数据量作为样本[4]。张强等[5-7]采用时间序列差分自回归移动平均模型（autoregressive integrated moving average model，ARIMA）预测月售电量，该模型根据历史数据变化规律建模，预测变化趋势明显的年度电量有较高的精度，而直接用于预测波动较大的月售电量则会有较大的误差。

月售电量受到外界影响较大，如季节变更、突发事件及经济变化等。从现有的预测结果来看，一季度3个月的预测误差显著偏大。原因是春节期间各行各业放假，工厂普遍停工停产，春节期间的电力负荷与平日有很大的不同，由此对一季度的月售电量预测产生了很大的影响。而传统的月售电量预测方法没有考虑到该因素对售电量预测精度的影响，导致了预测结果误差较大。程超[8]将历史的月售电量序列转换为春节全分布在2 月时的新序列，并将新序列参与建模与预测，最后将该预测值按预测当期的实际春节分布逆转换为实际的月售电量预测值。这种方法虽能够减少春节的不同分布对月售电量的影响，但预测误差还有进一步减小的空间。刘建等[9]提出分行业售电量占比预测值以及待预测年份及历年的春节日期，对月度售电量进行调整，从而考虑春节对售电量的影响。为提高月售电量的预测精度，本文将X12 季节调整模型的原始数据进行分解，采用ARIMA 模型和历史同期平均法分别预测分量，通过计算得到初步预测结果，利用拟合模型对初步预测结果进行修正，从而得到精度较高的预测结果。

1 计及ARIMA 的月度售电量模型设计

1.1 Cencus X12 季节调整模型

月度售电量一般包含3 个变量因素，分别为趋势分量（seasonal trend-cycle，TC）、季节分量（seasonal factors，SF）以及随机分量（irregular component，IR），三者的变化轨迹不同，所以在售电量预测中，如果对此3 个分量不加以分离而直接预测，会造成分量间相互影响，导致月度售电量预测精度降低。

本文采用X12 季节调整乘法模型对月度售电量进行分解，其基本原理为：在移动平均法的基础上，增加加权系数，通过移动加权系数平均法，对月度售电量的时间序列数据进行逐项分解，从而达到分解月度售电量原始时间序列的目的。X12 乘法模型已经嵌入到Eviews 软件的“季节调整”功能中，可以通过软件实现对月度售电量的分解，将其分解为3 个变量，其分解公式为

式中：E 为月度售电量的时间序列；ETC为月度售电量的趋势分量序列；ESF为月度售电量的季节分量序列；EIR为月度售电量的随机分量序列。

1.2 计及ARIMA模型的趋势分量预测模型

ARIMA 模型是一种时间序列预测方法。其主要原理为：将非平稳的时间序列数据转换为平稳的时间序列过程，将因变量仅对其滞后值以及随机误差项的现值和滞后值进行回归，建立预测模型。ARIMA 模型由自回归模型AR 和移动平均模型MA 组成。自回归模型AR 用来确定当前值和历史值之间的关系，通过变量自身的时间数据来对自身进行预测，且自回归模型AR 必须满足平稳性要求；自回归模型AR 需要确定1个p 值，即表示使用p 期历史数据来预测当前值，自回归模型AR 当前值为

式中：μ 为常数项；p 为AR 模型阶数；γi为自相关系数；∊t为误差值。

移动平均模型MA 主要用来进行自回归模型中的误差项的累积，可有效消除模型预测中的随机波动，MA 模型当前值为

式中：θi为移动平均系数；q 为MA 模型阶数。

将自回归模型AR 与移动平均模型MA 组合可以得到ARMA 模型，即自回归移动平均模型

采用ARIMA 模型进行趋势分量TC 预测的步骤：①进行原始序列平稳化，使用ADF（augmented dickey-fuller test）检验法对原始序列进行d 阶差分并判定其稳定性，确定差分次数d；②通过自相关系数和偏自相关系数的截尾及拖尾特性来确定模型阶数p、q；③使用最小二乘法算法计算模型中除p、d、q 外的其他参数；④编写程序，输入p、d、q 参数，进行趋势分量TC 预测。

1.3 季节分量SF和随机分量IR预测模型

调整后观察季节分量SF 发现，季节分量SF 序列具有较好的周期性，且历史年份的同期月季节分量波动很低，具有一定的平衡性，因此采用历史同期数据平均值法预测季节分量SF，计算公式为

式中：SFi，j为第i 年第j 月的月度售电量的季节分量。

月度售电量的随机分量没有明显的规律，本文取历史同期随机分量的平均值作为当期月度售电量的随机分量。

随机分量IR 的预测计算公式为

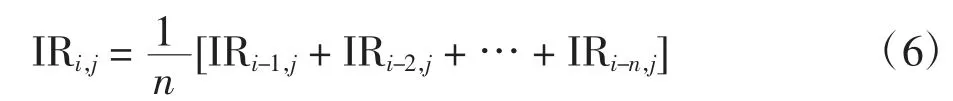
式中：IRi，j为第i 年第j 月的月度售电量的随机分量。

2 计及春节调整因素与因子分解机的预测结果修正模型

2.1 春节调整因素分析

季节的变更会对售电量预测结果造成较大的影响。由于春节是中国的新年，且每年春节的阳历时间并不相同，春节期间又会出现商家停业、工厂停工及春运等情况，所以春节期间售电量预测准确度的提高，能对月度售电量预测的整体准确度提高有很大的帮助。

本文选择占季比（历年1—3 月份每月历史售电量分别占历年第一季度比重）作为月度售电量预测的春节修正方式。某地市2013—2018 年第一季度售电量占季比如图1 所示。2013—2018 年春节日期分别为2 月10 日，1 月31 日，2 月19 日，2 月8 日，1 月28 日和2 月16 日。从图1 可以看出，春节日期越早，1 月份占季比越小，3 月份占季比越大，可见春节日期对于第一季度单月售电量占比有很大影响。

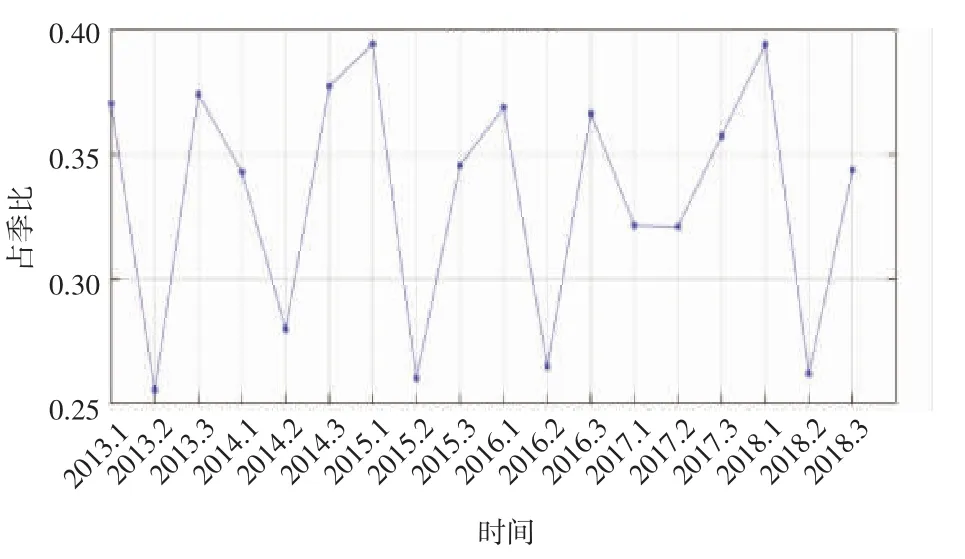
图1 某地市2013—2018 年第一季度售电量占季比

2.2 因子分解机模型及其实现

因子分解机（factorization machine，FM）[10]是一种基于矩阵分解的机器学习算法，相较于传统的线性模型，FM 算法在线性模型中增加了新的交叉特征及其对应的权值[11]。

在春节因素与占季比的原数据集中，输入为当月首日距春节时长和月份，输出为占季比，针对这2 个特征间的关系给出因子分解机模型[12]

式中：ω0为最初权值/偏置项；ωi为每个特征xi对应的权值；f（x）为当特征为xi时模型的输出；vi为系数矩阵V 的第i 维向量；＜vi，vj＞为向量vi，vj的点积。

上述系数矩阵V 为

由式（7）可以看出，交叉特征项的计算较为复杂。为降低其计算复杂度，对交叉特征项进行化简[13]

式（9）将交叉特征项进行化简后，对本文这一回归问题的损失函数[14]为

式中：f（x）可以作为回归中的预测结果；y 为真实输出结果；p 为样本个数。

可以通过对损失函数LossFuncR的输入量θ（分别为常数项、一次项、交叉特征项）求导计算出梯度，然后根据梯度对权值更新。梯度计算式如下

由式（7）—式（11）可知，本文所述的因子分解机（FM）算法程序流程如图2 所示。

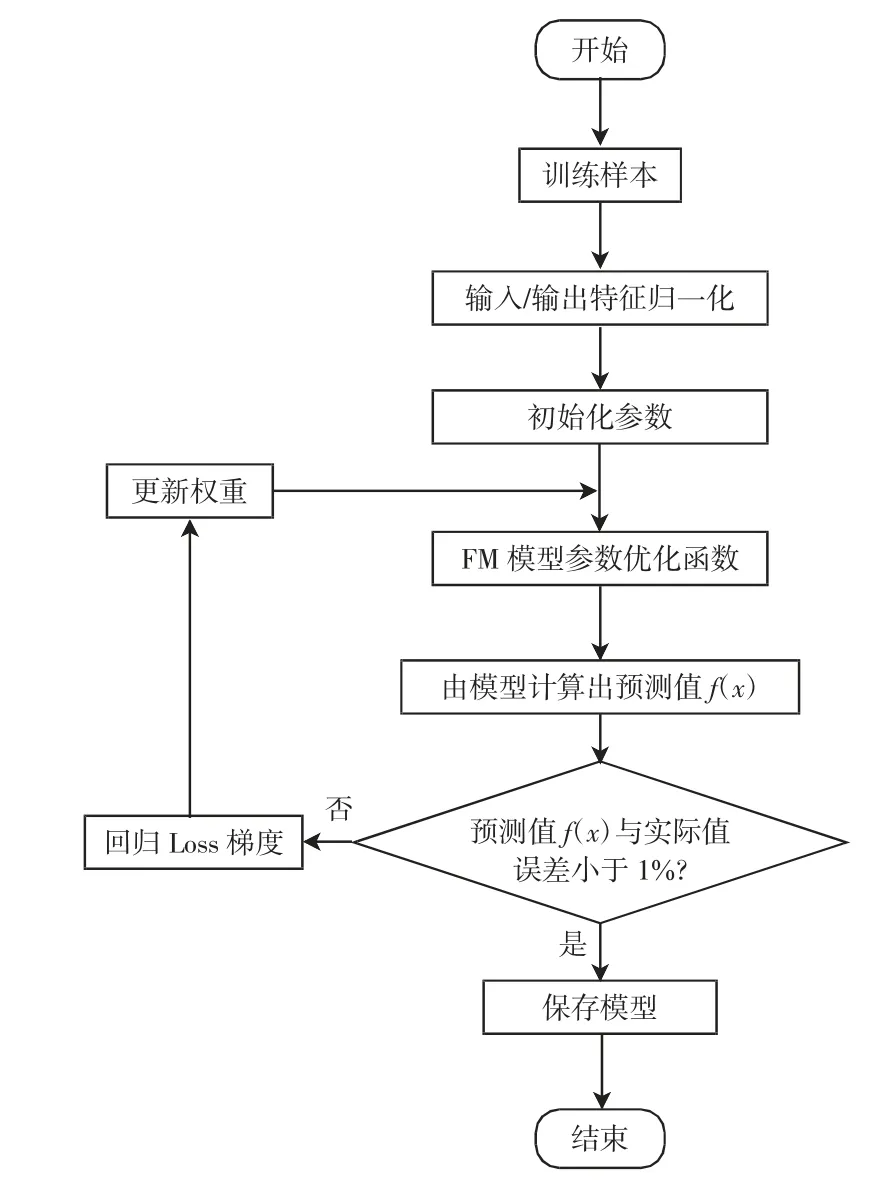
图2 因子分解机（FM）算法程序流程

因子分解机（FM）算法计算步骤：①运行min-max归一化将训练数据特征归一化并将模型参数ω0、ωi、vi初始化；②运行如式（7）、（9）所示FM 算法模型，优化模型参数并计算预测值f（x）；③判断真实值y 与预测值f（x）的误差是否小于1%，若小于1%，保存模型并结束算法，若大于1%，通过式（10）、（11）对损失函数LossFuncR的输入量θ 求导，计算梯度，并更新权重直至误差小于1%。

3 算例分析

3.1 历史数据

本文使用2013 年1 月—2018 年12 月的月度售电量数据预测2019 年全年月度售电量。某地级市月度售电量如表1 所示。

3.2 结果分析

2013 年1 月—2018 年12 月售电量数据曲线如图3 所示。

（1）总售电量及各分量变化趋势

将售电量数据分解为趋势分量TC、季节分量SF及随机分量IR，售电量分解图如图4 所示。

由图4 可知，趋势分量Y_TC 呈现明显上升趋势，季节分量Y_SF 周期性变化，随机分量Y_IR 变化无规律。

（2）考虑季节调整的预测结果

采用第2 节的方法对3 种分量进行预测，预测结果如表2 所示。

从表2 的售电量预测情况看，售电量预测值在2019 年的2、3 月份误差较大，其中3 月份超过6%，原因是预测时仅考虑季节调整因素，未考虑春节对1—3月份月度售电量的影响。

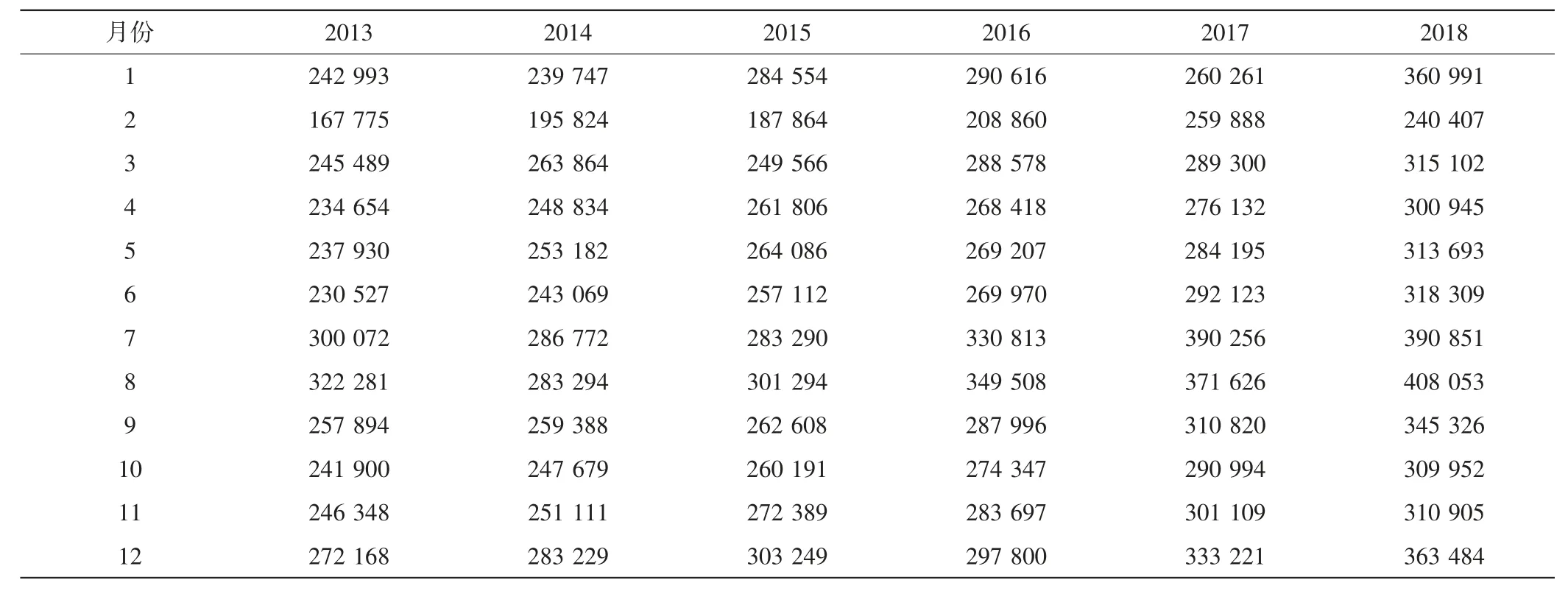
表1 某地级市月度售电量 ×104 kW·h

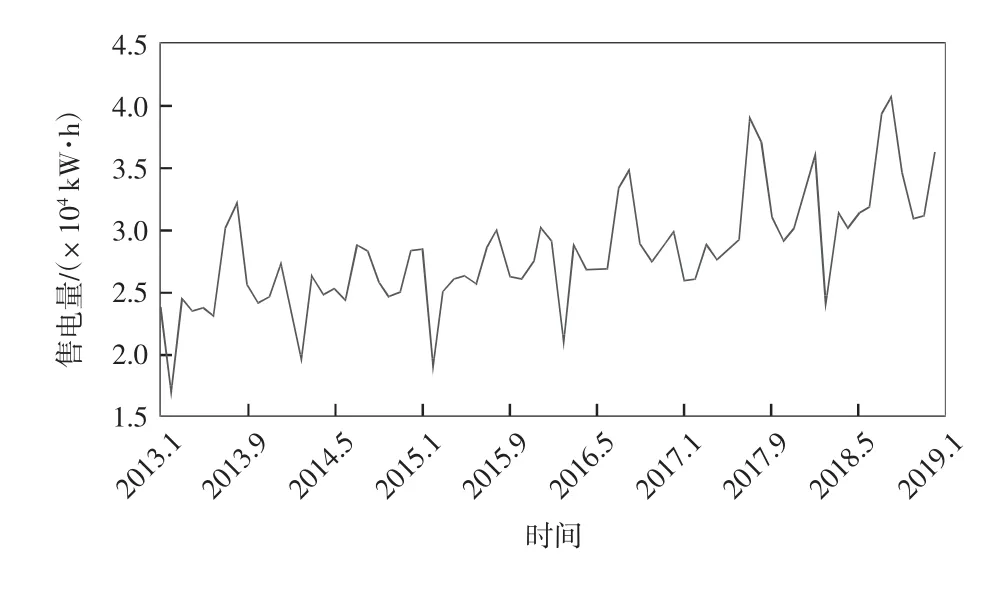
图3 2013 年1 月—2018 年12 月售电量数据曲线

图4 售电量分解图

表2 考虑季节因素的预测结果

（3）考虑春节因素的预测结果

根据2019 年春节日期及1—3 月首日到春节的时间、月份得到2019 年占季比，2019 年1—3 月预测占季比如表3 所示。

表3 2019 年1—3 月预测占季比

在初步预测完成后，由预测的1—3 月售电量总量和表3 给出的占季比，对2019 年1—3 月份预测结果进行调整，以提高预测精度。

考虑春节影响因素，重新进行月度售电量预测，结果如表4 所示。

表4 结果表明，在考虑了春节调整因素的影响后，1—3 月预测误差明显减小，平均误差降低。

（4）多种方法预测结果对比

将本文方法计算出的结果与传统的ARIMA 方法以及基于季节调整和H-P 滤波[15-16]的月度售电量预测方法进行了对比，对比结果如图5 所示。

从图5 可以看出，本文所使用的方法误差最小，7个月的平均误差达到了0.834 1%，且每月的误差均远低于同行业对标指标的5%，说明在月度售电量预测中，基于季节调整和春节调整的ARIMA 模型优于传统ARIMA 模型和基于季节调整与H-P 滤波的预测模型。

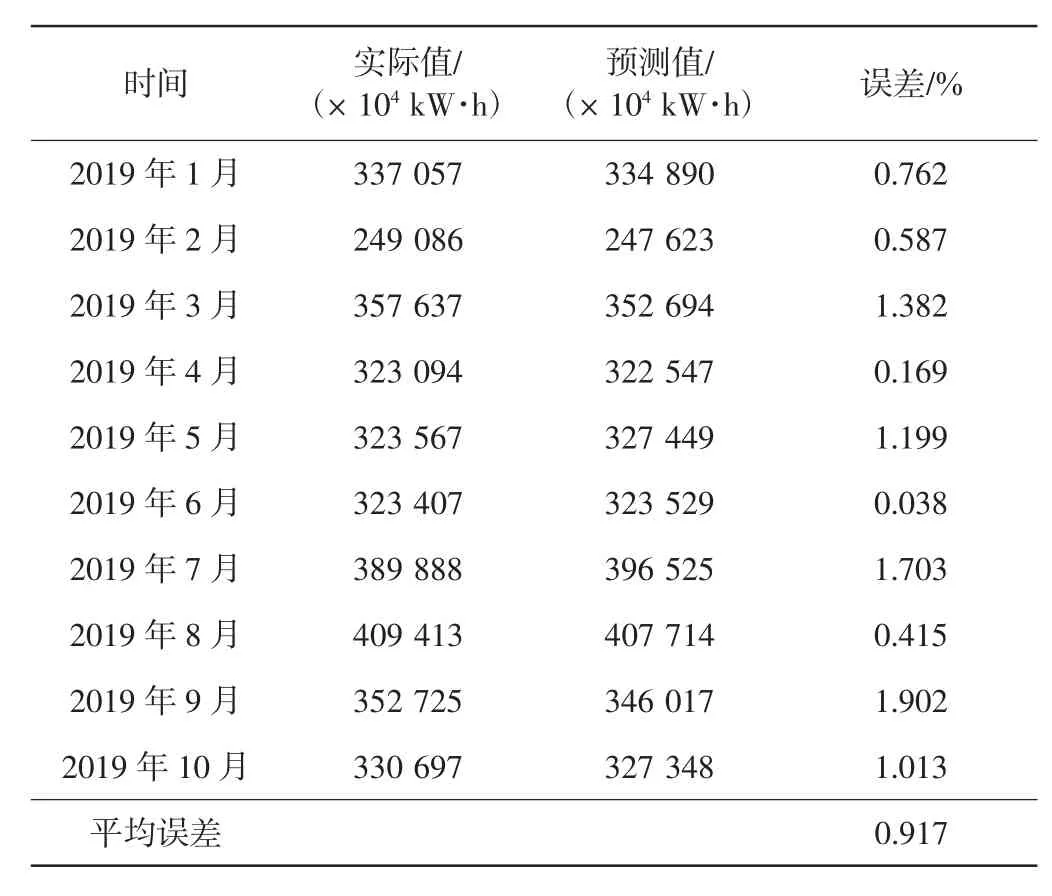
表4 考虑春节调整因素的预测结果

图5 3 种预测方法误差对比

4 结语

本文针对春节前后月度售电量预测精度较差的实际问题，提出了一种计及春节调整影响的基于因子分解机（FM）算法的月售电量预测模型。使用X12 季节调整模型将原始数据分解为趋势分量、季节分量和随机分量，采用ARIMA（p，d，q）模型和历史同期平均法分别预测趋势分量、季节分量和随机分量，对3 种分量进行乘积计算得到初步预测结果；计及春节调整影响因素，采用因子分解机算法对1—3 月首日距春节时长和占季比进行拟合，利用拟合模型对初步预测结果进行修正，提高了1 季度月售电量的预测精度。通过算例，验证了所提算法的有效性。