具有Bazykin 功能反应的捕食者-食饵模型

于 婕，孙福芹

（天津职业技术师范大学理学院，天津 300222）

在自然界中，物种并不是单独存在的。捕食者与食饵之间存在一种动态的关系，这种关系已经成为种群生态学的主要研究课题之一[1]。在种群生态学的研究中，由于其性态的复杂性和重要性，具有功能反应函数的捕食者-食饵模型被国内外的学者们广泛关注。功能性反应是描述每个捕食者每单位时间消耗的食饵数量的最关键因素之一。食饵种群的捕食功能反应是捕食者和食饵相互作用的主要因素，它描述了每单位时间内对于给定数量的食饵，捕食者所消耗的食饵数[2]。在相互作用的捕食者-食饵种群的动力学中，功能反应是决定不同动力学行为的一个重要方面。对于由食饵和捕食者所构成的2 种群相互作用的系统，最早被提出的是著名的Lotka-volterra 模型，但在该模型中，捕食者的数量与食饵的数量成正比，这与实际情况不符[3]。20 世纪50 年代末，Holling 在此基础上对不同的物种提出了3 种不同的功能反应函数，分别为HollingⅠ型、HollingⅡ型和HollingⅢ型功能反应，学者们对这3 类功能反应函数进行了广泛的研究[4-5]。

Holling 型功能反应只依赖于食饵种群，因此也被称为食饵依赖功能反应。基于不同的生物学背景，有不同的功能反应。Bazykin 型功能性反应用来描述捕食者饱和的破坏稳定力和争夺猎物的稳定力[6]。捕食者-食饵系统的动态是复杂的，在疾病的情况下，无论是捕食者还是食饵，还是在这2 种群中，复杂性都会增强[7]。因为疾病在自然界中很常见，不可忽略这一因素。因此，本文选用了Bazykin 型功能性反应的捕食者-食饵并考虑加入疾病这一因素，将捕食者分为易受感染的捕食者和已经被感染的捕食者2 类，将常见的二维系统模型变成三维系统模型，这一模型更加符合生物学实际背景。由于模型是一个三维系统，这给计算和分析带来了困难。本文通过Hurwitz 判据、Lyapunov 函数构造等技巧对所建三维模型的有界性、平衡点的存在性以及可行平衡点的局部稳定性和全局稳定性进行分析，并对数值模拟结果进行验证。

1 模型组成

考虑相互作用的物种食饵和捕食者的系统，x（t）为食饵种群的数量；p（t）为捕食者种群的数量，为建立捕食者-食饵系统的数学模型做出以下假设：

在没有捕食的情况下，食饵种群x（t）按logistic 增长方式增长，其内在增长率为r∈R+，环境承载力为k∈R+，有

在捕食的情况下，使用典型的捕食者-食饵模型[8]

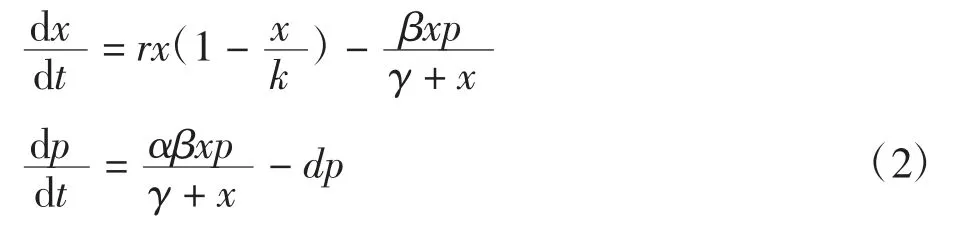
捕食者的功能反应遵循HollingⅡ型函数，γ 为其半饱和常数；β 为捕食者的最大捕食率；d 为捕食者的恒定自然死亡率；α 为食饵到捕食者的转化率（0 ＜α ＜1）。

在存在疾病的捕食者中，总捕食者种群p（t）被分为2 类，其中：y（t）为易受感染的捕食者的种群密度；z（t）为被感染的捕食者的种群密度。这种疾病只在捕食者中传播，易受感染的捕食者种群通过与感染性捕食者的接触以λ 的速率感染，遵循大规模行动定律λyz。基于上述假设，提出了以下数学模型

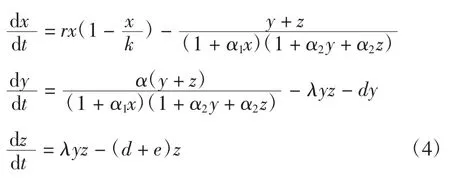
式中：e 为与疾病有关的额外死亡率。以上所有参数均为非负。

考虑到生物学意义，对系统（4）将在下列初始条件下进行分析

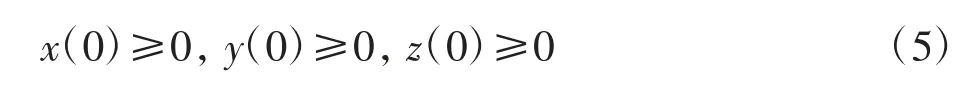
2 初步结果

2.1 有界性

定理1在R3+中，系统（4）具有正初始条件（5）的所有可行解都是一致有界的。

证明：令L（x，y，z）=x+y+z，则

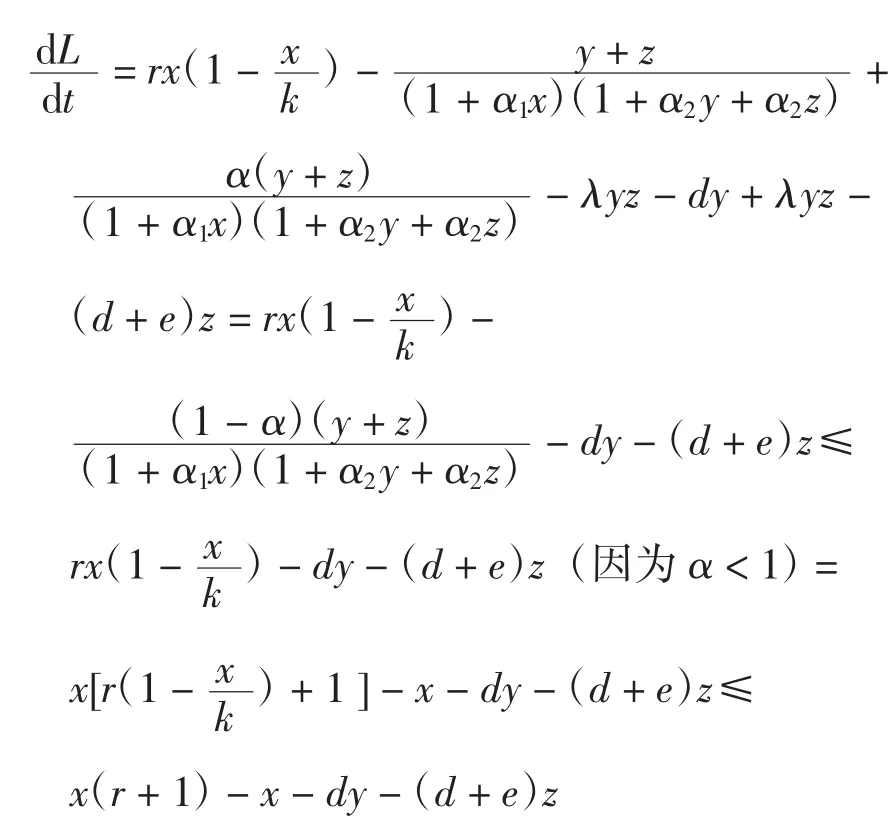
2.2 平衡点的存在性

通过求解x˙=0，y˙=0，z˙=0 得到了模型（4）的平衡点，系统（4）有平衡点E0（0，0，0），E1（k，0，0），E2（x2，y2，0），其中x2、y2可根据下面方程组（7）求解

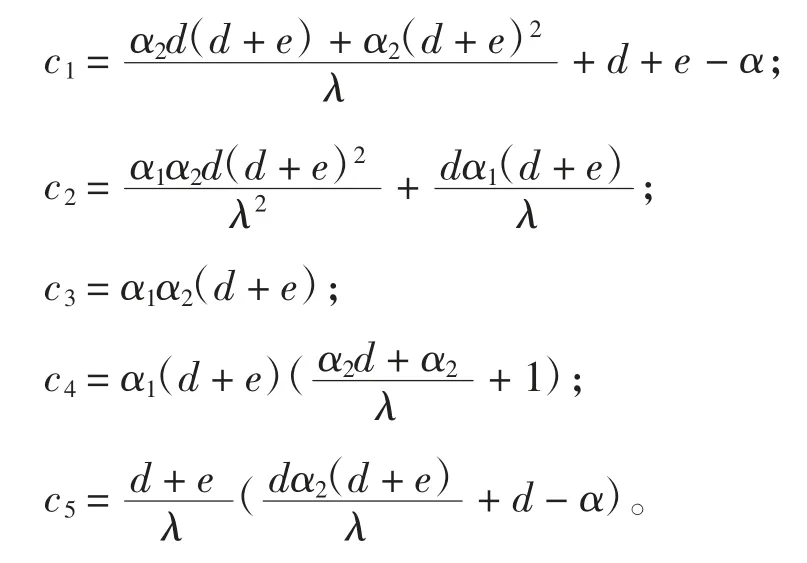
平衡点E0（0，0，0），E1（k，0，0）始终存在，当α ＞d（1+α1x2）时，E2（x2，y2，0）的平衡点是可行的。

3 稳定性分析

在本节中，讨论系统围绕每个平衡点E0、E1、E2附近的稳定性。系统在任意点（x，y，z）处的Jacobian 矩阵为J=（mij）∈R3×3。

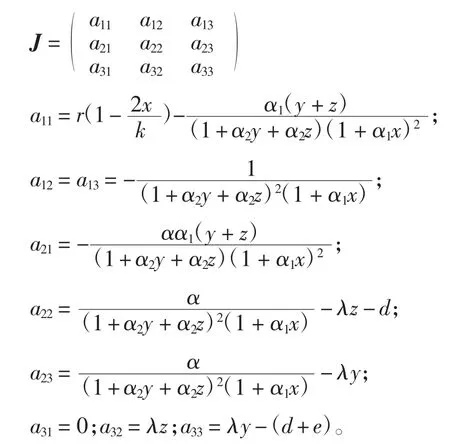
3.1 E0（0，0，0）的稳定性

设J0是系统（4）在平衡点E0处的Jacobian 矩阵，E0处的特征值为r、α-d 和-（d+e），由于r 为正，根据Routh-Hurwitz 的稳定性条件，E0是不稳定的。

3.2 E1（k，0，0）的稳定性

设J1是系统（4）在平衡点E1处的Jacobian 矩阵，E1处的特征值为-r、-d 和-（d+e）。于是有如下结论：

定理2系统（4）在平衡点E1处是稳定的，如果R1＜0，否则系统（4）是不稳定的，这里

3.3 E2（x2，y2，0）的稳定性

设J2为系统在平衡点E2处的Jacobian 矩阵，则

因此有如下结论：

定理3系统（4）在平衡点E2处是稳定的，如果R2＜0 且满足下列条件

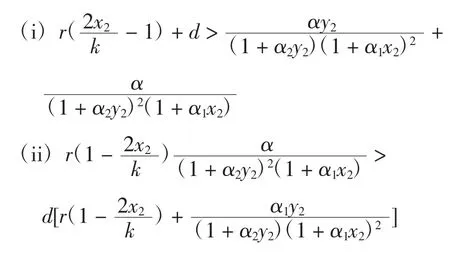
4 E*（x*，y*，z*）附近的系统动力学行为

4.1 局部稳定性

系统在内部平衡点E*（x*，y*，z*）附近的Jacobian矩阵为

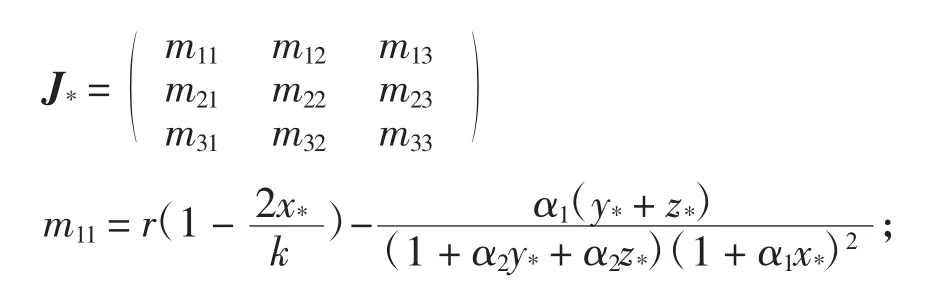
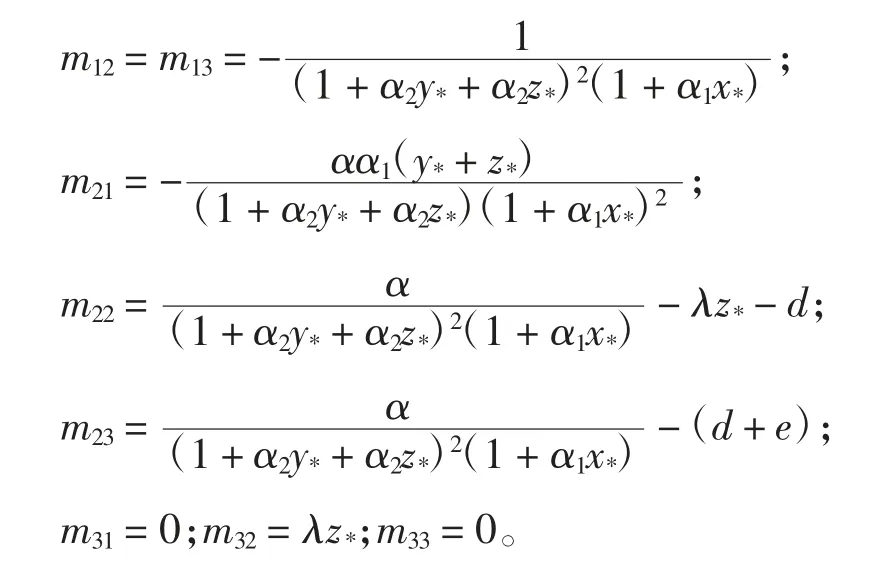
J*的特征方程为

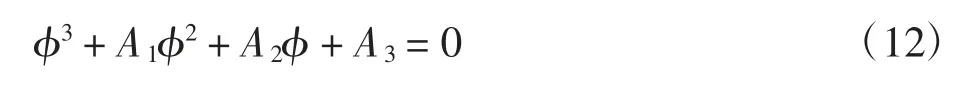
式中：A1=-m11-m22；A2=m11m22-m12m21-m23m32；A3=m23m32m11-m13m32m21；A1A2-A3=-m112m22-m222m11+m11m12m21+m22m12m21+m22m23m32+m32m13m21。

假设m11+m22＜0，m23m11＞m13m21，m12m21＞m22m11，m22m23＞0，因而有A1＞0，A3＞0，A1A2-A3＞0。根据Routh-Hurwitz 准则，内部平衡点E*是局部渐近稳定的。

4.2 全局稳定性

定理4当B1＞0，B2＞0，B3＞0 时，内部平衡点E*（x*，y*，z*）是全局渐近稳定的，其中B1、B2、B3见后面定义。

证明定义正定Lyapunov 函数

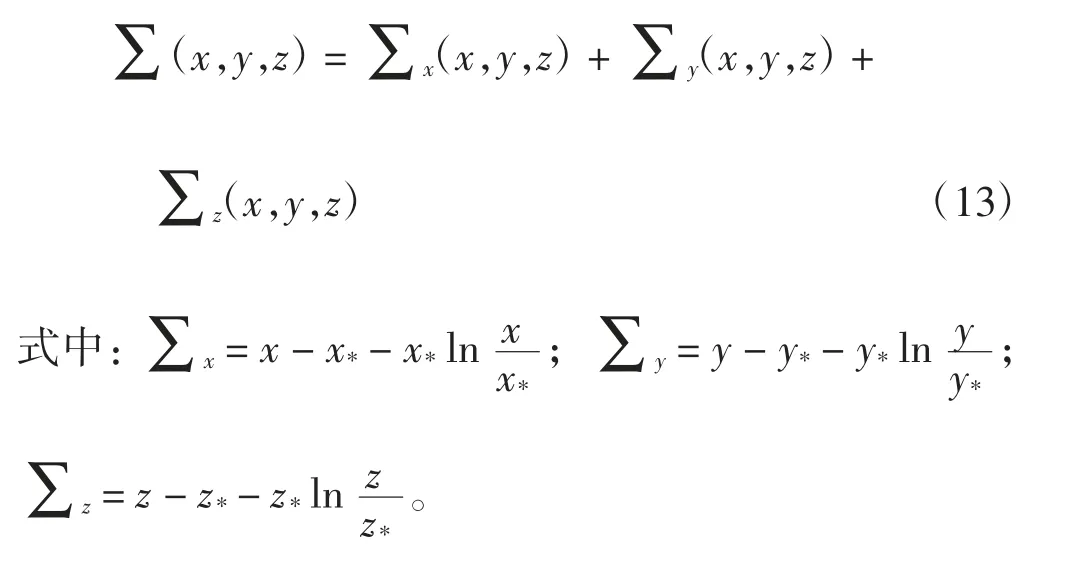
计算Σx沿系统（4）的解的关于时间的导数，得到

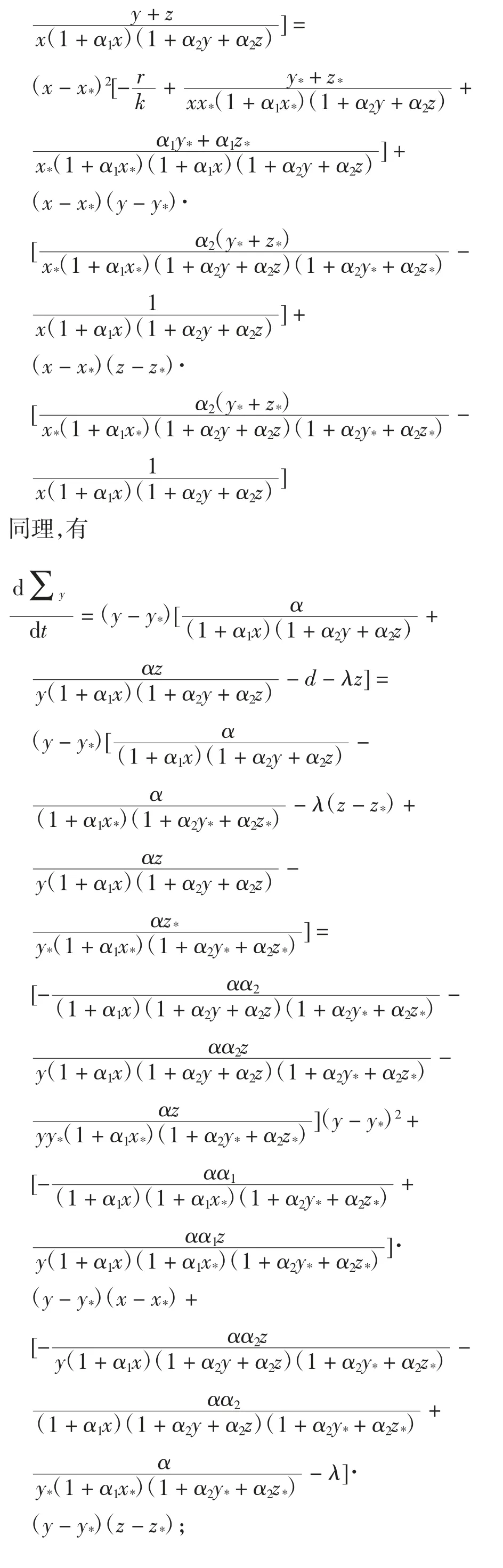
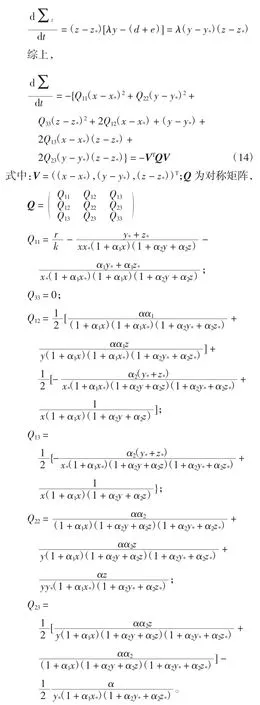
若对称矩阵Q 的所有主子式均为正，即

则内部平衡点E*（x*，y*，z*）是全局渐近稳定的。

5 持久性

定理5若

则系统（4）是持久的。

证明使用平均Lyapunov 函数的方法[10]

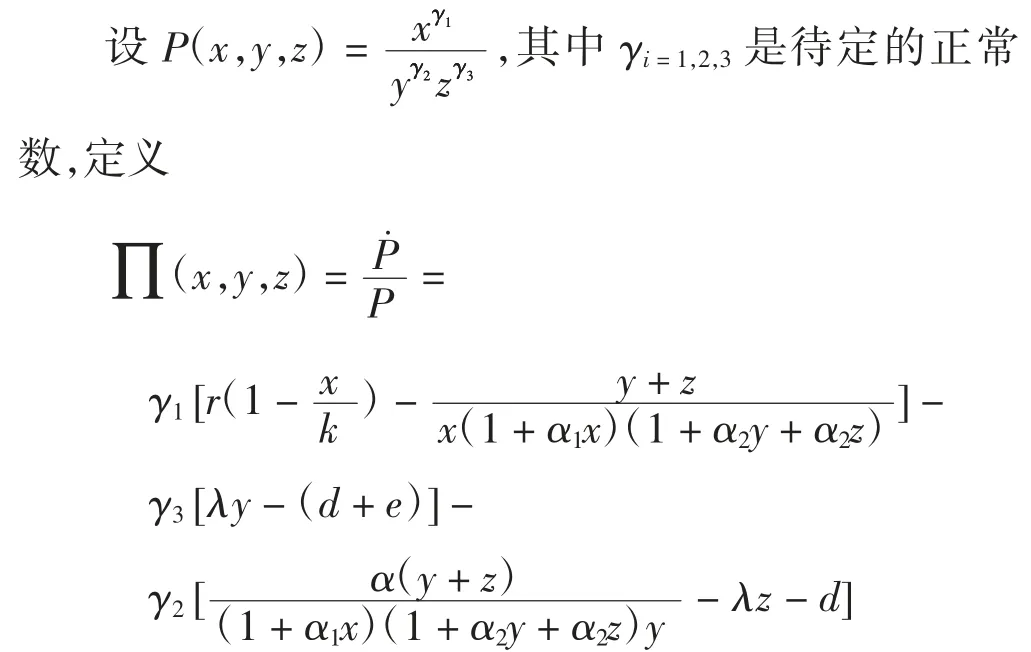
欲证明该函数在每个边界平衡处都为正，首先有

根据条件（i）、条件（ii）和条件（iii），得

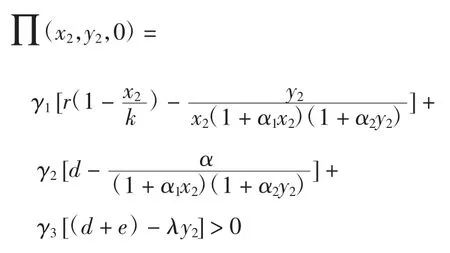
选择适当的γi=1，2，3，确保在边界平衡处∏＞0，因此系统（4）是持久的。

6 数值模拟

利用Matlab-R2014a 对模型进行数值模拟，并使用标准的Matlab 微分方程积分器进行Runge-kutta 方法验证。要验证模型的分析结果，本文选择一组生物上可行的假设参数值：r=0.4，k=60.0，α1=0.2，α2=0.3，α=0.4，λ=0.004，d=0.02，e=0.01。除了验证本文得到的结果外，从现实角度看，这些数据模拟也是非常重要的。

模拟系统（4）在满足初始条件x0=50，y0=40，z0=80 时围绕内部平衡点E*处的稳定性行为，解关于时间序列的演化情况如图1 所示。

图1 解关于时间序列的演化情况

由图1 可知，在没有同类相食的情况下，所有物种都以振荡的方式共存。但由于同类相食的存在，所有物种都因振荡行为而维持在一个稳定的位置。

模拟系统（4）在满足初始条件x0=50，y0=40，z0=80 时，围绕内部平衡点E*处的稳定性行为，模型的相图如图2 所示。

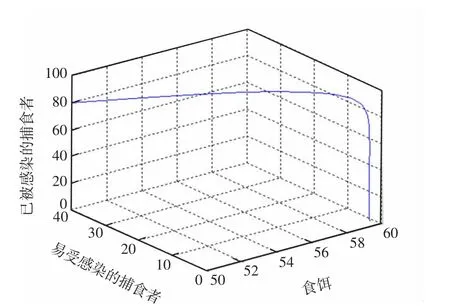
图2 模型的相图

由图2 可知，系统在内部平衡点E*上是稳定的，即从正区域E∈R3+开始的轨线都收敛到E*。根据上述假设参数值，验证得到A1＞0，A3＞0，A1A2-A3＞0，B1＞0，B2＞0，B3＞0。因此，图2 显示系统在内部平衡点E*处是全局稳定的，这意味着该疾病可以侵入系统并达到流行水平。

7 结语

本文考虑的是具有Bazykin 型功能反应函数的捕食者-食饵模型，由于考虑到疾病的因素，文章将传统的二维模型变为三维进行分析，将捕食者种群分为2类，分别是易受感染的捕食者和已经被感染的捕食者，尝试研究三维的捕食者-食饵模型。并对所建三维模型的有界性、平衡点的存在性以及可行平衡点的局部稳定性和全局稳定性进行分析。本文首先证明了系统的有界性和平衡点的存在性，得到系统共有4 个平衡点，分别为平凡平衡点E0、轴向平衡点E1、平面平衡点E2和内部平衡点E*。其次根据Hurwitz 判据、Lyapunov 函数构造等方法对模型的稳定性进行分析，得到平凡平衡点E0是不稳定的，在满足特定的条件下，轴向平衡点E1、平面平衡点E2和内部平衡点E*是渐近稳定的，同时内部平衡点E*也是全局稳定的。最后得出结论，带有被感染的捕食者的生态流行性捕食者-食饵模型展现出非常有趣的动态。本文中考虑的是具有Bazykin 型功能反应函数的模型，今后可以考虑更多种功能反应类型的机制，还可以考虑加入一些时滞行为使模型更加贴近现实。