初相位及其求解方法

赵保现

近几年全国高考理综物理试卷中,相继出现了与质点振动方程有关的题目．笔者发现,求解这类问题时,遇到的难点往往是如何正确计算初相位,为此,本文结合具体实例,介绍一种求解初相位的方法．

1 初相位概念

图1为某列简谐波的图象,对波上任一质点而言,质点离开平衡位置的位移y跟时刻t的关系均可写为如下形式:

y=Asin(ωt+φ). (也可用余弦函数表示)

(※)

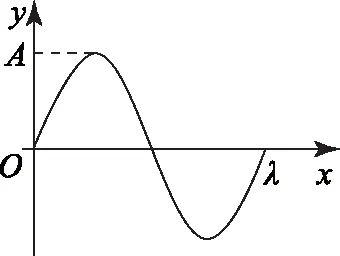
图1

(※)式叫作质点的振动方程,其图象称为质点的振动图象．若T为波的周期,则

令θ=ωt+φ,则θ称为相位,不难看出: 1)t=0时,相位θ的值等于φ,φ称为初相位,所以初相位就是t=0时的相位．解决具体问题时,可灵活选取计时起点(即t=0的时刻)．2) 初相位φ的取值范围为0≤φ≤2π或-π≤φ≤π．

2 初相位的求解方法

1) 将已知的某一具体时刻t0、该时刻质点的位移y0以及振幅A、角频率ω或周期T,代入(※)式,一般情况下可求出0≤φ≤2π或-π≤φ≤π范围内φ的2个不同值φ1、φ2．

2) 参考(※)式,写出质点的振动方程(这时方程中A、ω或T、φ1或φ2为已知量,y和t为未知量),再应用数学三角函数图象的作图方法,画出两个对应的振动图象.某时刻哪个图象表示的质点振动方向与波上对应质点、对应时刻的振动方向一致,哪个图象对应的φ值就是所求的初相位．

特例:若求出的φ只有一个值,则该值就是初相位．

3 应用举例

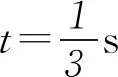
(ⅰ)波速及波的传播方向;

(ⅱ)质点Q的平衡位置的x坐标．

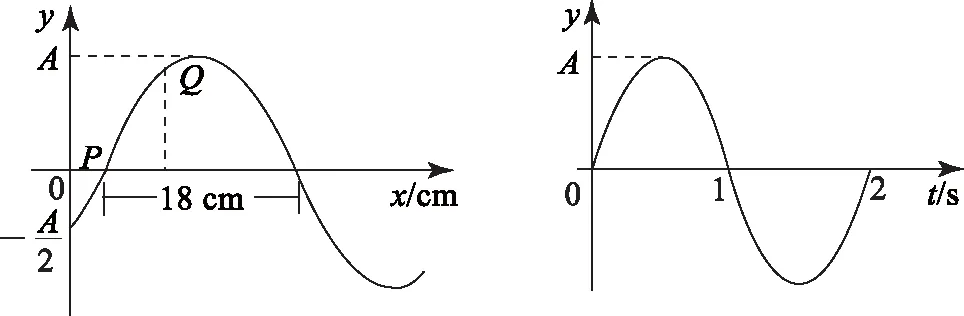
图2 图3

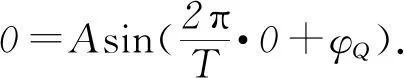
①

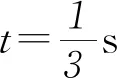
②

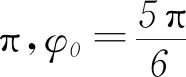
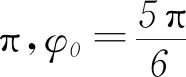
y=Asin(πt+π)=-Asin πt

和

或

画出对应的振动图象,分别如图4、图5、图6、图7所示．

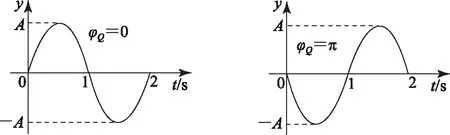
图4 图5

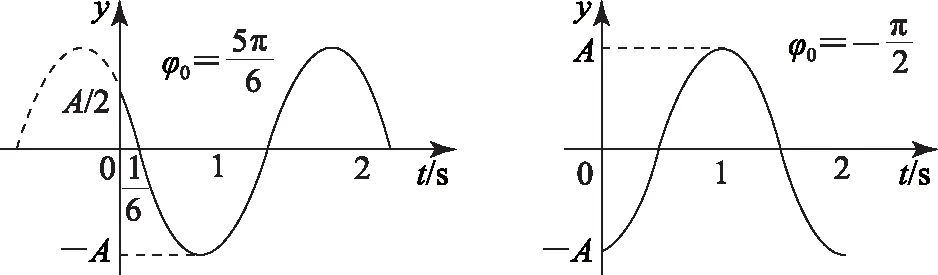
图6 图7

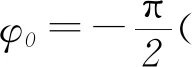
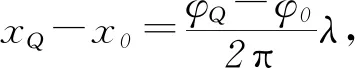
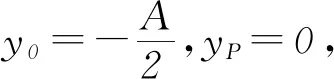
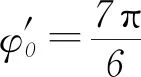
对应的振动图象分别如图8、图9、图10、图11所示．

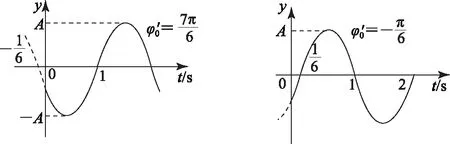
图8 图9

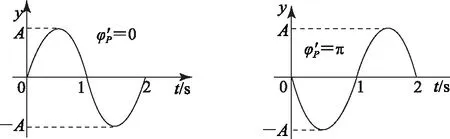
图10 图11

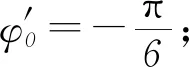
由此可见,规定的计时起点不同,同一质点(例如x=0处的质点)振动的初相位就可能不同．

链接练习

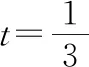
(ⅰ)简谐波的周期、波速和波长;

(ⅱ)质点O的位移随时间变化的关系式．

2.(2014年全国卷Ⅱ)图12为一列简谐横波在t=0.10 s时刻的波形图,P是平衡位置在x=1.0 m处的质点,Q是平衡位置在x=4.0 m处的质点;图13为质点Q的振动图象．下列说法正确的是________．

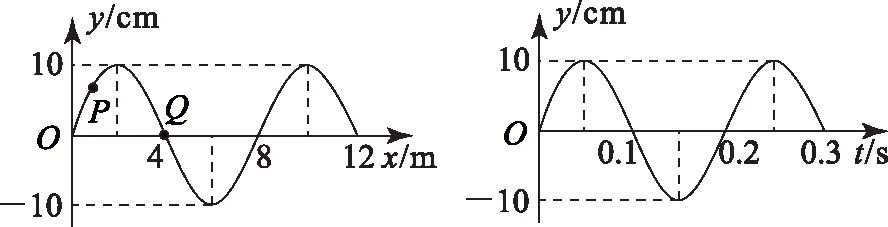
图12 图13

A. 在t=0.10 s时,质点Q向y轴正方向运动

B. 在t=0.25 s时,质点P的加速度方向与y轴正方向相同

C. 从t=0.10 s到t=0.25 s,该波沿x轴负方向传播了6 m

D. 从t=0.10 s到t=0.25 s,质点P通过的路程为30 cm

E. 质点Q简谐运动的表达式为y=0.01sin 10πt(国际单位制)

链接练习参考答案

1. (ⅰ)周期为4 s,波速为7.5 m·s-1,波长为30 cm．

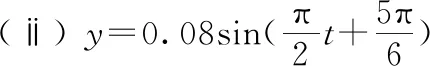
2. B、C、E．