用对应思想解排列组合题

王荣峰(特级教师)

所谓对应思想就是在两个事物之间建立起来的一种关系,即对应关系,从而揭示事物之间的联系,它是解决数学问题的一种基本思想和策略.本文就对应思想在解排列组合题中的主要应用进行盘点,以期能对大家解题能力的提升有所帮助.

1 元素分配问题

例1全集U={1,2,3,4,5,6,7},集合A,B都是U的子集,若A∩B={2,4,6},则称A,B为“理想配集”,记作(A,B),这样的“理想配集”共有( )个.

A. 15 B. 16

C. 81 D. 82

解析 如图1所示，分别用两个椭圆的内部表示集合A与B，因为A∩B={2,4,6}，所以2,4,6必须选择区域Ⅱ;对于1,3,5,7,每个数都可选择Ⅰ,Ⅲ,Ⅳ3个区域中的任意1个,由分步计数原理知，共有3×3×3×3=81种不同的选择方式,且每一种选择方式都有唯一对应的一个集合对(A,B),即相应的集合对(A,B)共有81对. 选C.

图1

点评 该题并不复杂,挖掘“理想配集”的定义,借助分步计数原理先计算出自由元素1,3,5,7有多少种分配方式,然后再进行合理对应,问题便可获解,即先分步,再对应.

2 共点方格问题

例2在m×n(m,n≥3,m,n∈N*)的棋盘上取两个小方格,若这两个小方格恰有一个公共点,则不同的取法共有( )种.

A.mn

B. 2mn

C. (m-1)(n-1)

D. 2(m-1)(n-1)

图2

解析 从图2可以看出,每个公共点P都对应两种不同的取法,即取两个黑格或两个白格.由于在m×n的棋盘内部的m-1条横线与n-1条竖线共对应了(m-1)·(n-1)个交点,所以满足条件的取法共有2(m-1)·(n-1)种. 选D.

点评 注意到每个公共点P都对应两种不同的取法,进而可将问题等价转化为求棋盘内横竖线对应的交点问题,从而找到问题解决的切入点,即先对应,再对应.

3 最短路径问题

例3如图3,坐标平面内有一质点P从原点O出发,目标是点M(5,4),若质点P每次只能沿坐标轴移动1个单位,则它到达目标点M的最短路径共有( )条.

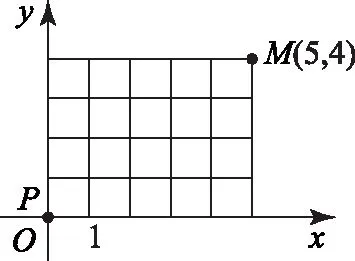
图3

A. 9 B. 20

C. 126 D. 1 024

点评 弄清质点P从O到M的“最短路径”是怎样构成的,是借助对应思想用排列组合知识破解该题的前提条件,即先对应,再排列.

4 异面直线问题

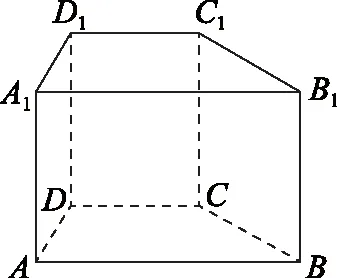
图4

例4如图4所示,底面是梯形的直四棱柱ABCD-A1B1C1D1的8个顶点可确定28条直线，在这些直线中,异面直线共有( )对.

A. 174 B. 180

C. 186 D. 192

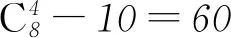
点评 在用1个四面体去对应3对异面直线时,为了确保转化是等价的,必须要先检视题目中不能出现三点或多点共线的情况,即先检视,再对应.

5 等差数列问题

例5已知数列{an}为等差数列,从集合A={a1,a2,…,a20}中取出3个不同的数,使这3个数成等差数列,则不同的等差数列共有( )个.

A. 90 B. 120 C. 180 D. 200

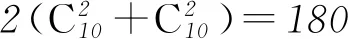
点评 由2j=i+k发现只要i+k为偶数便可确定唯一的j,进而先将集合A分成角标为奇数和角标为偶数两类,再巧妙对应,即先分类,再对应.

6 不定方程问题

例6不定方程3x1+x2+…+x10=4 ①共有( )组非负整数解.

A. 9 B. 373 C. 495 D. 504

解析 当x1=1时,方程①变为x2+x3+…+x10=1,显然有9组解;

当x1=0时,方程①变为x2+x3+…+x10=4,即(x2+1)+(x3+1)+…+(x10+1)=13,令xi+1=yi,则yi≥1(2≤i≤10),上式可等价化为y2+y3+…+y10=13. ②

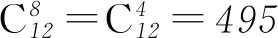
综上所述，方程①的非负整数解共有504组. 选D.

点评 通过在xi(2≤i≤10)上加上1实现了非负整数解到正整数解的转化,再用“隔板法”进行巧妙对应从而找到问题解决的突破口,即先转化,再对应.

7 条件传球问题

例7甲、乙、丙、丁、戊5个人站成一圈玩传球游戏,每次只能传给相邻的两个人,从甲开始传,若第10次球又传回到甲的手里,则共有( )种不同的传球方式.

A. 252 B. 254

C. 512 D. 1 024

解析 不妨设逆时针传一次球为“+”,顺时针传一次球为“-”，则分两种情况:

1)逆时针传两圈或顺时针传两圈均可传回到甲手中,有2种可能;

综上所述，总的传球方式有254种. 选B.

点评 处理该题很容易忽视对情况1)的讨论,传球次数是奇数还是偶数,是否是5的倍数等都制约着不同的对应方式,即先讨论,再对应.

8 有序数组问题

例8已知A={1,2,3,…,14,15},B={a1,a2,a3},则同时满足:①BA;②a2-a1≥3;a3-a2≥4的集合B有( )个.

A. 30 B. 56

C. 120 D. 364

点评 该题难度比较大,可以应用我们所熟知的“隔板法”来求解,但不如上述先插空,再排序,然后对应的解法，上述解法独辟蹊径,解题过程令人耳目一新,即先插空,再对应.

9 可重组合问题

例9从集合A={1,2,3,…,n}中取出r个数组成一组(a1,a2,…,ar),若满足:① 数字允许重复出现;② 不计数字的顺序,则称(a1,a2,…,ar)为集合A的一个“r可重组合”,这样的“r可重组合”共有( )个.

点评 解该题的难点是用0,1,2,…,r-1逐个加到ai(1≤i≤r)上进行铺垫,进而实现了从“可重组合”到“无重复组合”的一一对应,然后再从集合B中选取r个元素就可顺利解答该题,即先对应,再选取.

10 围棋比赛问题

例10甲、乙两个围棋队各5名队员按事先排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰,然后负方的2号队员再与对方的获胜队员比赛,负者又被淘汰,一直这样进行下去,直到有一方队员全被淘汰时,另一方获胜,形成了一种比赛过程,那么所有可能出现的过程共有( )种.

A. 252 B. 126 C. 70 D. 35

点评 解本题的常规思路是按照比赛分5,6,7,8,9局进行讨论,但先利用排列建立模型,再用对应思想进行转化达到了增加思维量、减少计算量的目的,即先建模,再对应.

对应作为一种数学思想和方法，对处理较难的排列组合问题有着十分广泛的应用.用该方法解题的关键在于构造对应关系,但此法没有通法可寻,只有平时勤于积累,善于总结,才能依据具体问题的特征进行分析，进而合理对应,最终使问题顺利获解.