反馈对儿童早期数学学习效果的影响元分析

吕 雪，郭力平，李姗姗

反馈对儿童早期数学学习效果的影响元分析

吕 雪1，2，郭力平1，2，李姗姗1

（1．华东师范大学 教育学部，上海 200062； 2．华东师范大学 中国基础教育质量监测协同创新中心华东师大分中心，上海 200062）

反馈被认为是促进学生学习的最有力方式，信息技术的发展为反馈设计提供了支持．采用元分析方法考察反馈对儿童早期数学学习的影响，研究发现：反馈对儿童早期数学学习有较小的积极效果．通过调节分析发现，任务类型和反馈类型对反馈效果具有调节作用，反馈媒介、反馈时机和反馈效果测量时间对反馈效果无调节作用．未来关于反馈对儿童早期数学学习效果影响的研究，应在教育信息化背景下从任务特征、学习者特点和反馈特征3个方面综合考虑，提高反馈的针对性和个性化．

反馈；数学学习；元分析；儿童；信息技术

1 引言

在学习环境中，反馈通常被定义为提供给学习者的关于个体表现或理解情况的信息[1]．学习者可以通过反馈确认、添加、改写、调整或重组记忆中的信息，无论这些信息是领域知识、元认知知识、关于自我和任务的信念，还是认知策略[2]．反馈是广泛使用的教学行为，如课堂上的点评与追问、作业的评语、测试成绩的书面报告或口头分析等，都涉及反馈．引人注意的是当前在形成性评价和个性化学习背景下专门探究反馈对学习效果影响的研究越来越多．

已有文献对反馈做了划分．Shute将反馈分为3类：正误型反馈（knowledge of results，KR）、正确答案反馈（knowledge of correct response，KCR）和解释型反馈（elaborated feedback，EF）[3]．这为更细致地研究反馈对学习的影响提供了方向．KR只提供关于结果正确与否的信息，不提供正确答案；KCR可能直接提供正确答案或者给予正误信息之后提供正确答案；解释型反馈通常涉及正确答案，解释为什么回答是错误或正确的．还有一种策略型反馈不提供结果方面的信息，根据被试的解题策略提供反馈信息．一些具体的研究发现反馈对于数学学习的正向作用[4-5]．尽管有这些正向的结论，研究也强调反馈效果存在相当大的变动性[6]，这种变动性表明反馈的影响常常取决于任务和学习者的特性．从反馈中学习的效果通常依赖于个体整合长时记忆中已有知识和反馈中新信息的能力[1]．虽然先前的知识通常有益，但它也可能产生消极后果．在一些少数案例中，有反馈相较于无反馈可能产生中性或者负向的效果[7]．对于掌握充足的领域知识的个体而言，正误性反馈可能导致已经建立的知识结构和反馈之间的认知冲突，从而影响个体表现[8]．

反馈被认为是促进学生学习的重要方式[9]．然而，近一个世纪的反馈研究表明反馈对学习效果的影响具有很大变动性[7]，个体学习者对于不同情境中不同类型反馈的回应是不同的．个性化反馈可能是增进学习效果的关键，基于学习者特点的个性化的反馈更可能增进学习成效[10]．随着信息技术的不断发展，基于计算机技术的反馈设计越来越广泛，并应用于学生的学习过程支持与学习评价．现有研究表明数字化反馈的效果同样也依赖于学习者的特征[11]．

已有的反馈对学习效果影响的元分析缺少对某一学科领域或某一年龄段儿童学习效果的具体分析，很多综合概括化的结果具体到某一领域或某一特定年龄儿童时，结果的可应用性不强[9，12]．对于特定的学习领域而言，数学学科具有很强的逻辑性和系统性，在学习过程中更加需要适时的反馈．以往针对中学生数学学习效果的反馈研究已经证实了反馈的积极作用[13-14]．此外，技术中介的反馈对儿童早期学习效果的影响以及如何产生效果的比较研究也缺少梳理．反馈对儿童早期数学学习效果的研究成果尚较为零散，还缺少综合系统的量化分析．因此，探究反馈对儿童早期数学学习效果的整体作用及相应影响因素至关重要．

借助信息技术的数字化反馈研究中，小学与学前阶段儿童未得到充分关注．迄今只有少数研究探讨了小学阶段数字化反馈对学习的影响．由于管理工作记忆效能的脑区还在发展变化中[15]，儿童早期对反馈的处理与成人不同[16]，因此，反馈文献尤其是一般性元分析结果是否能推广到这个年龄组值得商榷．综上，反馈对学习的影响存在很大变动性．反馈作用的发挥与反馈类型、学习者特征、学习情境、学习结果水平均有关系，基于目前的研究现状，关注反馈对儿童早期数学学习的具体影响和作用机制具有实践指导意义．

2 研究方法

2.1 文献检索与筛选

2018年10月至12月，通过国内外相关数据库进行检索，外文数据库使用Science Direct、EBSCO（含ASP、BSP、PsycInfo、PsycArticle、ERIC、Ebooks等）、Web of Science、Taylor & Francis Online进行检索，由于已有研究中对儿童早期关注较少，因此检索暂未限定年龄和学段，检索主题词为：（1）feedback，（2）math/reasoning/problem solving，上述检索词以“AND”组合．中文文献主要以中国知网、万方数据库、台湾华艺数据库进行搜索．由于关于反馈研究的中文文献较少，故检索词设定范围宽泛，检索词为：（1）反馈，（2）学习，两类检索词以“AND”组合．文献初步筛选标准为：（1）研究内容为反馈对儿童学习的影响；（2）文献能够提供定量的数据结果；（3）发表时间、国家地区不限；（4）文献来源为期刊、学位论文和会议论文；（5）文章用英文或中文发表．

2.2 纳入标准

根据检索词进行一次检索，再根据一次检索获得文献的参考文献进行回溯和二次检索，经过初步筛选，共得到中文文献7篇，外文文献78篇．依据研究目的及操作性定义，确定纳入标准如下：（1）研究反馈对儿童数学学习的影响；（2）研究为实验或准实验设计，包括反馈组和非反馈组；（3）参与被试包括小学中低年级或幼儿园阶段发展正常儿童，平均年龄上限为8岁左右．由于相关研究数量较少，研究并未报告单一年龄段儿童数据结果，因此以平均年龄作为年龄限制标准；（4）研究结果能够计算出效应值；（5）样本量不低于10人；（6）国家和地区不限．最终筛选出外文文献9篇，中文文献1篇．

2.3 文献编码

为了便于进行统计分析，对纳入元分析的10项研究进行特征值编码，编码的内容包括作者、发表时间、文献来源、样本来源（被试所属国家）、样本量、平均年龄、反馈介质（包括计算机反馈和个人反馈）、反馈类型（包括正误型反馈、正确答案反馈、策略型反馈等）、反馈时间（包括及时反馈和延时反馈）、反馈效果测试时间（包括及时效果和延时效果）、研究领域（包括数学等式推理、类比推理、数学天平问题解决等）．研究由两位研究者在同一时间段内对全部文献进行编码，编码结果的一致性为92%．

编码结果显示：纳入研究10项，均为期刊论文，其中有期刊论文和学位论文数据相同情况，因此将学位论文排除．部分论文中有多组实验设计，故有多个效应值，共计26个．样本总量为2 531人，最小样本量为37人，最大样本量为613人．样本来源分布为中国3项、美国6项、荷兰1项，详见表1．

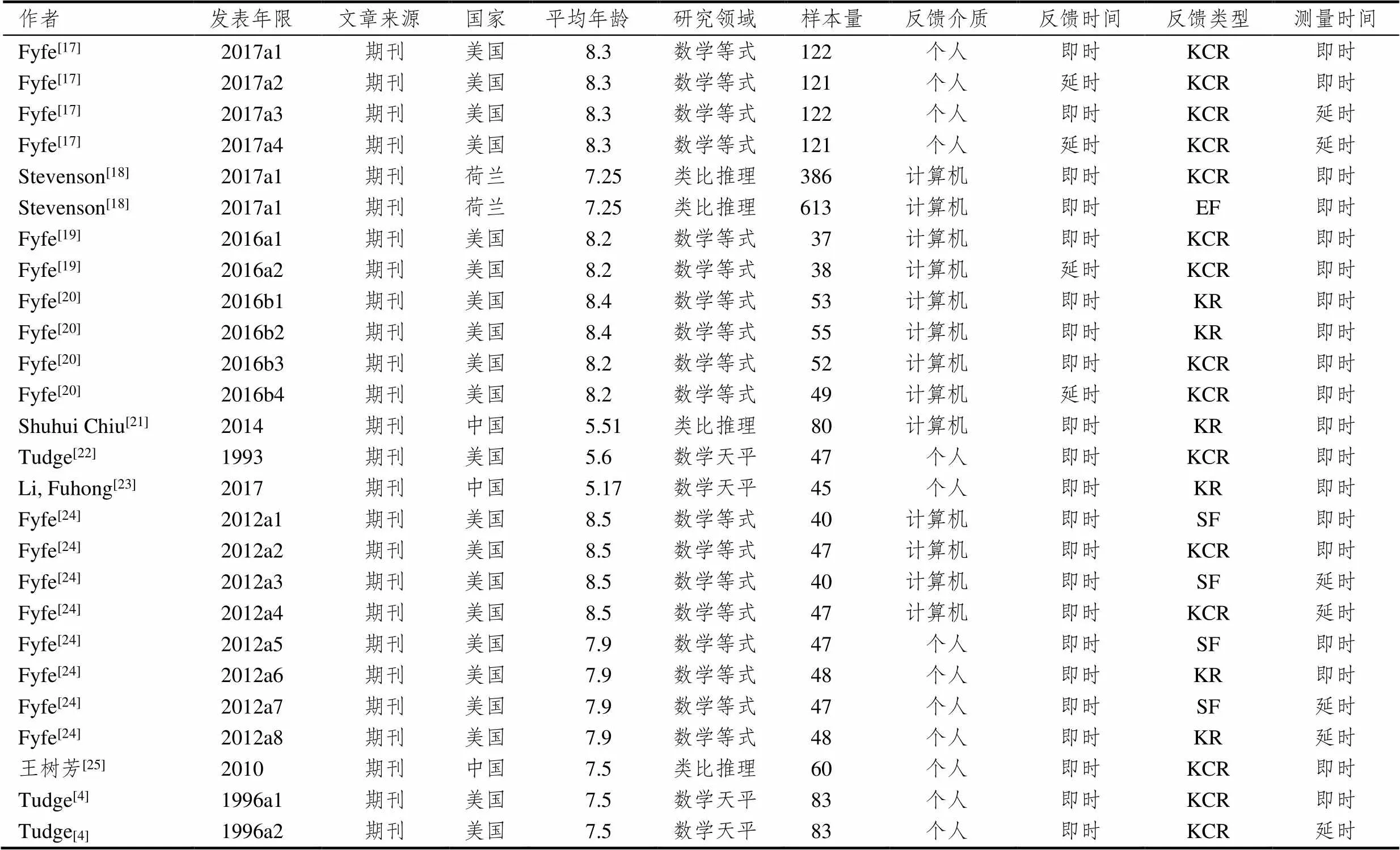
表1 纳入文献主要信息表

注：2012a1表示同一篇研究的第一组效应值，其它类推．KR表示正误反馈，KCR表示正确答案反馈，SF表示策略型反馈，EF表示详细解释型反馈．

2.4 元分析程序

元分析运用Comprehensive Meta-Analysis Version 2.0 （CMA-V2.0）统计软件进行数据处理．采用反馈组和无反馈组的测验分数的均值差作为效应值．由于不同研究实验或准实验设计不同，测查工具不同，因此采用标准化的均值差和Hedges’g作为效应值．由于半数左右的实验研究或准实验研究的样本量比较小，Hedges’g作为效应值更合适，发表偏倚更小一些，因此选择Hedges’g作为最终的效应值．在具体的效应值计算过程中，如果一个研究中有两个不同设计的反馈组与同一个无反馈组组进行对比，那么为了避免样本的重复计算，将无反馈组的被试量分半计算．单个样本进行了不同测试的情况下，取平均效应值作为此样本的效应值．

3 研究结果分析

3.1 效应值分布和异质性检验

研究基于Hedges’g值呈现的漏斗图分析文献的发表偏倚情况．从图1可以看出，效应值大部分分布在漏斗的中上部，且较为均匀地分布在中线两侧，可以判定出现发表偏倚的可能性较小．通过Begg’s的秩相关法（=0.659）和Egger’s回归法（=0.32）对发表偏倚进行检验，值均大于0.5，未发现发表偏倚．从异质性检验结果来看，Q统计显示各效应值是异质的，=152.241，2=83.79，<0.001，表明83.6%的变异是由效应值的真实差异造成的，因此研究采用考虑了研究内和研究间变异的随机效应模型，效应值的置信区间（）为95%．

图1 反馈对儿童早期数学学习效果影响的效应值分布

3.2 反馈对儿童早期数学学习效果的整体影响

反馈对儿童数学学习效果的整体结果如图2森林图所示，采用随机效应模型的数据结果，共包含10个研究样本，26项效应值，总体效应值=0.236，且达到统计显著水平（<0.05）．根据Cohen的效应值统计标准，效应值在0.2左右，被认为影响较小，效应值为0.5左右，认定为中等程度影响，效应值在0.8左右，被视为影响很大，效果显著[26]．由此可见，相比于无反馈信息，反馈对儿童数学学习有较小优势．在26项效应值中，正向效应值为19个，占比为73.1%，其中9项达到显著水平；负向效应值为7个，占比为26.9%，其中2项达到显著水平．

3.3 任务类型和反馈特征对反馈效果的调节作用

在异质性检验中发现，研究结果之间存在异质性，出现异质性可能因为具体研究任务、反馈特征不同所导致，因此将从上述两个方面进行调节分析，了解反馈对儿童早期数学学习效果的具体差异．

3.3.1 任务类型对反馈效果的影响

纳入元分析的10项研究中数学任务情境有所不同，根据学习内容抽象程度大致可以分为抽象符号类任务和具体形象类任务，抽象符号类任务主要是数学等式推理，具体形象类任务主要为图形类比推理和数学天平问题．不同抽象程度的任务情境下，反馈对学习效果的调节分析结果见表2，反馈对抽象符号类数学任务产生负向影响，但合并效应值极小（-0.027），且未达到统计显著水平（>0.05）；反馈对具体形象类任务存在正向作用，合并效应值为0.752，为中等程度的影响，且达到统计显著水平（<0.001）．从组间效应检验结果来看，反馈对不同类型数学任务的学习效果影响存在显著性差异，=25.689，<0.001．结果表明，反馈对具体形象类数学任务的学习更为有利．

3.3.2 反馈特征对反馈学习效果的调节分析

（1）反馈媒介对反馈效果的调节分析．

已有研究中，儿童数学学习的反馈媒介主要有计算机和个人．不同反馈媒介下的反馈效果详见表3，计算机作为媒介对反馈效果有正向作用，合并效应值为0.162，但未达到统计显著性（>0.05）；个人反馈对数学学习产生正向影响，合并效应值为0.308，且达到显著性水平（<0.05）．通过调节分析发现，计算机和个人两种反馈媒介对反馈效果没有调节作用，=0.546，>0.05．

个人反馈的效应值略大于计算机反馈的效应值，可能与任务类型有关，计算机作为反馈媒介的13个样本中任务类型均为抽象符号类任务．个人反馈的13个样本中具体和抽象类任务均有．通过对个人反馈的13个样本进行二次元分析，以任务类型为调节变量，发现反馈对具体形象类任务产生了积极影响，合并效应值为0.892，达到统计显著水平（<0.01），而反馈对抽象符号类任务存在负向作用，合并效应值为-0.015，但未达到统计显著水平（>0.05），组间效应检验发现任务类型对反馈效果存在调节作用，=8.899，<0.01，因此可以推断个人反馈的效应值略大于计算机反馈的效应值与任务类型有关，与反馈媒介自身的影响不大．

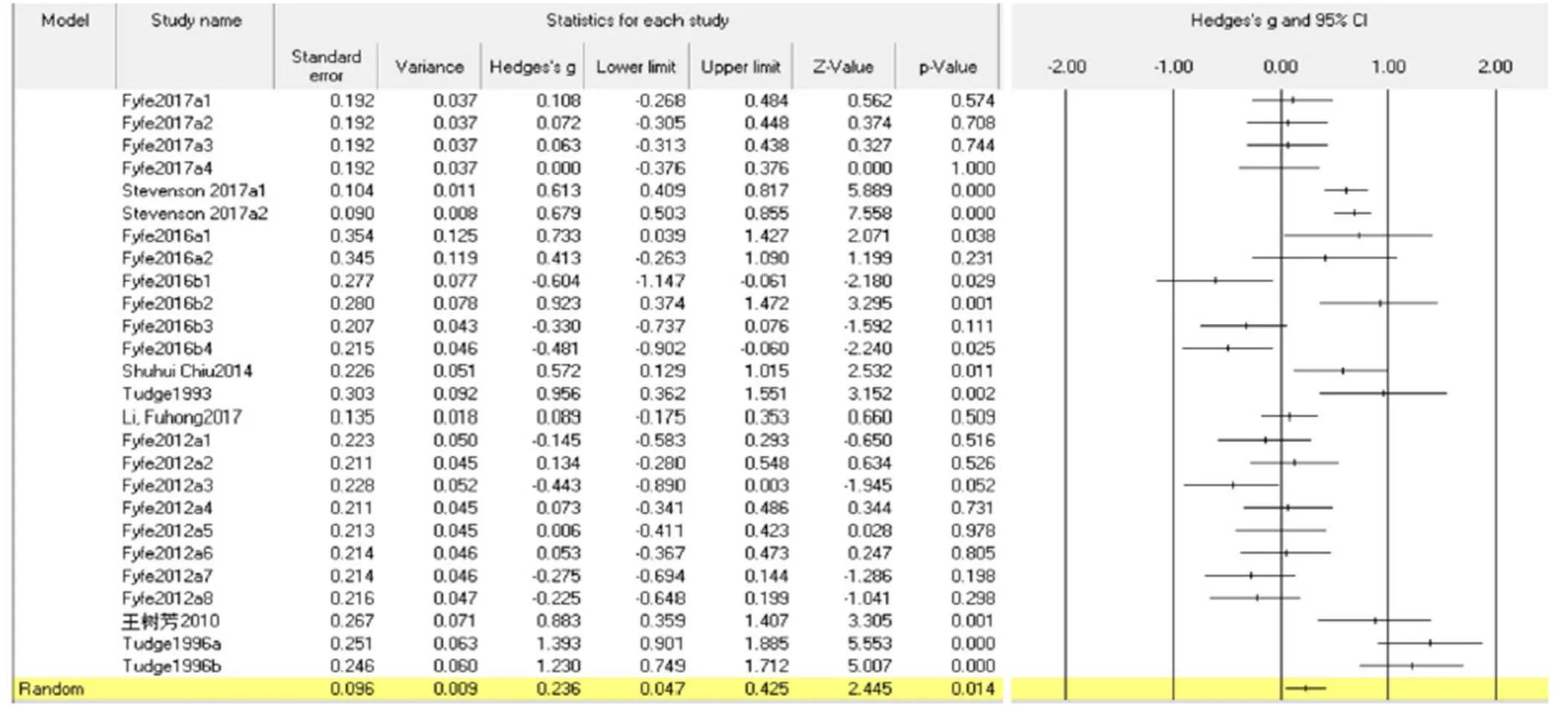
图2 反馈元分析具体结果

（2）反馈类型对反馈效果的调节分析．

对纳入元分析的研究中的反馈类型进行编码，发现主要包括正误型反馈（knowledge of results，KR），正确答案反馈（knowledge of correct response，KCR）、策略型反馈和解释型反馈．由于解释型反馈仅有一项，无法达到统计学意义，故在反馈类型的调节分析中排除．反馈类型对反馈效果的影响见表3，由表3可知，KR对数学学习有正向作用，合并效应值分别为0.13，未达到统计显著水平（>0.05），KCR对数学学习的积极影响更大，合并效应值为0.367，且达到统计显著水平（<0.01）．而策略型反馈对数学学习存在消极影响，合并效应值为-0.208，未达到统计显著性（>0.05）．组间效应检验发现，不同反馈类型对反馈效果存在显著调节作用，=11.339，<0.01．

（3）反馈时机对反馈效果的调节分析．

反馈时机分为即时反馈和延时反馈，即时反馈和延时反馈是相对而言，一般情况下，即时反馈是针对项目的反馈，即一道题目完成后即给予反馈；延时反馈是在所有题目作答完毕后给予反馈信息．纳入元分析的研究均是上述描述的即时与延时反馈．通过调节分析发现，即时反馈对儿童数学学习为正向影响，合并效应值为0.282，达到显著水平（<0.01），说明即时反馈对儿童早期数学学习产生较小的积极影响．而延时反馈对儿童数学学习产生负向作用，合并效应值为-0.043，但未达到显著水平（>0.05）．组间效应检验结果见表3，反馈时机对反馈效果不存在调节作用，=2.793，>0.05．

（4）反馈效果测量时间对反馈效果的调节分析．

目前研究中主要通过反馈干预后的后测分数来检验反馈的效果．根据反馈效果的测量时间可以分为即时效果和延时效果，反馈的即时效果指反馈干预后即进行测验，延时效果指反馈干预结束一段时间后进行测验，不同研究中间隔的时间不同．经过统计分析发现，反馈对数学学习的即时效果产生积极作用（详见表3），合并效应值为0.305，达到统计显著水平（<0.01）．反馈对数学学习的延时效果产生正向作用，但效应值极小，合并效应值为0.052，且未达到统计显著水平（>0.05）．组间效应检验发现，不同时间测量的反馈效果无显著性差异，=1.378，>0.05．

表2 反馈对不同类型数学任务学习效果的影响

注：***表示值达到0.001显著水平，**表示值达到0.01显著水平，*表示值达到0. 05显著水平，以下同．

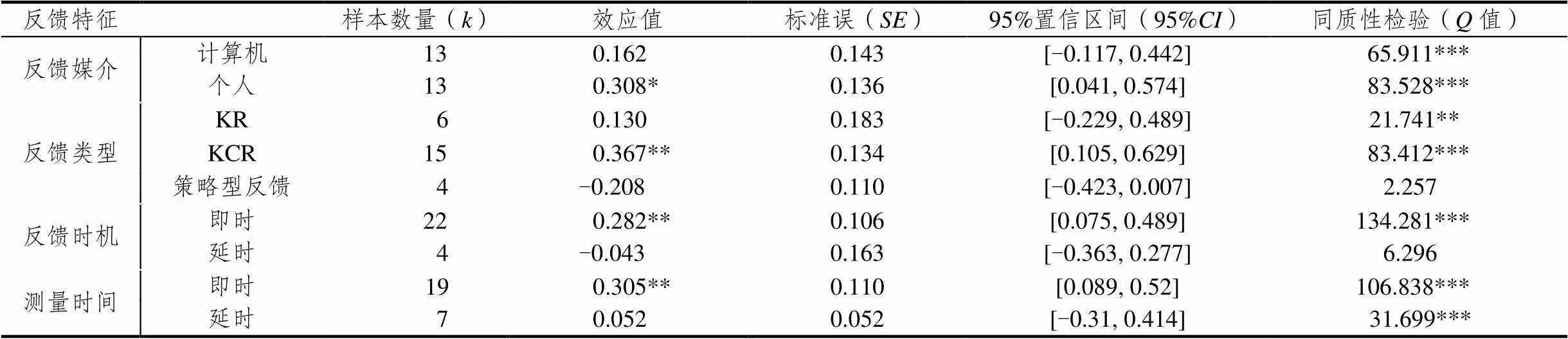
表3 不同反馈特征对反馈效果的影响

4 讨论

4.1 反馈对儿童早期数学学习效果的整体影响

通过统计分析发现，反馈对儿童早期数学学习有较小的积极效果，需要注意的是反馈效果在不同的研究间具有较大差异，这与Hattie和Gan的研究一致[6]．一些研究中反馈对数学学习无作用或者存在消极效果，说明未来需要进一步了解学习者处理反馈信息的认知过程以及学习者的先验知识水平对反馈效果的影响[27]．

4.2 任务类型和反馈特征对儿童早期数学学习效果的调节作用

4.2.1 学习任务类型对反馈效果的影响

反馈作用的正负方向及影响强度与数学学习任务类型、反馈特征、学习者认知发展水平均有关系．反馈对具体形象型任务的学习更为有利．这一结果与儿童的思维特点以及认知加工能力有关．儿童早期思维发展处于前运算阶段，需要借助具体事物或图像进行认知加工．抽象符号型任务解决过程本身就需要更多的认知资源，调动更多的知识和技能，从而影响对反馈信息的注意和加工．学习者的特征（现有知识水平、动机水平、元认知技能、情感状态、工作记忆容量等）对反馈效果有重要影响[10]，是进一步探究反馈对儿童早期数学学习影响的关键因素．此外，需要注意的是抽象性任务的研究均来自同一研究团队，未来需要进一步验证反馈对抽象符号型任务的影响．

4.2.2 反馈媒介对反馈效果的影响

随着信息技术的不断发展及其在教育领域的广泛应用，人们看到了基于计算机进行个性化学习和评价的可能性和优势．例如计算机自适应测验的开发与应用，同样，基于计算机技术，学生可以得到一对一的即时或延时反馈，更具操作性、个性化和有针对性．反馈媒介对反馈效果没有调节作用，可以看出，经过科学设计的技术媒介的反馈能够达到和个人反馈相同的效果，为未来提高反馈的效率和针对性奠定了基础．同时，研究者也看到计算机媒介的正向作用并未达到统计显著水平，说明数字化的反馈设计更专业化还有很长的路要走．目前的反馈设计较多基于行为主义的模式，提供相对简单的强化和简单的被试反应与反馈联结，而儿童学习经验的建构比较复杂和充满个性化，需要在反馈设计过程中更好地尊重儿童的学习特点，结合新的多元媒介反馈形式深入研究，以提供灵活个性化的反馈．

4.2.3 反馈类型对数学学习效果的影响

反馈类型对反馈效果存在显著调节作用．事实上，不同类型的反馈指向的反馈水平也存在差异．KR和KCR是基于任务水平的反馈，策略型反馈是指向认知过程的反馈．由于KR自身能够提供的信息比较有限，被试无法获得更多改进信息，因此KR的效应值略小于KCR的效应值，这与Van der Kleij等人的研究结果一致[12]．需要强调的是已有研究的任务形式并不复杂，任务本身并未涉及连续不断的探究过程，探究空间不大，在此种任务情境中，KCR的效应值略大于KR的效应值，而在开放性探究性任务情境中，反馈的作用还未可知．策略型反馈的消极影响虽然未达到统计显著性，但由于目前样本量较小，仍需要进一步探究．至于策略型反馈对学习效果没有产生正向作用，可能是儿童一方面需要认知资源解决问题，给出答案，一方面需要对策略型反馈进行编码加工，导致认知负荷过重或者认知加工过程偏离目标．此外，对于策略的反馈，需要儿童进行回顾和反思，对于儿童早期的挑战更大．至于解释型反馈对儿童早期数学学习的作用，已有研究还很少，是可以探究的方向．

4.2.4 反馈时机对数学学习效果的影响

反馈时机对反馈效果不存在调节作用，但即时反馈对儿童早期数学学习产生积极影响，且达到统计显著水平．综合而言，关于即时和延时反馈对学习效果的研究结论并不一致，存在很大变异性．Kulhavy和Anderson的干扰持续假说主要关注反馈在个体错误纠正中的作用[28]．该假说指出延时反馈呈现的信息能够使个体更有效地进行错误纠正，而跟随不正确反应后的即时反馈是无效的，因为在记忆中不正确的反应干扰了对反馈提供的正确答案的编码．需要强调的是这一假说更多用于解释陈述性材料和低水平学习结果的延时反馈积极效果．也有研究者认为即时反馈的效果更好，越早提供纠正性信息，信息结果越可能有效保留[29]．即时反馈提供关于学习目标和进程的信息，有利于维持学习动机，提高自我效能感[30]．Corbett和Anderson近二十年的编程和数学指导中成功使用了即时反馈[31]．

有研究者提出根据任务难度（相对于学习者当前能力水平）选择反馈时间，即时反馈对低能力的学习者或困难的任务更有效，延迟反馈对高能力学习者或相对容易的任务更有效[32]．纳入元分析的研究任务均属于数学问题解决，是较高水平的学习任务，即时反馈产生了积极作用．此外，在本元分析中，即时反馈产生正向作用，与儿童早期的记忆特点有关，儿童早期记忆容量有限，保持时间短，而延时反馈提供的信息量较大，儿童在加工反馈信息的同时，还需要回忆对任务的先前反应．

在反馈效果方面，反馈的即时效果和延时效果无差异，说明反馈学习是循环式和递推式，它的作用可能仅限于同一个循环内．为了更好地发挥反馈的作用，需要持续地提供有针对性的反馈．此外，受儿童早期认知发展特点影响，对反馈信息的长时间保持和再现较为困难，这也说明提供持续过程性反馈具有重要意义．

5 结论与启示

元分析结果发现，反馈对儿童早期数学学习产生较小的积极作用，合并效应值为0.36，且达到统计显著水平（<0.05）．进一步分析发现，任务类型对反馈效果有调节作用，反馈对具体形象类任务的学习效果更为积极．不同反馈类型的反馈效果存在显著差异，相较而言，KCR的效应值大于KR和策略型反馈的效应值；即时反馈对数学学习有较小的正向作用，反馈对学习的即时正向效果显著，反馈媒介对学习效果无调节作用．

由此可见，反馈对儿童早期数学学习整体效果有一定优势，但具体分析反馈作用时，需要综合考虑任务特征、反馈特征及学习者特点．为更好地了解反馈作用机制，发挥反馈的正向影响，关于反馈对儿童早期数学学习影响的研究可以从以下几方面进一步探究．

5.1 反馈对儿童早期数学学习效果的影响需要考虑任务类型和学习者特征

目前的研究中数学学习的任务主要是问题解决，涉及到知识和技能的迁移和应用，属于高水平学习结果，那么反馈对低水平数学学习任务（主要涉及知识的识记、再现或再认）的影响还需探究．对于学龄前儿童而言，数学学习是非正式的数学学习，更加强调数学兴趣和好奇心的激发，注重学习探索的过程，而不只是简单的数学知识和技能的获得．在更为开放的数学学习情境中，反馈类型对反馈效果的影响需要进一步研究．此外，反馈设计中还要考虑学习者的特点，学习者在学习方式、元认知技能、动机和情感状态、学习策略和学习风格等方面存在着差异．诸多个体因素可能影响学习者对反馈信息的处理和加工，因此在后续研究中需要考虑学习者特征对反馈效果的影响．

5.2 反馈特征的设计应综合考虑

通过元分析的结果，可以知道反馈媒介、反馈类型等反馈特征对反馈效果的影响，但不同反馈特征之间的交叉影响尚不清楚．Hattie和Timperley将反馈归为4种水平：自我的反馈、任务的反馈、过程的反馈以及调节的反馈[9]．研究主要关注的是任务的反馈对儿童早期数学学习的影响．其它反馈水平对儿童早期数学学习的影响需进一步探究．反馈积极效果的实现需要综合考虑反馈特征和学习者特征，而且学习过程应该是自主的，尊重儿童学习的自主性是有效连接反馈特征和学习者特征的桥梁．儿童不应只是被动处理反馈信息，而应能够适当自主选择是否需要反馈，什么时候需要反馈，需要什么类型和水平的反馈．

5.3 数学学习需要持续动态的个性化反馈

教育部颁发的《教育信息化十年发展规划（2011—2020年）》首次提出“信息技术与教育深度融合”[33]．在当今的教育情境中，技术的融入为教育个性化提供了更多可能．传统基于计算机的反馈设计往往只提供相同的任务和固定的反馈，随着自适应技术的发展，可以在自适应情境中提供反馈，即根据儿童能力水平，单个题目作答情况提供相应的反馈，反馈更加有针对性[34-35]．反馈的提供可以更为多样，一方面可以在同一任务中根据儿童反应给予或儿童自主选择不同特征或水平的反馈，另一方面，可以利用信息技术，提供综合多种媒介的反馈[36-37]．同时，也要思考技术的应用如何与儿童生活的真实世界有机联系，而非割裂儿童与现实生活世界的互动．

[1] MORY E H. Feedback research revisited [M] // JONASSEN D. Handbook of research on educational communications and technology. Mahwah: Lawrence Erlbaum, 2004: 745-783.

[2] WINNE P H, BUTLER D L. Student cognition in learning from teaching [J]. International Encyclopedia of Education, 1994 (2): 5 738-5 775.

[3] SHUTE V J. Focus on formative feedback [J]. Review of Educational Research, 2008, 78 (1): 153-189.

[4] TUDGE J R H, WINTERHOFF P A, HOGAN D M. The cognitive consequences of collaborative problem solving with and without feedback [J]. Child Development, 1996, 67 (6): 2 892-2 909.

[5] CORBALAN G, PAAS F, CUYPERS H. Computer-based feedback in linear algebra: Effects on transfer performance and motivation [J]. Computers & Education, 2010, 55 (2): 692-703.

[6] HATTIE J, GAN M. Instruction based on feedback [M] // ALEXANDER P, MAYER R E. Handbook of research on learning and instruction. New York: Rout ledge, 2011: 249-271.

[7] KLUGER A N, DENISI A. The effects of feedback interventions on performance: A historical review, a meta-analysis, and a preliminary feedback intervention theory [J]. Psychological Bulletin, 1996, 119 (2): 254.

[8] NIHALANI P K, MAYRATH M, ROBINSON D H. When feedback harms and collaboration helps in computer simulation environments: An expertise reversal effect [J]. Journal of Educational Psychology, 2011, 103 (4): 776.

[9] HATTIE J, TIMPERLEY H. The power of feedback [J]. Review of Educational Research, 2007, 77 (1): 81-112.

[10]  NARCISS S, SOSNOVSKY S, SCHNAUBERT L, et al. Exploring feedback and student characteristics relevant for personalizing feedback strategies [J]. Computers & Education, 2014 (71): 56-76.

[11]  NARCISS S. The impact of informative tutoring feedback and self-efficacy on motivation and achievement in concept learning [J]. Experimental Psychology, 2004, 51 (3): 214-228.

[12] VAN DER KLEIJ F M, FESKENS R C W, EGGEN T J H M. Effects of feedback in a computer-based learning environment on students’ learning outcomes: A meta-analysis [J]. Review of Educational Research, 2015, 85 (4): 475-511.

[13] AJOGBEJE O J, OJO A A, OJO O A. Effect of formative testing with feedback on students’ achievement in junior secondary school mathematics inOndo State Nigeria [J]. International Education Research, 2013, 1 (2): 8-20.

[14] JAMES A O, FOLORUNSO A M. Effect of feedback and remediation on students’ achievement in junior secondary school mathematics [J]. International Education Studies, 2012, 5 (5): 153.

[15]  VAN DUIJVENVOORDE A C K, ZANOLIE K, ROMBOUTS S A R B, et al. Evaluating the negative or valuing the positive? Neural mechanisms supporting feedback-based learning across development [J]. Journal of Neuroscience, 2008, 28 (38): 9 495-9 503.

[16]  EPPINGER B, MOCK B, KRAY J. Developmental differences in learning and error processing: Evidence from ERPS [J]. Psychophysiology, 2009, 46 (5): 1 043-1 053.

[17]  FYFE E R, RITTLE-JOHNSON B. Mathematics practice without feedback: A desirable difficulty in a classroom setting [J]. Instructional Science, 2017, 45 (2): 177-194.

[18]  STEVENSON C E. Role of working memory and strategy-use in feedback effects on children’s progression in analogy solving: An explanatory item response theory account [J]. International Journal of Artificial Intelligence in Education, 2017, 27 (3): 393-418.

[19]  FYFE E R, RITTLE-JOHNSON B. The benefits of computer-generated feedback for mathematics problem solving [J]. Journal of Experimental Child Psychology, 2016 (147): 140-151.

[20]  FYFE E R, RITTLE-JOHNSON B. Feedback both helps and hinders learning: The causal role of prior knowledge [J]. Journal of Educational Psychology, 2016, 108 (1): 82.

[21]  CHIU S, ALEXANDER P A. Young children’s analogical reasoning: The role of immediate feedback [J]. Journal of Psycho-educational Assessment, 2014, 32 (5): 417-428.

[22]  TUDGE J R H, WINTERHOFF P A. Can young children benefit from collaborative problem solving? Tracing the effects of partner competence and feedback [J]. Social Development, 1993, 2 (3): 242-259.

[23]  LI F, XIE L, YANG X, et al. The effect of feedback and operational experience on children’s rule learning [J]. Frontiers in Psychology, 2017 (8): 534.

[24]  FYFE E R, RITTLE-JOHNSON B, DECARO M S. The effects of feedback during exploratory mathematics problem solving: Prior knowledge matters [J]. Journal of Educational Psychology, 2012, 104 (4): 1 094.

[25] 王树芳，莫雷，金花．任务难度和反馈学习对儿童类比推理能力的影响[J]．心理发展与教育，2010，26（1）：24-30．

[26]  COHEN J, COHEN J, COHEN J W, et al. Statistical power analysis for the behavioral science [J]. Techno-metrics, 1988, 31 (4): 499-500.

[27] TIMMS M, DEVELLE S, LAY D. Towards a model of how learners process feedback: A deeper look at learning [J]. Australian Journal of Education, 2016 (60): 128-145.

[28] KULHAVY R W, ANDERSON R C. Delay-retention effect with multiple-choice tests [J]. Journal of Educational Psychology, 1972, 63 (5): 505.

[29]  PHYE G D, ANDRE T. Delayed retention effect: Attention, perseverance, or both? [J]. Contemporary Educational Psychology, 1989, 14 (2): 173-185.

[30]  SCHUNK D H. Self-efficacy for reading and writing: Influence of modeling, goal setting, and self-evaluation [J]. Reading & Writing Quarterly, 2003, 19 (2): 159-172.

[31]  CORBETT A T, ANDERSON J R. Locus of feedback control in computer-based tutoring: Impact on learning rate, achievement and attitudes [C] // Proceedings of the SIGCHI conference on Human factors in computing systems. ACM, 2001: 245-252.

[32]  BANGERT-DROWNS R L, KULIK C L C, KULIK J A, et al. The instructional effect of feedback in test-like events [J]. Review of Educational Research, 1991, 61 (2): 213-238.

[33] 教育部．教育信息化十年发展规划（2011—2020年）[EB/OL]．（2012-03-13）[2018-04-21]．http://www.moe.gov.cn/ srcsite/A16/s3342/201203/t20120313_133322.html.

[34]  SHUTE V J, ZAPATA-RIVERA D. Adaptive technologies [M] // JONASSEN D, SPECTOR M J, DRISCOLL M, et al. Handbook of research on educational communications and technology: A project of the association for educational communications and technology. Mahwah: Lawrence Erlbaum, 2008: 277-294.

[35]  NARCISS S. Feedback strategies for interactive learning tasks [M] // JONASSEN D, SPECTOR M J, DRISCOLL M, et al. Handbook of research on educational communications and technology: A project of the association for educational communications and technology. Mahwah: Lawrence Erlbaum, 2008: 125-144.

[36]  NARCISS S, HUTH K. Fostering achievement and motivation with bug-related tutoring feedback in a computer-based training for written subtraction [J]. Learning and Instruction, 2006, 16 (4): 310-322.

[37]  XU M. An investigation of the effectiveness of intelligent elaborative feedback afforded by pedagogical agents on improving young Chinese language learners’ vocabulary acquisition [D]. Illinois: Northern Illinois University, 2009: 2-5.

Effects of Feedback on Young Children’s Mathematics Learning Outcomes: A Meta-Analysis

LV Xue1, 2, GUO Li-ping1, 2, LI Shan-shan1

( 1. Department of Preschool Education, Faculty of Education, East China Normal University, Shanghai 200062, China; 2. Center of Assessment towards Basic Education Quality, East China Normal University, Shanghai 200062, China)

Feedback was viewed as one of the most powerful means to increase student learning. Meanwhile the development of information technology provided support for feedback design. Given the current state of research, there was a need for a meta-analysis focusing on specific aspects of young children. The present meta-analysis was conducted on the effects of feedback on young children’s mathematics learning. A small but significant additional benefit of feedback was found for mathematics learning whose overall effect size was 0.236 based on data from 2 531children in 10 studies. Moderator analyses were performed using a random effects model to contrast sub-samples based on different categorical study variables. It was found that the task type of Mathematics and feedback type were significant moderator of the effect sizes. However, the effects of feedback on mathematics learning with different feedback media, feedback time and feedback effect retention time were more consistent. In the future, the study of the effect of feedback on young children’s mathematical learning should be taken into consideration in three aspects: task characteristics, learners’ characteristics and feedback characteristics in the context of educational information, so as to improve the pertinence and individualization of the feedback.

feedback; mathematics learning; meta-analysis; young children; information technology

2019-09-27

教育部人文社会科学研究规划基金项目——物联网背景下儿童在游戏中学习的评价研究（17YJAZH026）；受“中国基础教育质量监测协同创新中心华东师范大学分中心”资助

吕雪（1987—），女，黑龙江大庆人，博士生，主要从事学前教育评价、学前儿童认知发展与教育研究．郭力平为本文通讯作者．

G610

A

1004-9894（2020）01-0086-07

吕雪，郭力平，李姗姗．反馈对儿童早期数学学习效果的影响元分析[J]．数学教育学报，2020，29（1）：86-92．

[责任编校：陈隽、张楠]