几何机器明证引发的思考

张景中，彭翕成，邹 宇

几何机器明证引发的思考

张景中1，2，彭翕成1，邹 宇2

（1．华中师范大学 国家数字化学习工程技术研究中心，湖北 武汉 430079；2．广州大学计算科技研究院，广东 广州 510006）

时代发展要求教育资源智能化，而不是简单的“电子化”．智能解答能在教育领域得以应用的基本要求是能被人理解接受，即有很好的可读性．最新研究表明，人类的解答未必是最好的，计算机可能给出让人惊讶的解答．计算机给出的解答甚至比题干还短，这看似“有悖”常识，但又引起思考，如何知识表示才能尽量简洁而又方便推理．知识的创新表示，要尽量符合信息时代的要求，同时也可能造成原有知识体系的重新定位．

人工智能；教育应用；几何定理；机器明证；知识表示和推理

1 教育智能化是时代发展的必然要求

2016年AlphaGo横空出世，击败了人类围棋世界冠军，人机博弈举世瞩目，言必称“人工智能”的时代已经到来[1-4]．人工智能研究包含但不限于以下研究课题：自然语言理解、数据库的智能检索、专家咨询系统、博弈、机器人学、自动程序设计、定理证明等．这里研究的几何定理机器证明属于定理证明领域的分支，包括如何让计算机自动出题以及解答．

解题研究是数学教学中的重要组成部分．学习数学离不开解题．学生要通过解题练习来掌握数学知识，老师需要通过试题分析来帮助学生提高．师生们面对各种难题，不会做怎么办？考试出题人压力更大，总被要求出题要有新意．一年当中，考试繁多，对题目需求量大，那么多的新题从何而来？

这些问题存在多年．对于出题人而言，虽绞尽脑汁创新，但由于受到习惯思维的约束，与已有试题“撞车”也是常事．与之相对的是，广大师生（甚至包括家长）为解不出题，又找不到答案而苦恼．因此近十年来，各种题库网站（包括APP）如雨后春笋般冒出，如菁优网、魔方格、猿题库、学霸君、作业帮等，颇受欢迎．其中智能手机的普及和拍照搜题技术的发展在其中起了很大的推动作用．只是题库再大，毕竟有限．对题库中没有的题目，就无能为力了．所以，在线题库相对纸质版的题典，只是题量更大，搜索更便捷．在智能化方面，并没有本质提升．缺少智能性或智能化程度不高是现有教学资源的一大通病[5-6]．

因此，利用计算机来研究智能化地命题和解题，很有现实意义．计算机出题，可不受已有题目的干扰，容易创新．如同AlphaGo下棋，很多招法超出人的想象．计算机解题，则可与已有题库网站形成互补．题库网站主要解决题库已有题目，而计算机解题系统可解决题库中没有的题目．对于题库已有题目，计算机解答系统也可以生成解答，对照检验，看原有解答是否正确，又可给学习者提供多种解答思路．这也为接下来的自动批改打下基础．

目前从宏观上讨论人工智能与教育应用的文章已经很多了，这里将分享作者最近从事几何定理机器证明的一些思考．

2 机器证明可读性是教育应用的基本要求

人工智能发展几十年，发表了海量的学术论文．发展到一定阶段，需要总结思考．在一些学术会议上，有人提出：人从小学到中学，读书12年，到了18岁成年时，要通过高考，那么目前的计算机能否通过高考？这需要通过实践来检验．

中国在2015年启动了一个有关类人答题的863项目，其中包括初等数学的类人答题，要求计算机给出能被高考阅卷人认可的解答，解答所使用的方法和知识点必须在中小学课标范围之内．2017年6月7日，国产高考机器人挑战北京卷文科数学以及全国二卷文科数学的考试，分别用时22分钟和10分钟，得分为105分和100分．这是一个相当不错的成绩．这一成绩的取得，与中国科研工作者长期的努力是分不开的．

1959年，IBM公司的Gelernter（曾参加1956年的达特茅斯会议）等人提出了后推搜索法来解几何题，这一研究是20世纪50年代人工智能领域代表性成果之一，大大激发了人们对定理机器证明的兴趣，确立了其在人工智能研究领域中的重要地位．但直到1976年，机器解答几何题还停留在很初级的阶段，只能解决一些很简单的问题．

1977年，由于吴文俊先生创造性的工作，几何定理机器证明取得了突破性进展．吴方法能判定几何命题的真假，但其推理常涉及多达数百项甚至上千项的多项式计算，过程繁琐，人们难以理解这些多项式的几何意义，或者说证明的可读性不令人满意，检验起来困难．从学术上来说，吴方法在理论上立得住，实践中也有章可循，甚至有些简单问题手算都可以完成．但从教育应用而言，可读性差严重影响推广普及．

以吴方法为代表的代数方法大获成功，人们自然希望乘胜追击，对机器证明提出了更高的要求．在之后多次有关机器证明的国际学术会议上，都有人提出这样的问题：能不能由计算机给出易于理解、易于检验的证明，即所谓可读的证明？

定理的证明应该被同行检验，这是学术惯例．当年四色问题的机器证明不可读，引发了一场哲学讨论：什么才算一个数学证明？一般认为是，立足于一系列公理，从概念、定义、已有定理出发，采用演绎推理，得到新的结论．证明一方面要说服自己，当解答者理清思路，认识从模糊到清晰，才可能得出一个推理正确的证明．证明同时也要说服他人．所以一个好的证明除了推理正确，简洁明了也很重要．毕竟其他人未必有足够的时间和兴趣来检验你的证明．因此有观点认为[7]，证明就是某一特定时间，被某一特殊群体接受的解释．Thomas Tymoczko认为[8]，数学证明应该有说服力（convincing）、可检验（surveyable）、形式化（formalizable）．用数学同行公认的语言进行表达，是为同行检验提供基础；而检验的目的则是为了说服同行，得到学术共同体的认可．如果证明不可检验，形式化的工作白做，也不可能说服同行，因此可检验非常重要[9]．

是否“易于理解、检验”，是一个模糊概念，因人而异．数学水平高、知识面丰富的，当然理解能力强．对于教育应用而言，必须假定读者对象为中学师生．

机器能否生成可读证明？数理逻辑专家王浩先生认为，机器证明本质是用量的复杂来代替质的困难．吴文俊先生进一步指出，人作几何题，可根据不同情形找寻不同的巧法，巧则巧矣，却是一题一法；机器证明要用统一算法解决不同问题，解题过程不可能简捷．机器证明是用冗繁但有章可循的计算来代替简捷巧妙但法无定法的推演．

尽管已有权威的论断，但仍然有研究者没有放弃．1992年，张景中等[10]提出了面积消点法，实现了“可读证明（readable proof）”．在当时看来，人能读懂的机器证明，是极好的了，能与人工证明媲美了．

叶征等[11]认为，几何定理常有图形辅助，阅读证明时需反复比对证明文本和文本所对图形中的几何元素．如判定三角形全等，首先要在图形中找到这两个三角形，然后判定这两个三角形是否大致全等，之后再继续．当证明较长，或几何图形变复杂，不管是人工证明，还是机器证明，即使所谓的可读证明也会变得不易阅读和理解．因此提出几何定理可视证明（visually proof），希望采用计算机图形动画等方式帮助理解，使得几何证明变得直观．实践表明，这是一种有效的方式．

问题是，当证明很长时，即便每一步都有几何意义，即便每一步都有动画辅助，读者依然会感到吃力，难以坚持读下去．可见，可视证明有助于读者理解证明，但治标不治本．扬汤止沸，不如釜底抽薪．只有改善证明本身，使其变得简短易懂，才可能根本解决．

杨路等[12]在攻克不等式机器证明这一难题时，提出了“明证（certificate）”这一目标，即证明一旦给出，读者无需太多专业知识，很容易就能判断证明是否正确，甚至是一目了然的．明证都无需专家审稿，普通读者就能检验．

一个不等式，一旦写成平方和的形式，其结论一目了然．那么，几何问题能否也实现“明证”，一行搞定？

一方面来说，几何问题实现明证，要比不等式容易．因为不等式涉及“高次”，且变量多．几何题虽有时也涉及“高次”，但多数情况下是一次、二次；几何题虽从未限定过点、线、圆的个数，但多数情况下个数都不太多．但从另外角度来说，几何题要实现明证，又要比不等式难得多．因为不等式（这里主要指代数不等式）本身就是代数关系式，具备转化变形的基础．而几何题涉及的几何关系，需要通过转换成代数形式，才有可能列出希望的“一行等式”．也就是几何题比不等式多了一道转化手续．解析几何虽能实现几何、代数之间的转化，但表示几何关系和表示几何关系之间的关系十分繁琐．因此有必要研究新的几何表示，使得能简洁明了表示几何关系；又要找到一种比较简单的方法，将几何关系之间连接起来．

3 信息时代促使知识表示的再创造

一个知识点，往往存在多种表述形式．知识在传递给学生的时候，很有必要进行批判再加工．这里的批判，主要不是怀疑这些知识的正确性，而是检查它在教育上的适用性．要用系统科学的观点，联系前后左右的教学，联系学生的心理特征与年龄特征，看一看，问一问，哪种反映方式较优？能不能找到更优或最优的反映方式．

学习几何，可选欧氏几何，或解析几何，或向量几何，或质点几何，甚至可以创造新的几何体系．哪种方案能更快更好地完成这一阶段数学教育的任务呢？这需要仔细考察．在信息时代，还需要考虑该体系是否能被计算机简单地形式化处理．

以中点为例加以说明．怎么表示点是线段的中点？方法很多．

文字描述：点是线段的中点．

图形描述（图1）：

图1

欧氏几何描述：=．但不要漏掉：、、共线，否则只能说明点在线段的中垂线上．

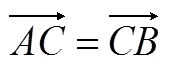
中位线定理：

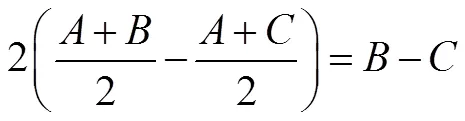
重心定理：

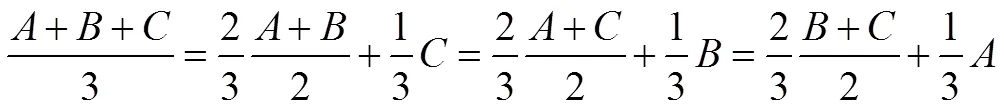
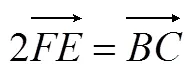
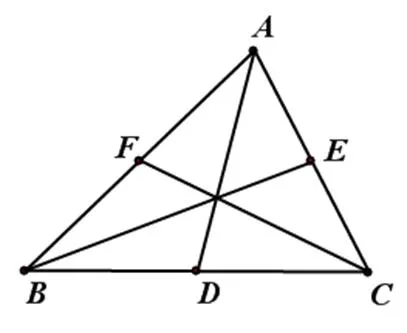
图2

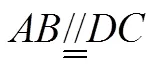
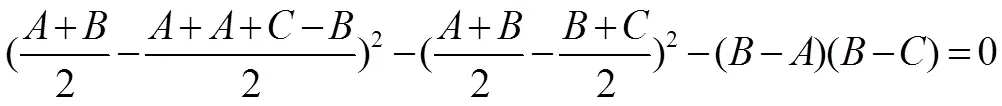
四边形是平行四边形的充要条件是：

．

等式简单变形，能得到新的几何性质，说明这一体系易于扩展，生成新的知识．就是从这样平凡之处着手，建立了点几何体系[13-18]，并实现了多种基于点几何的自动推理算法，其中以点几何恒等式算法尤为漂亮．

从知识工程[19]的角度来看，知识获取和知识表示是从人类已有的知识源进行抽取总结，并转化成形式化的知识，便于用于问题求解．所谓形式化，是指利用计算机能接受并进行处理的符号和方式来表示人类知识．符号表示是指用符号和符号结构来表示各种概念和概念之间的关系．知识表示的选择应满足：① 充分表达领域知识；② 有利于运用知识进行推理，有利于提高搜索速度及推理效率；③ 便于知识的维护和管理；④ 便于理解和实现．

建构一种新的几何体系，虽是为教育的目的，但若与计算机处理知识的方式吻合，则更加符合现代化教育的需求．在实现点几何解答系统的过程中发现，点几何体系的建立，符合知识工程的要求．而超过千例的计算机解题实践更是表明，点几何不仅符合数学直观，能更方便地表达基本几何事实，而且有助于几何推理的简捷化．下面仅举两例说明．

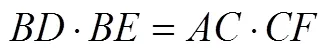
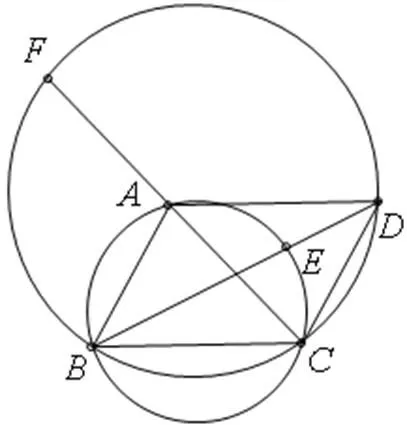
图3

证法1：

[0]：点、、、共圆

[1]：∠=∠(0)

[2]：是平行四边形

[3]：∥(2)

[4]：∠=∠(3)

[5]：∠=∠(1 4)

[6]：点、、、共圆

[7]：∠=∠(6)

[8]：△∽△(5 7)

[9]：/=/(8)

[10]：∠=∠(0)

[11]：∠=∠(3)

[12]：∠=∠(10 11)

[13]：∠=∠(0)

[14]：△∽△(12 13)

[15]：/=/(14)

[16]：/=/(9 15)

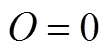
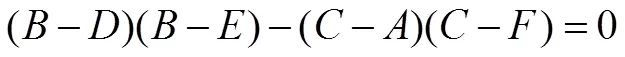
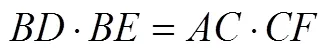
例2 如图4，△的边为定长，若边的中线为定长，试求顶点的轨迹．

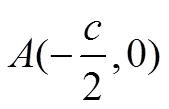
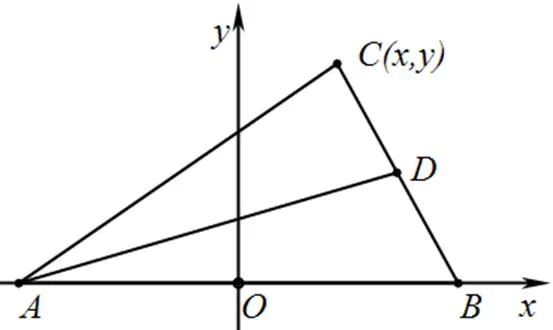
图4

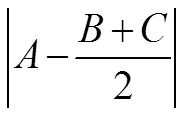
4 几何定理明证引发的思考

思考1：人类的证明是最好的么？

在AlphaGo的对战中，人类千百年来积累的千锤百炼的定式一次次被推翻．AlphaGo也走出了人类公认为坏棋的招法，但最终效果却很好．棋手们长期形成的围棋观被颠覆，需要重新思考：什么是好棋，什么是坏棋？

目前研究的机器解答，大多有一个定语，叫类人解答．也就是希望机器和人生成的解答尽可能类似，甚至是能混淆．这一方面是很早之前图灵测试的期待，另一方面也是教育应用的需要．问题是，人类解法也是多样的，有平凡无奇的俗解，也有构思奇特的巧解，甚至还有妙不可言的神仙手，如同天外飞仙，超出常人所想．

人类解法之中，有高有低，长期以来人工智能专家追求的是计算机模仿生成人类的一般解法，因为套路化，方便操作．智能解答领域，能否像AlphaGo那样，生成人类感到惊奇的解法呢．最新的研究表明，这是可能做到的．人给出的证明未必完美，机器证明可能超过人，给出更漂亮的解答．基于点几何恒等式算法完成的例题解答有着很好的可读性，因此具备出版并应用于中学教育的可能．目前已与两家出版社达成出版意向．华东师范大学出版社出版《点几何解题》，主要介绍点几何在解数学竞赛题方面的应用．科学出版社出版《点几何》，主要介绍点几何的教育价值和教育应用，以及自动推理算法介绍，并辅以翔实案例说明．这两本书里的题目，大部分来自人工收集，少部分由计算机自动生成，解答主要由机器完成，人只在其中增加少量连词和分析，使得读起来更加顺畅．计算机生成对联、诗歌早有先例，此次生成几何题集，在教育应用中效果如何，拭目以待．

思考2：解答能否比题干短？如何表示知识是最简短的？

已有数学家证明，有些定理即使最短的证明也会很长很长．那么对于一般的初等几何问题，证明最短能短到什么程度，能否短到与题干一样长，甚至更短？从“常识”来说，题干由若干条件和结论组成，条件看起来是零散的，条件之间存在隐藏的逻辑关系，而解答正是要把这些隐藏的逻辑关系找出来，隐藏关系显现化的过程常常需要引入其它定理来说明，这样才能将零散的条件（每个条件至少要用一次）串成一个完整的逻辑链，完成证明．这“必然”使得证明比题干要长，甚至有的要长几倍，甚至十几倍．一个两三行的几何题，证明花费一两页的，并不少见．这真的是必然的吗？

最近的研究表明，只要采取一种比较简洁而几何意义丰富的知识表示形式，以及找到一种简单的推理方式，是可以做到解答比题干还短的．推而广之，如何使得知识表示简单而意义丰富，推理简明容易实现，效率高且易于理解，这是一项很有研究意义又任重道远的工作．若能成功，即使是某一领域的部分成功，也能使得现有的推理体系大大简化，人们对事物之间关系看得更加清楚，大大减轻教与学的负担．

思考3：新的知识表示方式，可能造成原有的知识体系重新定位．

近几十年来，为了适应信息时代的需要，世界各国的中学数学教材都做了相应的改变，主要表现在对传统的初等数学进行了改造，渗透现代数学思想和方法．20世纪60年代，以新数学运动为代表的教育改革运动，喊出了“欧几里得滚蛋”“打倒欧家店”的口号．英国一位教授认为[20]：“这几十年来，学生没有学系统的平面几何，英国并没有出现科学人才危机，可见学不学欧氏几何无关紧要．”欧氏几何当然有其学习价值．只是信息时代需要学习的内容比以前大大增加了，而课时有限，如何进一步精简综合学习内容，值得研究．

欧氏几何自《几何原本》算起，已有两千多年．学习的难点，是构造千变万化的辅助线，使得图形中出现全等或相似图形．让学生掌握辅助线的添加，需要花费大量时间，但对进一步数学学习的用处却并不明显．而最新的点几何恒等式解题研究，其实质是将几何关系用向量形式表示，然后判断条件和结论之间是否“线性相关”．也就是表面研究的是初等几何，实际渗透的是高等代数的思想，为高等数学的学习打下基础．采用新的知识表示，会使得原来看似不相关的知识体系变得连通起来，对原来的知识体系的价值也要重新定位评估．在信息化高速发展的今天，知识体系的改造尽量符合知识工程的需求也是大势所趋．

[1] TURING A M. Computing machinery and intelligence [J]. Mind, 1950, 59 (236): 433-460.

[2] 吴砥，饶景阳，王美倩．智能教育：人工智能时代的教育变革[J]．人工智能，2019（3）：119-124．

[3] 马玉慧，柏茂林，周政．智慧教育时代我国人工智能教育应用的发展路径探究——美国《规划未来，迎接人工智能时代》报告解读及启示[J]．电化教育研究，2017，38（3）：125-130．

[4] 宋灵青，许林．人工智能教育应用的逻辑起点与边界——以知识学习为例[J]．中国电化教育，2019（6）：14-20．

[5] 张景中，李传中．自动推理与教育软件智能平台[J]．广州大学学报（综合版），2001，15（2）：1-6．

[6] 张景中．自动推理与教育技术的结合[J]．中国青年科技，2001（8）：26-28．

[7] BALACHEFF N. Processus de preuves et situations de validation [J]. Educational Studies, 1987, 18 (2): 147-176.

[8] TYMOCZKO T. The four-color problem and its philosophical significance [J]. The Journal of Philosophy, 1979, 76 (2): 57-83．

[9] 张晓贵．对数学证明的审查与数学可谬性[J]．科学技术哲学研究，2018（4）：58-62．

[10]  CHOU S C, GAO X S, ZHANG J Z. Machine proofs in geometry [M]. Singapore: World Scientific, 1994: 155.

[11]  YE Z, CHOU S C, GAO X S. Visually dynamic presentation of proofs in plane geometry [J]. Journal of Automated Reasoning, 2010, 45 (3): 213-241.

[12] 杨路，夏壁灿．不等式机器证明与自动发现[M]．北京：科学出版社，2008：152．

[13] 张景中．点几何纲要[J]．高等数学研究，2018（1）：1-8．

[14]  ZHANG J Z, PENG X C, CHEN M. Self-evident automated proving based on point geometry from the perspective of Wu’s method identity [J]. Journal of Systems Science & Complexity, 2019, 32 (1): 78-94.

[15] 张景中，彭翕成．点几何的教育价值[J]．数学通报，2019，58（2）：1-4，12．

[16] 张景中，彭翕成．点几何的解题应用：计算篇[J]．数学通报，2019，58（3）：1-5，58．

[17] 彭翕成，张景中．点几何的解题应用：恒等式篇[J]．数学通报，2019，58（4）：11-15．

[18] 彭翕成，张景中．点几何的解题应用：复数恒等式篇[J]．数学通报，2019，58（5）：1-4．

[19] 杨炳儒．基于内在认知机理的知识发现理论[M]．北京：国防工业出版社，2009：37．

[20] 张奠宙．数学教育改革的十个问题[J]．教育学报，1993（3）：12-15．

Thinking Inspired by Geometric Machine Certificate

ZHANG Jing-zhong1, 2, PENG Xi-cheng1, ZOU Yu2

(1. National Engineering Research Center for E-Learning, Central China Normal University, Hubei Wuhan 430079, China;2. Institute of Computing Science and Technology, Guangzhou University, Guangdong Guangzhou 510006, China)

The development of times requires intelligent education resources, rather than simple “electronic”. The basic requirement that intelligent solutions can be applied in the field of education is that they can be understood and accepted by people, that is, they have good readability. Our latest research suggests that human solutions are not necessarily the best, and that computers may offer surprising solutions. The fact that a computer gives a solution even shorter than the stem of the problem seems “contrary” to common sense, but it also leads to the question of how to represent knowledge in such a way as to be as concise and convenient as possible for reasoning. The innovation representation of knowledge should conform to the requirements of the information age as far as possible, and at the same time may cause the repositioning of the original knowledge system.

artificial intelligence; educational application; geometric theorems; machine certificate; knowledge representation and reasoning

2019-12-20

国家自然科学基金项目——点几何及其机器证明（11701118）

张景中（1936—），男，河南汝南人，中国科学院院士，研究员，博士生导师，主要从事机器证明、教育数学和教育技术研究．彭翕成为本文通讯作者．

G40-03

A

1004-9894（2020）01-0001-05

张景中，彭翕成，邹宇．几何机器明证引发的思考[J]．数学教育学报，2020，29（1）：1-5．

[责任编校：周学智、张楠]