高考数学命题质量评价的基础与方法
2020-02-28柯跃海陈清华
柯跃海,陈清华
高考数学命题质量评价的基础与方法
柯跃海,陈清华
(福建师范大学 数学与信息学院,福建 福州 350117)
高考数学命题的质量评价,对于高考数学命题质量的提高、高考数学核心功能的发挥,都有着显见的意义和价值.基于相关实践与研究提出:科学的高考数学命题质量评价,首先必须明辨评价的基础,包括准确解读评价的内涵、准确定位评价的视角和准确达成评价的共识;其次必须明确评价的方法,包括定性评价和定量评价的主要指标与实施流程.
高考数学;命题质量;命题评价
高考所承负的核心功能使其成为最受关注的考试,高考数学更是如此.每年高考结束后,关于高考数学试卷与试题的各种评价可谓“铺天盖地”:有以考生感受为角度做出的评价,有以教师认识为角度做出的评价,有以社会认同为角度做出的评价,还有以专家研究为角度做出的评价.
凡此种种,在让人目不暇接的同时,往往也因此不知所措:因为这些评价时常各执一词,甚至观点相背.其实,无论是从学术探讨的角度、还是从价值认同的角度,某些评价在观点上出现分歧都是可以理解的.问题在于,倘若未能及时弥合这些分歧,达成一致,高考数学在“导向教学”方面所发出的信息就可能被误读,更遑论以评价促进命题质量的提高.基于此,明辨高考数学命题质量评价的基础,明确高考数学命题质量评价的方法,其意义和价值都是显见的.
1 评价的基础
科学的高考数学命题质量评价,有赖于评价基础的明辨.这包括:评价内涵的准确解读,评价视角的准确定位,以及评价共识的准确达成.
1.1 评价内涵的准确解读
早在九百多年前中国北宋时期就已出现了“评价”一词,“市场不评价,市人知而不欺”(《北宋·戚同文传》).当然,这里的“评价”指的是“讨价还价、评论货物的价格”.上海辞书出版社出版的《辞海》(1999年版)对“评价”一词给出的解释是:评价,评论货物的价格……今亦泛指衡量人物或事物的价值.
据此可认为,高考数学命题质量评价指的是:根据命题依据(《普通高中数学课程标准(2017年版)》,以下简称为《课标》)和《××年普通高等学校招生全国统一考试大纲》(以下简称为《考纲》)所规定的内容与要求,运用可行的科学手段,对高考试卷与试题的命制质量进行价值判断,从而为提高高考数学命题质量、更加准确有效地体现高考数学的核心功能提供决策依据.
1.2 评价视角的准确定位
案例1 近年的高考数学几乎不考查“合情推理”,这是否意味着“合情推理”不适合作为高考的考查内容?
近年来,这类评价屡屡出现在高考数学试题分析中,反映的是对高考数学命题考查内容选取方式的理解问题,或者说是对高考数学命题质量评价视角定位的理解问题.
相关研究表明,以选拔为基本目标的高考数学命题,关注的是考生作为未来公民所必要的数学素养,关注的是考生进一步学习所必需的数学知识储备与数学能力储备.这种关注必然地决定了高考数学不是以知识的考查为唯一目标,知识的考查在相当大的程度上依赖于对能力或素养的考查.换言之,只要能够有效地考查考生的数学能力和数学素养,选择任何知识作为考查载体都是恰当的.
据此,在进行高考数学命题质量评价时,准确的视角应该是:试题是否遵从了《课标》和《考纲》所规定的内容与要求?是否突出了数学能力与数学素养的检测?而非纠缠于一些具体知识点的“考”或“不考”.
1.3 评价共识的准确达成
案例2 近年的高考数学在“应用意识”方面的考查方向与教材的关联度偏差太大——教材以较大比重介绍的求解实际应用问题的“函数模型”没有得到应有的体现.
这也是一类在近年来高考数学结束之后几乎都会出现的问题,所反映的是一种在“教考分离”趋势下必须修正但又普遍存在的认识——学生学了什么,高考就应该考什么.深究之下,这种认识产生的根源在于对《课标》《考纲》、学校所选用教材和高考数学命题之间关系把握的不准确.
相关研究表明,就科学的高考数学命题质量评价而言,《课标》《考纲》、学校所选用教材和高考数学命题之间的关系应该是:(1)《课标》是制定《考纲》的基本依据,也是高考数学命题的基本依据.(2)《考纲》是《课标》所规定培养目标的可测性细化,是高考数学命题的直接依据.(3)在课标课程教材“一标多本”的背景下,学校所选用的教材只是学生学习的载体,不能作为高考数学命题的依据.
当然,高考数学命题不会也不可能完全不顾及学校所选用的教材.一种认同度较高的做法是:适当关注教材在知识表述方面的特征,力求使高考数学试题的呈现方式与考生已有的学习经验没有明显的冲突.在这种认识下,案例2所涉及的问题也就不再是问题了:高考数学考查内容的选定,既不会完全受限于教材的内容安排(尤其是内容权重),更不会完全源之于命题人的“即兴生成”,而会是在严格遵循《考纲》相关规定的前提下,基于“合理抽样”而最终确定的.
2 评价的方法
高考数学命题质量评价的方法,包括定性评价和定量评价.两种方法相辅相成,不可偏废.
2.1 定性评价
所谓定性评价,是指评价者以《课标》和《考纲》为统领,在研读试卷的基础上,依据命题权重表和命题双向细目表,对试卷在《考纲》相关规定的遵循程度、考查目标的达成程度、表达呈现的规范程度等方面做出评价.定性评价的主要指标是5个命题原则(指导性原则、科学性原则、规范性原则、公平性原则和整体性原则)的遵循程度.
(1)指导性原则.指高考试题的命制必须在《课标》的统领之下,严格遵循《考纲》的相关规定与要求.
案例3 已知实数1,2,3和1,2,3满足:
①1+2+3=1+2+3;
②12+23+31=12+23+31;
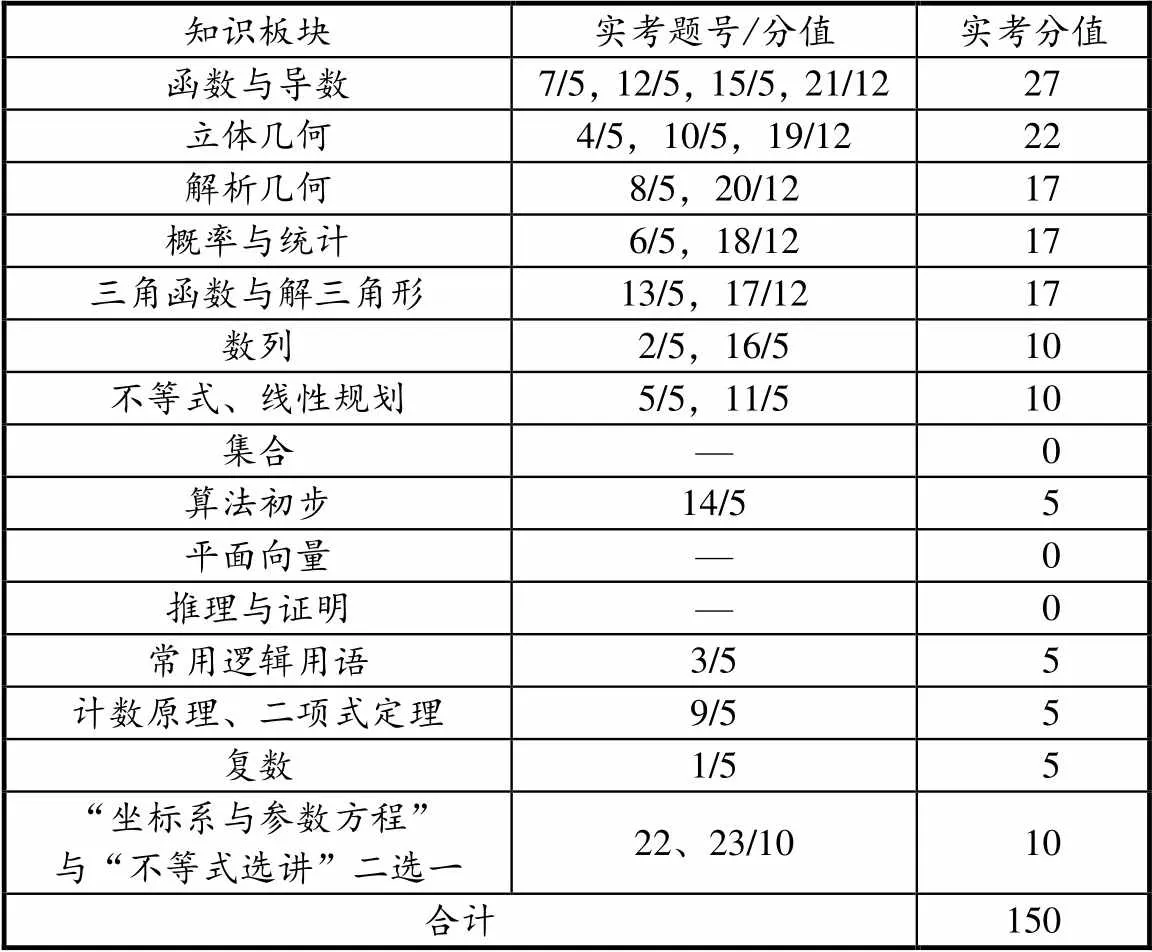
③ min{1,2,3} 试比较max{1,2,3}与max{1,2,3}的大小,并证明. 初中学段将“一元二次方程的根与系数关系”列为选学内容,高中学段也没有对其加以强调,因而求解本题所不可或缺的知识“一元三次方程的根与系数关系”也就不可能在《课标》和《考纲》中出现.换言之,倘若作为高考试题,则可以认为案例3的命制违背了指导性原则. (2)科学性原则.指高考试题的表述与解答都必须准确无误. 案例4 若函数()=e+2-e(R)的图象在点(1,())处的切线平行于轴,求函数()的单调区间. (3)规范性原则.指高考试题的表述必须符合数学表达的规范,确保试题的表述简洁、清晰、无歧义. (4)公平性原则.指高考试题对于所有考生而言必须是背景公平、解读与解答公平.换言之,试题的背景知识、解决试题所需的知识与方法应该为所有考生所熟悉、或为所有考生所不熟悉,在不影响知识与能力考查的前提下,必须规避与考试目的无关的背景材料. 应该认为,该题的预设考查意图在于解三角形和三角函数的相关知识与方法.但由于试题情境与“托勒密定理”完全一致,而运用“托勒密定理”求解本题远比运用解三角形和三角函数的相关知识与方法求解本题来得简单,这就使得本题的求解对不知道不属于《考纲》所规定的考试要求范围的“托勒密定理”的考生而言是不公平的,试题的公平性存在问题. (A)14 (B)13 (C)12 (D)10 命题者希望考生注意到方程2+2+=0未必是关于的一元二次方程,进而就是否等于零展开讨论,再整合讨论结果而得出答案.但问题在于,倘若考生直接将“方程2+2+=0”视为“关于的一元二次方程”,并借助根的判别式非负而得出≤1,则同样可以得出问题的正确答案.换言之,本题的解答对“优生”可能更为不利(耗费更多时间),试题的公平性存在问题. (5)整体性原则.指在试卷命制时,必须全面兼顾整个高中学段的学习内容,追求全面、合理的设置各种不同类型、不同难度要求的试题,以实现考试的目标. 案例8 高三毕业班质量检查试卷(理科数学)命题权重,如表1所示. 表1 高三质量检查试卷(理科数学)命题权重 基于整体性原则,案例8所呈现的数据表明:(1)相应试卷的考查内容抽样没有较为全面地兼顾整个高中学段的学习内容,如缺失“集合”“推理与证明”“平面向量”等内容.(2)相应试卷中部分知识板块的考查难度设置不甚合理,如:旨在考查“函数与导数”的试题在同类题型的试题中题序相对靠后,表明预设难度整体偏难;旨在考查“三角函数与解三角形”的试题在同类题型的试题中题序相对靠前,表明预设难度整体偏易. 所谓定量评价,是指评价者以高考数学核心功能的体现为统领,以考查目标为指导,借助阅卷所得出的数据,对考试结果的真实性和有效性、试卷与试题的难易程度和区分程度等方面做出评价. 定量评价的主要指标为信度、效度、难度和区分度. (1)信度.信度是指考试结果的稳定性或可靠程度,亦即考试结果是否真实、客观地反映了考生的实际水平. 信度指标多以相关系数表示.相关系数大致分为稳定系数(跨时间的一致性)、等值系数(跨形式的一致性)和内在系数(跨项目的一致性).就高考命题质量评价而言,等值系数是较为适宜的信度指标表现形式. 水平. (2)效度.效度是指考试结果的准确性和有效性的程度,亦即考试达到预期目的的程度.程度越高,效度越高.1974年美国心理学会颁发的《教育和心理测验的标准》将效度分为3大类:内容效度、效标关联效度和结构效度. 高考数学命题质量评价通常以内容效度作为效度的表现形式,并综合借鉴内容效度的3种评估方法(专家判断法、统计分析法和经验推测法),借助考试结果的分布散点图(所有被试的分数由低到高排序后,以序号和分数分别作为点的横坐标和纵坐标)来估计效度. 一般地,若散点图可近似看作椭圆的左上侧1/4部分,且该椭圆的离心率与0.5的误差足够小,则可认为考试结果的准确性和有效性的程度较高,亦即考试基本达到了预期的目的.就高考数学命题而言,|-0.5|<0.01是应达到的效度要求. (3)难度.难度是指考试试题的难易程度.计算方式为: 试题的难度,表示正确应答试题的考生人数,表示考生的总人数[1]. (4)区分度.区分度指考试对考生实际水平的区分程度. 具有良好区分度的考试,实际水平高的考生应该得高分,实际水平低的考生应该得低分.因而,区分度又称鉴别力,是评价试卷和试题质量的主要依据.区分度通常采用极端分组法计算,即首先对所有考生的考试得分由高到低进行排序,取前25%作为高分组,后25%作为低分组,而后依照下列公式进行计算. ③试卷的区分度计算公式为:=11+22.其中,表示试卷的区分度,1、2分别表示客观题、主观题的区分度,1、2分别表示客观题、主观题的分值权重.就高考数学命题而言,区分度必须不小于0.5. 高考数学命题质量的定性评价以“指导性、科学性、规范性、公平性和整体性”的遵循程度为主要评价指标,一般流程为:评价准备→试卷研读→定性分析→形成报告. (1)评价准备.这是定性评价的基础.包括:①研读命题依据,即研读《课标》和《考纲》;②研读命题要求,即研读命题规范要求、命题原则和命题技术;③研读题型考查功能,即研读选择题、填空题、解答题等题型考查功能. (2)试卷研读.这是定性评价的基础保障,是定性分析的前提.包括:①研读试卷的总体结构;②研读试卷的考查目标;③研读试题与试卷的指导性、科学性、规范性、公平性和整体性;④研读试题答案的科学性、普适性和规范性. (3)定性分析.这是定性评价的主要环节.包括:①试卷的总体结构分析,即分析试卷在题量、题型设置以及相应的分值配置等方面与《考纲》的相关规定之间的契合程度;②试卷的考查目标分析,即分析试卷在内容、思想方法以及能力等方面的考查与《考纲》的相关规定之间的契合程度;③试卷的整体效应分析,即分析试卷所设置的各种题型的考查功能的发挥情况,分析所有试题考查功能合力的形成情况;④试题与试卷的“五性”分析,即分析试题与试卷在指导性、科学性、规范性、公平性和整体性等方面是否存在问题;⑤试题答案的“三性”分析,即分析试题答案在科学性、普适性以及规范性等方面是否存在问题. (4)形成报告.在定性分析的基础上,将分析所得的结论以报告的形式呈现.必须注意,呈现的报告虽为定性评价的结论,但相关分析仍应尽量以图表的形式呈现. 高考数学命题质量以“信度、效度、难度和区分度”作为定量评价的主要指标.基本流程为:评价准备→数据处理→定量分析→形成报告. (1)评价准备.这是定量评价的基础.包括:①研读定性评价报告;②研读评价的基本维度、掌握计算方法;③收集相关数据. (2)数据处理.这是定量评价的基础保障,是定量分析的前提.包括:①主观题与客观题得分统计;②信度、效度、难度以及区分度的计算. (3)定量分析.这是定量评价的主要环节,包括:①信度分析;②效度分析;③难度分析;④区分度分析;⑤考生答卷情况分析. (4)形成报告.在定量分析的基础上,将分析所得的结论以报告的形式呈现. 需要指出的是,高考数学命题质量评价必须在关注定性评价与定量评价的同时,追求二者的有机融合.换言之,在定性评价和定量评价的基础上,评价者还必须全面考虑考试的总体情况,并以综合评价报告的形式予以体现. 依托相关研究的理论与实践,从评价的内涵、视角和共识等3个方面厘清了高考数学命题质量评价的基础,从定性与定量两个层面阐释了高考数学命题质量评价的方法,为高考数学命题质量评价提供了理论依据和实操办法. 由于高考数学命题的核心功能是立德树人、服务选拔、导向教学.因而,就全面性而言,高考数学命题的质量评价应该涵盖上述3个方面,限于篇幅,这里略去了高考数学命题在“立德树人”“导向教学”两方面的质量评价.这样的做法虽有失全面,但仍可“管窥知全豹”:无论是基于“立德树人”“导向教学”,还是基于“服务选拔”而审视高考数学的命题质量,其根本目的都在于,以科学的评价助推命题质量的不断提升、促进命题功能的有效发挥.这就意味着,评价基础的明辨和评价方法的明确始终是不可偏废的两个方面.相关实践证明,唯有如此,高考数学命题质量评价所言及的“前事之鉴”,方可成为“后事之师”! [1] 胡中锋,李方.教育测量与评价[M].广州:广东高等教育出版社,1999:36,51,56. [2] 雷新勇.大规模教育考试:命题与评价[M].上海:华东师范大学出版社,2006:1-5,8,13-18. [3] 马忠林.数学教育评价[M].南宁:广西教育出版社,1996:391-394. [4] 任子朝,王蕾,朱乙艺,等.标准参照考试理论在高考中的应用——以H省2010—2012年高考理科数学为例[J].数学教育学报,2013,22(3):1-4. [5] 任子朝,周远方,陈昂,等.高考数学科考核目标研究[J].数学通报,2013,52(7):1-8. [6] 任子朝.高考数学试卷结构效度分析[J].数学教育学报,1995,4(3):40-43. [7] 任子朝.能力立意命题的理论与实践[J].数学通报,2008,47(1):24-28,32. [8] 陈昂,任子朝.数学高考中实践应用能力考查研究[J].数学教育学报,2017,26(3):15-18. [9] 杜文久.数学测验中主观题的评分问题[J].数学教育学报,2006,15(3):87-88. [10] 张瑞炳,倪明.中国和俄罗斯高考数学考查内容比较研究[J].数学教育学报,2016,25(2):32-35. [11] 刘耀斌.谈对学生数学测验的评价[J].数学教育学报,2008,17(6):63-65. [12] 柯跃海,陈清华.高考数学:命题目标的确立与实现[J].数学通报,2013,52(1):56-58,60. The Foundation and Method of the Quality Evaluation of Mathematical Propositions in College Entrance Examination KE Yue-hai, CHEN Qing-hua (School of Mathematics and Informatics, Fujian Normal University, Fujian Fuzhou 350117, China) The quality evaluation of mathematical propositions in college entrance examination has obvious significance and value for improving the quality of mathematical propositions in college entrance examination, and accurately plays core functions of mathematics in college entrance examination. Based on relevant practice and research, we propose that the scientificity of quality evaluation of mathematical propositions in college entrance examination, firstly is essential to clearly distinguish the basis of evaluation, including accurately interpreting the connotation of evaluation, accurately positioning the perspective of evaluation and accurately reaching the common view of evaluation, secondly, to define the methods of evaluation, including the main indicators and implementation process of qualitative and quantitative evaluation. mathematics in college entrance examination; propositional quality; propositional evaluation 2019–09–08 全国教育科学“十三五”规划2016年度教育部重点课题——高中生数学核心素养培养的策略及评价研究(DHA160364);福建省教育科学“十三五”规划2018年度课题——学科核心素养导向的中学数学教学设计(FJJKCG18-044) 柯跃海(1963—),男,福建泉州人,副教授,硕士生导师,主要从事数学考试的命题与评价研究. G40–058.1 A 1004–9894(2020)01–0048–04 柯跃海,陈清华.高考数学命题质量评价的基础与方法[J].数学教育学报,2020,29(1):48-51. [责任编校:陈隽、张楠]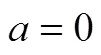
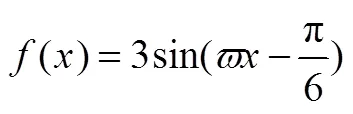
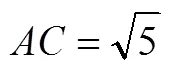
2.2 定量评价
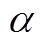
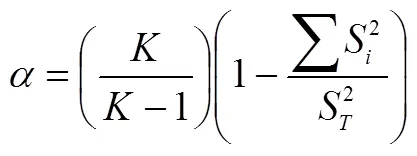
3 评价的实施
3.1 定性评价的实施
3.2 定量评价的实施
4 结论与展望
