基于Fuzzy-AHP质疑式数学核心素养评价指标体系的研究

傅海伦张 丽王彩芬

基于Fuzzy-AHP质疑式数学核心素养评价指标体系的研究

傅海伦1，张 丽1，王彩芬1，2

（1．山东师范大学 数学与统计学院，山东 济南 250358；2．青岛大学 数学与统计学院，山东 青岛 266071）

数学核心素养培养是当下基础教育数学课程与教学改革的热点．培养学生的质疑能力和创新精神，建立科学合理的数学核心素养评价指标体系是当下迫切需要解决的问题．质疑式学习包括认知性质疑、迁移性质疑、创造性质疑．质疑式3维空间学习模式搭建了数学核心素养框架与课堂衔接的“立交桥”；“634”质疑式学习发展空间模式，实现了数学学习过程的“提档增速”．利用AHP软件及模糊综合评价法构建的质疑式数学核心素养评价指标体系，有助于促进学生数学学科的高效学习及核心素养水平的提高．

质疑式；634学习发展空间模式；数学核心素养；评价指标体系

1 研究缘起与基础

数学核心素养是当下基础教育数学课程与教学改革的热点．充分“问诊”学生数学核心素养培养“现状”，“把脉”学生数学核心素养问题“痛点”，探寻学生数学核心素养培养精准“处方良药”，是助力搭建核心素养与人才培养的“立交桥”，也是制定契合教学新策略的前提．2017年张建桥提出基于核心素养的教学策略在从教学方法上应讲授主导型走向发展主导型，在教学评价上应从单一的标准走向综合的评价系统进行转型．所以适切的教学模式及可行的评价体系是研究的着力点[1]．

学生核心素养是指学生成功应对实际生活中进行学习所需要的“胜任力或竞争力”[2]．学科核心素养既能体现学生发展核心素养的通适基础[3]，也能体现学科自身的专业特点．基础数学学科中凸显核心素养的重要内容之一就是培养学生的质疑能力和创新精神．质疑式学习方式致力于真实情境和问题驱动下的数学课堂教学观、学习观的转变，注重在教师的引导下，学生主体性的充分发挥，启迪学生主动发现问题、思考问题、分析问题，探寻问题的策略和方法，并鼓励质疑问难，提出独到见解，在培养学生有理由、有根据地学会数学学习、思考和表达的基础上，提升学生批判性的思维品质，进而充分培养学生的质疑能力和创新精神．在质疑式背景下，应当建立何种数学核心素养评价指标体系，科学合理地评价数学核心素养培养质量，进而助力学生质疑、发散和创新能力的提升是当下迫切需要解决的问题．

2012年在傅海伦教授指导下的山东大学附属中学正式提出“以问题为导向、以学生为中心，以质疑为特征”的质疑式学习模式[4]．质疑式教学是建立在教育学和教育心理学的基础之上的教学方法和认识方法[5]．质疑即提出疑问，质疑能力在数学学习过程中起着至关重要的作用．质疑式学习正是以问题为导向，以启发为手段，以知识为载体，以思维为灵魂，以质疑为特征，以培养学生学会学习、解决疑惑、体会成功喜悦为目的开展课堂教学．依据学习心理学和认识发展的原理，质疑式学习包括：认知性质疑——针对课程、教材、教法的质疑；迁移性质疑——针对权威、推理、应用的质疑；创造性质疑——针对方法、推广、创新的质疑的三维立体空间学习模式．

质疑式三维立体空间学习模式能够搭建“数学核心素养”框架与课堂衔接的“立交桥”．“问题是数学的心脏”，质疑式三维立体空间学习模式倡导让学生提出问题，学生的这种“知其然不知其所以然”的困惑就成为推动数学课堂教学的内驱力．在此基础上，通过观察、探究、实践等教学活动，启发学生进行自主探究、情境合作等质疑式学习，培养学生的探究意识、质疑精神和理性思维，提高学生适应未来社会生活和解决问题的能力．因此，这种模式能够在课堂上全面深入地体现数学核心素养思想的教学要求，提升学生数学核心素养水平，实现数学学习过程的“提档增速”，从而打造能让数学核心素养落地的求真、求实课堂．

首先，在质疑式三维立体空间学习模式中，可以进行深层次心灵沟通与精神交融的动态交流过程．通过精准定位学生思维的“最近发展区”，形成真正的“师生学习共同体”，开阔师生合作交流新视角，从而融入“核心素养”．同时，通过质疑式学习的过程与方法的展示与指导，可以充分挖掘和发展学生各方面的潜能，在思考中获取知识，体验数学学科发展历程，让学生会质疑、探究、分析、反思和总结，提升问题解决能力，促进全面发展．

其次，质疑式教学方式使数学学习过程更加生动活泼、积极主动，富有趣味性和挑战性，在重视了知识教学结果的同时又兼备了教学过程．通过开展质疑式提问，点拨发散学生的思维，可以帮助学生选择恰当的质疑方法和技巧，找准问题，对症下药．学生依靠已有的认知、经验和思维水平，经过教师的引导和启发，进一步促进学生数学思维能力和数学素质的培养．

再次，质疑式3维立体空间学习模式以问题为导向，问题质疑是培养学生“数学核心素养”的关键因素．精心设计不同层次的探索问题，可以建立问答性、愤悱性、探究性、批判性的质疑问题链条，以挖掘学生对知识认知、情感态度的不平衡状态，启发和引导学生强烈的求知欲，从而启迪学生积极主动地对数学知识进行从感悟认知到概括迁移，再到创新创造的质疑过程，最终提升学生对知识的发散和创新能力，逐步攀登“学会”—“会学”—“乐学”的学习阶梯．

2 “634”质疑式学习发展空间模式的提出

通过实践研究发现，质疑式数学核心素养体系学习过程是一个动态发展的系统性过程．

“6”是“六核心”，在最新版的课程标准进一步完善了中学生需要具备的数学素养的要求，明确指出中学生的数学素养由6个部分的素养组成，即“六大核心要素”——数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析．它强调知识、能力、态度的统整，凸显了情感、态度、价值观的重要性，是人们选择问题策略时所体现的数学思想和数学品质[6]．

“3”即“三维”，中国学生发展核心素养总体框架涉及文化基础、自主发展及社会参与3个方向,包含人文底蕴、科学精神、学会学习、健康生活、责任担当、实践创新6个方面[7-8],将学生发展核心素养总体与学科进行有机结合．研究者建立了“三维”质疑式数学核心素养培养新模式：即“智慧—认知性质疑”“融合—迁移性质疑”“和谐—创造性质疑”3维学习发展空间模式（如图1）．

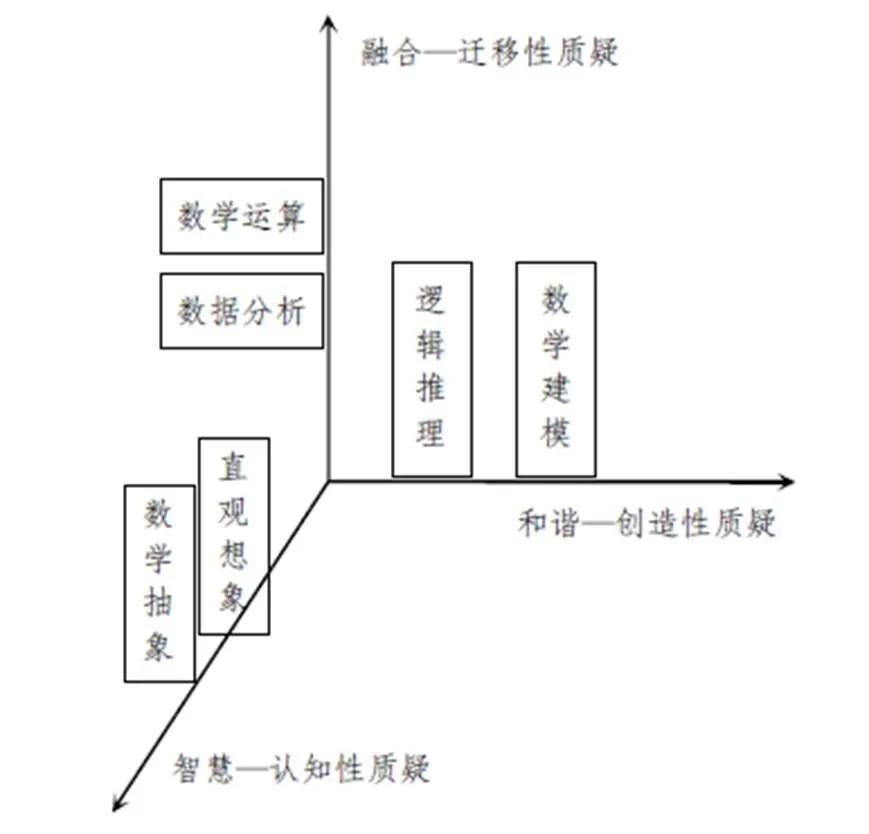
图1 质疑式数学核心素养三维模型

“智慧—认知性质疑”即在抽象的数学知识海洋中充分挖掘学生的智慧因素，包括对数学知识的认同感、信任感和审美能力；让学生探索奇妙的数学世界，享受迷人的数学旋律，反思领悟数学知识，掌握数学基本技能，从而欣赏并热爱数学学科．这与数学核心素养中的数学抽象、逻辑推理相对应．“融合—迁移性质疑”即通过问题质疑、自主探索、合作交流，充分挖掘学生强烈的求知欲．培养学生思维缜密性，严谨的数学品质，善于运用已认知的规律和方法，进行知识的拓展迁移，在探寻简单纯朴的数学规律旅程中，体验柳暗花明又一村之感．这与数学核心素养中的数学运算、数据分析相对应．“和谐—创造性质疑”即在数学学科培养过程中注重体现精神、文化、情感态度和价值观．能够让学生更加从容、积极、乐观地迎接数学问题与挑战，体验数学的美妙和谐，创新发散数学思维．执着专注于严肃缜密的数学精神，有助于学生对数学学科充满强烈的好奇心、求知欲、喜悦感和成就感的积极向上的内心体验．文以载道、文以化人，逐步形成顽强、坚韧、严谨、灵活和包容的人格品质，培养会表达、懂思想、有责任、善创新的“和谐”的人．这与数学核心素养中的直观想象、数学建模相对应[9-12]．

“4”是“四层次”，即在对学生质疑式数学核心素养指标体系评价结果的4个层次的划分．对数学核心素养的测量要以知识为基础,以数学思想方法为引领,以情境为载体,注重综合性和层次性[13]．2018年喻平提出对数学核心素养,宜采用知识理解、知识迁移、知识创新来刻画．质疑式学习强调学生质疑反思领悟能力的培养[14]，结合布鲁纳发现主义学习理论，学习者主动构建知识体系的学习过程．通过专家调研及教学实践，研究者增加了一个评价维度即知识的反思领悟、技能掌握、拓展迁移及发散创新．反思领悟指学生主动思考、质疑探究和发现问题的能力；技能掌握指学生掌握基础知识、形成基本技能；拓展迁移指学生将知识应用到新的情境中去解决问题的能力；发散创新指学生提出问题、推广问题的能力．这样划分数学核心素养水平，能反映数学课程目标的内核，具备学业质量测评的操作性特征，递进式地提高学生在质疑式学习过程中的数学核心素养水平，有效掌握学生智慧潜力挖掘程度、充分了解学生学习水平，激发学生学习的内生动力．

每个核心素养即相对独立又互相渗透，是有机联系的整体．在“634”质疑式数学核心素养指标体系中（如图2），强调数学核心素养的两两相对独立性，有助于清晰地反映各个数学核心素养的重要程度，以适时、适度、适当地对数学核心素养指标体系进行积极、动态、全方位的调整和完善[15-26]．

图2 “634”质疑式数学核心素养框架结构

3 基于APH的质疑式数学核心素养评价指标体系构建

基于导向性、科学性、可行性、发展性、动态性、整体性等原则，通过线上选取经验丰富的教学一线和管理教师、专家发放调查问卷200份，回收137份，利用软件yaahp进行一致性检验，最后确定120份有效问卷．利用SPSS软件对选取的指标进行重要性和变异系数分析和选取，最终确定质疑式数学核心素养评价基本指标体系（如图3）．由于受篇幅限制，各个专家单独数据分析结果未给出．

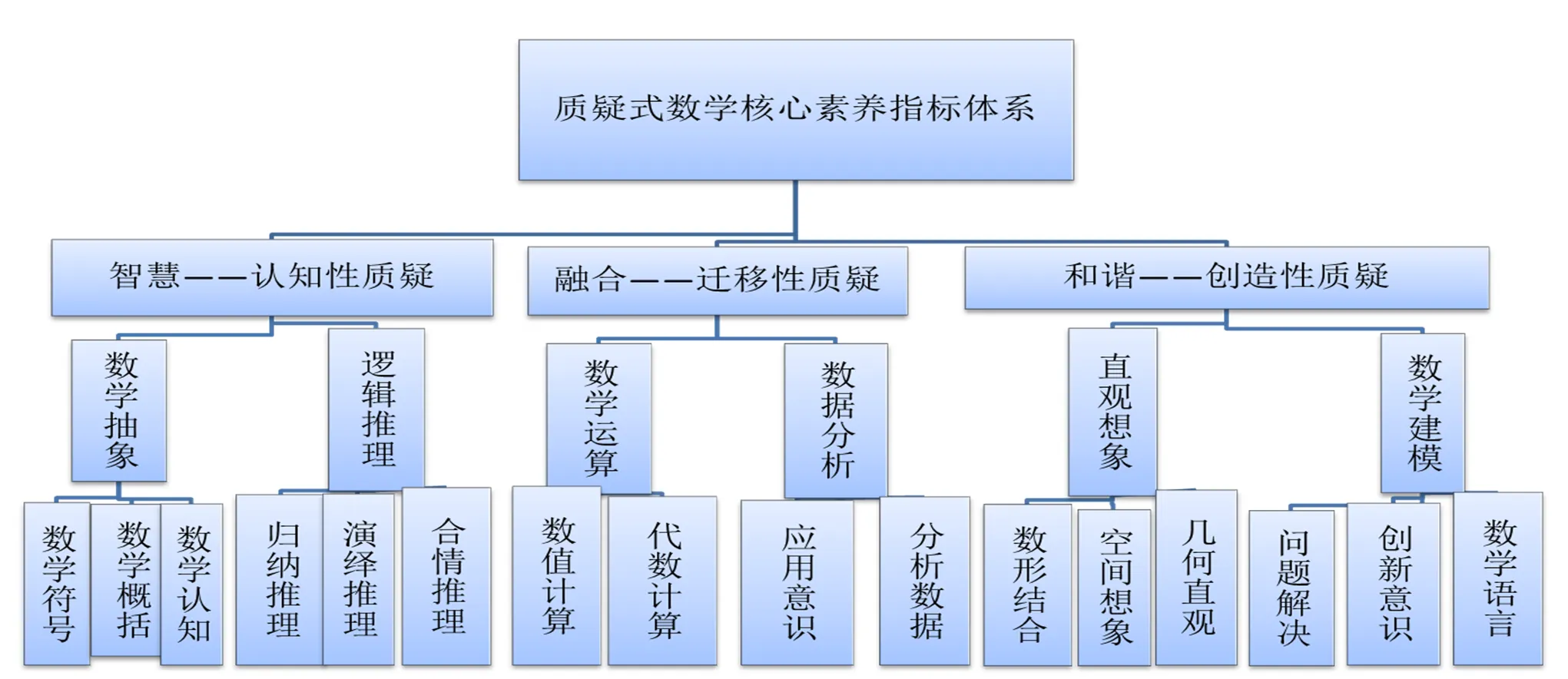
图3 质疑式数学核心素养指标体系层次模型

由于质疑式数学核心素养评价因素大部分具有模糊性，较难给出精确划分，为使指标体系更科学、更准确，研究者采用AHP法确定指标体系的权重．AHP是由美国运筹学家Saaty提出，是将决策总是有关的元素分解成目标、准则、方案等层次[27]，是一种定性和定量相结合的、系统化、层次化的多准则决策分析方法，正好为此类问题提供新路径和新方法．具体步骤如下．

3.1 建立各层次之间的递阶结构模型[27]

层次分析递阶结构模型由目标层、准则层、指标层构成．目标层包含一个因素；准则层为中间环节，涵盖数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析6大要素；指标层也叫评估层，共包含16个指标．

3.2 两两构造比较判断矩阵[27]

利用Saaty提出1~9的比例标度法两两比较，评价等级按表1中的重要等级及其赋值进行．

表1 元素两两对比时的重要等级及其赋值

3.3 单层次及总排序

计算每个矩阵的最大特征根max和特征向量，做一致性检验．特征向量的每个指标对应每层元素相应于上层某一个准则的权重．使用相对权重加权平均的方法可以得出组合权重系数，并检验组合的一致性[27]．

（1）将判断矩阵中的元素按行相乘，即

（2）计算

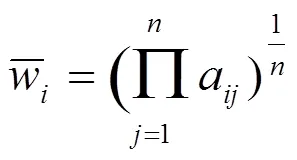
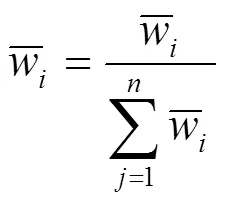
=[1,2, …, w]即为所求特征向量．

（4）计算最大特征根

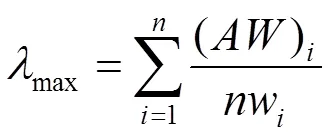
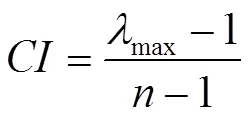
其中表示判断矩阵的阶数．

（6）根据表2选取对应的．

表2 一致性指标

（7）计算一致性比例，

当<0.1时，认为一致性可接受[27]．

3.4 一级指标和二级指标权重系数的计算[27]

利用yaahp软件，构建“634”质疑式数学核心素养指标体系层次模型，建立一级、二级指标权重矩阵，并分别计算各指标权重．具体结果如图4~7．

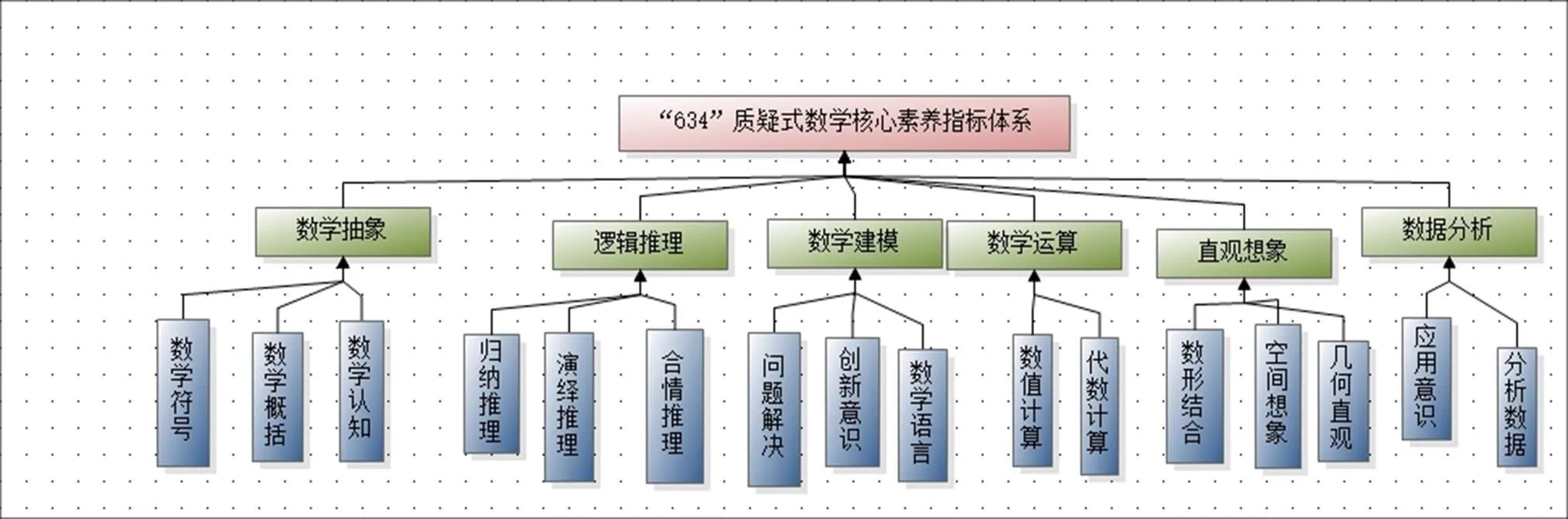
图4 yaahp软件层次结构模型构造界面

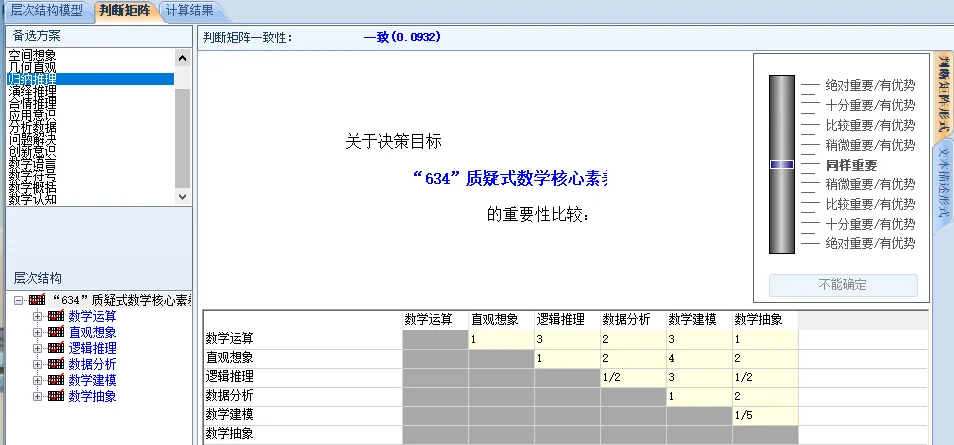
图5 yaahp软件判断矩阵计算界面

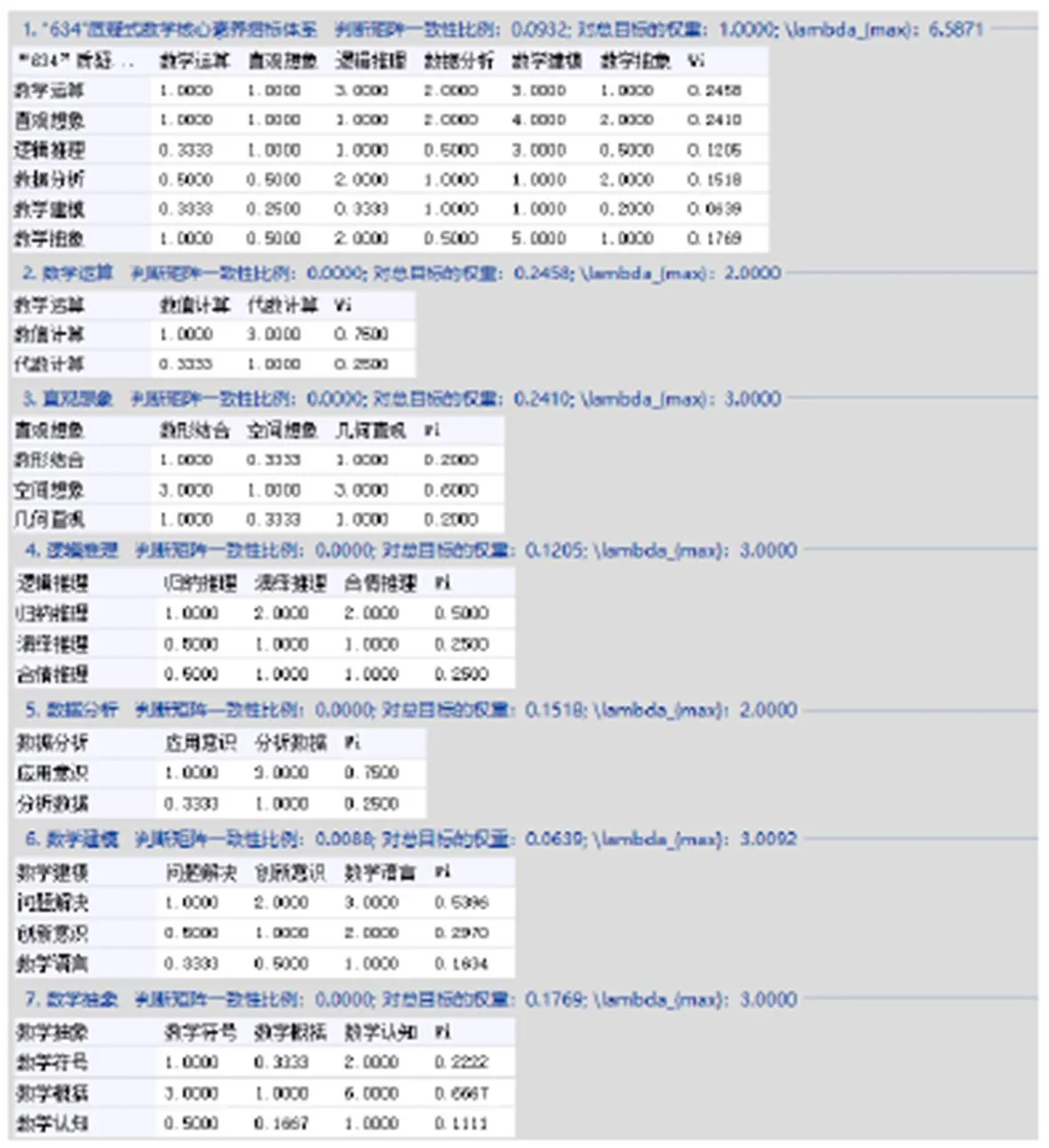
图6 yaahp软件计算详细数据界面

图7 yaahp软件计算结果输出界面

由一级指标权重可看出，占较大比重的为数据运算、直观想象和数学抽象这3个素养指标，非常契合当下基础教育数学课改、教改及高考改革倡导的理念，充分强调并重点培养学生的应用实践、融合迁移及创新发展能力．

4 基于Fuzzy-APH的质疑式数学核心素养评价指标体系的实践研究

由此确立“634”质疑式数学核心素养指标体系权重数据库，并利用Fuzzy综合评价法对评价指标体系进行实践．在线上发100份调查问卷（回收100份），对指标体系进行评价，评语集分为4个评价等级[28]（反思领悟、技能掌握、拓展迁移、发散创新），例如有25人对某指标评定为“发散创新”层，则统计结果为0.25，以此来确定每个指标隶属中评价等级的隶属度．最终“634”质疑式数学核心素养评价指标体系权重数据库如表3．

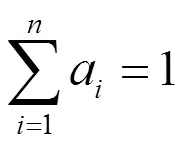
按照每个U分别进行模糊综合评价，得到一级综合评价的模糊向量[28]为：

1=(0.16 0.21 0.49 0.21)

2=(0.17 0.32 0.34 0.21)

3=(0.15 0.29 0.38 0.21)

4=(0.19 0.27 0.38 0.16)

5=(0.20 0.28 0.37 0.22)

6=(0.21 0.32 0.34 0.17)

B=(b1,b2,…,b)=AºR，

b=max{min(a1,r), min(a,r)} (=1, 2, …,；=1, 2, …,；=1, 2, …,)．

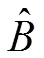
表3 “634”质疑式数学核心素养评价指标体系权重数据库权重集合

5 基于“634”质疑式数学核心素养评价指标体系的启示

5.1 探索发现质疑式数学核心素养培养的关键因素

通过测评了解学生质疑式数学核心素养的层次水平，分析研究数据结果，探索发现了质疑式数学核心素养培养的关键因素，在质疑式学习过程中，数学核心素养按其重要性排序依次为：数据运算、直观想象、数学抽象、数据分析、逻辑推理和数学建模．其中数据运算、直观想象和数学抽象是重要成分；问题解决、应用意识和创新意识是当下需要重点培养的数学关键能力；数学建模素养与解决问题能力密切相关，也是数学能力培养的重点．

5.2 有助于教师常态化了解学生学习水平信息

研究者以如何评价数学核心素养这一实际问题为导向，提出“六核心四层次三维度空间理论”，并尝试构建“634”质疑式数学核心素养评价指标体系，其中包含6个一级指标和16个二级指标．在方法上，综合利用Fuzzy-AHP科学评价法，分析得出各个指标的权重，将指标体系进行评价实践，实现数学高效学习的精准定位，教师可以根据评的结果对学习中的问题进行有针对性地诊断，学生可以依据评价的内容对自身的学习重点、方法进行有目的地侧重和改进，从而提升学生的数学核心素养水平[28]．

5.3 促进学生的全面发展

“634”质疑式数学核心素养体系不仅充实了学生数学核心素养评价的理论体系，而且丰富了教育评价的手段，为数学核心素养的评价提供了实用的方法．质疑式数学核心素养培养体系的学习过程是动态发展的、系统性的．就学校而言，其它学科的教师也可通过数据更好地了解班上学生的学习特点，因为学科之间存在共性．比如数学抽象和数学语言层次较高的学生往往在英语和语文的学习上有一定优势，那么相关教师就应找准这一特征因材施教．

如何在学校教育中发展核心素养，如何让“634”质疑式数学核心素养指标体系在基础教育阶段数学人才培养目标达成过程中发挥更加积极的作用，如何常态化地动态调整、完善指标体系框架，探寻更加适合的评价方法，从而增进基础教育阶段数学的育人功能，将成为今后持续研究的方向．

[1] 张建桥．培养学生核心素养亟待教学转型[J]．中国教育学刊，2017（2）：6-12．

[2] 王卫华．普通高中学科核心素养与学生发展核心素养的对接探析[J]．课程·教材·教法，2018，38（6）：84-90．

[3] 陈佑清．“核心素养”研究：新意及意义何在？——基于与“素质教育”比较的分析[J]．课程·教材·教法，2016，36（12）：3-8．

[4] 王道远，傅海伦．质疑式数学课堂教学研究案例试析[J]．中学数学杂志，2013（8）：10-13．

[5] 傅海伦，薛海东，韩颖．论数学课堂质疑式教学及其心理学意义[J]．数学教育研究，2014（2）：1-4．

[6] 傅海伦，于复海，薛海东，等．数学质疑式预习导案与课堂问案设计与分析[J]．中国数学教育，2014（3）：26-31．

[7] 任艳华．核心素养与学科核心素养的有机对接[J]．中国教育学刊，2016（S2）：74．

[8] 刘霞，胡清芬，刘艳，等．我国学生发展核心素养的实证调查[J]．中国教育学刊，2016（6）：15-22．

[9] 王光明，卫倩平，赵成志．核心素养视角下的跨学科能力测评研究[J]．中国教育学刊，2017（7）：24-29．

[10] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23．

[11] 洪亮．学生发展核心素养在小学数学中的渗透路径探析[J]．中国教育学刊，2017（6）：72-74．

[12] 朱立明．基于深化课程改革的数学核心素养体系构建[J]．中国教育学刊，2016（5）：76-80．

[13] 任子朝，陈昂，赵轩．数学核心素养评价研究[J]．课程·教材·教法，2018，38（5）：116-121．

[14] 喻平．基于核心素养的高中数学课程目标与学业评价[J]．课程·教材·教法，2018，38（1）：80-85．

[15] 于川，朱小岩，邬楠，等．高中生数学学科核心素养水平调查及分析[J]．数学教育学报，2018，27（2）：59-64．

[16] 裴昌根，宋乃庆，乔卉，等．数学学习兴趣测评指标体系的构建与验证[J]．教育教育学报，2018，27（2）：70-73．

[17] 董林伟，喻平．基于学业水平质量监测的初中生数学核心素养发展状况调查及分析[J]．数学教育学报，2017，26（1）：7-13．

[18] 王光明，刘丹．初中生数学学习策略调查问卷的设计与编制[J]．数学教育学报，2017，26（3）：19-24．

[19] 王娅婷，毛秀珍．数学素养的测量及评价[J]．数学教育学报，2017，26（3）：73-77．

[20] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-6．

[21] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1．

[22] 桂德怀，徐斌艳．数学素养内涵之探析[J]．数学教育学报，2008，17（5）：22．

[23] 潘小明．关于数学素养及其培养的若干认识[J]．数学教育学报，2009，18（5）：23．

[24] 孙成成，胡典顺．数学核心素养：历程、模型及发展路径[J]．教育探索，2016（12）：27-30．

[26] 蔡金法，徐斌艳．也论数学核心素养及其构建[J]．全球教育展望，2016，45（11）：3-12．

[27] 王晓华．基于AHP的数学试题难度模糊综合评判[J]．教育科学，2013，29（5）：38-43．

[28] 杨林，余半坡．基于Fuzzy和AHP的高校教育教学质量评价方法研究[J]．中国校外教育，2014（27）：61-62．

Research of Evaluation Index System about the Skeptical-Mathematics Key Competencies Based on the Fuzzy-Analytic Hierarchy Process

FU Hai-lun1, ZHANG Li1, WANG Cai-fen1, 2

(1. School of Mathematics and Statistics, Shandong Normal University, Shandong Jinan 250358, China;2.School of Mathematics and Statistics, Qingdao University, Shandong Qingdao 266071, China)

The cultivation of students’ mathematical core literacy was the hot spot in the current mathematics curriculum and teaching reform. Cultivating students’ skeptical learning ability and innovation spirit and establishing scientific and reasonable evaluation index system of mathematics core literacy were urgent problems to be solved. By constructing a skeptical three-dimensional spatial learning model, a bridge between core literacy framework of mathematics and classroom was built. The “634” skeptical learning development space model was proposed to achieve the “growth rate” of mathematics learning process; On this basis, using AHP software and fuzzy comprehensive evaluation method, a system of evaluation index for the core literacy of skeptical mathematics was tried to be built, and was applied in the field of mathematics education and teaching. It could explore the key factors for the cultivation of the core literacy of skeptical mathematics. In this way, the efficient learning of students’ mathematics subjects was promoted and the core literacy levels could be much improved.

skeptical learning; “634” learning development spatial model; mathematics key competencies; evaluation index system

2019-09-27

教育部人文社会科学研究项目——数学质疑式教学模式创新与实效研究（17YJA880020）

傅海伦（1970—），男，山东曹县人，教授，博士生导师，主要从事课程与教学论（数学）与数学文化研究．

G421

A

1004-9894（2020）01-0052-06

傅海伦，张丽，王彩芬．基于Fuzzy-AHP质疑式数学核心素养评价指标体系的研究[J]．数学教育学报，2020，29（1）：52-57．

[责任编校：陈汉君、陈隽]