考虑不对称性的地铁旅客支付及受偿意愿研究

陈 欣，罗 霞*，刘春禹，刘永红

(西南交通大学a.交通运输与物流学院;b.综合交通运输智能化国家地方联合工程实验室,成都611756)

0 引 言

支付意愿(Willingness to Pay,WTP)与受偿意愿(Willingness to Accept,WTA)作为影响地铁出行路径选择可观测因素的两种量纲统一化描述尺度，在交通系统服务水平评价及优化中扮演着重要的角色.例如，它们是交通系统利用“成本—效益”分析(Cost-benefit Analysis,CBA)和利用社会福利经济学(Welfare Economics)理论解决问题的重要输入参数，可将不同指标的量纲统一化，计算效益及福利变化.本文以行程时间属性为参照计算WTP 与WTA，即本文中的WTP 指旅客为使出行过程中某一属性变好所愿意多花费的行程时间，WTA指旅客因出行过程中某一属性变坏而期望减少的行程时间.根据前景理论，由于损失规避现象，旅客对于同一属性的WTP 与WTA 是不对称的[1].因此，考虑不对称性的WTP与WTA研究对地铁系统精细化管理有重要意义.

在理论研究方面，Hess 等[2]，De Borger 等[3]通过研究小汽车出行者的时间价值验证了不对称性的存在；Masiero 等[4]研究了不对称性对货物运输政策制定的影响；Liu 等[5]研究了不对称性对旅客决策行为的影响；朱海等[6]研究了异构模型对公共交通旅客时间价值求解的影响；Batarce 等[7]、房德威等[8]研究了地铁系统的拥挤成本.在实证研究方面，陈治亚等[9]与De Borger 等[10]将WTP 作为输入参数在社会福利经济学理论下研究了地铁票价优化策略，Björklund 等[11]研究了用于政策制定的公共交通拥挤成本.

总结发现，针对公共交通系统的支付意愿研究多集中于时间价值及拥挤成本，针对于地铁系统的研究与实证多未考虑WTP 与WTA 的不对称性，将他们等效处理，这种做法会导致优化与评价结果的偏差.鉴于此，结合成都地铁SP 调查数据，本文构建了多种地铁旅客路径选择异构模型，比较研究WTP与WTA的不对称性，以期为地铁系统服务水平优化与评价提供支撑.

1 调查数据

面向成都地铁开展SP 调查，依据《2018年中国城市通勤研究报告》中成都市出行距离的分布情况，调查问卷按照出行距离长度分为5，15，25 km，使用序列正交设计法生成调查问卷，每种调查问卷包含18 个场景，每个场景包含3 个无标签选择枝.国内地铁系统多采用区间计费，票价不影响地铁旅客路径选择行为，故本文未考虑票价因素.针对乘车舒适度属性，调查发现，旅客对于立席密度为6及以下的拥挤不敏感，当大于6时反应强烈；为保证研究属性的显著性，以立席密度大于6的车内时间表示乘车舒适度.为增强受访者代入感，将使用3DsMax渲染的地铁C型车立席密度为6 的情景图片插入调查问卷，如图1所示.采用基于真实水平的属性水平设置技术，结合成都地铁统计数据对试验情景下的水平值进行取值，属性设置及取值如表1所示.通过网络平台，面向成都市居民展开调查，最终获得有效问卷792 份，共计14 256 条有效决策.问卷统计结果如表2所示，数据结构基本符合成都市居民个人属性特征.

表1 SP 实验设计属性与水平设置Table1 Attributes explanations and levels in SP design

图1 C 型车内立席密度为6 时拥挤程度示意Fig.1 Schematic diagram of congestion in C-type car when passenger density is 6

2 支付及受偿意愿模型

WTP与WTA多基于非集计模型求解.非集计模型假设决策者在决策时会选择效用最大的选择枝，选择枝的可观测效用通过构造效用函数计算.在考虑不对称性时，计算WTA 与WTP，需构建考虑参考依赖的非线性效用函数，即将选择枝的各属性相对于参考点的增加值(inc)与减少值(dec)作为新的属性构建效用函数.诚然，WTP 与WTA 的不对称计算结果可能是由这种非线性效用函数导致的.为排除这种可能性并研究支付及受偿意愿的不对称性，本文将构建多种异构模型以对比分析.

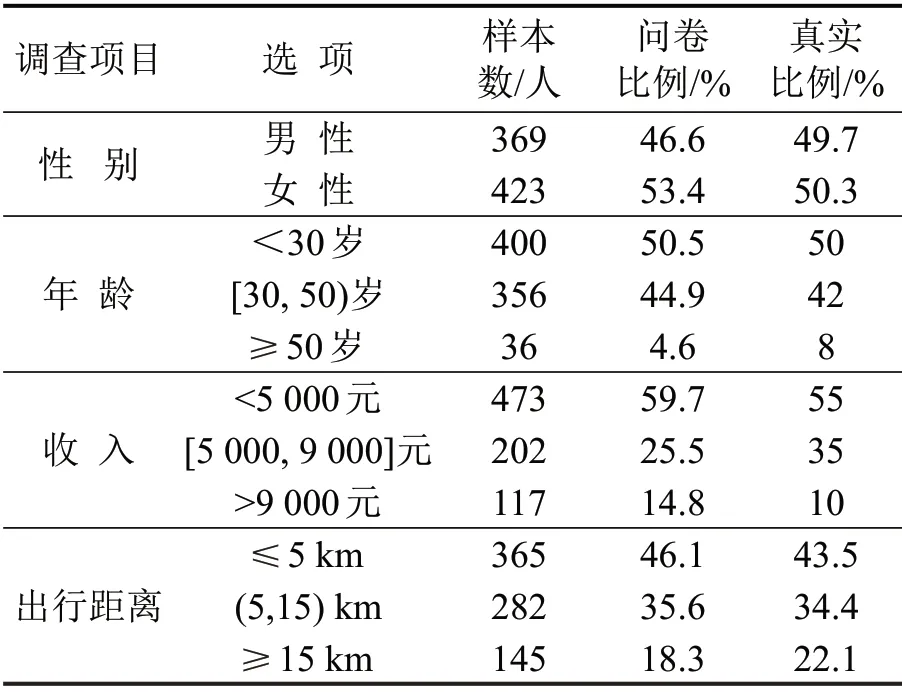
表2 受访者社会经济属性特征及出行结构Table2 SDC structure and travel structure of passengers in survey

2.1 异构模型

(1)对称同质偏好MNL模型.

情景s下选择枝j的可观察效用Vsj表示为

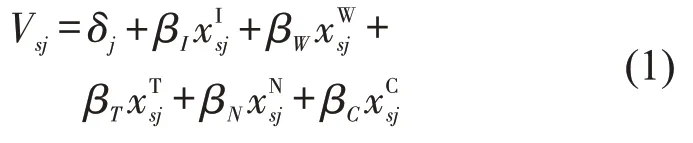
(2)不对称同质偏好MNL模型.

本模型中可观察效用Vsj表示为

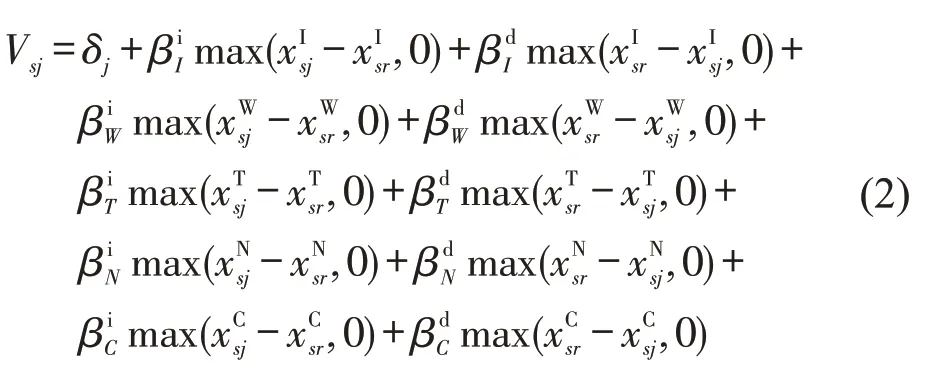
式中：xIsr、xWsr、xTsr、xNsr、xCsr分别为场景s各属性的参考点；βIi、βWi、βTi、βNi、βCi对应为各路径属性相对与参考点增加值的参数；对应为各路径属性相对与参考点减少值的参数.

(3)对称异质偏好ML模型及不对称异质偏好ML模型.

假 设βL=(βI,βW,βT,βN,βC)和服从连续型分布，则可基于MNL模型导出对称异质偏好ML模型及不对称异质偏好ML模型.

2.2 考虑不对称性的WTP与WTA求解方法

式中：βki，βkd分别指代越小越好因素相对与参考点增加、减小值的参数；βli，βld分别指代越大越好因素相对与参考点增加、减小值的参数.

根据不对称同质偏好MNL 模型标定结果，使用式(3)可求解越小越好的属性k总体水平的支付意愿Pk及受偿意愿Ak，使用式(4)求解越大越好的属性l的总体水平支付意愿Pl受偿意愿Al.

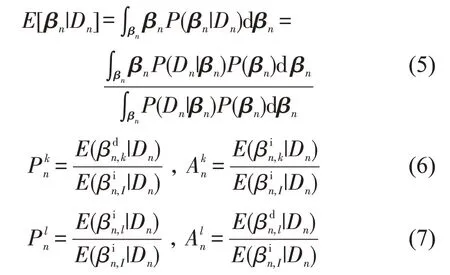
式中：，分别指代个体n的越小越好因素相对与参考点增加、减小值的参数；，分别指代个体n的越大越好因素相对与参考点增加、减小值的参数.

使用不对称异质偏好ML模型标定结果，求解各属性个体水平的WTP 与WTA 的方法为：首先，根据式(5)与个体n的观测数据Dn，估计个体n的所有属性增加值、减小值的对应参数其次，使用式(6)计算个体n越小越好的属性k的支付意愿Pn(k)，受偿意愿An(k)，使用式(7)计算个体n越大越好的属性l的支付意愿Pn(l)，受偿意愿An(l).

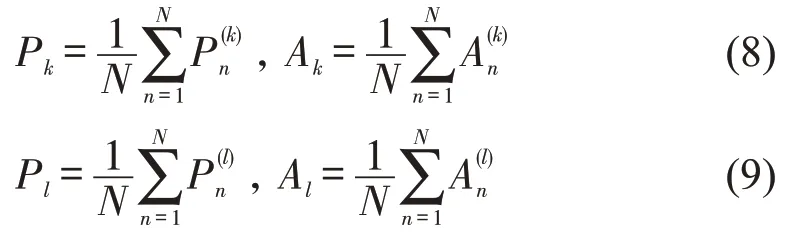
式中：N为受访者总人数.

使用不对称异质偏好MNL 模型标定结果，依据式(8)和式(9)可计算总体水平的WTP与WTA.

3 结果分析

3.1 模型设置与标定

决策者用于衡量损失与收益的参考点可分为内生参考点与外生参考点两种.外生参考点常在进行SP 调查的同时调查得到，内生参考点通过情景水平得到[12].本文将对比两种常用的内生参考点，即情景中各属性水平的中值(编号1)和情景中各属性水平的均值(编号2)分析不对称性.

根据2.1节建立12种异构模型如表3所示，模型3～7为βI、βW、βT、βN、βC具有不同参数分布结构假设的对称异质偏好ML，模型8～12 为βIi、βWi、βTi、βNi、βCi、βId、βWd、βTd、βNd、βCd具有不同参数分布结构假设的不对称异质偏好ML.

表3 异构模型编号及设置Table3 Number and settings of variation structure models

为比较模型解释能力，使用所有SP 数据标定模型1～12，并求解出极大对数似然估计值LL/SLL、拟合优度R2、赤池信息指数AIC/N，如表4所示，其中异质偏好ML 模型标定考虑受访者的连续选择.由表4发现：①在考虑不对称偏好后，MNL与及大部分ML模型的LL/SLL、R2及AIC/N均有显著改善，表明旅客在进行路径选择时存在损失规避现象，且参数分布假设对模型标定结果有显著影响.②相较于MNL模型，对称偏好ML模型及不对称偏好ML 模型的LL/SLL、R2及AIC/N改善显著，表明旅客在进行路径选择时个体间存在异质性.③以场景各属性均值为参考点，假设各参数服从对数正态分布的ML模型，相对与对称同质偏好MNL模型，在LL/SLL 方面提升了23.37%，在R2方面提升了60.72%，在AIC/N方面下降了22.77%，模型拟合效果改善显著，说明旅客在进行路径选择时不对称偏好和异质性同时存在.

为进一步验证模型的有效性，按出行距离比例，筛选70%的SP数据作为训练集，剩余数据作为测试集.使用训练集数据标定模型1～12，分别在两组数据集下计算预测精度(Percent Correctly Predicted)，如表5所示，方法见文献[13].对比表明，各模型在两组数据集下预测精度基本一致，且远高于文献[14]中对预测精度最小值的定义(机会估计准确率的125%)，即0.333%×1.25 ≈41.667% ，所以本文所构建的各异构模型是有效的.

3.2 个体水平分析

参考点2效果优于参考点1，模型12解释能力远劣于模型8～11，故对于不对称异质偏好模型，将只对使用参考点2标定的模型8～11的结果进行分析研究.根据1.2 节方法，计算个体水平各路径属性WTP 及WTA，并绘制累计频率分布图(CDF)如图2～图6所示.由于部分WTP及WTA分布尾部较长，部分价值区间累积频率未展示.

由CDF图像可得：①使用模型8、9、11求解的各路径属性WTA 及WTP 的CDF 形态相似，且各路径属性WTA 存在正值，WTP 存在负值；这与上述分布的拟合结果在区间( -∞，0 )或( 0,+∞)的概率不为0 有关.②从头尾部长度来看，(负)对数正态分布尾部最长，求解出的WTP异质性最强；截尾正态分布尾部最短，求解出的属性WTA 小于0 概率与属性WTP 大于0 概率均最大，说明分布假设对个体水平支付意愿求解有一定影响.③各属性WTA 较WTP 分布更集中，WTP 在受访群体间异质性更强，体现出两者在群体间异质性程度上存在不对称性.

表4 各参考点取值下异构模型标定测试统计量比较Table4 Comparisons on statistical criterions of variation structure models with different reference point

表5 异构模型训练集与测试集预测精度对比Table5 Compariations of percent correctly predicted of variation structure models

图2 行程时间WTAFig.2 WTA of incar time

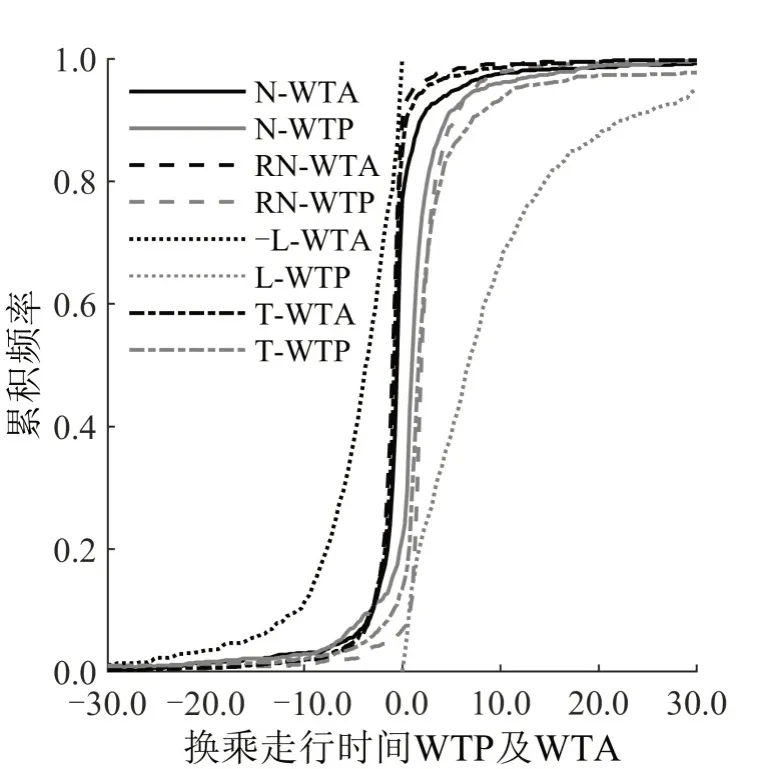
图3 换乘走行时间WTP 及WTAFig.3 WTP and WTA of transfer walk time

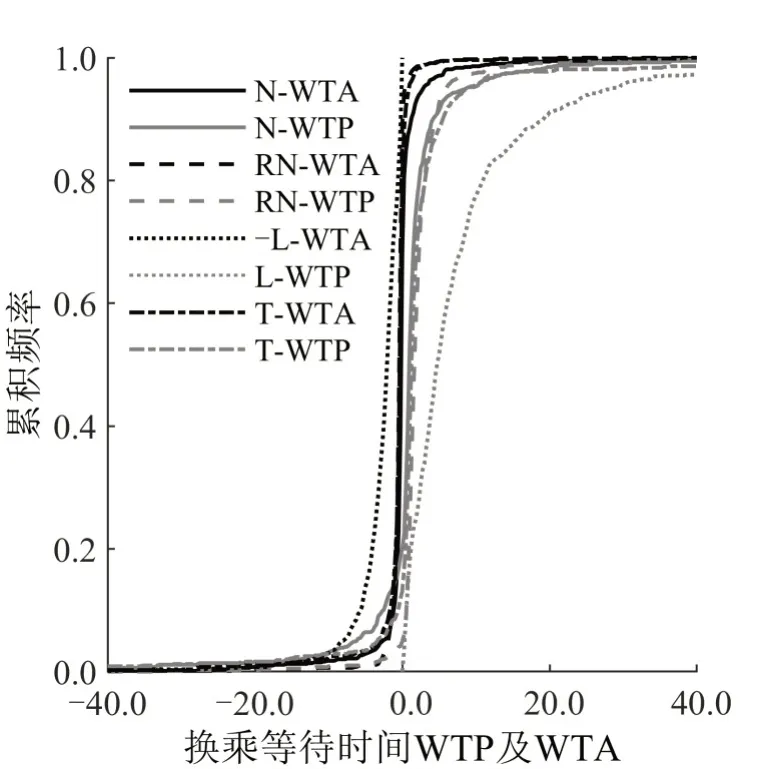
图4 换乘等待时间WTP 及WTAFig.4 WTP and WTA of transfer waiting time

图5 立席密度大于6 时车内时间WTP 及WTAFig.5 WTP and WTA of crowding time

图6 换乘次数WTP 及WTAFig.6 WTP and WTA of Transfer times

3.3 总体水平分析

根据2.2 节方法求解各模型的各属性总体水平WTP 与WTA，结果如表6所示.由表6可得：①模型2、8、9、11计算结果较为接近，模型10计算结果绝对值均高于上述模型，主要是因为模型系数的非负(正)假设，导致参照属性系数分布均值的绝对值显著小于其他属性参数，说明不对称异质偏好模型的参数分布假设对总体水平支付意愿求解有一定影响.②换乘走行时间、换乘等待时间、换乘次数及拥挤时间的WTA 小于0，换乘走行时间的WTP绝对值约为WTA的1.92倍，换乘等待时间的WTP 绝对值约为WTA 的2.32 倍，换乘次数的WTP 绝对值约为WTA 的6.34 倍，拥挤时间的WTP 绝对值约为WTA 的1.76 倍，车内时间的WTA 绝对值小于1，各属性总体水平受偿意愿皆小于支付意愿，说明总体水平的WTA与WTP在大小方面存在不对称性.

表6 样本总体WTA 及WTPTable6 WTA and WTP of overall level

4 结 论

本文依托成都地铁路径选择SP 问卷调查数据，对对称同质偏好、不对称同质偏好、不同连续分布假设下的对称异质偏好及不对称异质偏好模型进行了参数估计，考虑不对称性求解了以行程时间减少值为参照的个体水平及总体水平WTP与WTA.具体结论如下：

(1)对称异质偏好模型与不对称异质偏好模型结果显示，参数分布假设对模型标定结果和支付意愿求解结果影响明显；对于两种内生参考点，情景中属性水平的均值标定效果优于情景中属性水平的中值的效果.

(2)本文构建的模型中，以情景均值为参考点的不对称异质偏好模型在各标定测试统计量方面表现最好，说明该模型较其他模型能更准确地描述旅客的决策行为.以该模型标定结果求解所得的个体及总体水平支付与受偿意愿显示，相对于受偿意愿，支付意愿个体间的异质性更强，总体水平的绝对值更大.因此可以表明，支付与受偿意愿的不对称性在总体水平大小及个体间异质性方面皆有体现.

(3)总体水平的支付与受偿意愿在大小方面差别较大，如使用未考虑不对称性的非集计模型估计出的支付意愿进行实证分析，会导致社会福利或效益等目标的计算结果产生偏差.

(4)支付与受偿意愿在个体间异质性方面差别较大，在使用非集计模型预测地铁旅客路径选择行为时，应使用考虑损失规避现象及个体间异质性的模型.

利用AFC数据挖掘RP数据，以更加详细地表征路径特征，展开模型分析是进一步研究内容.