基于Epsilon约束法的高速铁路客票多目标定价研究

李雪梅，曹慧卓

(北京交通大学经济管理学院，北京100044)

0 引 言

高铁客票定价市场化改革备受社会关注.2015年12月，国家发展改革委员会下发《改革完善高铁动车组旅客票价政策的通知》，明确中国铁路总公司(下称“铁总”)对高铁的自主定价权.2017年4月，铁总上调东南沿海部分高铁车次的票价，2018年5月上调部分线路的高等级席别票价，同年7月在部分线路实行最大65%折扣的浮动票价.票价总体有升有降，涨价有利于增加企业利润，降价有利于增加旅客福利.可见，高铁客票定价要在增加企业利润和保障旅客福利的多目标中寻优.

高铁客票多目标定价研究主要有两种思路.一种是在多个单目标定价方案中择选，单目标定价方案是指企业根据唯一目标制定票价决策.如认为铁路峰值期宜根据社会福利目标定价，非峰值期宜根据利润目标定价[1]；或根据定价部门的需求对比不同目标的定价方案，如以收益、利润、出行量和社会福利作为定价目标[2].这种思路不涉及多目标间的权衡取舍，而是对比单一目标定价结果制定最优方案.另一种思路是多目标定价方案，即企业同时考虑多个目标制定票价决策，常见的有加权和方法和Epsilon 约束法.加权和方法是将每个目标赋权后的加和作为目标函数，如在航空与高铁竞争情形下，当高铁以利润和社会福利加权和为定价目标时，权重选取对票价制定的影响[3-4].已有多目标定价研究大多采用加权和方法，结果受制于主观的权重设置，且受限于目标问题的凸性.Epsilon 约束法是在某一目标的约束中考虑其他目标，保留目标间的对抗性，多目标的取舍相对客观，且对目标函数没有限制.Epsilon约束法形成后[5]，多用于交通规划领域，在高铁定价应用方面较少.本文选择Epsilon 约束法更适合求解高铁客票多目标定价问题.

本文研究问题是以企业利润和旅客福利为目标的高铁客票定价，在客运市场中考虑旅客差异和多种运输方式竞争，构建高铁客票多目标定价模型.双层规划模型刻画利益主体间的博弈关系，Epsilon 约束法建立目标间对抗关系，根据分层序列思想分解多目标问题，设计松弛算法得到纳什均衡解.根据解对应的目标值绘制近似的帕累托边界，以此确定多目标问题的最优决策.创新在于引入Epsilon约束法求解高铁客票多目标定价问题.

1 问题描述

高铁客票定价的直接利益主体是高铁运营方和旅客，双方根据决策目标进行博弈.高铁定价目标有运营方利润最大化和出行旅客福利最大化，决策结果是高铁票价.旅客以出行效用最大化为决策目标，决策结果是每种方式出行的人数.从客运市场的供给方看，多种运输方式存在竞争博弈，其他运输方式运营方是高铁客票定价的间接利益主体；从需求方看，旅客具有异质性.各利益主体经过动态博弈后形成稳定的纳什均衡解[6].由于多目标定价存在N个纳什均衡解，最优决策是在解集中借助帕累托边界(不能在不降低其他目标值的前提下增加某一目标值的解的集合)找到最优解，这也是本文研究难点，求解思路详见2.5 节.本文逻辑框架如图1所示.

图1 逻辑框架Fig.1 Logical framework

多种运输方式包括高铁、航空、高速客车及非公共交通(指私人小汽车或9 座以下乘用车)，前3种公共交通记作m=1,2,3，非公共交通记作m′.由于票价和时间是影响旅客出行因素中可量化且最主要的影响因素，大多研究将票价和时间作为区别异质性旅客的依据[7].据此，设计两种理想类型的旅客：时间敏感型和价格敏感型，分别记作k=b 和k=l，旅客特征由价格敏感度ξp,k和时间敏感度ξt,k体现.旅行时间对时间敏感型旅客的出行效用影响较大，表现为时间敏感度较高而价格敏感度较低，如以商务、通勤为目的的旅客；票价对价格敏感型旅客的出行效用影响较大，表现为价格敏感度较高而时间敏感度较低，如以旅行、休闲为目的的旅客.高铁运营部门可以通过购票时间对不同类型的旅客进行甄别.

2 模型构建

2.1 模型假设

(1)假设单位人次运营成本c(m)与旅客类型无关，仅与出行方式有关.

(2)假设旅客出行效用由确定效用和随机扰动项决定，互相独立并符合Gumbel分布.

2.2 旅客出行效用函数

公共交通方式的确定效用由票价、旅行时间和拥挤度构成.非公共交通方式的效用值为常量，在效用函数中添加常数项χk，=χk为固定常数，对于公共交通方式，χk=0.定义为

拥挤度可以表示为负载程度(出行量占容量B(m)的比例)的增函数，即

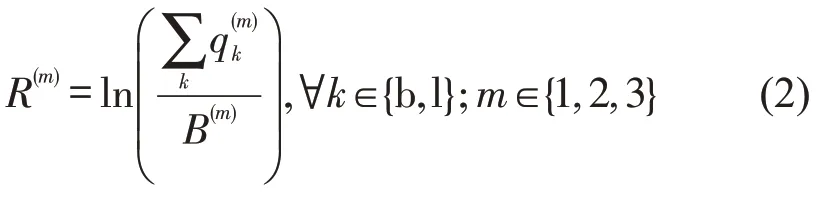
2.3 下层模型：旅客出行决策

双层规划模型刻画客运运营方与旅客之间的供需博弈，也可加入多种运输方式竞争博弈，上下层模型通过变量票价和出行量建立联动.下层模型确定旅客出行决策，公共出行分担率和非公共出行分担率用Logit模型表示为

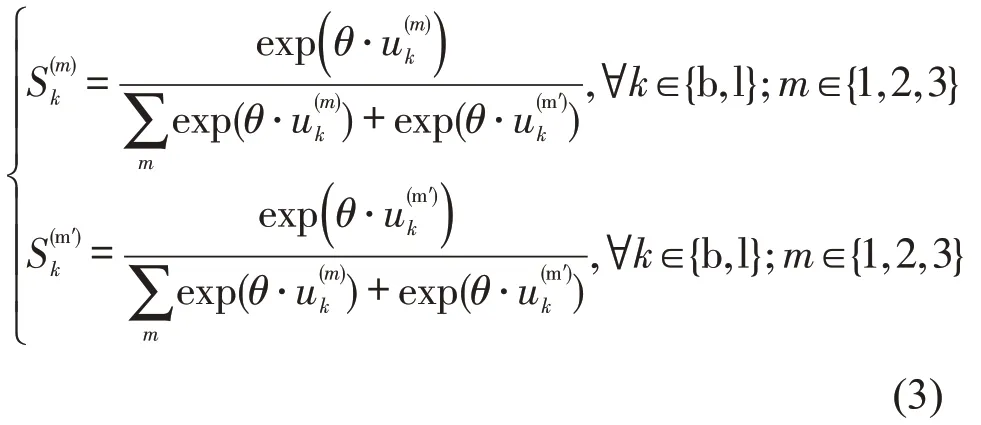
式中：θ为换算系数.

旅客出行量由分担率得到，下层模型约束为流量不得超过容量，下层模型为

式中：α表示公共交通出行量占客运总需求Q的比例；β表示时间敏感型旅客占公共出行量的比例.

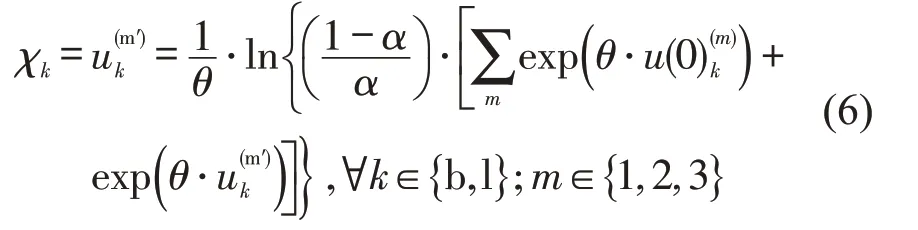
2.4 上层模型：票价决策

上层模型分别考虑运输企业各自的利润和整体旅客福利目标，确定票价决策.利润目标记为P，等于运营收入扣除运营成本，表示为

由于扰动项假设和出行的离散选择特征，个体旅客福利函数可表示为所有可选出行方式期望效用和的对数除以ξp,k[8].个体旅客福利与相应旅客人数相乘，即为整体旅客福利函数，记为PW，表示为

约束条件为票价不低于每人次运营成本，即

2.5 求解过程

多目标定价问题可根据分层序列思想进行分解[9].具体操作如表1所示：首先，求解单目标定价问题，即满足企业利润最大化(S1)或旅客福利最大化(S2)时的企业利润最大值π和旅客福利最大值σ；继而，求解多目标定价的最佳结果，将π或σ作为另一目标的约束值(Epsilon)引入模型，S3以企业利润最大为目标函数并保证旅客福利水平不低于σ，S4 以旅客福利最大为目标函数并保障企业利润水平不低于π，可得目标值上限；最后，求解多目标定价的最差结果，S5是将S3目标函数换乘企业利润最小，S6是将S4目标函数换成旅客福利最小化，可得目标值下限.S1，S4 和S6 优先满足企业利润，S2，S3和S5优先满足旅客福利.在目标值变动范围内均等选取Epsilon 值，作为π*和σ*替换S3和S4中的π和σ，将解所对应的两个目标值绘制于坐标系中，得到近似的帕累托边界，以此确定最优决策.

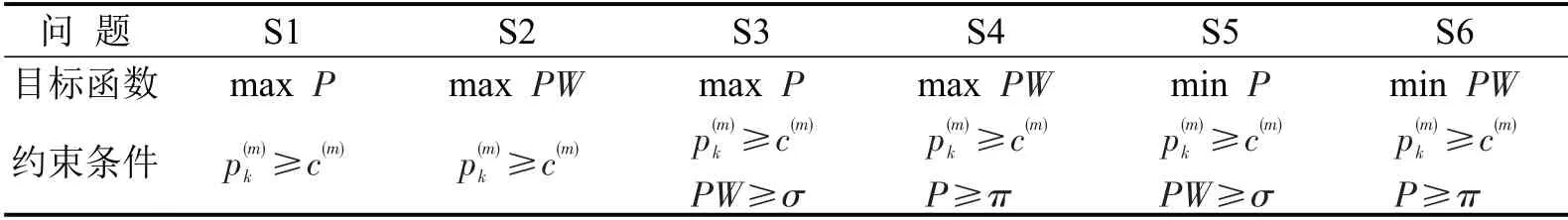
表1 多目标定价的分解问题Table1 Decomposition problem of multi-objective pricing

上述6个问题均采用松弛化算法寻求最优解，步骤如下：

Step 1初始化.

设置迭代次数t=0，将初始值，代入模型中.

Step 2求解下层模型.

当解满足容量约束，直接进入Step 3；否则采用权重方法，m∈{1,2,3}，得到符合容量约束的分流结果.

Step 3求解上层模型.

(1)初始化.设置迭代次数n=0，带入初始值，

(2)求解均衡票价.高铁的上层模型根据表1求解，航空和高速客车的上层模型分别根据式(7)和式(9)求解，结果记为.

Step 4更新结果.

3 算 例

长途旅行中，民航是高铁的主要竞争方式，短途旅行中，高速客车是高铁的主要竞争方式.为区别不同运距情境下的主要竞争方式，长途以北京—上海(1 318 km)为例，短途以南京—上海(295 km)为例.成本数据参考文献(高铁0.35元/(人⋅km)[10]，高速客车0.26元/(人⋅km)[11]，航空0.47元/(人⋅km)[10])设置运营成本.票价和客流量数据取自2017年1月4日官方订票网站(12306 和携程)，将航空票价的最低票价设置为价格敏感型旅客票价，最高票价为时间敏感型旅客票价，日均容量由频次和定员数相乘获得.客运总需求量为公共交通出行人数总和除以α.α和β为贴近实际的估计值，其他参数设置同文献[6]，如表2所示.最大迭代次数t=15.

3.1 优化结果分析

表3中3～6列展示了高铁票价、客流变动百分比，7～8列展示了高铁利润和旅客福利表现.首先，从目标值表现来看，S3 和S4 得到了帕累托解，且量价变动幅度较小；其次，从旅客类型来看，时间敏感型票价比价格敏感型票价变动幅度大，尤其在优先满足利润时表现更明显，优先满足旅客福利时两者差别不大，均接近成本票价；最后，从运距情境来看，短途票价涨幅大于长途票价，短途涨价对时间敏感型客流影响较小，对价格敏感型客流影响较大，长途涨价效果反之.

表4中2～5列和6～9列分别展示了航空和高速客车的票价、客流变动，10～11 列展示了企业利润表现.在竞争影响下，空铁票价差距缩小，长途航空票价降低，时间敏感型机票降幅大于价格敏感型机票，两者差距缩小；在高铁涨价客流降低时，航空客流有所增加，且时间敏感型客流增幅较多；当高铁以利润为优先满足目标时，此时航空利润较高，S6达到最大值.受高铁票价影响，短途客车票价上涨，时间敏感型票价涨幅高于价格敏感型票价；当高铁涨价客流降低时，客车客流增加，且价格敏感型客流增幅较多；当高铁以利润为优先满足目标时，此时高速客车利润较高，S6达到最大值.

表2 模型初值及参数取值Table2 Initial value and parameter value

表3 高铁优化结果Table3 Optimization results of HSR

表4 航空、高速客车优化结果Table4 Optimization results of airline and high-way bus

3.2 目标取舍的最优决策

相比单目标定价，3.1 节的优化结果显示多目标定价实现了帕累托改进.在多目标定价方法下，不同目标值对应的最优解有多个，需要进一步借助帕累托边界确定最优决策.不同运距情境下的最优决策点不同，但决策都是根据帕累托边界，下文仅以长途OD为例进行说明.

在S3～S6 得到的目标值范围内，将10 等分的值作为Epsilon 值，分别代入S3 和S4 求解.图2坐标轴为目标值变动百分比，图中点为多个均衡解，连接线为近似的帕累托边界，按斜率变化将帕累托边界划分为4 个区域.区域A，利润从0 增加到50%时，旅客福利下降了37%；曲线在区域B变缓，利润进一步增加30%时，旅客福利仅多降6%；在区域C 下降最快，利润增加10%时，旅客福利下降25%；曲线在区域D下降平缓，利润新增10%时，旅客福利降低5%.当高铁更看重利润回报时，降低10%利润是最优决策，此时利润保留较多而福利损失较少.当高铁更看重旅客福利时，降低50%利润是最优决策，此时福利保留较多而利润损失较少.当决策者无偏好时，20%降低利润是最优决策.帕累托边界提供了客观的最优决策点，结合决策者的主观偏好，确定最终的最优决策点.

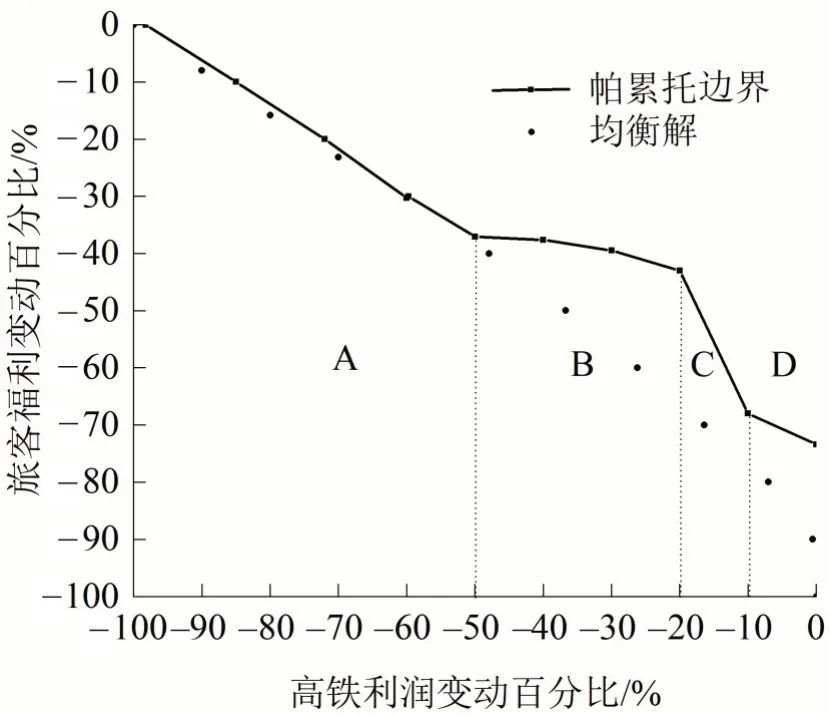
图2 帕累托边界Fig.2 Pareto frontier

4 结 论

以企业利润和旅客福利为高铁客票定价目标，考虑旅客差异和不同运距情境下的多种运输方式竞争，研究了高铁客票多目标定价问题.结合Epsilon 约束法构建了双层规划模型，根据分层序列思想分解多目标问题，设计松弛化算法求解.通过算例演示了多目标定价的最优决策，为高铁客票定价改革提供新思路.主要结论为：提出的多目标定价方法能够实现帕累托最优，对出行量、票价变动影响较小，有利于价改和市场稳定；就差别票价和运距情境而言，时间敏感型客票和短途客票有较高的涨价空间；市场竞争影响定价实施效果，高铁定价需关注竞争者策略；最优决策由帕累托边界和决策者的主观偏好确定.本文局限在于优化结果与特征参数等因素相关，后续研究可借鉴实证研究的参数取值，丰富旅客类型，在高铁网络中设计复杂的差别票价.