轨道交通网络级联失效影响范围研究

熊志华，姚智胜

(1.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京100044；2.北京市城市规划设计研究院，北京100045)

0 引 言

若轨道交通系统中某车站出现拥挤，会因网络化运营造成网络中其他车站相继出现拥挤，影响城市轨道交通系统的正常运营.研究轨道交通网络中拥挤传播规律，识别网络中拥挤传播范围，能为预防和控制轨道交通网络的相继故障提供理论基础，提高轨道交通系统的可靠性.

传染病模型和模拟仿真被大量用于轨道交通拥挤传播规律的研究.传统染病模型中传播速率和消散速率的量化，由于列车缺乏能力、站台滞留人数等与客流相关的参数不易直接获取，往往取定值，与实际有偏差[1-2].而微观仿真由于离散化的状态，宏观变量变化的描述适用性比较差，如采用元胞自动机，其格子数取值大，高效的计算能力易被抵消，且各参数离散化，观察随参数变化的系统行为较难.耦合映像格子(Coupled Map Lattice，CML)模型是一种将时间域和空间域离散化，但状态域仍保持连续的动力学系统，被广泛用于研究不同网络拓扑结构的相继故障行为，同时在城市道路网、公共交通网络及轨道交通网络的相继故障研究中得到应用[3-6].

现有的CML 模型在交通领域的应用大多是从网络物理层面分析其相继故障，即考虑网络节点间的连接关系.然而，CML 模型构建的过程中，时空离散化可能忽略小扰动，引起系统行为极大的偏差，故有必要探讨模型构建过程中的参数选取，如初始值和耦合系数.现有研究通常在(0,1)范围内随机生成网络节点的初始状态值[5]，耦合系数ε假定[5-7]，只获得相继故障规模，未确定相继故障的具体影响范围[4-6].本文立足于此，分析轨道交通拥挤传播机理，结合轨道交通网络特征和客流特征分析相应的CML 模型中的参数，给出路网失效传播范围的算法流程，通过仿真实例分析参数对轨道交通系统拥挤传播的影响，并界定网络拥挤范围.

1 拥挤传播规律分析

轨道交通客流从有序稳定状态演化为无序状态在网络上传播，主要表现为地铁车辆满载，后续车站乘客无法上车，大量客流滞留站台，后续车站也产生客流拥挤、积压，拥挤状态在站间传播，其中拥挤传播根本原因是客流连续和列车间隔发车造成的[7].假设xk是节点k的交通状态，xk-1是上游节点k-1 的交通状态，站点k进站客流Ik和换乘客流Hk决定了车站候车客流量Pk；而上游断面客流、车辆的运输能力、发车间隔、本站出站客流Ok、换乘客流Hk决定了车辆的剩余载客能力Qk，上游断面客流是由上游的交通状态xk-1决定，车辆的运输能力、发车间隔一般都是确定的.Uk=f(Ik,Ok,Hk)表示是当前节点进出站客流、换乘客流等函数关系.节点k的交通状态由上游节点的交通状态及当前节点自身特性决定，有xk=Z(Uk,xk-1),k=1,2,…,n，n表示节点数，假设第k个节点拥挤的临界状态是，根据泰勒展开可以得到

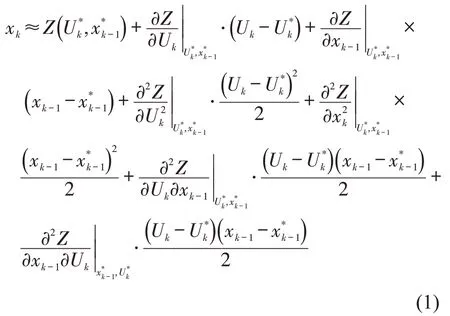
令：

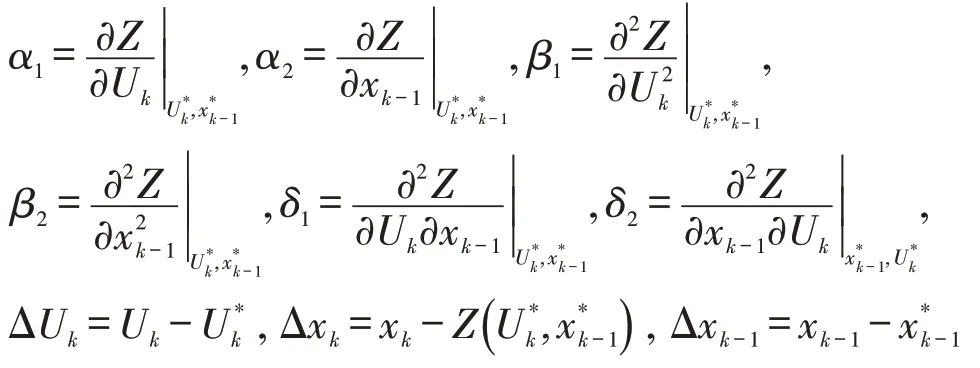
式(1)可以变换为

上游站点交通状态与下游站点自身特性相互独立，可近似认为

式(3)表明当前站点交通状态的波动与上游节点交通状态波动及本站点自身客流波动的关系.拥挤传播在空间维度表示上下游关联，站点之间的影响是累积的，可以推算.其中，Var 表示站点交通状态值的方差，i代表与节点k-1 有关联的节点集合，m表示第i个节点自身的影响因素集合，r表示站点自身第r个影响因素.本站自身客流波动因素包括本站进站客流，上游列车到达本站的下车客流，线路间换乘客流.

通过上述拥挤传播机理分析可知：轨道交通拥挤传播受网络物理结构，进出站、换乘客流和初始交通状态影响；拥挤传播也随时间不断推移，函数Z(Uk,xk-1)要考虑时间维度.因此，本文在传统CML模型中，融合随时空变化的节点初始状态、耦合系数，将网络的物理结构、客流条件及初始交通状态融合进模型中.

2 基于拥挤传播机理的模型构建

CML 是一种半宏观描述时空系统的模型，节点初始状态xi(t)，即t时刻节点i的状态函数，是随时间变化的值，节点间的权重为

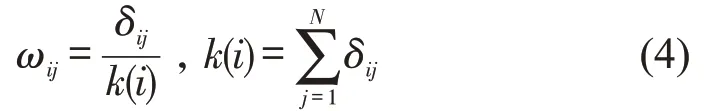
式中：ωij为节点i和节点j之间的权重；k(i)为节点i的度，表示节点i有几条边相连；δij为轨道交通网络的连接系数，若节点i和节点j相连δij=1，否则δij=0；N为节点数.

映射函数选择Logistic映射方程，即

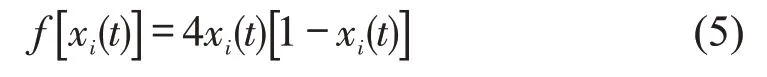
轨道交通客流拥挤传播模型为

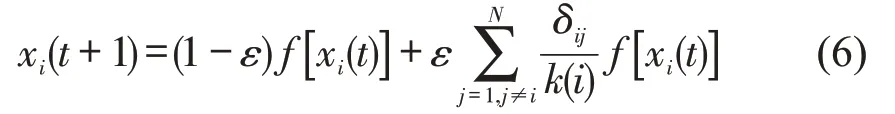
式中：ε是耦合系数，表示各节点之间的相关系数，值越大，节点间关联越紧密，ε∈(0,1).

由于轨道交通拥挤传播受网络的物理结构、客流条件及初始交通状态影响，站点的交通状态、客流条件是时变的，而CML 模型对初值敏感依赖，很小的扰动可能对状态的变化有很大的影响.t时刻格子点i受其邻近格点的作用，其状态由xi(t)变为xi(t+1)，格点i由0时刻初始状态x0(i)演变的序列为{xi(0),xi(1),xi(2),…,xi(t),xi(t+1),…} .随着连续迭代次数的不断增加，节点状态的误差会随之急剧增大.以往采取随机数作为初值具有不确定性，本文在传统CML 模型基础上，融合随时空变化的节点初始状态、耦合系数，减少误差的传播.

取列车的满载率作为节点的初始值，即Vi(t)/Ci(t)，其中，Vi(t)为节点i上游列车在t时刻的断面客流量，Ci(t)表示节点i上游列车在t时刻的运能，一般某一线路为定值CL，不同线路L取值不一定相等.一旦满载率取值接近1，说明可能开始出现拥挤.

耦合系数ε以往采用定值，整个网络取值一样，忽略了节点间的差异性，为掌握节点耦合关系，根据历史数据拟合，获取路网的耦合强度系数εi为

耦合系数可能会超过1，通过0-1 变换使得耦合系数在(0,1)之间.根据客流数据，拟合各个节点之间的耦合系数，针对不同扰动发生时刻，耦合系数也是时变的.每个节点与其他节点之间的耦合系数不仅与网络的拓扑结构相关，而且与相连线路满载率相关.

3 CML模型的量化

以某轨道交通网络为例，如图1所示，选取4条线路中60 个车站的实测数据，统计某星期一每隔30 min 的客流量数据，以此为基础量化模型中参数.

将各条线路的满载率与上游车站属性相关联，作为网络中初始值，车站的满载率是随时间变化的.以30 min为时段，将02：00-24：00按顺序划分为44组时间序列，作为Y轴时间间隔坐标.图2显示，前往每一个车站的列车满载率有较大差异，高峰期07：00-09：00(序号11～14)和17：00-19：00(序号31～34)期间，满载率较大，与采用正态分布随机取值相比，能更好地结合网络客流特征，初始值更可靠，更符合实际.

图1 某轨道交通网络示意图Fig.1 An example of rail transit network

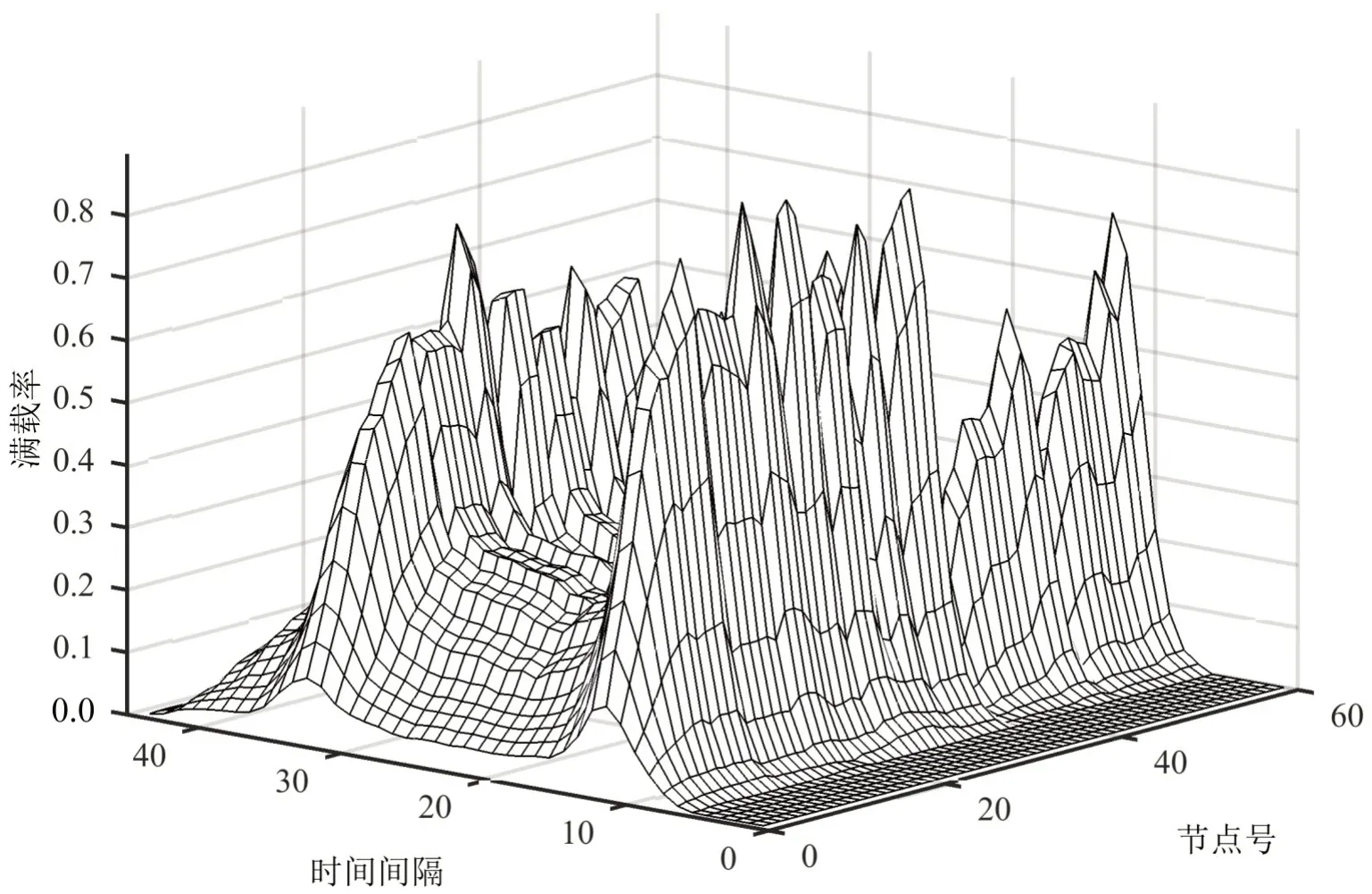
图2 车站间线路满载率变化图Fig.2 Ratio of passenger flow and capacity

分析轨道交通网络拥挤传播规律的算法流程如下：

(1)将实际的轨道交通网络车站映射为复杂网络中的节点，将线路映射为复杂网络中的边，构建轨道交通网络图.

(2)生成连接矩阵A=(δij)N×N，并计算节点i的度k(i),i=1,…,N，N为节点数.

(3)所有节点一开始都处于正常状态，测度整个轨道网络中的初始满载率作为各节点的初始值.

(4)当某一时刻T，某节点b出现故障或失效，此时节点b的状态变量加上一个扰动，在此后所有时刻，节点b的状态函数设为0，标记为拥挤节点.

(5)对每个节点，按照耦合映像格子更新其状态，如果xi(t)≥1，则节点i受到节点b影响变为拥挤状态，标记节点为故障点，并继续更新其余节点的状态值.

(6)若网络中所有节点均满足xi(T)＜1，则网络拥挤的影响范围终止.

4 实例验证

根据上述网络和算法，设定3 种情景.情景1假设初始值未知，采用蒙特卡洛法模拟3 000 次，取平均值观察初值变化对结果的影响，初始值和耦合系数都假定在(0,1)范围内取值；情景2假设初值已知，探讨不同时段和不同的耦合系数拥挤传播的范围；情景3根据实测的客流量量化的初始值和利用历史数据拟合的耦合系数，分析在真实网络运行状态下，拥挤传播的规律.

情景1 的初始值是随机生成(0,1)之间的正态分布函数值，由于初始值是随机变化的，假设节点17 发生扰动，耦合系数为0.5，每次仿真后在上述网络中传播的范围是随机变化的，如图3(a)所示，图中的直方图是频数，曲线是频数正态分布拟合曲线.由于初始值的变化，导致每次计算的拥挤车站数差异很大，有时拥挤车站数为30，有时拥挤车站数为2，而不同时刻拥挤车站数的差异又会影响下一时刻传播的范围.因此，初始值的选取对研究轨道交通拥挤传播范围影响很大.图3(b)是仿真多次后取均值描述不同耦合系数下拥挤传播范围.从图中可以看出，耦合系数较小时，拥挤几乎不传播，经过很短的时间，系统就恢复稳定状态；而耦合系数较大时，影响的车站数较多，需要经过较长时间系统才能达到一个稳定状态.这与传染病模型描述拥挤传播类似，只能估计规模，无法给出具体哪些车站受到影响.

图3 情景1 模拟结果Fig.3 Simulation results of scene 1

图4 情景2 模拟结果Fig.4 Simulation results of scene 2

情景2 通过观测轨道交通系统运营状态，获取车站上游列车满载率来描述相应节点的初始值，满载率是时变的，假设因节点17 发生扰动引发轨道交通系统相继故障随时间变化情况如图4(a)所示，Y轴表示时间序号，以30 min为时段，将02：00-24：00按顺序划分为44组时间序号.不同时刻由于初始值不同，影响范围差异较大.08：00-08：30(序号13)这一时段，其影响范围显著高于其他时刻，随着仿真时刻的推进，其影响范围不断扩大，直至稳定.晚高峰17：00-19：00 (序号31～34)影响范围显著高于相邻其他时段，在较短的仿真间隔内快速达到稳定.不同耦合系数下，在高峰时段(序号13)对网络拥挤传播的影响如图4(b)所示，耦合系数越大，拥挤传播的范围越大，传播的越快，与情景1类似，两者差别在于情景2给定了初始值，不再随机变化，反映的是更接近实际的状态而不是一种平均状态.

情景3 以实际的运营数据为基础，根据式(5)和图2可知，时空变化的满载率和耦合系数.以时间08：00-08：30(序号13)这一时段为例，不同站点满载率和站点间耦合系数不同，但取值确定.此时节点17发生扰动，拥挤的传播规律如图5所示.粗黑线覆盖的范围为节点17 在08：00-08：30 发生扰动时，由于网络的耦合作用传播至相邻车站，最终达到稳定时，网络受影响的范围.从图中可以看出，拥挤在网络中并不是均匀传播的，不同线路上，节点17发生扰动时产生的拥挤在站点间传播范围并不一致，这是由于各站点初始值、耦合系数的共同作用影响并不均匀，与客流分布有很大关系，体现了量化模型初始值和耦合系数的必要性.

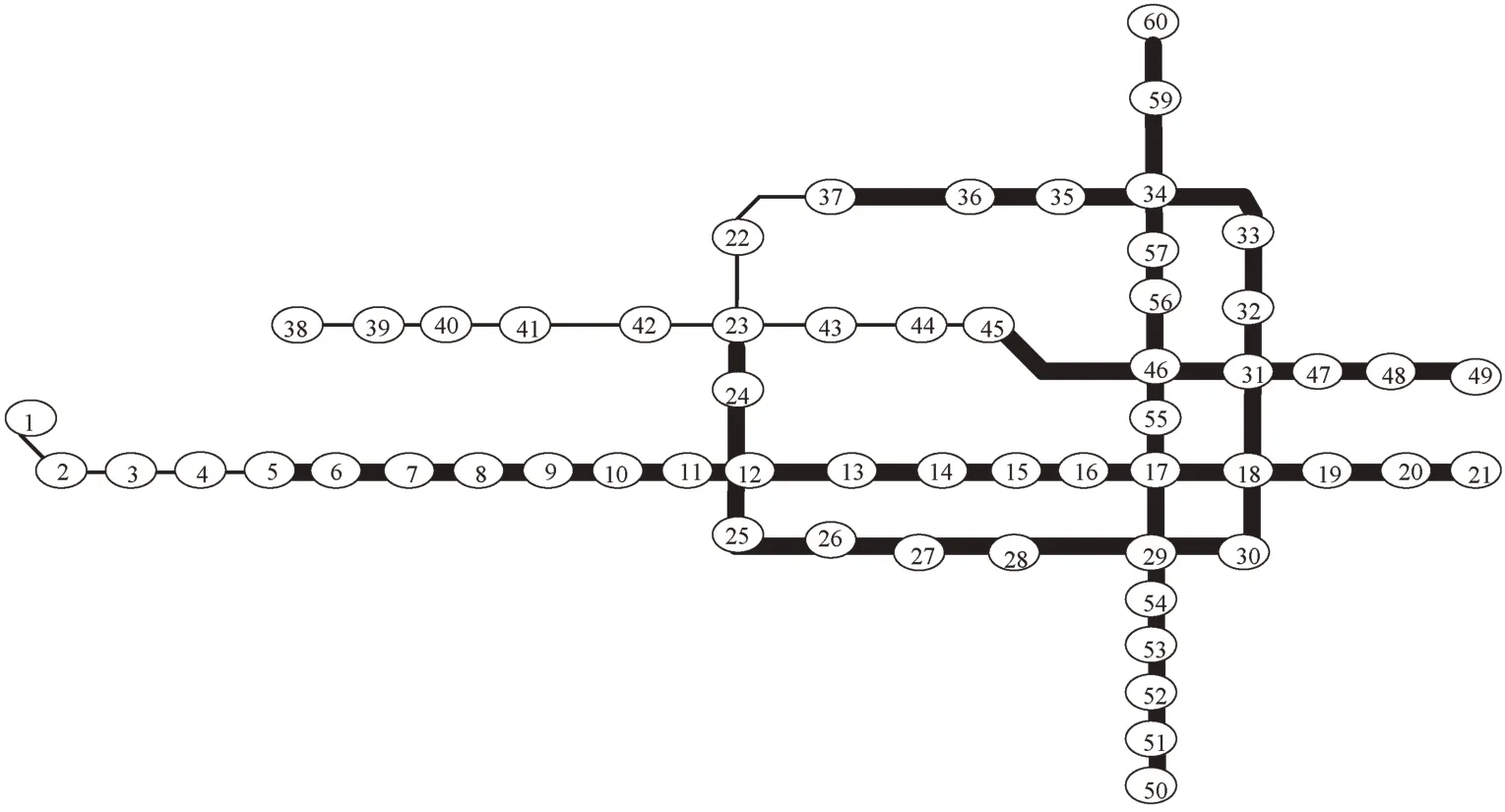
图5 情景3 拥挤传播范围示意图Fig.5 Range of congestion propagation under scene 3

具体传播过程如图6(a)所示，随着仿真时间的推移，在某一时段，如08：00-08：30(序号13)，拥挤车站先增加，然后逐步稳定；另一方面，不同初始时刻，拥挤传播范围变化也不相同，高峰期拥挤传播显著，而平峰期，拥挤传播不显著.此时考虑的是拥挤发生时，轨道交通网络的初始状态及耦合系数的时空差异性.

不同节点度k(i)的节点i发生扰动时，传播的范围会有所不同，如图6所示.17 号节点的节点度k(17)=4，43号节点的节点度k(43)=2.不同时刻17号节点发生扰动时，拥挤传播范围如图6(a)所示；43 号节点发生扰动，其传播范围如图6(b)所示.由于不同节点的初始值和耦合系数都不一样，并不具备可比性，在早高峰期，不同节点度发生故障传播范围差距不大，而晚高峰期节点度2的故障传播范围显著下降，这不仅与节点度相关，也与网络中的客流有关系.对于17号节点，其拥挤传播范围随着时间变化的趋势与情景2(图4(a))相比有显著的不同，主要体现在任意时刻节点都具有确定的初始值和耦合系数，在早晚高峰都具有显著的传播特性；而情景2中，晚高峰的传播性明显被低估了.情景3中耦合系数通过历史值拟合而成，表明轨道交通系统中节点间的耦合作用，不仅仅受网络的物理结构影响，也受车站间客流相互作用的影响.

图6 不同节点度不同时刻的拥挤传播范围Fig.6 Range of congestion propagation with different

通过上述3 种情景分析可以看出：传统CML模型，由于不考虑初始值影响，与以往的SIR 模型类似，考虑网络的拓扑结构，一旦发生相继故障，估计的是网络的一种平均状态；以满载率作为初始值的CML 模型，能较好地减少模型自身的扰动，但由于耦合系数采用定值，对站点间耦合强度估计不准确，弱化了不同站点间的差异性；时空变化的初始值和耦合系数确定的CML 模型能较好地反映实际网络状况，确定的相继故障范围更符合实际，并且能具体给出影响的车站位置，有利于制定应急预案.

5 结 论

轨道交通系统某一车站出现拥堵，因网络效应会引发相邻车站的相继拥堵，本文通过CML 模型研究这一网络相继故障现象.通过客流量化CML 模型中的初始值和耦合系数，与以往模型相比，减少了模型自身的扰动，更接近实际.同时考虑了初始状态、耦合系数和物理结构的CML 模型，可以评估拥挤传播影响范围，有助于及时确定应急管理范围，提前做好应急预案.由于客流具有随机性，关于客流影响的稳定性需要进一步研究.