基于比功率的自动驾驶交通流油耗分析
2020-02-28秦严严何兆益
秦严严,王 昊,何兆益,冉 斌
(1.重庆交通大学交通运输学院,重庆400074;2.东南大学城市智能交通江苏省重点实验室,南京210096;3.威斯康星大学麦迪逊分校土木与环境工程系,威斯康星州麦迪逊53706,美国)
0 引 言
近年来车辆尾气排放污染愈发严重,据统计[1],车辆尾气中NOx的排放量约占整个交通运输行业产生NOx排放总量的91.6%.车辆油耗与尾气排放和能源消耗直接相关,车辆油耗分析的相关研究日益受到关注[2].自动驾驶车辆的发展为减少车辆油耗提供了途径,在大规模自动驾驶交通流出现之前,探究自动驾驶车辆对油耗的影响具有前瞻性的现实意义.
针对自动驾驶车辆油耗影响的研究大致可分为两个方面:一方面是从优化控制的角度,提出以油耗降低为优化目标的自动驾驶纵向控制策略[3];另一方面是从交通流运营与管理的角度,应用交通流模型仿真分析自动驾驶交通流对油耗的影响[4].本文关注第二个方面的研究,其成果主要为不同交通场景及各种自动驾驶运行参数下的油耗影响结果,普遍认为自动驾驶车辆有利于油耗的降低,区别在于油耗降低的幅度有所不同.该类研究的开展仍不够充分,油耗作为一种交通流特性,与通行能力、交通安全等属于交通流的外在表征属性,而交通流稳定性作为交通流内在固有属性,与交通运营质量直接相关,故油耗特性的影响结果与交通流稳定性之间的内在关联性值得研究.对于传统交通流,有研究表明,交通流平稳性与拥堵缓解之间存在定性的影响关系[5];对于自动驾驶交通流,有研究分析了自动驾驶舒适性与稳定性之间的内在影响关系[6].但鲜有文献探究自动驾驶交通流油耗影响与交通流平稳性之间的关联性,鉴于此,本文通过数值仿真与理论分析相结合的方法,对此开展研究.
1 比功率油耗模型
相关研究表明[7-8],车辆油耗与发动机输出功率直接相关,而发动机输出功率与车辆瞬时速度及加速度相关.机动车比功率可较好地体现车辆微观轨迹数据(速度与加速度)与油耗之间的关系,成为评价油耗影响的基础模型.小汽车在平坦道路上行驶时的比功率[9]为
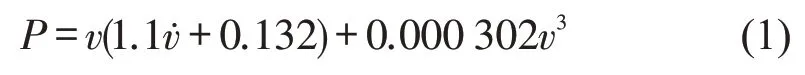
式中:P表示机动车比功率;v为车辆瞬时速度;为车辆瞬时加速度.
为建立车辆平均油耗率的数学模型,Song等[9]首先对P进行了区间划分,以消除逐秒数据的随机误差,即

式中:n为整数.
进一步地,Song等[9]建立了油耗率PFR的数学模型,即

则平均油耗率PAFR[9]为

式中:i表示P的第i个区间;PFRi为P区间i下的油耗率;Ti为车辆处于P区间i的时间长度.
因此,由式(1)~式(4),依据车辆微观轨迹的速度与加速度,便可计算平均油耗率,进而对油耗影响进行相关分析.
2 跟驰模型及稳定性
2.1 跟驰模型
对于手动驾驶,学者们提出了诸多跟驰模型,模型之间各有优劣,本文选择应用广泛的优化速度模型[10](Optimal Velocity Model,OVM),同时考虑驾驶人的反应延时,建立手动驾驶车辆跟驰模型为
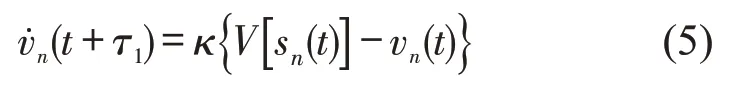
式中:为车辆n在t+τ1时刻的加速度;τ1为驾驶人反应延时;κ为敏感系数;sn(t)为车辆n在t时刻与前车的车间距;vn(t)为车辆n在t时刻的速度;V[sn(t)] 表示优化速度函数,公式为

式中:v0为自由流速度;s0为最小停车间距;α为敏感系数.
在常规跟驰模型的基础上添加多前车信息反馈是自动驾驶车辆跟驰模型常见的建模方式.依据文献[11-12],自动驾驶车辆电子节气门角度的上层控制系统与自动驾驶纵向控制系统的输出速度和加速度之间模型关系为
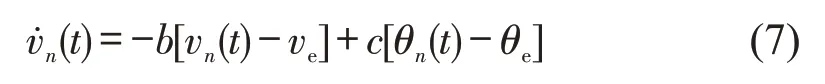
式中:b,c为系数;ve为平衡态速度;θn(t)为车辆n在t时刻的电子节气门角度;θe为自动驾驶车辆上层控制系统保持平衡态速度ve所需要的电子节气门上层控制角度.
可由式(7)计算自动驾驶车辆n与其前方车辆n-j的电子节气门上层输出的角度差为

由式(8)看出,文献[11-12]中自动驾驶车辆电子节气门上层角度控制可由上层控制系统输出的速度差与加速度差体现.依据文献[11-12],将式(8)作为自动驾驶车辆的前车反馈项,并考虑车间通信延时,建立自动驾驶车辆跟驰模型为

式中:τ2为自动驾驶车辆的车间通信延时;m为自动驾驶车辆多前车反馈的数量;wj为第j个反馈系数.
依据文献[13],手动驾驶员反应延时平均约1.2 s,自动驾驶的车间通信延时约0.4~0.8 s[14],OVM 模型参数如表1所示.鉴于自动驾驶车间通信可在4辆车之间有效传递[16],选取自动驾驶车辆多前车反馈数量为3,并依据文献[11]对前车反馈系数取值的研究结果,选取反馈系数取值依次为w1=0.35,w2=0.25,w3=0.15.

表1 跟驰模型的参数取值[1 5]Table1 Parameter values of car-following model
2.2 稳定性解析
应用李雅普诺夫方法分析手动驾驶车辆与自动驾驶车辆跟驰模型的稳定性.设车辆n在t时刻的平衡态位移为(t),则相对于实际位移xn(t)的扰动项rn(t)为

对式(10)求一阶和二阶导数,可得

对式(9)进行一阶泰勒展开,并将式(10)和式(11)带入,得到
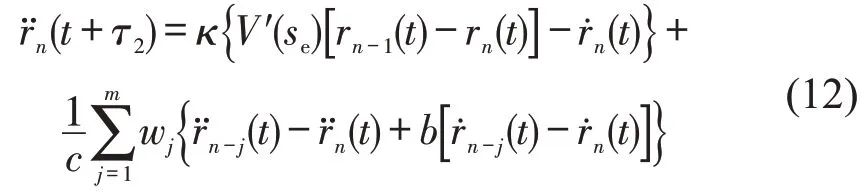
式中:se为平衡态车间距;V′(se)为优化速度函数关于平衡态车头间距的导数.
将式(12)转换为一阶差分方程,即
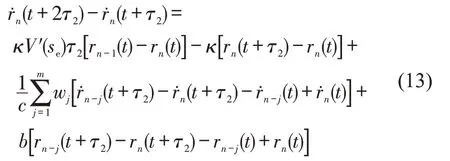
将扰动rn(t)写为傅里叶形式,即rn(t)=Aexp(iαkn+zt),并带入式(13),得到
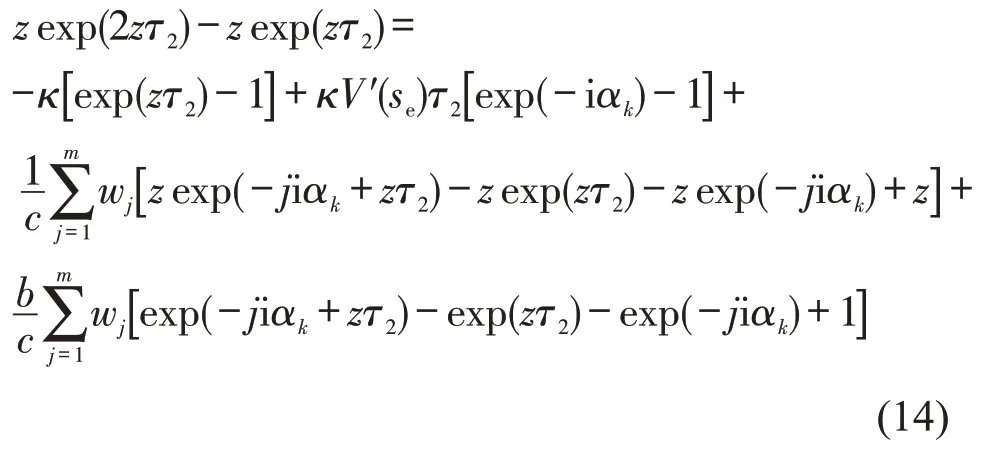
式中:αk为虚数系数;z为傅里叶变换系数;z1为一次项系数;z2为二次项系数.令z=z1(iαk)+z2(iαk)2+…,并带入式(14),计算(iαk)的平方项系数z2为

根据李雅普诺夫稳定性判别准则:若z2>0,则交通流稳定;反之,不稳定.令z2>0,化简得到自动驾驶车辆交通流稳定条件为

同理,可推导得到手动驾驶车辆交通流稳定条件为
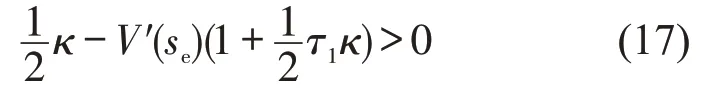
由式(16)和式(17)可以看出,在模型参数取值确定时,稳定性判别条件与V′(se)呈线性关系.根据式(6)可计算得到V′(se)与平衡态速度ve的关系为

由式(18)可知,V′(se)与平衡态速度ve也呈线性关系,故稳定性判别条件与平衡态速度ve应呈线性关系.将自动驾驶车辆与手动驾驶车辆的跟驰模型参数分别带入稳定性判别条件式(16)和式(17),计算得到两种车型交通流稳定性情况,如图1所示.图1中曲线的含义为稳定性判别条件:曲线值大于0表示对应的初始速度下交通流稳定;反之,不稳定.

图1 稳定性结果Fig.1 Stability results
由图1可以看出,手动驾驶车辆在0.0~24.9 m·s-1的速度范围内不稳定,在24.9~33.0 m·s-1的速度范围内稳定.而自动驾驶车辆在车间通信延时分别为0.4,0.6,0.8 s时,均可在自由流速度范围内稳定.
3 油耗影响分析
数值仿真实验是诸多交通流特性分析的常用方法[17],基于手动驾驶车辆及自动驾驶车辆跟驰模型的数值仿真可获取车辆微观轨迹数据,进而应用油耗评价模型,分析自动驾驶车辆对油耗的影响.
交通震荡是一种常见的交通现象,是指车辆速度出现反复加速与减速,以致形成时走时停交通流,进而易诱发交通拥堵.相关研究表明手动驾驶车辆在交通震荡下的油耗较大[18],故本文通过数值仿真实验模拟交通震荡,对自动驾驶车辆在交通震荡下的油耗影响进行分析.依据文献[19],周期性扰动仿真实验可较好地模拟交通震荡,在周期性扰动实验中,车队头车通过周期性地加减速形成周期性扰动,且扰动向车队上游车辆传播.具体[19]为:车队在初始时刻保持恒定的速度行驶,然后头车在第51~100 s 间以4 s 为周期,进行周期性地加减速,加减速度均为1 m·s-2,在第100 s之后,头车重新保持初始状态下的速度.
分别选择手动驾驶车队与自动驾驶车队经历上述头车的周期性扰动,进行周期性数值仿真实验.数值仿真实验基于MATLAB软件,应用常规驾驶车辆与自动驾驶车辆的跟驰模型进行数值仿真,获得手动驾驶车队与自动驾驶车队在交通震荡下的微观仿真数据,进行油耗影响分析.根据第1节比功率油耗模型,平均油耗率与车辆速度直接相关,因此,不同的车队初始速度将直接影响油耗的仿真结果.为了考察车队在不同初始速度下的油耗影响,数值仿真实验中,车队初始速度以0.1 m·s-1为间隔从1 m·s-1依次选取至33 m·s-1,并分别进行数值仿真实验,统计得到相应的平均油耗率,仿真中的仿真步长为0.1 s,统计油耗率的时间间隔为1 s.同时,车队数量从1 选取至30,作为参数敏感性分析,这样在自动驾驶车队中,从第4辆自动驾驶车辆开始才能全部接收其前方3 辆车的反馈信息.此外,自动驾驶车辆的车间通信延时τ2分别选为0.4,0.6,0.8 s进行参数敏感性分析.以统计得到的手动驾驶车队平均油耗率为基准,计算相同条件下自动驾驶车队平均油耗率相比于手动驾驶平均油耗率的降低百分比,作为油耗影响的仿真结果,如图2所示.
图2给出了自动驾驶车辆车间通信延时τ2分别选为0.4,0.6,0.8 s时平均油耗率的降低百分比,其中,横轴表示车队初始速度,纵轴表示车队中的车辆数,图中颜色表示相应车队初始速度与车辆数下,自动驾驶车队相比于手动驾驶车队平均油耗率的降低百分比.依据仿真结果计算可知,当τ2分别取0.4,0.6,0.8 s时,平均油耗率的降低范围分别在0.012 9%~60.389 4%,0.012 7%~60.361 0%,0.004 4%~59.945 9%,表明平均油耗率的降低幅度基本不受τ2取值的影响.同时可以明显地看出:当车队初始速度约小于22.5 m·s-1时(图中虚线),平均油耗率可大幅降低;相反,当车队初始速度约大于22.5 m·s-1时,平均油耗率的降低并不显著.说明自动驾驶车队相对于手动驾驶车队的油耗降低幅度与车队初始速度有关,而车队初始速度与交通流稳定性存在理论上的决定关系,因此,为了探究交通流稳定性是否与油耗降低存在定性的影响关系,对手动驾驶车辆与自动驾驶车辆的稳定性进行理论解析.

图2 平均油耗率降低百分比Fig.2 Average reduction percentage of fuel consumption
对照图1中自动驾驶与手动驾驶交通流稳定性结果可知,自动驾驶对手动驾驶油耗的降低幅度与稳定性状态的改变之间存在定性的影响关系,即在手动驾驶交通流不稳定性的速度范围,自动驾驶将手动驾驶的不稳定交通流转变为稳定状态,有利于显著降低平均油耗率.而在手动驾驶交通流稳定的速度范围,自动驾驶交通流同样的稳定状态使得平均油耗率的降低幅度较小.同时应当指出,交通流稳定与不稳定的理论临界速度与油耗降低显著与不显著的临界速度之间并不能发现固定的定量关系.
4 结 论
研究自动驾驶交通流相比于手动驾驶交通流的油耗影响,在周期性扰动的交通震荡下,不同车队初始速度等条件时的平均油耗率的降低范围约为0.004 4%~60.389 4%.同时从交通流稳定性的角度考察了平均油耗率的降低与稳定性提升之间的内在关联性,自动驾驶交通流将手动驾驶交通流从不稳定状态转变为稳定状态时,平均油耗率易得到显著降低,而手动驾驶交通流稳定的速度范围,平均油耗率的降低较小.表明稳定性的提升与油耗降低幅度之间存在定性的影响关系,该结论可为大规模自动驾驶车辆背景下的交通油耗控制从交通流平稳性的角度提供理论参考.
研究结果是基于数值仿真与理论分析相结合的方式得到的,自动驾驶车辆的真车实验尚不普及,相关实地测试处于逐步试点阶段,下一步的研究将针对性地采集小规模自动驾驶车辆实地测试的微观数据,进一步充实和完善现有研究结论.
