基于IC卡数据的公交通勤熵变模型的构建与应用

李 军，郑培庆

(中山大学智能工程学院广东智能交通系统重点实验室，广州510006)

0 引 言

通勤是城市居民出行活动的重要组成部分，基于通勤测度城市职住空间关系有利于对城市居民的通勤行为有进一步的认识，从而有针对性地进行资源优化配置.在不改变城市形态的情况下，以一个具体的指标来衡量减少平均通勤距离的相对困难程度，对城市规划具有极其重要的作用.多数学者以基于线性规划的最小平均距离作为社会通勤最优值[1-3]，但是不可能强迫个人产生集体社会最优结果，最大熵双约束出行分布模型提供了一种理想的分析工具.为探讨城市空间结构内部相互作用水平和降低平均通勤距离的可能性，O'Kelly 基于最大熵双约束出行分布模型提出了effort 指标[4]，这一指标的提出丰富了过剩通勤理论框架.

但在实际应用中仍有一些问题需要解决，本文从两方面进行探讨.一是单元问题对熵变模型的影响.单元问题是过剩通勤理论发展中一个重要的影响因素，有学者称之为可塑性面积单元问题(MAUP)[5-8].多位学者探讨了单元问题对过剩通勤指标的影响[9-10]，结果表明，单元问题对过剩通勤指标的影响是有限的.Niedzielski等也利用地理信息系统与泰森多边形分形方法探讨了过剩通勤理论相关指标和单元问题之间的关系[11].但是相关研究主要是基于人口普查数据对熵变指标的有效性进行评价[3-4]，单元问题对熵变指标的影响仍有待探讨.二是数据的使用对模型构建和应用的影响.关于过剩通勤的研究主要是基于人口普查数据和问卷调查数据，在当前大数据背景下的研究较少，刷卡数据更多地应用在上下站点的推算、出行特征挖掘等方面，如何基于公交刷卡数据构建和应用通勤熵变模型有待研究[12-20].

本文主要基于广州市IC 卡数据，探讨公交通勤熵变模型的构建和应用，以及单元问题对模型的影响，为通勤熵变模型在城市公共交通出行中的应用奠定坚实的基础.本文的贡献主要有以下几点：一是理论完善，分析通勤熵变模型的单元问题，为模型应用提供了单元划分的依据；二是数据使用，探讨基于IC 卡数据公交通勤熵变模型的构建和应用的全过程；三是模型应用，以广州市为例探讨了模型在公共交通通勤评价中的有效性和可行性.

1 问题描述与建模

本文研究框架如图1所示.首先基于Wilson最大熵、双约束重力模型和公交出行特点构建公交通勤熵变模型，然后以广州市IC卡数据为例，探讨从数据准备到模型求解的完整应用过程，其中基于泰森多边形方法重点分析单元问题对模型的影响，使用泰森多边形主要是为了从单元大小和单元划分方式两个方面对单元问题进行探讨.

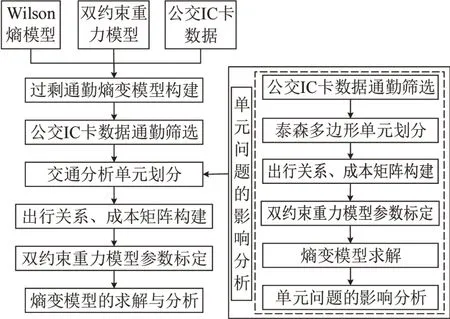
图1 研究框架Fig.1 Research framework

1.1 公交通勤最大熵模型

基于Wilson 最大熵模型和O'Kelly 的熵变指标[4,21-23]，构建公交通勤最大熵模型为

式中：Z为变量；qij表示小区i到小区j之间的出行量；Oi为小区i的出行发生量；Dj为小区j的出行吸引量；cij为小区i和小区j之间的距离成本；Q为总的交通生成量，可通过求得；为平均通勤距离，为公交通勤总距离.由于公交通勤中距离是一个主要的因素，且变化较小，比较稳定，所以使用欧氏距离作为单元之间的成本.

利用拉格朗日乘子法对式(1)～式(4)求解，即

式中：λi、μj和β分别为拉格朗日乘子；L为右边等式的赋值，无特殊含义.

进行一阶求导，令导数为0，可得qij值为

将式(6)代入式(1)，可求得省去常数项的最大熵H为

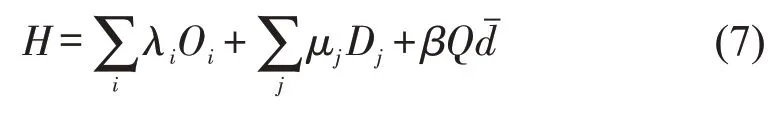
式中：H表示平均通勤距离为时的最大熵.

为求得式(7)中λi、μj和β的值，采用指数型双约束重力模型对公交通勤进行探讨，模型为

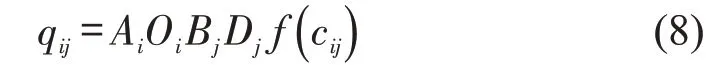
式中：Ai和Bj为平衡系数；f(cij)为指数型函数.

对比式(8)，式(6)具有双约束重力模型特征，使用双约束重力模型为最大熵生成关键参数，即

结合式(7)，式(9)～式(11)，以及公交出行的特点，可以基于双约束重力模型构建公交通勤最大熵模型.

1.2 通勤熵变模型

通勤熵变模型Ec为初始和优化两种状态下的最大熵的差值，表示从初始状态达到优化状态需要付出的努力，从而衡量公交通勤优化的可能性.

式中：和分别对应初始状态(用0 表示)和优化状态(用1表示)下的最大熵.

初始和优化状态对应的最大熵值为

因此Ec可看成由起始、终止和通勤距离3 部分构成.

2 案例分析

选取广州市居民公共交通出行作为研究对象，包括常规公交和地铁两种出行方式，研究区域的地理空间范围为：113°10′11.60″E～113°32′0.93″E，23°2′25.89″N～23°15′36.86″N，包含广州市中心城区(越秀区、荔湾区、海珠区、天河区、黄埔区、白云区南侧、番禺区北侧)和佛山东侧部分地区，如图2所示.

2.1 通勤筛选

使用数据源为2014年1月6～12日(包含5个工作日，2 个周末)4 192 521 张广州市公交IC 卡数据(包括“羊城通”和“岭南通”).经过数据清洗与站点匹配后[24]，得到公共交通出行活动数据总量为：22 429 915条出行记录，覆盖中心城区2 905个公交/地铁站点(包括2 801 个公交站与104 个地铁车站).对具有完整OD信息的数据进行简单的推断和筛选获得通勤数据，过程如下.

图2 研究区域Fig.2 Study area

(1)交通出行时间分布统计，确定通勤时间范围.将1 d 从00：00：00 开始以30 min 为单位划分成48个区间，统计每个时间区间的交通出行量，其中换乘数据只考虑起讫点，不考虑中间换乘站点，如图3所示.

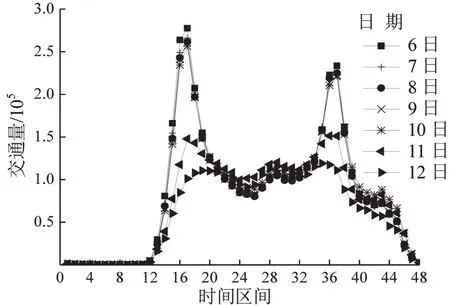
图3 各区间时间段内交通生成量Fig.3 Travel volume in different time periods

从图3可以看出，相较于星期六和星期日，工作日的早高峰大概在06：00：00-09：00：00，晚高峰大概在17：00：00-19：00：00.为获得更加完整的通勤者，对早晚高峰时间段进行扩展，如表1所示.

对比可以发现，对出行时间段进行扩展，能够获得更多的出行对，因此基于扩展的早晚通勤时间段进行通勤者筛选.

(2)通勤初步筛选.分别对早晚通勤时间段内的数据进行统计筛选，以每周最少3次具有相同的起讫点作为判定条件，得到具有通勤可能性的通勤者和通勤起讫点.

表1 不同时间段内具有相同起讫点的出行数量Table1 Number of trips with same origin in different time periods

(3)通勤匹配，确定通勤者和职住地点.对早晚通勤时间范围内的可能通勤者进行匹配，删除可能的非通勤者，删除条件主要有：只在早/晚通勤时间内出行，在早/晚通勤时间内多次往返出行.

经过上述步骤筛选得到218 520 个具有明显通勤特点的通勤者，其中包含1 840 个起始站点，1 739个终到站点.

2.2 单元问题

使用泰森多边形进行区域的划分，单元数量从25到500，每次增加25，每种单元格数量下进行100次的单元格划分和计算.将站点出行关系匹配成单元之间的出行关系，单元内部出行距离使用近似圆的半径(面积使用单元实际面积)，单元之间出行使用质心间的欧氏距离，利用双约束重力模型求解方法(误差设置为3%)进行参数标定，求得最大熵H( 0)和H(1).为了探讨单元问题对通勤熵变指标Ec的影响，计算并比较了不同平均通勤距离优化度的情形下Ec的变化趋势，如图4所示.当单元格数量为25 和50 时，由于Ec的波动范围太大，而且部分情况平均通勤优化之后H(1)趋于无穷大，最终得到单元数量与Ec在不同优化度下的关系图，如图4所示.

根据图4可以发现：①当城市平均通勤距离优化度较小时，Ec几乎不受单元问题的影响；当接近城市理想平均最小通勤距离时，Ec在单元数量较少时波动范围较大，但是随着单元数量的增多，Ec变化逐渐收敛，单元问题对Ec的影响有限.因此，在计算Ec时，应尽量保证较多的单元格数.②Ec≥0 且随优化度的增加而不断增加，当优化度逐渐接近城市理想平均最小通勤距离时，Ec趋于无穷大.这也表明，优化城市平均通勤距离所需付出的工作量随优化度的增加而不断增加，当达到一定值时，即使付出再多的努力，也无法优化城市平均通勤距离.

基于上述影响分析，进一步探讨方格划分这一泰森多边形中的特例.对研究区域进行了1 km×1 km 的单元格划分，共得到950 个单元格，将城市居民公共交通出行站点与所得单元格进行匹配，删除出行站点为0 的单元格，最后得到545个具有出行起点属性的单元格和519 个具有出行终点属性的单元格.对比图4可以发现，基于约1 km×1 km 的网格划分时，Ec几乎不受单元划分方式的影响，这也符合公交站点服务半径的特点.因此，在基于公交刷卡数据对Ec进行计算时，采用约1 km×1 km 的单元格划分适合作为城市公交通勤熵变模型中网格划分的方式，为通勤熵变模型在城市公共交通规划中的应用提供基础.

图4 单元数量与Ec 在不同优化度下的关系图Fig.4 Relationships between number of zones and Ec under different optimization degrees

在对Ec单元问题的研究的基础上，对Ec各部分单元问题的影响也进行了探讨，结果如图5所示，主要包括单元数量与Ec的起始部分、终止部分和通勤距离部分在不同优化度下的关系图、单元数量与β在不同优化度下的关系图.

从图5可以发现：①Ec各部分受单元问题影响与Ec基本保持一致；②Ec起始部分的值远大于终止部分的值，表明在城市通勤距离优化过程中，更多的是需要努力对起始部分进行优化，终止部分进行小幅的调整；③Ec通勤距离部分值随着优化度的增加逐渐减小(绝对值是增大的)，这表明在城市通勤距离优化过程中，不需要过多的投入资源去改善居民出行的选择，通勤距离部分的熵值会随着起始部分和终止部分的优化而变化；④β值随着优化度增加而不断增大，说明双约束重力模型中β值受优化度和单元问题的影响.

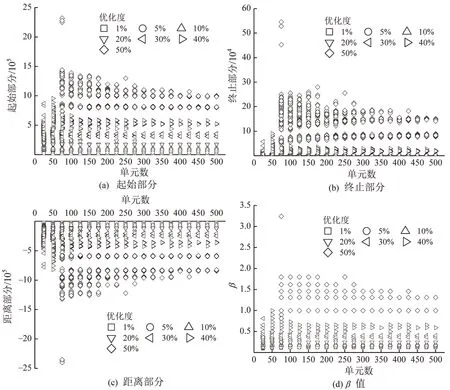
图5 单元数量与Ec 的各部分在不同优化度下的关系图Fig.5 Relationships between number of zones and various parts of Ec under different optimization degrees

2.3 模型应用

基于以上结论，以广州市居民公共交通出行的刷卡数据为例进行实例分析，探讨应用通勤熵变模型的可行性和有效性.基于1 km×1 km 的网格划分得到Oi、Dj和cij，利用双约束重力模型(误差设置为3%)求解方法，求得关键参数值Ai、Bj，基于通勤熵变模型得到熵变指标值(平均通勤距离优化度设置为3%)，结果如表2所示.

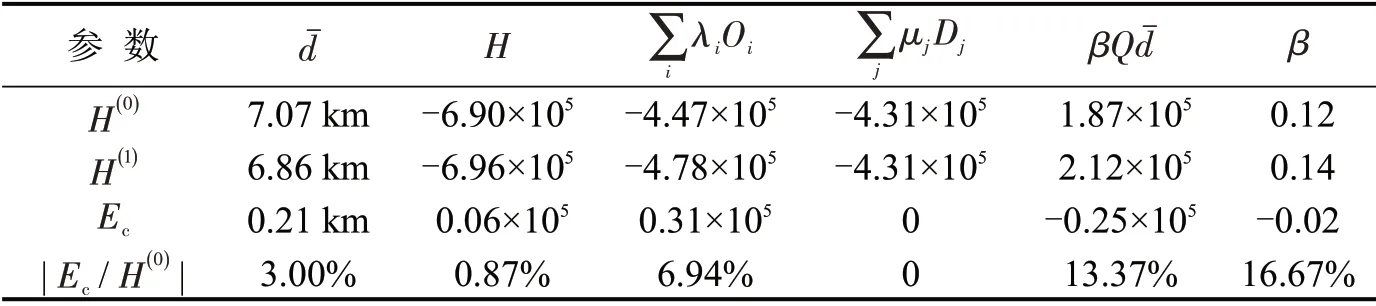
表2 平均通勤距离优化时计算结果Table2 Calculation results when average commute distance is optimized

从表2中可以看出，当广州市居民平均通勤距离减少3%时，相对困难程度Ec为0.06×105，占最大熵的0.87%.对于Ec各部分而言，可以发现，起点部分为0.31×105，终点部分的值为0，平均通勤距离部分为-0.25×105，即居民平均通勤距离减少3%时，只需对居民出行起点进行改善就可以实现优化目标.因此，在其他条件不变的情况下，熵变模型可以用于衡量减少平均通勤距离的难易程度，可以评价改变城市通勤活动的有效性.

3 结 论

本文主要以熵变模型作为研究对象，基于IC卡数据从通勤数据的筛选、单元问题和模型应用3个方面，分析基于IC 卡数据的公交通勤熵变模型的构建和应用过程，探讨城市公交通勤网络中通勤熵变模型中单元问题的影响，以广州市居民公共交通出行的IC卡数据为例分析模型在城市公交评价中的可行性和有效性.结果表明：城市公交通勤的平均通勤距离优化较小时，熵变模型几乎不受单元问题的影响；当优化度逐渐接近城市理想通勤距离时，指标在单元数量较少时波动范围较大，但是随着单元数量的增多，不受单元问题影响.采用大约1 km×1 km的网格划分适合作为城市公交通勤熵变模型中单元划分的方式，符合公交站点服务半径特点.在城市公交通勤网络中，基于IC卡数据能够构建公交通勤熵变模型、衡量平均通勤距离减少的难易程度和检验相关政策改变通勤行为的有效性.本文仅仅从单一IC 卡数据源对城市公交通勤进行评价，后续研究将融合卡口数据、停车场数据等多源数据对整个城市的通勤特征进行研究.