数学名题:为学生种下一颗数学研究的种子
2020-02-28蒋守成
○蒋守成
主题拓展教学基于对教材内容的系统把握与对学生学习经验、生活经验的准确理解两个层面,以主题为核心建设主题课程资源,为学生提供只有在数学学习中才会经历和体验并建立起来的独特的思维方式。
数学名题中蕴含了深厚的数学史,隐藏了丰富的数学思想方法,介绍了数学家发现问题和研究问题的历程,具有典型性和广泛的影响力。因此,我们以数学名题为主题,为学生种下一颗数学研究的种子,来激活凝固的书本知识,使知识恢复到鲜活的状态,实现书本知识与学生发现问题、解决问题、形成知识过程相关联,实现书本知识与学生的生活世界和经验世界相关联,丰富和拓展数学学科的育人资源,全面发展学生的思维。
一、解读教材,拓展数学名题的育人价值
数学名题是指在数学发展历史长河中形成,并对数学发展、数学应用和数学教学等方面起过或仍起着重要作用的数学问题。
例如:杨辉三角、哥尼斯堡七桥问题、哥德巴赫猜想、鸡兔同笼……这些著名的数学问题是数学家经过几百年甚至上千年的不断探索与思考的智慧结晶,在数学史上产生较大影响,对数学发展有一定的推动作用。不同版本的小学数学教材中也都编排了一些数学名题,让学生经历像数学家一样研究的过程,感受新概念的诞生,体悟新方法的形成,感悟深厚的数学文化,体会数学在人类发展史中的作用。
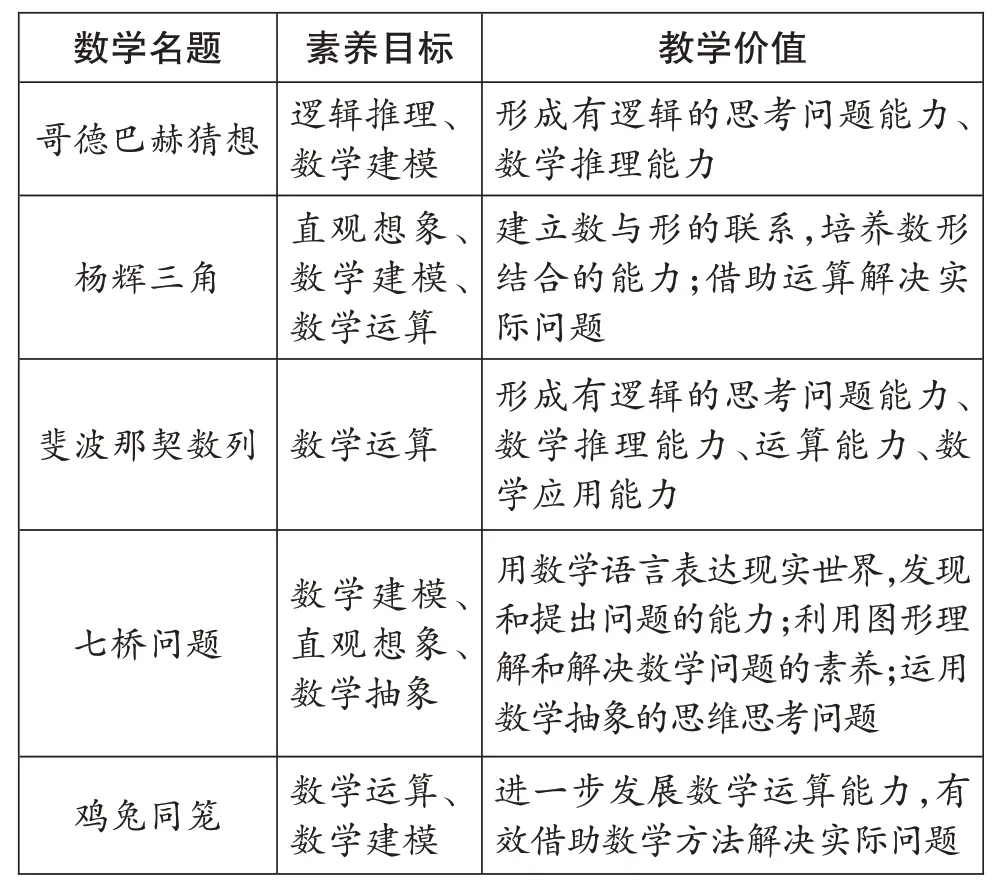
数学名题蕴含着重要的数学思想方法,是提升学生数学素养的有效载体。例如,“物不知其数”蕴含了同余的思想方法,“七桥问题”不仅是抽象的典型实例,同时也蕴含转化的思想方法。因此,我们应对数学名题的素养目标和教学价值进行定位,为课程资源开发和课堂教学提供帮助。(下表是部分数学名题的素养目标和教学价值定位。)
数学名题哥德巴赫猜想杨辉三角素养目标逻辑推理、数学建模直观想象、数学建模、数学运算斐波那契数列数学运算七桥问题鸡兔同笼数学建模、直观想象、数学抽象数学运算、数学建模教学价值形成有逻辑的思考问题能力、数学推理能力建立数与形的联系,培养数形结合的能力;借助运算解决实际问题形成有逻辑的思考问题能力、数学推理能力、运算能力、数学应用能力用数学语言表达现实世界,发现和提出问题的能力;利用图形理解和解决数学问题的素养;运用数学抽象的思维思考问题进一步发展数学运算能力,有效借助数学方法解决实际问题
其实能在小学数学课堂上渗透的数学名题还有很多,比如“省刻度尺”“和尚分馒头”“棋盘上的麦粒”“李白喝酒”“田忌赛马”“四色猜想”“冰雹猜想”“孪生素数猜想”……我们进行数学名题的主题教学研究,并不是要求学生做高深的数学研究,只是为学生创设一个可以像数学家那样“想”的空间,让学生经历和数学家一样的研究历程,感受真理探索的艰辛,帮助他们形成不唯书、不唯师、不唯上的批判性思维,形成独立思考、自由探索的数学品质,拓展数学学科的育人价值,全面提升学生的数学素养。
二、整合教学,放大数学名题的教学价值
学会思维是学生思维发展的必由路径,“学会”强调的是过程,而非结果,每个人都要学会思维,但学会的标准是多元的,学会的路径是灵活的。我们依据学生的年龄特点和认知水平,基于教材内容,精心选择开发了52 个小学生能懂的数学名题,为学会思维提供过程支架,从中年级的数学阅读和高年级的名题研究两个路径来放大数学名题的教学价值。
(一)数学名题主题阅读。
我们在中年级进行数学名题阅读欣赏,让学生感受名题中的数学思想和方法,吸取名题中的数学文化和数学精神,提升对数学学习的兴趣,感受数学的魅力。例如:我们将数学名题改编成数学童话,供三四年级学生进行阅读。
时空穿梭解名题系列之《和尚分馒头》
点点和芳芳都是数学爱好者,她们很想了解古代人是如何学习数学的。一次偶然的机会,她们得到了外星人留在地球上的时空穿梭机,真的实现了时空穿梭,眨眼间便回到了明代。
她们来到一座寺庙前,点点说:“我们进去玩玩吧!”可是当她们来到寺庙门口便被几个和尚拦住了:“寺庙只接待香客,不接待游客!”这时一位老伯说:“小朋友,如果你们能回答上我的问题,我就分几炷香给你们。”点点说:“行,什么问题?”老伯说:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”点点听得有些摸不着头脑,便问芳芳:“这是什么意思啊?”芳芳说:“这是明代《算法统宗》中的问题,意思是说一百个和尚吃一百个馒头,大和尚每人吃三个,小和尚每三人吃一个,大小和尚各有多少人?”
点点说:“原来是这么回事,这题我会解。把1个大和尚与3个小和尚看成一组,那每组得分4个馒头,100÷4=25(组),说明有25 个大和尚、75 个小和尚。”
老伯惊叹地问道:“小朋友好聪明,你叫什么名字?”点点也不客气地问道:“你叫什么名字啊?”老伯笑道:“我叫程大位。”芳芳吃惊地说:“点点,他就是明代大数学家程大位,《算法统宗》就是他写的!”点点一听愣住了,老伯笑道:“我们现在就去烧香吧!”
通过数学阅读把抽象、枯燥的数学问题加工成有趣且适合阅读思考的学习材料,对学生进行数学思想、数学文化的渗透,将数学内在的理性精神以一种可以触摸、可以表达、可以分享的方式告诉他们,让他们去感悟,去体验,去传承。
(二)数学名题研究。
我们在高年级进行数学名题系列研究,从著名的数学问题“哥德巴赫猜想”“四色猜想”“冰雹猜想”“孪生素数猜想”“省刻度尺”“雪花曲线”“杨辉三角”等出发,化复杂为简单,化深奥为浅显,让学生在学习过程中像数学家一样去工作、思考和交流,培养数学学习的品质,让学生的思维生长在研究过程中可见。
例如,我们以世界三大猜想之一的“四色猜想”为研究主题,让学生充分经历观察、实验、猜想、验证的过程,体悟推理和模型思想。研究过程分三个板块:
板块一:引导学生自己提出猜想。
1.解决问题,引发猜想。呈现江苏省地图提出问题:从地图上我们可以看出江苏省由13 个城市组成。如果要把江苏地图涂上颜色,并且相邻两个城市要涂不同的颜色来区分。想一想,可以用几种颜色?
学生回答有13种、12种、11种等等,答案不一致,但都能够区分。
小结:看来按这样的要求来涂色,方法可不止一种。那么到底最少需要几种颜色就足以保证相邻的两个城市颜色不同了呢?
2.动手操作,探寻结论。按要求给下面3 个图形涂上颜色,涂完后说明理由。
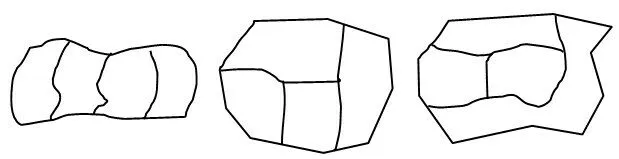
(1)每个图形中相邻的两块颜色不同。
(2)用的颜色要最少。
学生汇报后,教师追问:刚才我们研究的这3个图形都被分成了4块,为什么只有第3个图需要4种颜色,而前2个图不需要4种颜色呢?
同桌交流后分享:因为第三个图中的每一块都和其他三块相邻,而前2个图形中并没有这样。
3.继续探索,提出猜想。用你喜欢的方式把下面的图形任意分成5 块、6 块、7 块,按刚才的要求涂色,你能发现涂色的规律吗?
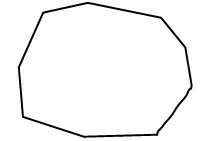
学生分享比较发现:把一个图形任意分成4块、5 块、6 块或7 块,只要用4 种颜色来涂色,就足以保证相邻的2 块颜色不同。也有学生大胆地提出:把一个平面图形分成若干块,只要用4 种颜色涂色,就足以保证相邻的两块颜色不同。这也就是著名的世界三大猜想之一:四色猜想。
板块二:介绍“四色猜想”的发现和提出的过程。
1852 年,一位名叫葛斯瑞的英国绘图员发现了一种有趣的现象:在每幅地图上只要用4 种颜色来着色,就足以把有公共边界的国家(或地区)分开,即把相邻的国家(或地区)涂上不同的颜色。如果用数学语言来表示四色猜想就是:将一个平面图形任意分为大于或等于4 个的不重叠区域,只要用1、2、3、4 四个数字来标记每个区域,就可以保证相邻的两个区域不会出现相同的数字。由此可以告诉学生:数学猜想不一定要数学家提出来,我们每个人都可以提出数学猜想,然后进行验证猜想是否正确,这是一种很好的数学思考方法。
板块三:自己验证四色猜想,感受猜想的奇妙。
提问:让你来证明四色猜想,你会怎么做?(举例)
验证:学生借助研究单上的地图(江苏地图、北京地图、宁夏地图),用数字表示颜色的方法来验证,发现都是4种。
追问:我们用了3 幅地图验证了四色猜想,你觉得这样的证明够不够?这样的例子还有很多,那科学家们又是怎样来证明四色猜想呢?我们一起来了解一下。介绍数学家证明四色猜想的历程,指出1976年9月,美国数学家阿佩尔和哈肯教授,用计算机做了100 亿次的判断后,最终完成了四色猜想的证明。
其实很多猜想就像“四色猜想”一样来自我们的日常生活,例如“冰雹猜想”就是来自70 年代美国大学里风靡的数学游戏。当我们经常用数学的眼光去观察日常的学习和生活时,也许下一个提出著名数学猜想的人就会是你!
数学名题的研究不仅使数学教学变得有意思,也让数学教学变得更有意义,让学生不仅仅停留在“知道”层面,更能够促进学生把问题想得更清晰、更全面、更深刻、更合理,能够体会人类认识世界、数学化地刻画世界的过程,体悟到数学自身的魅力。
