基于深度学习的氟化铝添加量和出铝量预测

2020-02-25常家玮曾水平

世界有色金属 2020年22期

常家玮，曾水平

（北方工业大学电气与控制工程学院，北京 100144）

铝电解作为一个复杂的工业生产过程，维持电解过程的两大平衡（能量和物料平衡）是保障其生产高效稳定运行的关键因素，然而铝电解的两大平衡受多种因素、指标的共同影响，耦合关系复杂，对氟化铝添加量和出铝量的正确决策是维持两大平衡，保证经济效益最直接、有效的途径。添加氟化铝，可以降低分子比，降低电解温度，提高电流效率；氟化铝添加过多，则会造成氧化铝溶解降低，未溶解的氧化铝堆积在槽底容易产生病槽。出铝量偏少，铝水平偏高，电解槽热损增加，电解温度偏低，会造成冷槽甚至病槽；出铝量过多，电解温度升高，电流效率降低，又容易引发阳极效应。因此，获取合适的氟化铝添加量和出铝量决策值，对于稳定生产和提升效益至关重要。

在目前的实际工业生产中氟化铝的添加量主要是通过计算机专家系统进行决策，但由于铝电解过程是个时变、非线性、强耦合的大时滞复杂系统，专家系统无法根据槽况的变化情况，较好地对其进行决策[1]；出铝量的决策主要是根据“铝水有效值法”进行计算和管理，其测量和计算过程比较繁琐，操作精度要求高，在非正常槽况下仍然需要车间管理人员依据经验进行设置[2]。近年来，各专家学者也提出了一些氟化铝添加量或出铝量的控制策略，如：文献[1]根据生产数据求解回归相关系数，研究了一种氟化铝添加量决策模型；文献[3]提出了基于回归分析、遗传算法、支持向量机的氟化铝添加量控制策略；文献[4]提出了一种在线采集和离线测量相结合的氟化铝添加方法；文献[5]通过模糊控制实现对氟化铝添加量和出铝量的控制。关于神经网络的运用方面，刘冰[6]和魏玉倩[7]分别使用了RBF 和BP 神经网络进行了预测研究，取得了较好的效果。

本文充分考虑铝电解过程非线性、大时滞、强耦合的特点，利用历史生产数据，将特征选择得到的强特征数据作为LSTM 神经网络的输入，氟化铝添加量和出铝量作为输出对网络进行训练，通过训练、测试和验证，能够满足工业生产要求。

1 特征处理

特征处理作为特征工程的核心内容，包括了数据清洗、规一化处理、特征选择等内容。对于铝电解工业，影响其生产过程的参数众多，同时各参数之间又相互耦合，如电解温度、氧化铝浓度、氟化铝添加量、出铝量、工作电压等多达二十几项指标，其中一个指标的调整会引起其他参数均产生相应的变化。因此为了避免出现过拟合，使得试验结果准确可靠，数据清洗和特征选择必不可少。

1.1 数据分析与清洗

本文数据来源于国内某铝厂402 号槽的实际生产日报，包括电流、电压、下料量、铝水平、出铝量、氟化盐下料量（即氟化铝添加量）等总计20 维2477 组数据，经过对该批数据的检索和统计，存在数据缺失和异常的情况，因此为了降低坏数据的不良影响，首先对其进行数据清洗。

删除缺失值较多的三个特征“炉底压降”、“炉帮”、“伸腿”。同时，本文主要研究的是正常生产阶段对氟化铝添加量和出铝量的预测，因此选取了启停槽中间正常生产阶段的数据，对于存在的缺失值使用KNN 算法进行填补，最后使用箱型图筛选出异常值，并将低于下限和高于上限的异常值分别使用下限值和上限值进行替代，最终得到所需要的数据集。

1.2 数据规一化处理

本数据集具有多达17 个参数指标，同时各个指标的数量级差异较大，如氟化铝添加量平均值为26.38，但出铝量平均值达2184.28，因此必须进行数据归一化处理。本文采用离差标准化算法，该算法将数据映射到[0,1]之间。

式中：xmin——原数据所在列最小值；xmax——原数据所在列最大值。

1.3 随机森林做特征选择

随机森林属于Embedding（嵌入法）特征选择算法的一种，是基于集成思想对决策树算法的进一步优化改进，它通过Bootstraping（自助）采样法和Bagging（装袋）算法生成一片由m 个不同的决策树组成的“森林”，其随机的特点体现于：①随机地为每颗决策树选取数据样本（随机有放回地从K 个原始数据样本中重复抽取k 个数据样本，k＜＜K）；②随机地为每颗决策树分配不同的特征（随机地从原始数据样本的N 个特征中选取n 个特征，n＜＜N）。正是这两个特点使随机森林算法显著有效地降低坏数据对算法结果的影响，避免出现过拟合等问题。它既能解决回归问题，又能进行分类预测，同时可以对各个特征的重要性进行评价，方便了处理特征选择方面的问题，目前该算法已经在特征工程和分类预测领域得到了广泛使用[8，9]。

1.4 特征选择算法设计及结果分析

本文使用随机森林回归函数，算法输入为17 个特征当日的数据，输出为氟化铝添加量和出铝量第二天数据，共计2345 组，训练集和测试集分别占80%和20%，建立由150个树组成的森林对随机森林进行训练和预测。

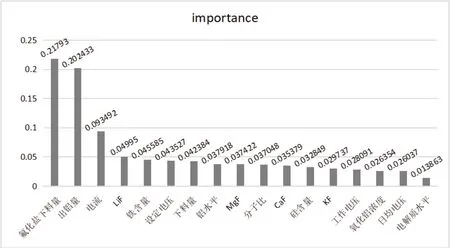
图1 特征重要性排序

得到特征重要性排序如图3 所示，从图中可以看出当天的氟化铝下料量和出铝量对次日的影响最大，与实际相符从而验证了特征选择结果的正确性，经多次试验最终选取排名前10 的特征作为选取结果。

2 LSTM神经网络预测

2.1 LSTM 神经网络算法介绍

LSTM 神经网络是德国计算机科学家Jürgen Schmidhuber 和Sepp Hochreiter 于1997 年提出的一种为解决深度学习容易出现梯度消失和梯度爆炸问题的优化版RNN（循环神经网络）[10]。其遗忘门决定了删除先前时刻的信息，输入门决定了保存当前时刻的信息，输出门决定了输出到下一时刻的信息，正是这三种门结构对信息的筛选，解决了梯度消失和梯度爆炸问题，同时保证了对重要信息的长期记忆。

2.2 LSTM 神经网络建模

本文用于神经网络训练和测试的数据共计2335 组，其中训练集占80%，测试集占20%，10 组数据作为验证数据，使用Python 经训练和测试数据多次试验后，搭建如下LSTM 神经网络结构：

输入层：氟化铝下料量、出铝量、电流、LiF、铁含量、设定电压、下料量、铝水平、MgF、分子比10 个特征当天的数据

隐含层：2 层，每层50 个LSTM 神经元

输出层：氟化铝添加量、出铝量2 个特征次日的数据

表1 其他参数设置

2.3 LSTM 神经网络训练、预测及验证步骤

第一步，对输入和输出数据使用离差标准化算法进行归一化处理；

第二步，对数据集进行划分，将80%数据作为训练集，20%作为测试集，最后再选取10 天的数据对网络预测效果再次进行验证；

第三步，使用搭建好的神经网络对训练集的输入、输出数据进行训练；

第四步，使用训练好的模型对测试集的输入数据进行预测；

第五步，将输出的预测值与真实值进行反归一化处理并计算MAE（平均绝对误差），同时画出预测值与真实值的曲线对比图；式中：n——测试集数据行数；

yi——第i 行真实值；

yˆi——第i 行预测值。

第六步，选取训练集和测试集以外连续10 天数据对网络进行验证。

3 训练和预测结果分析

训练集数据在迭代48 次之后测试集的损失函数稳定在0.0122～0.127 之间。

图2 损失函数衰减图

使用测试集数据进行预测，得到预测值与真实值的曲线拟合效果较好，其中氟化铝添加量的MAE1=2.341，出铝量的MAE2=32.566，均在铝电解工业误差允许范围内，曲线拟合情况如图3、图4 所示。

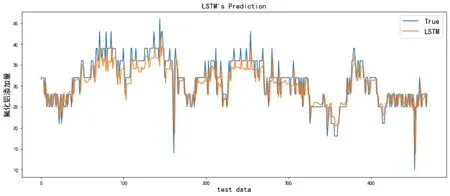
图3 氟化铝添加量预测值与真实值曲线拟合

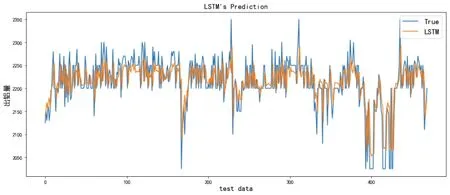
图4 出铝量预测值与真实值曲线拟合

最后选取连续10 天数据进行验证得到预测结果如表2、表3 所示。

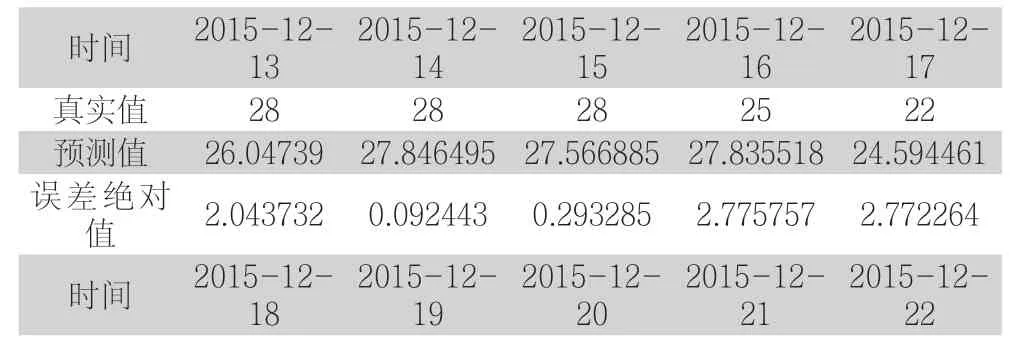
表2 氟化铝添加量预测验证

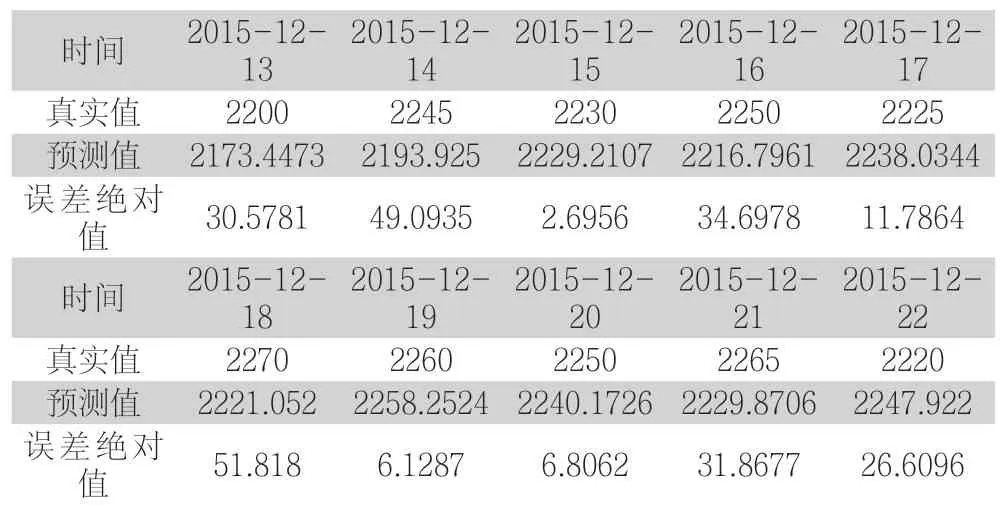
表3 出铝量预测验证

从验证结果可以得出：氟化铝添加量预测值与真实值相比平均绝对误差为1.32，最大误差2.78，最小误差0.09，该误差不影响实际生产中参数的稳定[7]；出铝量预测值与真实值相比平均绝对误差为25.21，最大误差51.82，最小误差6.13，同时相邻两天出铝量的相差未超过50kg，使得生产稳定性得以保障[2]，因此本算法预测的氟化铝添加量和出铝量符合实际生产要求。