沥青混合料铺筑温度场的有限差分仿真模型

王黎明， 李 崟

(东北林业大学土木工程学院,哈尔滨 150040)

热态沥青混合料的温度严重影响着压实效果,碾压质量差会引致路面的早期损坏。这就需要道路工作者清楚在特定条件下混合料的降温规律,以便合理安排施工。而热沥青混合料冷却过程复杂,实地观测不能得出铺筑热扩散的全面规律,而建立仿真模型是解决问题的关键。

20世纪60年代,Corlew等[1]基于有限差分的显示格式建立了路面铺筑温度场的模型,但未考虑铺筑过程的层厚和材料热物性参数的变化,这使得该模型和服役期路面温度场无本质区别；1998年,美国明尼苏达州编制了可预估沥青混合料铺筑降温规律的“pavecool”程序[2]；但其未考虑对流换热、路表面洒水换热和铺层比热容的变化。中国虽然起步较晚,但众学者对沥青路面温度场的研究颇为翔实。孙洁[3]基于通用CAE软件,对铺筑阶段降温规律进行了系统研究,但其研究缺少铺层材料热物性以及天空阴晴状态对降温规律影响的考量；吕得保[4]基于实测得出了沥青混合料铺筑过程的温度回归模型,但由于观测因素的有限性,该模型的可信性有待商榷；王黎明等[5-6]运用Ansys软件对热态沥青混合料铺筑温度场进行了系统研究,对材料热物性和边界条件在铺筑过程的变化进行了细致研究,可实现高可信度的仿真,但该研究尚基于大型通用CAE软件，因此难以推广。现欲运用数值解方法,将求解混合料在铺筑过程沿厚度方向的一维非稳态温度场这一连续函数转化为确定沿厚度方向任意位置处每隔一定时间间隔的温度值,进而可在文献[6]的边界条件基础上,基于MATLAB、C语言等高级数学工具以实现混合料一维铺筑温度场的仿真。

1 基于数值解法的仿真模型

1.1 有限差分法

1.2 建立控制方程及定解条件

铺筑温度场的控制方程为

(1)

式(1)中：a为热扩散系数,m2/s，a=λ/ρc，其中，ρ、λ、c分别为材料的密度、导热系数和比热容,单位分别为kg/m3、W/(m2·℃)、J/(kg·℃)；∂t/∂τ为非稳态项；∂2t/∂x2为扩散项；t为材料的温度，℃；τ为时间，s；x为路面厚度，m。

定解条件包括初始条件和边界条件。由于压路机紧跟摊铺机,铺层沿厚度方向的各节点(除去与下承层的接触面)的初始条件为摊铺温度,接触面处的初始条件为下承层表面温度；下承层沿厚度方向的各节点的初始条件按照式(23)和式(24)计算。边界条件将在1.4节中做具体阐述。

图1 路面结构示意图Fig.1 Schematic diagram of pavement structure

1.3 建立内节点离散方程

由于隐式差分格式均无条件稳定,步长Δx和Δτ的取值不受限制,因此下述离散方程均采用隐式差分格式。

采用泰勒级数展开法,当非稳态项取向后差分(从p+1时刻的角度观察),扩散项取p+1时刻的中心差分,即

(2)

(3)

将式(2)和式(3)代入式(1)可得铺层内节点离散方程:

(4)

下承层内节点离散方程同理:

(5)

1.4 建立边界节点离散方程

建立边界节点离散方程采用热平衡法。

由能量守恒定律得铺层上边界节点离散方程:

(6)

铺层下边界元体N是由铺层材料和下承层材料共同组成的宽度为(Δx+ΔX)/2的元体,要将该元体的热物性参数重新求解并代入到铺层下边界节点离散方程中:

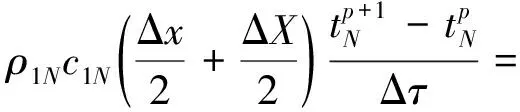
(7)

下承层上边界节点离散方程同式(7)。

由能量守恒定律得下承层下边界节点离散方程:

(8)

1.5 建立下承层两不同种材料接触节点离散方程

下承层中两不同种材料接触节点离散方程与内节点离散方程同理,只是将其换成对应的热物性参数、空间节点及步长,以第一和第二层下承层材料接触节点为例建立离散方程:

(9)

式(9)中：ρ23为第一和第二层下承层材料接触节点的密度,单位同前，ρ23=(ρ2+ρ3)/2；C23为第一和第二层下承层材料接触节点的比热容,单位同前，c23=(ρ2c2+ρ3c3)/(ρ2+ρ3)；λ23为第一和第二层下承层材料接触节点的导热系数,单位同前，λ23=2λ2λ3/(λ2+λ3)。

1.6 数学仿真模型的实现方法

由于采用有限差分法求解一维非稳态问题的代数方程组计算量较大,考虑到实际操作性,运用MATLAB数学软件,建立M函数文件并合理调用,将代数方程组编写代码,进而解出各空间节点在各时间节点下的温度值。

宏观上讲,此处涉及的代数方程组的系数矩阵M为三对角矩阵,由于M的特殊性,在编写代码时采用LU分解法求解。设未知数矩阵(温度矩阵)为T,常数项矩阵为Q,显然代数方程组数学表达式为MT=Q。令系数矩阵M由矩阵L和U的乘积表示,即M=LU,可推得LUT=Q,令UT=Y,则求解代数方程组MT=Q可转化为求解LY=Q,如此,大大节省了内存和计算时间。

2 仿真模型的各参数取值

2.1 基本假定

沥青混合料压实过程中铺层上边界暴露在空气中,主要涉及对流传热和辐射传热；铺层下边界只涉及热传导。 现建立如下假设:铺筑温度场为一维非稳态温度场；道路用材料均为均质的各向同性材料； 无内热源； 层间无热阻； 路面两旁路缘石以及研究深度范围的最底部绝热。 取铺层表面至下承层的42 cm深度处为研究深度范围。

2.2 热传导影响因素的参数取值

2.2.1 铺层厚度变化规律

由文献[5]的观测可知,沥青混合料的铺层厚度在三遍碾压后将不再明显压缩。层厚随压实次数的变化按文献[5]的计算方法推算。

Li=(1+tiRL)L

(10)

式(10)中：Li为压实i次后的层厚,i取0～3的整数,mm；L为设计厚度,mm；ti为压实i次后层厚变化系数,t0～t3分别取1、0.35、0.15、0；RL为沥青层松铺率,取0.25。

2.2.2 铺层材料密度变化规律

由文献[5]可知,推算模型如式(11)所示：

(11)

式(11)中：ρi为不同压实次数后的密度,kg/m3；ρcom为混合料最终压实密度,ρcom=Kρd。其中，ρd为试验室成型密度；K为标准压实度,%。

2.2.3 铺层材料导热系数变化规律

文献[2]的热物性测试结果表明,在25～75 ℃内,压实中的密级配沥青混合料(dense-graded asphalt mixtures, AC)的导热系数介于2.3～2.5 W/(m2·℃),而沥青玛蹄脂碎石混合料(stone matrix asphalt, SMA)的导热系数介于1.4～1.6 W/(m2·℃)。上述所有试样对温度均表现出相似的导热性能:温度从25 ℃上升到75 ℃,导热系数约减少0.2 W/(m2·℃)。将上述测定值进行回归,得到细粒和中粒式AC的导热系数随温度变化的规律为

λ=-0.004T+2.6

(12)

式(12)中：λ为沥青混合料导热系数,W/(m2·℃)；T为沥青混合料温度, ℃ 。

SMA的导热系数随温度变化的规律为

λ=-0.004T+1.7

(13)

文献[8]采用热线法进行了不同温度下导热系数的测定,得到了不同温度下的混合料导热系数,将其粗粒式AC的测定值进行回归,得粗粒式AC的导热系数一般性方程为

λ=-0.018T+3.406

(14)

2.2.4 铺层材料比热容变化规律

将文献[9]混合料的不同集料的比热容与温度进行线性回归,再用文献[5]的方法建立混合料的不同集料的比热容与温度的关系式:

c=KT+1 000

(15)

式(15)中：K为集料比热容温变系数,花岗岩1.581,玄武岩2.262,石灰岩3.006；T为沥青混合料温度, ℃；c为沥青混合料的比热容,J/(kg·℃)。

2.2.5 下承层材料热物性参数取值

在压实过程中,取下承层材料热物性参数为定值,如表1所示。

2.3 对流传热影响因素的参数取值

流体流过时与沥青铺层间的热量传递过程,称为对流传热,而影响对流传热量大小的参数是表面传热系数,现采用Solaimanian等[10]建立的经验公式来计算表面传热系数h。

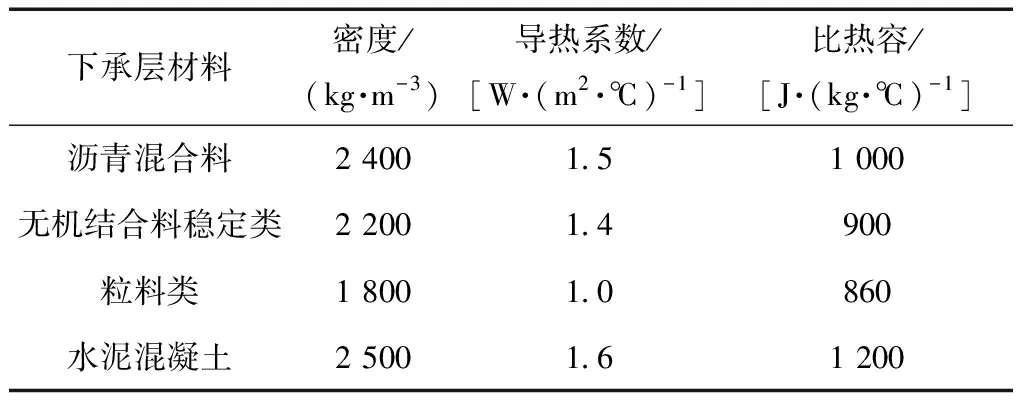
表1 不同下承层材料的热物性参数Table 1 Thermophysical parameters of different underlying materials

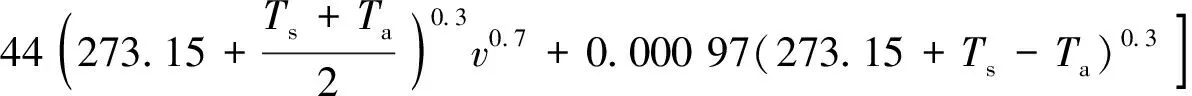
(16)

式(16)中：v为风速,m/s；Ts为路面表面温度, ℃；Ta为气温, ℃；h为表面传热系数,W/(m2·℃)。

2.4 辐射传热影响因素的参数取值

2.4.1 太阳辐射条件

采用文献[11]中的计算式来预估路面在晴天时的太阳辐射:

(17)

式(17)中：qDN为太阳直接辐射强度,W/m2；qdH为大气散射和逆辐射强度,W/m2；A为表观太阳辐射强度,W/m2；B、C分别为大气的消光系数和散射因子,无量纲；HA为太阳高度角，按式(18)计算:

sinHA=sinφsinδ+cosφcosδcosω

(18)

式(18)中，φ为纬度, 0～90°；δ为太阳赤纬,rad。

(19)

式(19)中：n为日数,1月1日起算；ω为太阳时角,(°)，计算公式为

ω=15(ST-12)

(20)

式(20)中：ST为真太阳时,以24时计，ST=北京时间+时差，时差=(当地经度-120°)/15°。

用太阳辐射透过率[5]对晴天太阳辐射进行修正,以得到实际天空状态下的太阳辐射:

k=100-8.121 9n

(21)

式(21)中：k为太阳辐射透过率,%；n为云量,云量不到天空的0.5/10时总云量为0,占全天1/10时总云量为1,其余依此类推。

取太阳辐射的吸收率α=0.95[5]。

2.4.2 有效辐射条件

晴天有效辐射强度qreff,sunny的计算[5]如式(22)所示:

(22)

式(22)中：ε为路面发射率；σ为斯忒藩-玻耳兹曼常量,其值为5.67×10-8W/(m2·K4)；tw为路面表面温度,K；tsky为有效天空温度,K,计算公式[12]为

(23)

式(23)中：tsurf为地面温度,取下承层20 cm处的温度,K,按式(24)推算[13]。

(24)

式(24)中：td为距下承层表面某深度d处的温度, ℃；tS0为下承层表面温度, ℃；d为距下承层表面的深度,m；τ为以小数计的时间参数。

采用式(24)推算下承层表面至20 cm深度处的温度场,而20 cm深度以下的温度场取定值,其值为20 cm 处的温度[5]。

下承层表面温度tS0可由实时气温Ta计算[13]:

tS0=1.1Ta+1.5+0.17e0.126Ta

(25)

由式(22)～式(25)计算晴天时的有效辐射,再根据实际的云量和云状对进行修正[14]:

qreff=(1-CN)qreff,sunny

(26)

式(26)中：qreff为实际有效辐射,W/m2；qreff,sunny为晴天有效辐射,W/m2；N为以小数计的总云量,0～1.0；C为系数,C=(Chnh+Cmnm+Clnl)/n,其中nh、nm和nl分别为高、中和低云的云量,Ch=0.15～0.2,Cm=0.5～0.6,Cl=0.7～0.8,为不同云状系数。

对于有效辐射发射率,取定值ε=0.93[5]。

2.5 压实过程

设共压实8遍,其中初压、复压和终压分别为2遍、4遍和2遍。取压路机3～4.2 km/h碾压,压路机紧跟摊铺机,初压同一点压实间隔为150 s；复压和终压同一点压实间隔为240 s,共计压实时间为1 740 s。

2.6 表面洒水散热的参数取值

取压路机洒水量200～400 kg/h,碾压速度约3 km/h,碾轮宽2 m,则单位面积单次碾压洒水量为33～67 g/m2,变成水蒸汽需热量82.5～167.5 kJ,设这些热量在碾压后60 s内耗散,得洒水散热热流密度为1 375～2 792 W/m2,由2.5节,在仿真试验中施加的路表面洒水散热热流密度在1 375～2 792 W/m2范围内取定值，施加洒水散热热流密度的时刻为第0、第3、第6、第10、第14、第18、第22和第26时间节点。

3 仿真模型检验

对仿真模型按照不同施工条件下铺筑过程的温度实测值进行验证,施工条件如表2所示,并将验证结果绘制于图2。

表2 用于仿真模型检验的不同施工条件Table 2 Simulation model verification different construction conditions

图2 不同施工条件下的仿真模型检验结果Fig.2 Test results of simulation models underdifferent construction conditions

由图2(a)和图2(b)可知,模型的仿真值与实测值在走势和数值上基本吻合；层中的仿真值与实测值有很高的一致性；层表的仿真值相对实测值有一定出入,但总体趋势和最终值有较好的准确性。图2(c)为包含下承层结构的全厚度仿真模型检验,各位置处的仿真值基本接近于实测值。

4 结论

(1)采用静态定值气温、风速、太阳辐射、表面洒水量、下承层初始温度场以及下承层材料热物性参数,动态变化值表面传热系数、有效辐射、铺层材料的密度、导热系数和比热容,在MATLAB软件中建立M函数文件并合理调用,得出了在特定条件下一维非稳态铺筑温度场的数值解。

(2)基于传热学理论和模型参数,确定了热态沥青混合料铺筑温度场的有限差分仿真模型涉及的参数取值。

(3)仿真模型可根据施工条件预估铺筑温度场的降温规律。不同条件下仿真检验证明,该模型具有较好的准确性和可信性,可作为仿真试验和实际应用的基础。