基于差分进化极限学习机的电力系统暂态稳定评估方法

李向伟, 刘思言, 高昆仑*

(1. 华北电力大学电气与电子工程学院,北京 102206； 2. 全球能源互联网研究院,北京 102209)

现代电力系统不断扩大的系统规模给调度运行带来了严峻的考验,不断复杂的网络结构,越来越多样化的负荷更使得系统的安全稳定运行显得更加重要[1]。

随着广域量测系统的快速发展,为电力系统提供了较好的实时数据支撑,而机器学习方法的不断推陈出新,也使得其在解决分类/回归问题上的准确性越来越高,因此数据和模型的不断进步,给暂态稳定评估提供了新的技术解决方案[2-8]。广域测量系统可以很方便地传输从发生故障到清除故障期间的相关功角、功率及电压等特征,而机器学习方法不需要建立复杂的数学模型,而是通过一定算法,建立输入与分类/回归任务之间的数学映射,对于训练完成的模型可以迅速对数据进行处理,因此,许多学者将其应用到TSA(transient stability assessment)上来。近年来,极限学习机(extreme learning machine, ELM)由于其不需要人为过多地去设置相关参数同时能够较为迅速地完成训练而成为当前解决分类/回归问题的热点模型。ELM不需要迭代,训练速度快,所需参数少,但也因此导致网络结果不稳定。如文献[2]提出了利用遗传算法和ELM对电力系统暂态稳定评估进行特征选择,大大减少了分类器的输入特征,但是也由于遗传算法和极限学习机均具有很强的随机性,因此使得模型的结果不稳定；文献[3]提出了利用改进粒子群算法优化极限学习机的权值和阈值,但由于改进粒子群算法搜索能力和精度不高并且容易陷入局部最优,因此限制了模型的分类准确率；文献[4]利用boosting框架集成了在线序贯极限学习机(OS-ELM),利用多个弱分类器集成强分类器,取得了较好的分类效果,但由于boosting框架对异常数据较为敏感,因此使得极限学习机的性能受到限制。文献[5]提出了利用遗传算法优化ELM的方法,但遗传算法收敛速度慢,需要凭经验选取过多参数,因此对分类效果产生较大影响。

为了提高ELM分类器的稳定性,提出一种基于差分进化算法[9](differential evolution,DE)优化极限学习机(DE-ELM)的电力系统暂态稳定评估方法。差分进化算法,相较于其他优化算法能够快速收敛,且不易陷入局部最优,因而引起了人们的广泛关注[10]。因此,将差分进化算法引入极限学习机并优化其权值阈值,避免了因随机选取而导致的分类器性能的不稳定；同时,为了剔除输入特征的冗余,进一步提升分类效果,引入了基于序列浮动后向特征选择(sequence floating backward feature selection,SFBS)的方法,进一步提升极限学习机的性能,并利用经典系统加以验证。结果表明,所提方法提升了模型鲁棒性,取得了很高的暂稳评估准确率,符合暂态稳定评估的应用要求。

1 差分进化算法优化极限学习机的模型

1.1 极限学习机

极限学习机(ELM)由三层神经元构成,如图1所示。设x=[x1,x2,…,xn]T、y=[y1,y2,…,ym]T(xi∈Rn、yi∈Rn)分别代表数据的输入和输出,中间层神经元数为l,激活函数选择g(x),则:

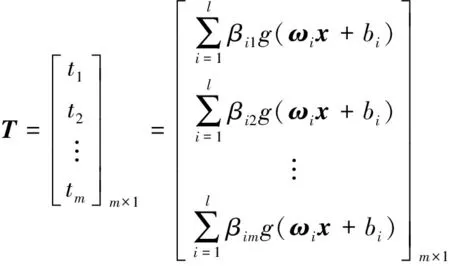
(1)

式(1)中,βi和ωi分别代表中间层的第i个神经元与输入层和输出层间的连接权重;βi=[βi1,βi2,…,βim],ωi=[ωi1,ωi2,…,ωin]；bi(i=1,2,…,l)为隐含层中第i个神经元的阈值。将式(1)用(2)式表示:

ΤT=H1×lβl×m

(2)

式(2)中,H=[g(ω1x+b1),g(ω2x+b1), …,g(ωlx+bl)],为隐含层输出矩阵。随后利用最小二乘得出权重β[11]。

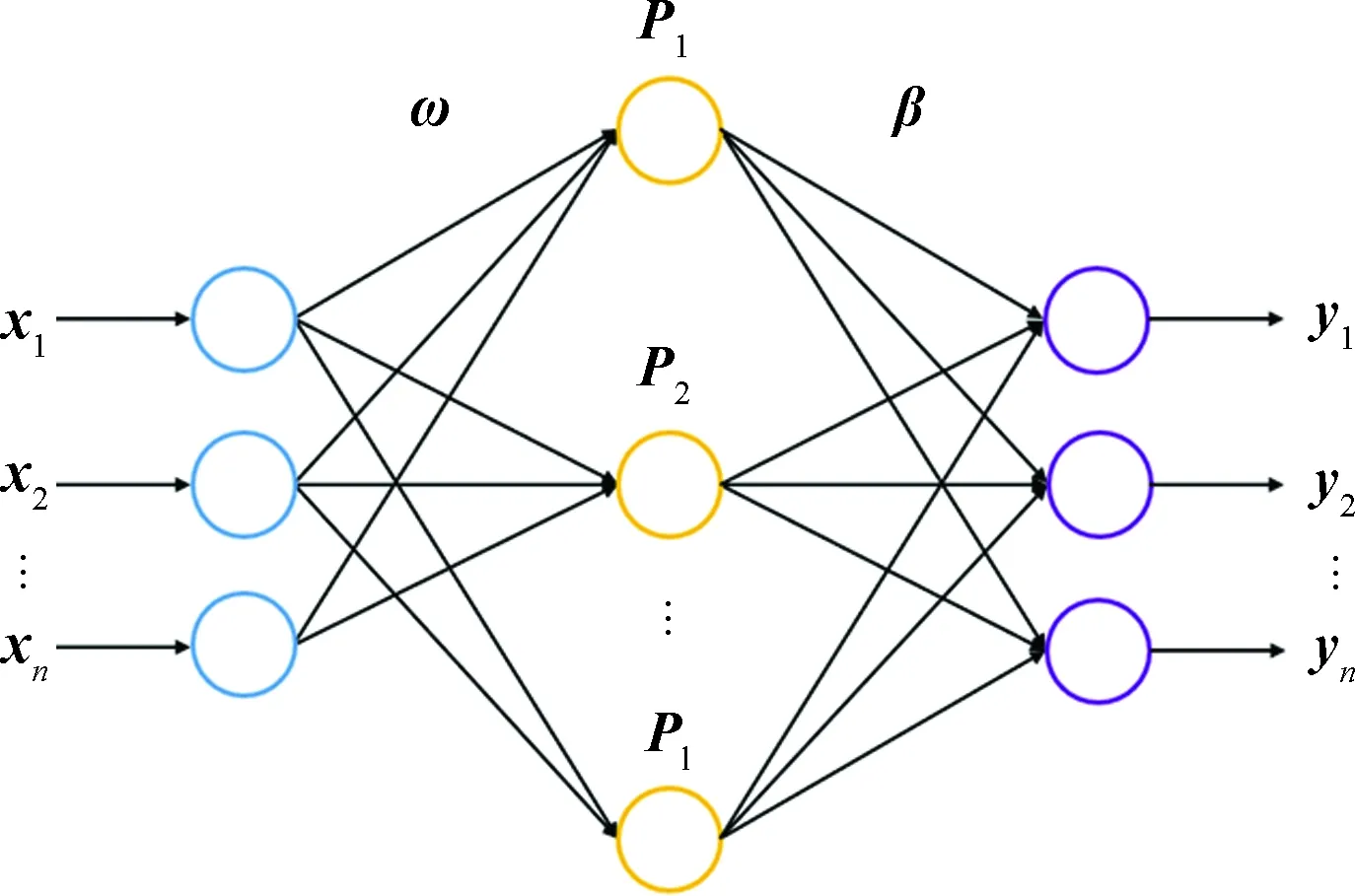
图1 极限学习机网络结构Fig.1 The ELM(extreme learning machine) network structure

1.2 差分进化算法

差分进化算法(DE)适应性强,相较于其他优化算法能够快速收敛,且不易陷入局部最优。其算法流程如图2所示。

图2 DE算法流程图Fig.2 Flowchart of the DE(different evolution) method

1.3 差分进化极限学习机模型

在TSA问题中所采用的DE-ELM的具体步骤如下。

(1)设置ELM以及DE算法的基本参数。

(3)对于每种θ计算中间层输出矩阵

H=

得到输出权重β:β=(HTH)-1HTT,并以暂态稳定评估正确率作为适应度函数。

(4)变异操作、交叉操作、选择操作,生成新一代种群。

(5)重复循环步骤(3)和步骤(4),直到完成算法所需目标。

(6)计算出矩阵H和权值β。

2 基于序列浮动后向算法(SFBS)的特征选择

2.1 初始特征量的选取

基于机器学习方法的暂态稳定评估需要对初始特征进行特征工程,以筛选出评估准确率高、与所解决稳定相关度较大的特征。通过结合以往专家对电力系统稳定性的分析,建立如表1所示23个初始输入特征。

2.2 基于序列浮动后向算法(SFBS)进行特征选择和降维的实现

SFBS是一种特征选择方法,通过结合前向与后向选择来尽可能多地保留任务的有效特征,避免重要特征的冗余和丢失。

SFBS算法首先将全部特征作为初始特征集合S0,此时分类器的识别率作为基准识别A0。第一阶段,在S0中删去特征ai,使得分类器的识别率不小于基准识别率,得到新的特征集合Si和基准识别率Ai,重复此过程直到没有可剔除特征；第二阶段,添加一个已经删去的特征bj到特征集合Si中,使得分类器的识别率大于Ai,得到新的特征集合Sj和基准识别率Aj,重复此过程直到没有可以添加的特征使得识别率大于基准识别率,算法结束,输出最优的特征集合Si。

考虑到电力系统暂态稳定初始特征具有较强的相关性,一定程度上增加了特征集合的冗余,并增加了特征选择的计算量,因此采用具有数据压缩特性的主元分析法(principal component analysis,PCA)进行特征降维,再利用SFBS算法进行特征选择。

表1 初始集合特征量及物理描述Table 1 Features of initial input and its physical description

3 实例验证分析

3.1 样本生成

通过众多专家学者[3-6]采用的暂态稳定评估系统新英格兰10机39节点系统对模型性能进行验证,利用中国电科院PSASP进行如下故障设置:发电机模型选择六阶模型,故障类型选择三相短路,保护在0.2 s时动作,切除故障后系统结构保持不变。分别在4种发电机出力类型,5个负荷水平(80%、 90%、100%、110%、120%)下,60个不同的故障位置进行故障仿真,一共仿真出 1 200组数据集。随机选取900组作为训练样本,其余300组作为测试样本测试验证。

3.2 特征选择结果

为去除变量间单位和大小间的差异同时减少特征的冗余,在特征选择前先对数据进行归一化处理,随后通过主元法降维方法,提取降维后的前13个特征来代表系统总特征,之后再通过SFBS算法进行特征选择,经过多次实验算例分析,最终得到11个特征向量,所选特征如表2所示。

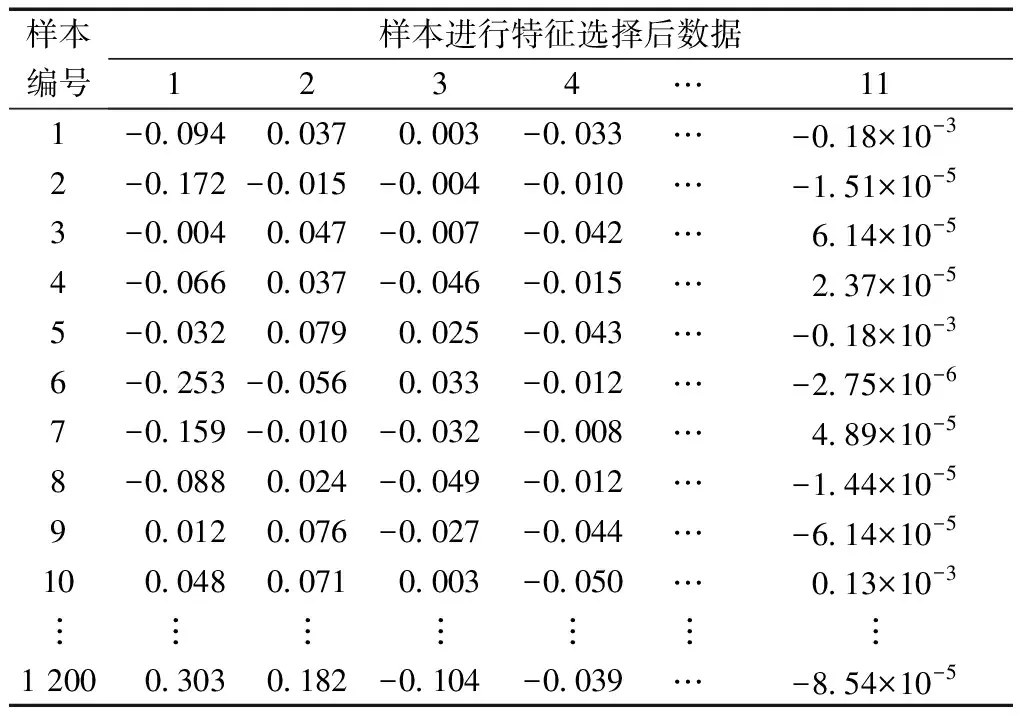
表2 特征降维及筛选后集合Table 2 Features after dimension reduction and selection

3.3 结果分析

为了验证DE-ELM作为分类器的优越性及稳定性,选取未经优化的ELM进行对比；经过PCA降维及SFBS特征选择后特征数减少到初始集合的45.83%,为了验证特征选择的有效性,选取全特征集合作为输入的DE-ELM、ELM和经过PCA降维后未经SFBS特征选择的13个特征作为输入DE-ELM、ELM进行对比,每个模型均进行50次迭代,取50次结果平均值作为比较。设置种群规模NP=200,交叉概率CR=0.8,变异概率F=1,极限学习机隐层节点数均设置为72,结果如表3所示。

表3 优化及特征选择前后评估结果Table 3 Assessment results before and after optimization and feature selection

由表3可知,SFBS-DE-ELM的评估性能最好,达到了98.58%,同时所用特征集也为6种模型中最少,因而验证了SFBS算法对于DE-ELM性能具有提升作用。同时经过对比可以看到,不论是哪种特征输入,DE-ELM均比ELM具有更高的精度,证明了DE-ELM的优越性。同时将DE-ELM与常用算法优化的极限学习机进行正确率与模型训练时间对比,对比结果如表4所示。

通过对比可知,DE-ELM的评估正确率较其他常用算法优化的极限学习机评估准确率最高,体现了差分进化算法的优势,而改进粒子群算法的收敛速度虽然最快,但其评估正确率不如差分进化算法高；遗传算法收敛速度较慢,且评估性能低于改进粒子群算法和差分进化算法。通过对比体现了DE具有较好的收敛能力,且收敛速度较快,算法的时间复杂度较低。对于训练好的极限学习机模型,可在测试阶段直接对测试样本进行分类,分类单条样本时间仅为0.21×10-5s,因此符合暂态稳定评估的快速性要求。

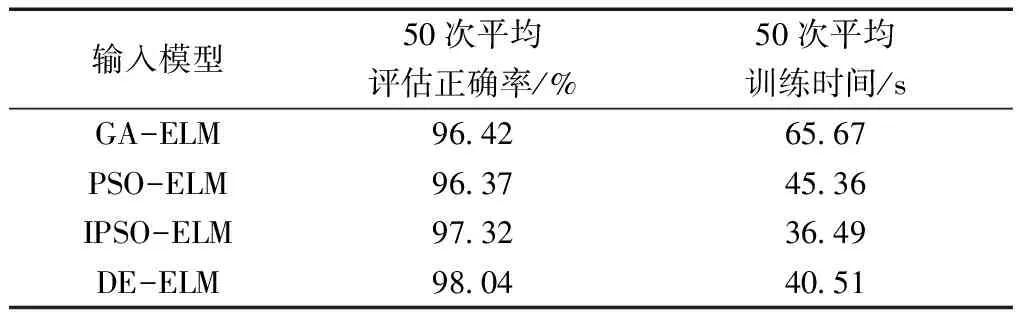
表4 与常用优化模型评估结果对比Table 4 Comparison with the usual optimization models in assessment results

4 结论

针对中外极限学习机在TSA问题中的缺陷,创新地提出将差分进化极限学习机和序列浮动后向特征选择相结合的方法。首先将具有较高相关性的初始特征集利用主元分析降维,再利用序列浮动后向算法进行特征选择,将输入特征压缩到原集合的45.83%,最后将最优集输入差分进化极限学习机进行暂态稳定评估。通过IEEE39节点仿真结果表明:相较未经优化的极限学习机,差分进化优化后的ELM由于其权值和阈值不是随机选取,因而具有较强的稳定性；同时相较其他优化算法,DE收敛速度较快,能够跳出局部最优,因此使得差分进化极限学习机具有最高的分类精度。在此基础上,利用基于SFBS的特征选择在大幅减少了输入特征集的同时,进一步提升了ELM的评估性能。

综上所述,将“差分进化极限学习机”引入电力系统暂态稳定评估,与其他方法相比提升了模型的评估性能,为该问题的解决提供了新方法,具有较好的应用前景。