基于高斯伪谱法的双摆桥式起重机消摆策略分析

刘岩松, 王宗彦, 石瑞敏, 李 松

(中北大学机械工程学院, 山西省起重机数字化设计工程技术研究中心,太原 030051)

双摆桥式起重机(简称双摆桥起)的摆动包括吊具绕大小车的一级摆动与负载绕吊具的二级摆动[1]。出于对工艺要求与安全要求的双重考虑,不仅需要大小车的快速运行来提高工作效率,也需要较小的摇摆角度来进行安全生产。2013年国家能源局修订了新版本的NB/T 20234—2013 规范,对核电厂用起重机的吊具摇摆角度和不同场合的各种核电起重机运行机构的定位精度与速度偏差均做了详细标准规定[2]。为了能够使防摇控制达到最佳的效果,中外各个领域的专家与学者都从不同角度出发,为起重机制定了不同防摇摆策略。

Blajer等[3]把大小车的运行与负载的摆动分开考虑,搭建了两个独立的系统进行研究,然后引入比例-积分-微分环节,成功解决了起重机负载摇摆的问题；Singhose等[4]首次将输入整形的控制方法运用到桥机的防摇摆上,通过对运行过程中的绳长进行变化,最终达到消摆的目的； Toxqui等[5]利用模糊控制PID算法对塔机负载防摆问题进行研究,既减小吊具的摆动幅度又能降低风力、摩擦力等外界不可控因素对性能的影响；耿冲等[6]运用迭代学习理论对双摆桥起的位置和速度进行双重控制,通过迭代学习最终能够按照期望的轨迹与速度进行运动；彭海军等[7]提出了一种动力学模型自变量区间不确定的研究方法,用代理模型对原轨迹规划问题进行代替,取得了令人满意的控制效果。虽众多学者都对相关控制方法进行了研究,并且由于吊具或负载的质量或者体积较大,在研究过程中不能简单地看作质点处理,这使得目前已知方法对起重机进行消摆的效果不是很理想。

针对上述问题,建立双摆桥起的动力学模型和最优控制模型,并把原最优控制问题转化为基于时间最优控制的高斯伪谱形式实现对双摆桥起的消摆策略分析。仿真实验验证所提消摆策略的准确有效性和优越性。

1 双摆桥起模型的建立

1.1 动力学模型

双摆桥起工作过程中,吊具与负载的摆动若超过允许安全极限不仅会降低工作效率,还产生安全隐患。中国国家规定在实际应用中应使吊车系统的两级摆动θ1max、θ2max保持在4°以内,根据图1的双摆桥起二维模型,利用拉格朗日方程法建立其在运行过程中的动力学方程,并运用极小值原理对系统的运动学方程进行简化,模型参数见表1。

(1)

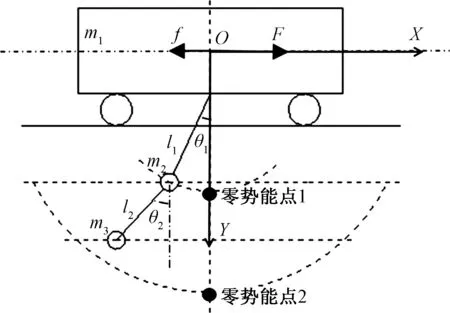
图1 二维简化模型Fig.1 The simplified two-dimensional model

参数物理意义参数物理意义m1/kg大车质量l·2/(m·s-1)负载起升速度m2/kg小车质量θ··1/(rad·s-2)吊具摆角加速度m3/kg负载质量θ··2/(rad·s-2)负载摆角加速度θ·1/(rad·s-1)吊具摆角速度l··1/(m·s-2)吊具起升加速度θ·2/(rad·s-1)负载摆角速度l··2/(m·s-2)负载起升加速度l·1/(m·s-1)吊具起升速度X··/(m·s-2)小车加速度

(2)

根据式(2)选取双摆桥起系统小车的加速度以及绳索提升或下放的加速度作为可实时控制的输入参数,对它们进行二次积分得到系统运动状态。以 QD 型16 t双摆桥起为参照建立数值仿真模型及图2所示的1∶1三维虚拟样机模型,并导入 ADAMS 软件中,通过 ADAMS 软件分析,从而最大限度地模拟双摆桥起真实的工作情况。

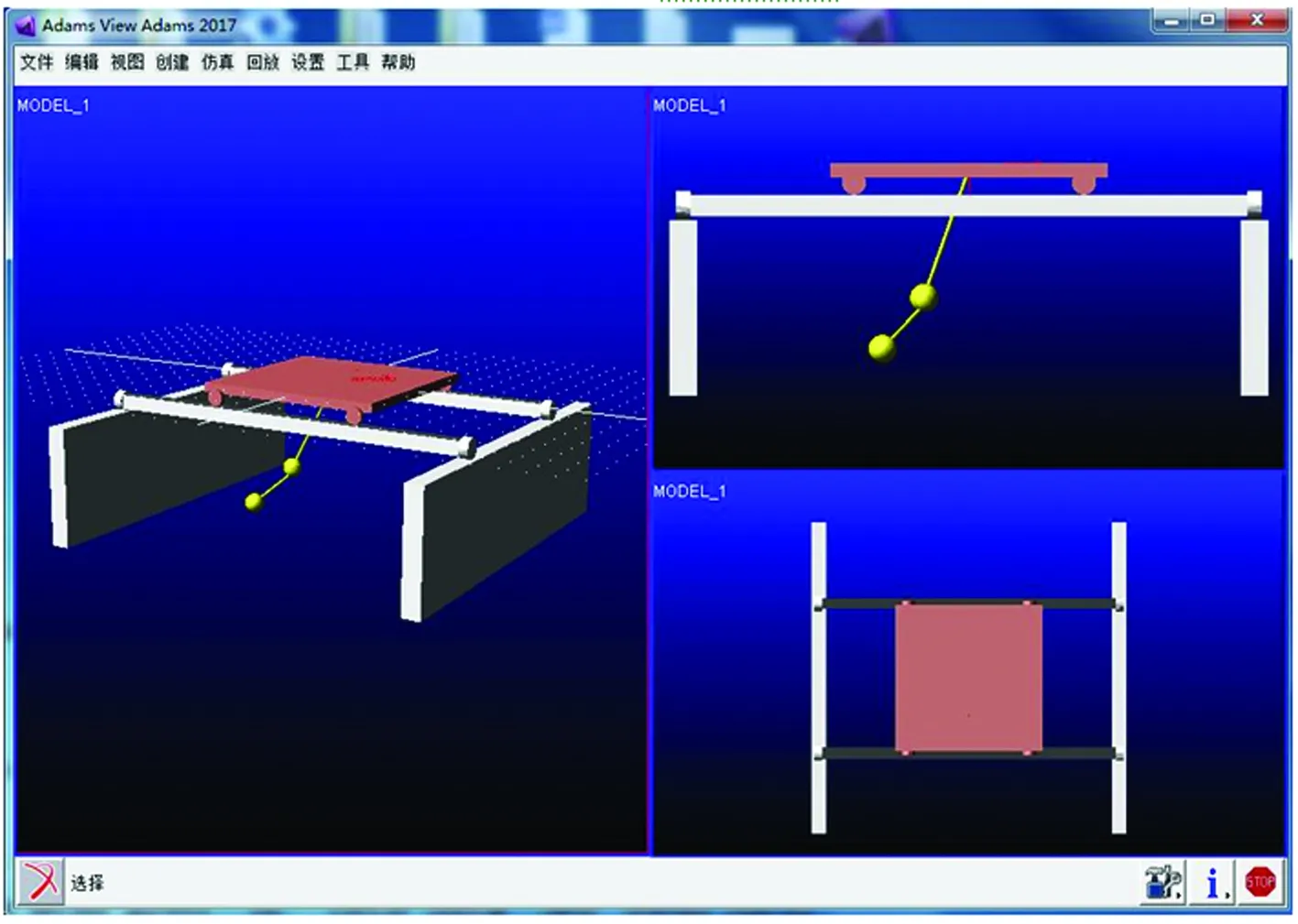
图2 基于ADAMS软件的虚拟样机模型Fig.2 The virtual prototype model based on ADAMS software

针对双摆桥起仿真模型在MATLAB / Simulink软件与 ADAMS 软件中输入相同的运动曲线,可验证该仿真模型与实际系统的相似程度。当给定二者相同的小车与钢丝绳加速度,两个软件输出的吊具和负载的摆动情况见图3。通过比较对应图中的输出曲线可知:各对应曲线无论幅值还是变化趋势都基本一样,因此可以得出结论：此处建立的双摆桥起动力学模型是正确的结论。

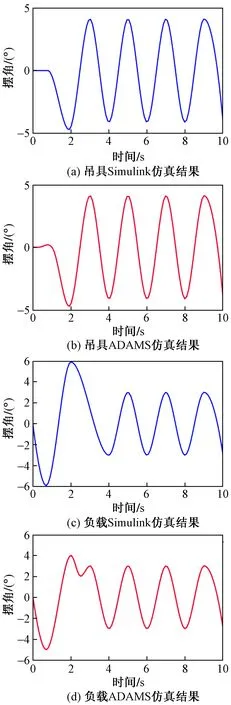
图3 负载摆角仿真结果比较Fig.3 Comparison of simulation results of load swing angle

1.2 最优控制模型

在采用高斯伪谱法对双摆桥起系统的最优轨迹进行实时控制前,需按最优控制理论建立其最优控制模型[8]。

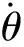
(3)

式(3)中:f(ξ)与b(ξ)为辅助向量与矩阵。

对tf进行求解,即可得到基于有限时间内双摆桥起最优控制问题的最优解为

minJ=Φ(tf)

ξ(tf)=[xf0lf0 0 0 0 0]

u(0)=[0 0]T,u(tf)=[0 0]T

|x(t)|≤L1,|l(t)|≤L2

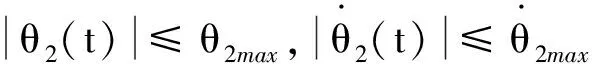
(4)

2 基于高斯伪谱法的轨迹规划

高斯伪谱法是用勒让德多项式通过对函数近似表达的插值理论对各变量以及约束进行表达[9]。目前该方法已广泛应用于航空航天等“高精尖”领域轨迹规划[10]。

针对上述双摆桥起的时间最优控制问题,引用高斯伪谱法把原问题转化为在一系列勒让德点处进行离散的非线性规划问题,使控制系统能够向着快速、精确和稳定的方向发展。与一般求最优解策略的不同之处在于高斯伪谱法能够直截了当的在原模型上进行处理和分析并在有限时间内获得最优解。高斯伪谱法的算法的流程具体见图4。

图4 高斯伪谱法流程图Fig.4 The flow chart of Gauss pseudo-spectral method

2.1 时域转换

在研究双摆桥起防摆的问题时,使用高斯伪谱法对小车与吊具的最优运动轨迹进行求解,需要根据勒让德多项式根的数值特点,把整个系统运行过程中时间坐标的范围由[0,tf]映射至[-1,1],时间变量可通过式(5)进行转化。

(5)

2.2 全局变量的离散与近似

在(-1,1)的范围内选取前K阶勒让德多项式的根PK作为插值节点并组成点列{τ1,τ2,…,τk}。将τ0=-1放至点列的第一位,则各个时间点的状态变量与控制变量的表现形式为

(6)

在以上K+1个插值节点处,构造出拉格朗日插值多项式进行插值,具体可表示为

(7)

(8)

通过式(6)～式(8)可得到的系统状态向量和控制向量的离散值,系统状态与控制变量的轨迹能表示为

(9)

式(9)中:Y(τ)与U(τ)表示在任意时刻τ时系统的状态变量与控制变量的近似值。

2.3 动力学约束方程的近似

对式(9)中经过离散的状态向量轨迹进行求导,可得到系统离散后的动力学微分方程为

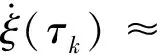
(10)

(11)

根据式(10)和式(11)以及系统实际运行过程中各变量的实时数据,可对最优控制问题中的动力学约束方程进行离散化与近似化处理，结果为

(12)

式(12)中：k∈{0,1,…,K}。经过调整后最优控制问题中的微分约束即可变化为代数约束。

2.4 终端约束的高斯伪谱转化

为了将整个问题转变为非线性规划问题,最优控制问题在边界处的约束也需转变为代数约束,其中系统在起始位置的状态可直接由向量ξ(0)表示为

ξ(0)=[0 0L20 0 0 0 0]T

(13)

当τ=1时,此时小车与起升系统都位于最终位置,所以τK+1=1。利用高斯求积公式可将系统结束时刻的边界条件标记为

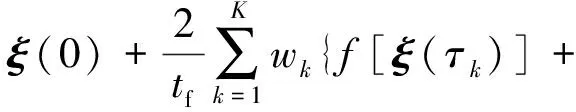
b[ξ(τk)]u(τk)}

(14)

式(14)中：wk为勒让德权值。

2.5 双摆桥起最优控制问题的NLP形式

经过以上步骤,最优控制问题中的所有约束已转变为代数约束,原问题也转化为一种具有代数约束的非线性规划问题。

mintf

b[ξ(τk)]u(τk)}=0

ξ(τ0)=[0 0L20 0 0 0 0]

b[ξ(τk)]u(τk)}=ξ(τK+1)

ξ(τK+1)=[xf0lf0 0 0 0 0]

ξ(τ)-γ≤0,-ξ(τ)-γ≤0

u(τ)-ζ≤0,-u(τ)-ζ≤0

(15)

式(15)中:向量γ与向量ζ的具体形式为

(16)

ζ=[a1maxa2max]

(17)

对于上述带约束非线性规划问题采用连续二次型规划方法(SQP)求解[11],可得

ξ(τ0),ξ(τ1),ξ(τ2),…,ξ(τK),ξ(τK+1)

(18)

式(18)为时间最优状态向量序列,分别对序列中各向量的前四项(小车位移、速度及钢丝绳长度、起升/下降速度)进行拉格朗日插值,进一步得出有限时间内小车和起升系统的位移与速度轨迹。

3 仿真与实验

为验证高斯伪谱法计算得到的轨迹适用性和准确有效性,对上述计算的连续双摆起重机动力学约束、边界条件以及末段状态等相关参数,使用 GPOPS-II 软件工具箱与 fuzzy 软件工具箱对双摆桥起从起吊—运行—放钩的全过程进行仿真计算,并与现有其他控制防摇摆的方法进行对比。

3.1 参数改变的对比仿真

为得到不同仿真参数下双摆模型的摇摆时间以及摇摆情况,需先对双摆起重机模型的初始参数进行设置,初始参数设置如表2所示。

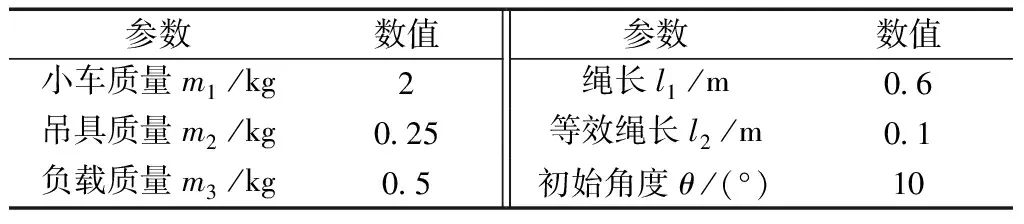
表2 初始参数设置Table 2 The initial parameter settings

3.1.1 不同绳长的对比仿真

在其他数值相同的情况下,将绳长l1分别设为0.6、1、2.4 m进行对比仿真。不同绳长下,θ1与θ2随时间变化的结果见图5。

图5 不同绳长时摆角变化的对比Fig.5 Contrast in pendulum angle variation of different rope length

由图5可知:吊具分别经过3、3.6、4.1 s后保持静止,负载分别经过3.3、3.8、7.8 s保持静止。虽然随着钢丝绳长度的增加,吊具与负载的摆动时间也逐渐变长,但二者都可在两个周期内保持静止,该对比分析结果说明了不同绳长下高斯伪谱法消摆的适用性。

3.1.2 不同负载质量的对比仿真

将绳长负载质量分别设为0.5、1、1.5 kg进行对比仿真。当负载质量不同时,摆角θ1与θ2随时间变化的结果见图6。

图6 不同负载质量时摆角变化对比Fig.6 Contrast in pendulum angle variation with different load mass

由图6可知:虽然随着负载质量的增加,负载与吊具消摆所需要的时间以及两者最大幅度都将略微增加,但是摆动角度都是在安全极限范围内变化,且消摆时间也都在两个周期以内。证明了所制订的消摆策略在负载质量不同的情况下,能够满足实际工况下的消摆需求。

3.1.3 不同初始角度的对比仿真

为了考察当初始角度不同时,从开始摇摆到最终静止的时间是否会发生变化,将初始角度分别设为5°、10°、20°进行对比仿真。当初始角度不同时,θ1与θ2随时间变化的结果见图7。

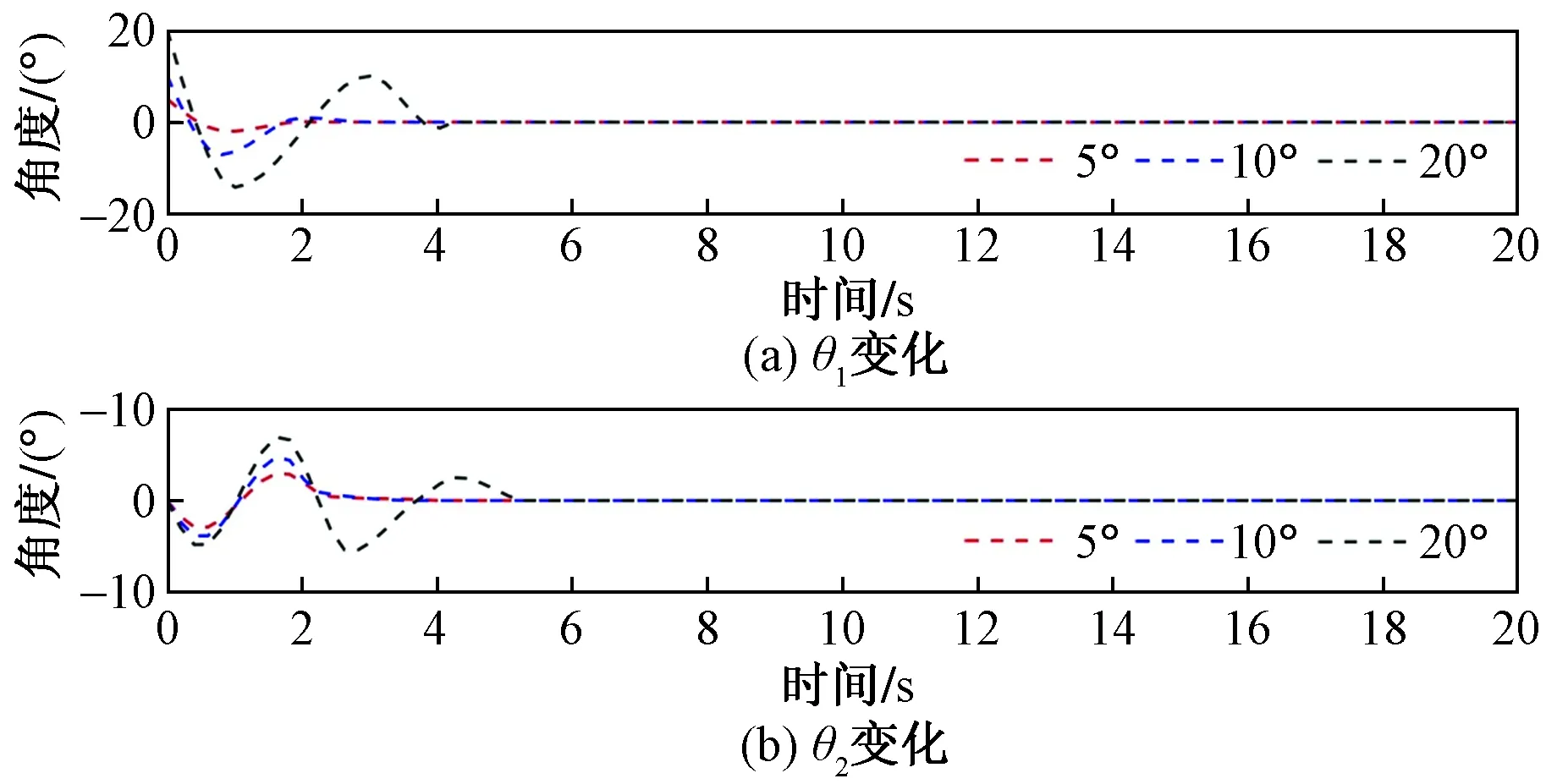
图7 不同初始角度时摆角摆角变化对比Fig.7 Contrast in pendulum angle variationat different initial angles

由图7可知:随着初始角度的增加,消摆所需要的时间虽然也在逐渐增加,但二者均能在能在两个周期之内快速实现消摆,验证所制订的高斯伪谱法消摆策略在初始角度不同的情况下均有良好的控制效果。

3.2 与模糊 PID 算法的对比仿真

通过分析可知小车驱动力与起升系统的拉力是抑制双摆桥起摆动的关键,通过不断地改变两者的大小,实现对小车的水平位置以及负载与吊具的垂直位置进行控制,以此限制负载的摆动幅度。但不同的算法实现该过程的方式却不尽相同。

为进一步验证高斯伪谱法的适用性和优越性,在进行模拟仿真时,小车将分别使用模糊 PID 算法与高斯伪谱法进行控制,并且在系统上进行多次仿真以减少数据的偶然性。仿真过程中输入的其他参数参照表2。

在实验参数相同的情况下,当用上文提到的两种方法分别对小车进行控制,图8为小车位移、速度以及加速度的实时控制曲线,图9为吊具与负载角度与角加速度的实时曲线。

由图8(a)与图8(b)可看出:在未超过位移极限与速度极限的前提下,两种控制方法都能使小车精准地到达目标位置,但高斯伪谱法曲线更加平缓与稳定,使用的时间为4 s左右,模糊 PID 使用的时间为6 s左右。

图8 小车位移、速度和加速度的实时控制曲线Fig.8 Real-time control curve of displacement, speed and acceleration of the crane trolley

由图8(c)可看出:相比于高斯伪谱法,模糊 PID 控制方法下小车的初始加速度超过了所研究的 QD 型双摆桥起能提供的加速度极限。当本方法已经使小车保持稳定后,模糊 PID 控制方法仍有轻微的残余震荡。

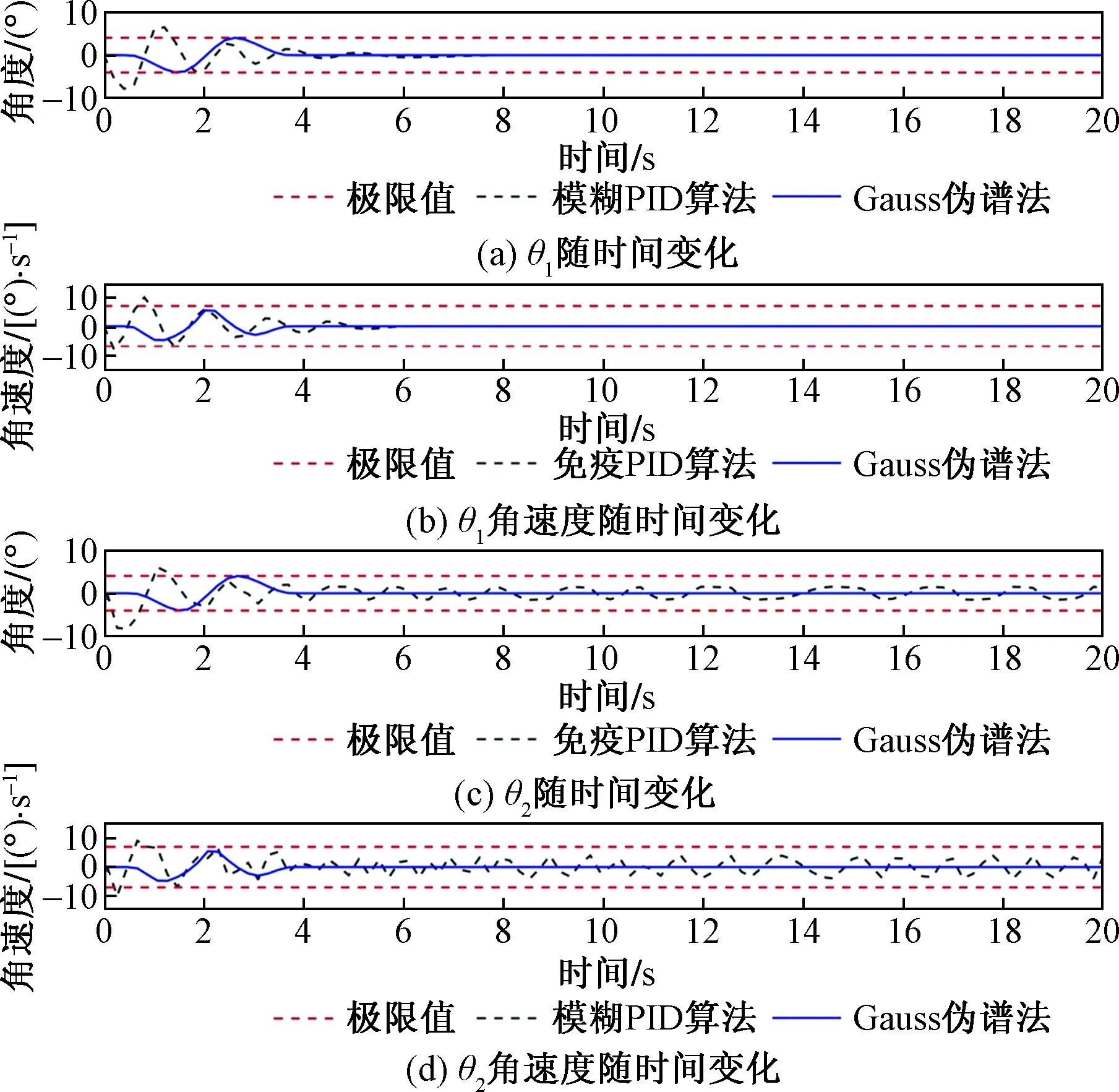
图9 摆角随时间变化曲线Fig.9 The pendulum curve angle variation with time

由图9(a)与图9(b)可看出:采用高斯伪谱法进行消摆研究的模型其吊钩在到达稳定状态后无残余震荡,全程未超过规定的摇摆极限；而使用模糊 PID 控制方法时吊钩稳定需要7 s左右且最大摆动角度与角速度均超过规定的摇摆极限。

由图9(c)与图9(d)可看出:使用高斯伪谱法进行消摆研究的负载摆动的角度与角速度更加平缓,全程未超过规定的摇摆极限；而使用模糊 PID 控制方法时负载最大摆动角度与角速度均超过规定的摇摆极限,产生了猛烈的残余震荡且在20 s的采样周期内,负载未达到静止状态。

综合分析仿真结果可知:高斯伪谱法能在双摆桥起运行过程中实现小车的精准定位并实现负载与吊具的快速消摆,符合理论分析；虽然模糊 PID 控制方法也能对负载与吊具的摆动起到一定的抑制作用,但与高斯伪谱法相比,个别参数不仅超过了系统允许的最大值,在控制时间上也不尽如人意,且在小车静止后吊具与负载均产生了不同程度的残余震荡。在两种方法控制的过程中,各参数是否能够满足系统的极限要求如表3所示。

高斯伪谱法相比于模糊 PID 控制方法各参数的性能提升比率如表4所示。

表3 两种方法极限对比较Table 3 Limit comparison for the two methods

表4 两种方法性能对比Table 4 Performance comparison of the two methods

4 结论

综合考虑系统本身影响因素以及一系列约束条件,建立了双摆桥起运动学模型和基于时间的最优控制模型。采用高斯伪谱法得到基于时间最优控制的双摆桥起高斯伪谱形式。利用GPOPS-Ⅱ软件包对不同参数下高斯伪谱法防摆效果进行仿真,证明了所用的高斯伪谱法在不同重量负载、不同绳长以及不同起始角度的情况下,对双摆模型均有较好的控制作用；将求解结果与基于模糊 PID 控制算法进行比较,证明了高斯伪谱法解决双摆问题的卓越性,且控制效果明显优于普通算法。