基于拓扑空间的C字符串函数缺陷分析

龚萌晓, 谢惠扬

(北京林业大学 理学院,北京 100083)

0 引 言

C语言是一种应用广泛的计算机语言,其功能丰富、使用灵活、可移植性好[1]。但是C语言的语法检查不是很严格,一些未定义的操作结果若不注意使用则容易出现错误,且也容易出现编译正常却运行异常的情况[2]。文献[3]详细列举了C语言的诸多缺陷,这些问题可能会影响数据的安全性,造成内存的占用,甚至会导致系统崩溃等。文献[4]对不同编程语言存在的漏洞进行了分类。文献[5]将使用C语言开发程序时存在的漏洞分为5种,并分析产生漏洞的原因,进而提出利用漏洞实施的攻击和缓解漏洞的技术。因此，研究C语言的缺陷,从而避免缺陷和漏洞的产生尤为重要。

拓扑学、代数学和分析学被认为是基础数学的三大领域[6]，拓扑学在计算机科学方面的应用主要是在图像处理和图论基础等方面[6]。目前，新兴的拓扑数据分析(topology data analysis,TDA)已成为研究的热点。本文拟用拓扑学分析C语言中字符串函数缺陷,运用拓扑学解决C语言程序缺陷是一种新的方法，需要借鉴拓扑学在其他领域里的应用。很多针对拓扑学的应用往往得不到定量的结果,仅仅是定性分析。

1 C语言字符串缺陷函数示例

在C语言编程中,字符型数据并不是以字符形式存储在内存中,而是以字符的整数形式存在存储单元中,且大多数操作系统采用ASCII字符集编码[1]。C语言中没有字符串类型的变量,如果要将一个字符串存放在内存中,那么需要使用字符数组进行操作[1]。虽然编译系统提供的字符串库函数给用户带来了极大的便利，但是字符串函数运行过程对变量不做边界长度检查却造成了许多缺陷。尤其在大型的编译代码中 稍有差错便不能得到正确的输出结果,更为严重的是会产生内存问题[7]。由于C语言对变量不做边界检查,代码在一定程度上会造成缓冲区溢出,从而难以得到正确的输出结果,这就是最为典型和常见的缓冲区溢出漏洞[8]。

下面给出2个缺陷函数的示例代码。

(1) 示例代码1。strcpy函数溢出缺陷示例代码为：

#include〈stdio.h〉

#include〈string.h〉

int main()

{

chars1[10];

chars2[20]=“the source string”;

strcpy(s1,s2);

}

strcpy为string copy(字符串复制)的缩写,其作用是将字符数组s2存储的字符串复制到字符数组s1中[1]。这里要求s1定义的长度足够大,以使s1能够容纳s2中的字符串。编程人员有时将s2直接定义为常量,但是因为strcpy函数不检查字符串长度,所以容易出现错误。在示例代码1中s2中的字符串“the source string”的长度大于10,但是s1的长度只是10,因此s1的长度不能够容纳s2中的字符串,复制后便造成缓冲区溢出。

(2) 示例代码2。strcat函数溢出缺陷示例代码为：

#include〈stdio.h〉

#include〈string.h〉

int main()

{

chars1[20]=“the string1 and”;

chars2[10]=“string2”;

strcat(s1,s2);

}

strcat函数为string catenate(字符串连接)的缩写,作用是将字符数组s2的字符串连接在字符数组s1的字符串后面,然后把结果存放在字符数组s1中[1]。此处同样要求s1定义的长度足够大,以使s1能够容纳连接后的新字符串。示例代码2中s1和s2连接后的字符串“the string1 and string2”的总长度超过分配给s1的长度20,说明分配给s1的长度不足，这便造成缓冲区溢出。

由2个示例代码可见,使用字符串函数时应当对字符数组定义足够大的长度,以便字符数组能够容纳处理后的新字符串[9]，C语言在编译过程中不会给出错误信息,因而一旦运行往往很难得到理想的输出结果[10]。对于大型的编程文件来说,出现一点小的错误,结果却可能千差万别,甚至容易被黑客利用，造成具有危害性的结果[8]。

2 拓扑空间有关定义

点集拓扑学与其他的几何学相比,更具有灵活性和可塑性。点集拓扑学中应用最频繁的特性可归纳为“3个C”:连续性(continuous)、连通性(connectedness)和紧致性(compactedness)[6]。通过点与集合构造拓扑空间的结构,并考查拓扑空间中的不变性质是拓扑学应用的关键之一。本文主要根据其具有连续性特点分析问题。

定义1[11]设X是一个集合,T是X的一个子集族,如果T满足如下条件:

(1) ∅,X∈T。

(2) 若A,B∈T，则A∩B∈T。

(3) 若T1⊂T,则∪A∈T1A∈T,称T是X的一个拓扑。如果T是集合X的一个拓扑,那么称偶对(X,T)是一个拓扑空间,或称集合X是一个相对于拓扑T而言的拓扑空间,简称集合X是一个拓扑空间。此外T中的每一个元素为拓扑空间(X,T)或X中的一个开集。

定义2[11]设X和Y是2个拓扑空间,映射f:X→Y,如果Y中每个开集U的原像f-1(U)是X中的一个开集,那么称f是X到Y的一个连续映射。

定义3[11]设(X，T)是一个拓扑空间,x∈X,如果U是X的一个子集,并满足条件:存在一个开集V∈T使得x∈V⊂U,那么称U是点x的一个邻域。点x所有邻域构成的X子集族被称之为点x的一个邻域系。

定理1[11]如果U是包含着点x的一个开集,那么它一定是点x的一个邻域。

定义4[11]设X是一个拓扑空间,A⊂X。如果点x∈X的每一个邻域U中都有A中异于x的点,即U∩(A-{x})≠∅,那么称点x是集合A的一个凝聚点。集合A的所有凝聚点构成的集合称为A的导集,记为d(A)。

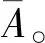
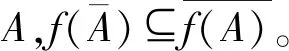
3 基于拓扑空间的缺陷检测

一般地,拓扑学往往用于对问题进行定性分析[6]。本文将通过映射的连续性分析C语言中字符串函数的溢出缺陷。

3.1 字符串函数的拓扑刻画

定理3 令C语言代码chars[n+1]中的s是一个赋初始长度为n+1的字符数组,s[0]～s[n]是s的n+1个数组元素。如果X为所有数组元素s[i]中存储的字符为元素构成的集合,其中0≤i≤n(若实际字符串长度小于n,那么默认令终止符后面的字符元素为空);如果Tx为数组元素s[0]～s[j]中存储的字符为元素构成的集合,其中0≤j≤n;那么Tx是X的一个子集族,而且Tx是X的一个拓扑,偶对(X,Tx)是一个拓扑空间。

证明由X和Tx的形式可知:

(1) ∅∈Tx,当j=n时，可得X∈Tx。

(2) 若A,B∈Tx,设A表示s[0]～s[i]中存储的字符为元素构成的集合，B表示s[0]～s[j]中存储的字符为元素构成的集合,其中0≤i≤n,0≤j≤n,则有i≤j或j≤i成立。当i≤j时，A⊆B,A∩B=A∈Tx；当j≤i时，B⊆A,A∩B=B∈Tx,故有A∩B∈Tx。

(3) 若T1⊂Tx,由(2)中的讨论可知∪A∈T1A表示T1中存储字符元素数目最大的那个字符元素集合,则∪A∈T1A∈T1⊂Tx,因此有:

∪A∈T1A∈Tx。

Tx满足定义1中的3个条件,因此由定义1可知,Tx是X的一个拓扑,偶对(X,Tx)是一个拓扑空间,Tx中的每一个元素就是X中的一个开集。

例1C语言代码为chars[10]=“string”,则该语句的结构如图1所示。

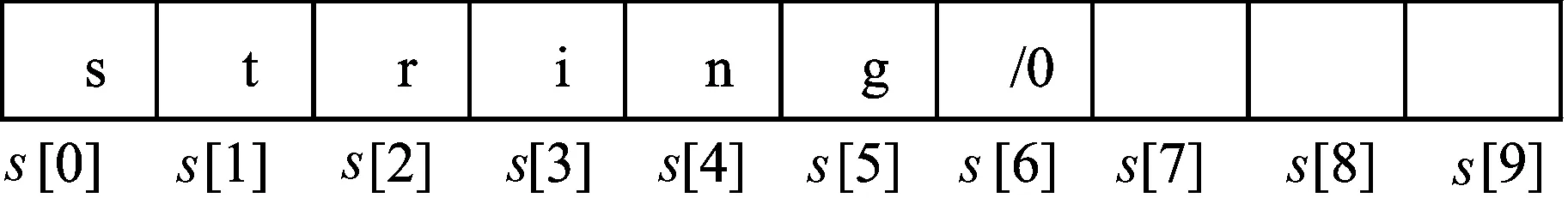
图1 C语言代码为char s[10]=“string”的结构

X={s,t,r,i,n,g}，

Tx={∅,{s},{s,t},{s,t,r},{s,t,r,i},{s,t,r,i,n},{s,t,r,i,n,g}}。

为了不引起混淆,定义使用[s[i]](0≤i≤n)表示数组元素s[i]中存储的字符元素，则有拓扑空间X={[s[0]],[s[1]],…,[s[n]]},定义的拓扑Tx={∅,{[s[0]]},{[s[0]],[s[1]]},…,{[s[0]],[s[1]],…,[s[n]]}}。

对于点x∈X,不妨设x={[s[i]]}(0≤i≤n),令U={[s[0]],[s[1]],…,[s[i]]},由此可见U∈Tx,则U是X的一个开集,且x∈U,由定理1可知,U是x的一个邻域。此外,由定义3中邻域的定义可知,需要存在一个开集V∈Tx满足x∈V⊂U,由定理3中Tx的形式可以看出包含x的开集V的形式,这说明点x=[s[i]]的最小邻域的形式为U={[s[0]],[s[1]],…,[s[i]]}。

设子集A⊂X和点x∈X，当A为单点集时,设A={[s[i]]}(0≤i≤n),存储在数组元素s[i]中。当点x为在[s[i]]之前的字符元素时,A-{x}={[s[i]]},x的其中一个邻域U={[s[0]],[s[1]],…,[s[i-1]]}满足U∩(A-{x})=∅,由定义4可知,这些点x不是A的凝聚点。

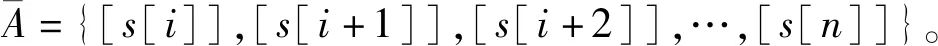
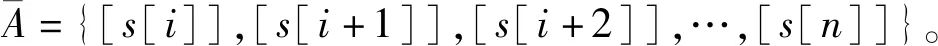
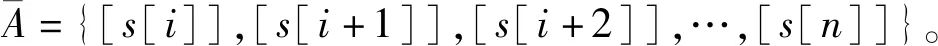
综上所述,可得定理4。

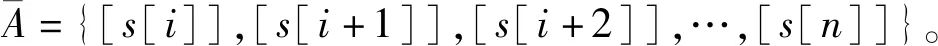
C语言代码chars1[n1+1]和chars2[n2+1]中的s1和s2是2个字符数组,把s1和s2中存储的字符为元素构成的集合看作定理4中定义的拓扑空间,分别记为拓扑空间X1和X2,对应的拓扑分别记为Tx1和Tx2。假设s1和s2初始赋值的字符串长度分别为m1+1和m2+1(m1≤n1,m2≤n2),其中,s1[m1]和s2[m2]分别存储字符串的终止符。下文拟利用映射的连续性进行缺陷检测。

3.2 strcpy函数缺陷检测

对于示例代码1中的代码strcpy(s1,s2),利用strcpy函数将s2中字符串内容复制到s1中。定义同名映射strcpy表示strcpy(s1,s2),由strcpy函数的意义可知,映射strcpy:X2→X1,其逆映射记为strcpy-1。

定理5在代码没有缺陷的情况下,strcpy映射是一个连续映射。

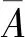
由定理5可知,当strcpy映射不是一个连续映射时,代码是存在缺陷的。如果∃A∈Tx1,当strcpy-1(A)∉Tx2时,即存在X1中的一个开集,其原像不是X2的开集,那么由定义2可知,strcpy不是一个连续映射。此时在拓扑空间中不能够保持开集的不变性,说明代码是存在缺陷的,不能输出正确的复制结果。

对于示例代码1,s1定义了10个数组元素,在代码没有缺陷的情况下,即当s2中的字符元素数目不大于10时,strcpy映射是一个连续映射。此时对于任意0≤i≤9,有[s1[i]]=[s2[i]],代码可以正常地复制字符串并且一对一输出正确的复制结果。如果至少存在一个0≤i≤9使得[s1[i]]≠[s2[i]],即存在X1中的一个开集A={[s1[0]],[s1[1]],…,[s1[i]]}∈Tx1,但是A的原像strcpy-1(A)≠{[s2[0]],[s2[1]],…,[s2[i]]},从而有strcpy-1(A)∉Tx2,那么strcpy映射不是一个连续映射,代码存在溢出缺陷。

3.3 strcat函数缺陷检测

对于示例代码2中的代码strcat(s1,s2),利用strcat函数将s2中字符串内容连接在s1后面。定义同名映射strcat表示strcat(s1,s2),由strcat函数的意义知,映射strcat:X2→X1,其逆映射记为strcat-1。

定理6 在代码没有缺陷的情况下,strcat映射是一个连续映射。

由定理6可知,当strcat映射不是一个连续映射时,代码是存在缺陷的。如果∃A∈Tx1,当strcat-1(A)∉Tx2时,即存在X1中的一个开集,其原像不是X2的开集,那么由定义2可知,strcat不是一个连续映射。说明存在溢出缺陷,连接后的字符元素个数超过初始定义的字符数组长度。

对于示例代码2,s1定义了20个数组元素,在代码没有缺陷的情况下,即当s1和s2赋值的字符元素数目之和不大于20时,strcat映射是一个连续映射,此时代码可以正常地连接字符串并且输出正确的结果。如果存在X1中的一个开集A={[s1[0]],[s1[1]],…,[s1[i]]}∈Tx1,但是A的原像strcpy-1(A)≠{[s2[0]],[s2[1]],…,[s2[i]]},从而strcpy-1(A)∉Tx2,那么strcat映射不是一个连续映射,代码存在溢出缺陷。

4 结 论

本文运用点集拓扑学分析了C语言存在的缺陷。本研究的具体创新性主要有2个方面: ① 本文将点集拓扑学和C语言缺陷检测结合起来,运用拓扑学分析了C语言存在的缺陷；② 本文从2个字符串处理函数入手,构造拓扑空间和空间之间的连续映射,利用拓扑空间的连续性发现2个C语言字符串函数的缺陷。揭示了2个C语言字符串函数的缺陷。

本文仅限于使用连续性解决字符串函数中由于长度分配不足造成的缓冲区溢出缺陷,并考虑能否应用定理3中的拓扑结构解决C语言中存在的其他缺陷。另外,还考虑了能否利用拓扑空间的连通性、紧致性等性质来判定C语言中是否存在缺陷。