数学深度教学的课堂要素
2020-02-22左浩德郭婵婵
左浩德?郭婵婵

摘 要 为扎实理解的教学(Teaching for Robust Understanding,简称TRU)项目基于培养学生深刻理解数学思维的目的,将高效课堂的基本属性总结为数学内容、认知需求、公平获得、身份认同感,以及形成性评价等五个维度。TRU的课堂评价和改进工具有助于一线教师改善课堂教学。
关键词 TRU 数学课堂 深度教学
一、引言
深度教学是培养学生数学核心素养的重要途径,重视引导学生更清晰、深入、全面、合理的思考[1]。数学课堂是师生互动最多的情境,如何在其
中渗透深度教学的理念是需要关注的重要问题。关于数学课堂教学的理论成果汗牛充栋,但高深理论难以融入实际教学仍是常见难题。数学课堂教学的形式化、模板化导致了“为深度而深度”、“表面上热闹,实际没有收获”的现状。因此需进一步审视数学深度教学需要什么样的课堂、怎样以友好方式让一线教师将深度教学理念渗透在数学课堂中。
培养学生数学核心素养的目标是使学生惯用数学思维来思考,有深度的数学课堂教学应更注重 “如何做”“为什么”,而非简单机械的“是什么”。深度教学的理念与美国学者Alan Schoenfeld发起的为扎实理解的数学教学(Teaching for Robust Understanding in Mathematics,简称TRU-Math)研究不谋而合[2]。该项目探究了数学教学应重点关注什么,怎样的课堂环境能帮学生成为淵博灵活的思考者和学习者,教师如何创造更有效的课堂环境等方面的问题[4],从数学教学的目标(Why),有效课堂的要素(What),教师或教育研究者如何使用(How)等三个维度提供了有效数学课堂教学的框架。
尽管有学者已介绍了TRU的框架以及评分标准[3],Schoenfeld本人于2018年也在第三届华人数学教育大会(上海)中做了相关报告,但该框架依旧被我国的一线教师冷落。TRU在数学课堂教学理念和实践等层面都体现了深度教学的目标,有助于改善数学课堂教学,因此本文将介绍TRU的目标、框架和工具,以期提供有价值的参考。
二、TRU的目标——数学深度教学
能够使所有学生在数学课堂上有机会掌握丰富的数学知识、能够灵活地数学地思考,是TRU项目的研究目标。TRU框架认为学生学习数学并不是对知识或步骤的记忆、重复和演练,因此,数学课堂教学不能满足于灌输给学生一系列数学知识或步骤的表面功夫,而应达到使学生理解各个概念或主题背后的联系、数学学科的基本思想之深度。这体现了深度教学的宗旨——让学生在课堂中体验像数学家一样思考的过程。
深度教学首先需要教师对数学知识的深刻理解。教师关于“学生应该怎样理解数学”的观点,很大程度反映在课堂教学的目标和实施过程中[5]。因此,教师在授课前就应深入思考数学中各个主题之间的互相联系和基本思想,除此之外,还需要对学生的学习心理有较好的把握。在此前提下,TRU研究提出深度课堂教学的五个维度,包括数学内容、认知需求、公平获得、归属感和身份认同感,以及形成性评价[6]。TRU遵循培养学生用数学思考的原则,刻画了数学深度课堂教学。从综合的角度来看,如果课堂教学能够按照这五个维度去设计或实施,那么学生在这样有深度的学习环境下,将成为有学识、灵活和机智的思考者和学习者。从分析的角度来看,每个单独的维度都是教师专业发展中应关注的焦点,在教师教育过程中,应专注于系统地改进每个维度。那么,怎样阐释这些维度的含义?如何将其应用于教学?以下将就这两个问题具体分析。
三、TRU框架——有效课堂的要素
在数学课堂中进行什么样的活动才能发展学生的数学能力?TRU认为优秀的深度课堂教学在以下五方面为学生提供了好的学习环境,即数学内容,认知需求,公平获得,归属感和身份认同感,以及形成性评价。需要明确的是,TRU框架并不规定深度课堂中应该发生什么,因为教学无定法。TRU的五个维度仅提供有效课堂的参考和方向。
1.数学内容
赋予学生数学思维是TRU的主要目标,学生在课堂上应体验到连贯的、将有意义的解题过程和步骤符号化了的数学,而不是一系列被用来背诵的彼此孤立的事实、步骤和概念。例如,直角坐标系下直线的方程可表示为y=kx+b;Ax+By=C;
x/a+y/b=1,y-y0 / x-x0=m这几种线性关系的不同形式,分别表示已知直线的任意两个信息就可以决定其位置,互相之间能自由转换。数学教学中需用联系的观点看待以突出知识的连贯性。这反映了深度教学从“知识点”走向“知识结构”的基本理念[7]。
知识问题是深度课堂教学中的关键,“知其所以然”的课程内容是必要前提。将数学知识作为需要死记硬背的步骤来教学,会导致学生的知识停留在浅层,思维固化等后果[8]。TRU提倡使数学知识深入而重点突出、具有连贯性和准确性,帮助学生理解数学实质。
2.认知需求
教师在帮助学生处理任务时不能削弱重要的数学内容,深度的数学课堂需满足学生的认知需求。为此需找到平衡点,教师既能让学生明白自己遇到了什么问题,又留下独立思考的空间。深度教学的实现需经历问题解决、知识运用、开拓创新的过程,如果教师将数学知识“填鸭”似地教给学生,则不能使学生深刻理解数学或形成良好的数学思维习惯。
3.公平获得
该维度聚焦于数学课堂活动是否能使学生都参与有意义的实践。学生所获数学成就的高低与他们的学习机会有关[9]。学习机会差异的一个主要来源是教师讲授知识的不同方式,即课堂教学的不同深度。在数学课堂中谁有机会真正参与到数学活动?所有学生都常有机会讨论数学观点吗?每个学生都有锻炼或者展示自己的机会吗?每个学生都能用现有的知识理解遇到的问题吗[6]?好的教师会选择并设计一些任务的切入点,鼓励所有学生参与到挑战性的数学活动中[10]。
4.身份认同感
TRU框架的第四方面涉及学生的数学气质和自我认同(Mathematical Dispositions and Identities),包括态度、信心、毅力、对数学的认识等。许多学生持有错误或消极的信念,如数学是被记忆而不是理解的,自己不擅长数学等[11]。深度教学关注学生的情感体验,使学生在数学上认同自己,成为积极的数学思维者。
数学自我认同包括两个方面,第一是自主性(agency),即个体做数学的意愿,源于认識到自己面对挑战时取得的进展和对自己所得结论的信心。第二是权威性(ownership),指的是个体对自己推导的数学学科思想的自信。在赋予学生身份认同感的课堂中,教师能发现每个学生的优势并借此帮助学生参与到学习共同体中去。
5.形成性评价
形成性评价引发学生的思考和回应,重视出现的误解,并要求教师有目的地设计任务以评估学生的理解程度,再利用这些信息塑造课堂活动[12,13]。教师在评估学生理解程度的同时也得到了改良教学方式的机会,其后续问题、任务以及“下一步如何做”都是为了更深层次的课堂教学目标。此过程中教师关注学生的理解,因材施教式地教学,就可形成“更清晰、更关注重点和更有效的”深度教学课堂了。实施形成性评价时,学生会被要求在反思中表达自己的想法和收获,这将使学生理解更透彻并将新旧知识相联系。
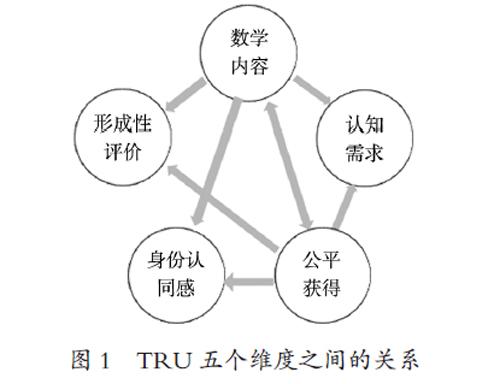
TRU框架全面概括了深度数学课堂应具备的属性,五个维度彼此紧密联系成一个整体,共同作用于挖掘教师数学教学的深度,以及学生思考能力的清晰、深入、全面、合理,如图1。
数学内容的选择决定了是否满足学生的认知需求,形成性评价是否具有好的切入点。公平获得保证每个学生的数学身份认同感,认知需求以及恰当的形成性评价确保了参与的意义。
四、TRU在数学深度教学中的应用
TRU在教学设计、课堂教学评价、教学研究等实践环节中均有其价值。理论上如果课堂教学能按TRU的五个维度设计实施,学生将有可能成为渊博睿智的思考者和学习者。但如果这些教育理论不能以一线数学教师能够接受的方式呈现,其价值就无法体现。因此以一线教师能够实际操作的语言和方式应用TRU的理论具有重要意义。
1.作为改善教学设计的工具
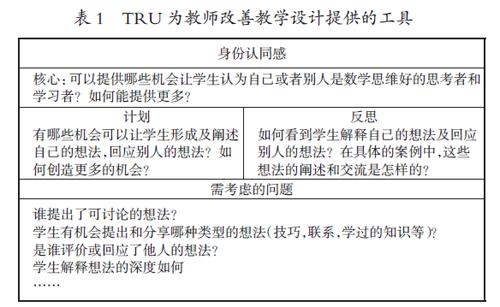
课堂教学随时代发展变化,没有绝对正确的课堂教学方式。TRU框架从备课和反思围绕教学设计提出相应的问题。首先在备课阶段,教师需要依情况选择教学内容,TRU提供了一系列问题,以帮助教师审视对学生认知需求的满足程度,如:为学生获得重要思维提供了哪些机会?如何回应学生的努力并保证学生能发展自己的思维和理解?其次在反思阶段,反思上一阶段的完成度并继续调整。TRU从各维度设计了有助于教师专业发展的工具,下表是身份认同感维度的工具。
2.作为听课评课的工具
课堂观察是教师提高专业素养的重要途径,相关反馈有助于教师认识自身得失,实现深度教学目标。课堂观察的反馈可来自不同角度, TRU针对不同维度设计了课堂观察表。以下为形成性评价的课堂观察表(表2):
为所有学生阐述理解提供了哪些机会?对建立已揭示的思想有哪些机会?教师或学生如何抓住这些机会?哪些方面可以进一步提高?
目标:持续灵活地提供一些技巧和活动,让学生能表达他们新出现的理解,并通过重新思考误解及建立有效的观点加强学生的学习。
从上表可见,形成性评价的课堂观察师生的课堂表现并提供建议。TRU的五个维度彼此联系,观察者可以将其他相关维度的评价列在表中。
综上,TRU描述了有效课堂的属性,提供了研究课堂教学的框架和工具。教师借此计划和反思教学,在教学评价中寻求反馈,将促使数学课堂向深度教学发展,学生在这样的课堂中能够实现更为清晰、深入、全面、合理的思考。
五、结语
TRU研究在追求培养学生数学思维习惯的宗旨下,致力于探究优质的深度教学课堂所具备的基本属性。在多元文化的背景下,数学课堂具有多样性,TRU在现有研究的基础上,以培养学生数学地思维为出发点,体现了数学深度教学的目标。TRU将数学深度课堂的基本要素归结于五个维度,并在某种程度证明了这个框架的完备性。这一思路类似于数学研究中的理性精神,将原本模糊复杂的系统,以结构的角度更清晰地刻画出来,使得深度课堂教学不再是令一线教师无法厘清的概念。
尽管TRU项目是在西方文化的背景下针对西方课堂进行的,但该研究得出的评价工具,是一线教师在改进深度课堂教学中能够理解且容易达到的。历史总是告诫着今人:文化的交融互鉴推动着人类的进步,创造出无限的机遇与希望;拒绝融合与交汇的文明,只能在闭锁的环境中迎来灭亡。作为文化自信的大国,中国历来对外来文化拥有强大的吸收能力与兼收并蓄的胸襟。对于中国的教育研究者来说,源自于西方的TRU用数学的理性和批判性思维去研究数学课堂,也是值得借鉴的方面。用于启迪未来的智慧,如能照亮前路,则不需要顾忌其出处。在世界政治经济全球化,人类共同体逐渐成型,中国蓬勃发展、国力腾飞的今天,与时俱进地引入西方的TRU相关理论,将它与中国国情、教育界的现状相结合,便可在数学乃至全学科的教学领域,擘画出一幅美美与共、恢弘壮丽的全新图卷。
参考文献
[1]郑毓信.以“深度教学”落实数学核心素养[J]. 小学数学教师, 2017,(9): 4-10.
[2] Schoenfeld A H. What Makes for Powerful Classrooms, and How Can We Support Teachers in Creating Them? A Story of Research and Practice, Productively Intertwined[J]. Educational Researcher, 2014, 43(8): 404-412.
[3]周九诗, 鲍建生. 美国”TRU”课堂评价模型介绍及其启示[J]. 外国中小学教育, 2016, (12): 52-56.
[4] Schoenfeld A H. Video analyses for research and professional development: the teaching for robust understanding (TRU) framework[J]. Zdm the International Journal on Mathematics Education, 2018, 50(8): 1-16.
[5]喻平.教师的认识信念系统及其对教学的影响[J]. 教师教育研究, 2007, 19(4): 18-22.
[6] Schoenfeld A H. Thoughts on scale[J]. Zdm the International Journal on Mathematics Education, 2015, 47(1): 161-169.
[7]张良. 深度教学“深”在哪里?——从知识结构走向知识运用[J]. 课程·教材·教法, 2019, 39(7): 34-39.
[8] Boaler J. The Development of Disciplinary Relationships: Knowledge, Practice and Identity in Mathematics Classrooms[J]. For the Learning of Mathematics, 2002, 22(1): 42-47.
[9] Scheerens J. Opportunity to Learn, Curriculum Alignment and Test Preparation[M]. Springer International Publishing, 2017.
[10] Schoenfeld A H. Errata: Making Mathematics Work for All Children: Issues of Standards, Testing, and Equity[J]. Educational Researcher, 2002, 31(3): 37.
[11] Schoenfeld A H. Measures of Problem-Solving Performance and of Problem-Solving Instruction[J]. Mathematical Problem Solving, 1982, 13(1): 31-49.
[12] Black P, Wiliam D. Assessment and Classroom Learning[J]. Assessment in Education Principles Policy & Practice, 1998, 5(1): 7-74.
[13] Black P, Harrison C, Lee C, et al. Working Inside the Black Box: Assessment for Learning in the Classroom[J]. Phi Delta Kappan, 2004, 86(1): 8-21.
[作者:左浩德(1987-),男,江蘇扬州人,扬州大学数学科学学院,讲师,博士;郭婵婵(1988-),陕西延安人,延安大学数学与计算机科学学院,讲师,博士。]
【责任编辑 刘永庆】
