基于静态电压稳定的微电网需求响应研究

曹 佳，曹建国

（1. 株洲中车时代电气股份有限公司，湖南 株洲 412001；2. 中车株洲电机有限公司，湖南 株洲 412001）

0 引言

随着新能源并网渗透率的提高、分布式能源及柔性负荷的引入，对微电网的安全、稳定运行提出了更高的要求并带来了更大的挑战。电压稳定裕度作为系统静态电压稳定的评估指标，能够客观反映系统当前电压状态并给出系统电压最薄弱支路信息，为系统稳定分析提供基础。

目前，评估电网静态电压稳定的方法包括灵敏度指标分析法[1]、最小模特征值指标分析法[2]、雅可比矩阵奇异值分析法[3]及电压稳定局部指标(L指标)分析法[4]等。灵敏度指标分析法[1]以潮流计算为基础，利用系统相关的状态变量或输出变量之间的微分关系研究系统的电压稳定性。最小模特征值指标分析法利用最小模特征值和特征向量分析系统所处的运行状态，从而找出最优的节点位置进行无功补偿[2]。奇异值分解法[3]用潮流方程雅可比矩阵的最小奇异值表示系统当前运行点和电压稳定极限之间的距离。L指标分析法[4]既不需要计算潮流方程雅可比矩阵对应的特征值和奇异值，也不需要计算系统状态变量或输出变量之间的微分关系，具有物理概念清晰、求解速度快的特点，能快速给出每条线路的稳定性指标。

基于微电网电压稳定的课题研究也涉及多个方面：文献[5]建立了一种可实现微电网静态电压稳定、可再生能源消纳最大化等微电网多目标规划的模型，使规划能同时达到静态电压稳定、新能源消纳和经济性能的平衡。为改善含双馈异步风力发电机组微电网的静态电压稳定性，文献[6]提出一种基于就地层储能稳定控制和双馈异步风力发电机组快速变桨控制的静态电压稳定增强控制策略，以保证微电网的安全稳定运行。在采用下垂控制方式的微电网系统中，文献[7]根据雅可比矩阵奇异值分解法求出最小奇异值及其左右奇异向量，并根据最小奇异值对应的右奇异向量之和来较准确地分析微电网电压的稳定性。文献[8]采用分岔理论来分析微电网的静态电压稳定性，连续潮流追踪微电网的平衡解流形曲线，并根据特征根类型识别曲线鞍结分岔点，从而给出系统电压的稳定裕度。文献[9]将特征结构分析法应用于微电网静态电压稳定性问题，利用节点电压参与因子并结合Tellegen 定理求出电压相对灵敏度，从而判断系统薄弱区域以及关键支路。

上述研究大多以配电网或者将某个分布式电源(distributed generation，DG)当成平衡节点处理为背景，主要集中在传统的静态电压稳定机理性研究和工程应用，而基于静态电压稳定的孤岛微电网需求响应研究仍不多见。本文基于孤岛微电网下垂控制潮流计算结果和线路参数得出的每条支路电压稳定局部指标(L指标)，提出一种无功功率需求响应策略，其每条支路具有一定容量的负荷并按照响应策略进行重新分配，最终使系统每条支路L指标尽可能达到均衡、系统电压稳定的效果；并计算、分析了负荷需求响应容量和DG 接入位置对结果的影响。

1 孤岛微电网潮流计算

孤岛微电网与常规电力系统输电网、配电网潮流计算的最大差异在于没有将DG 等效为平衡节点，因此系统电压和频率靠下垂控制方式调节。

1.1 下垂控制DG 装置模型

采用下垂控制策略的孤岛微电网DG 装置通常可等效处理为下垂节点、PQ 节点和PV 节点3 种类型[10]。由于线路等效阻抗主要表现为感性，下垂控制节点通常采用P-f/Q-U控制策略，即

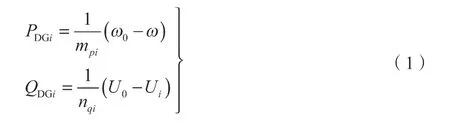
式中：PDGi——第i个下垂控制DG 装置提供给孤岛微电网的有功功率；QDGi——第i个下垂控制DG 装置提供给孤岛微电网的无功功率；ω0——下垂控制DG 装置空载角频率；ω——下垂控制DG 装置系统稳态角频率；U0——第i个下垂控制DG 装置空载输出电压幅值；Ui——第i个下垂控制DG 装置实际输出电压幅值；mpi——下垂控制节点i的有功功率静态下垂增益；nqi——下垂控制节点i的无功功率静态下垂增益。

为保证系统频率和电压幅值安全调节，下垂控制的静态下垂增益由式（2）确定：

式中：PDGi,max，QDGi,max——第i个下垂控制节点提供至微电网的有功功率和无功功率的最大值；UDGi,max，UDGi,min——第i个下垂控制节点最大和最小电压幅值；ωmax，ωmin——系统角频率的最大值和最小值。

1.2 负荷模型

由于孤岛微电网负荷特性跟随负荷端点电压U和系统频率ω变化，采用下垂控制的孤岛微电网的稳态频率未知且一般不等于工频，故静态负荷模型需计及频率和端电压的影响[11]。

式中：f和f0——系统实际频率值和设定频率值；P0i，Q0i——节点i在设定频率下的有功负荷和无功负荷；PLi，QLi——节点i实际有功负荷和无功负荷；α，β——负荷有功、无功功率指数，不同类型负荷的功率指数值不同；kpfi，kqfi——负荷有功功率、无功功率的静态频率特性参数。

1.3 孤岛微电网潮流方程

针对孤岛微电网系统不同类型节点，需要分别列写潮流方程。

PQ 节点潮流方程为

式中：ΔPPQi，ΔQPQi——第i个PQ 节点的有功功率和无功功率的残差量；PGi，QGi——第i个PQ 节点DG 提供的有功功率和无功功率；Gij，Bij——线路i-j的电导和电纳；θij——节点i与j之间相角差。

PV 节点潮流方程为

式中：ΔPPVi——第i个PV 节点的有功功率的残差量。

如果计算出的无功功率超出DG 装置实际输出功率的限值，则需将PV 节点转化为PQ 节点，无功功率保持在限制值。

下垂节点潮流方程为

式中：ΔPDi，ΔQDi——第i个下垂节点有功功率和无功功率的残差量。

综上，可将孤岛微电网不同类型节点对应的潮流方程（即式（4）～式（6））合并为非线性方程组：

其中，x=[ω,θT,UT]T，x∈R2n，θ=[0,θ2, …,θn]T。U=[U1, …,Un]T，设定θ1=0。

采用牛顿-拉夫逊法对潮流方程式（7）进行求解。首先需对潮流方程进行一阶泰勒展开，然后采用牛顿步dk修正原迭代步，并将潮流方程组对应残差量的无穷范数max(||ΔPi||, ||ΔQi||)作为迭代收敛条件：

式中：Jk——潮流方程第k次迭代对应的雅可比矩阵。

2 基于电压稳定L 指标的需求响应策略

根据上述计算的潮流结果，对系统任意一条线路i-j，可以得到

式中：Pi和Qi——线路端节点i处的有功功率和无功功率；Pj和Qj——线路末节点j处的有功功率和无功功率；R和X——线路i-j之间的电阻和电抗。

以Pi和Qi为自变量，近似认为端电压Ui幅值的标幺值为1.0，则式（9）有实数解的条件为[12]

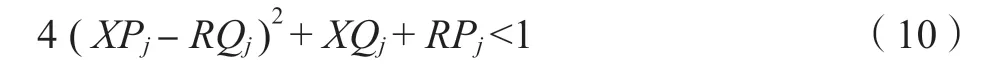
第i条支路的电压稳定指标Li近似值，具体如式（11）所示。Li越小，系统第i条支路电压稳定性越好；反之，则该支路电压稳定性越差；当Li接近于1.0 时，该支路电压崩溃。

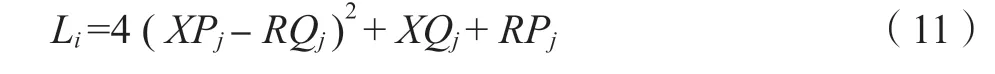
全系统电压稳定指标L取所有支路中的最大电压稳定指标，即可识别每条支路电压稳定情况。

式中：N——系统支路总数目，可根据L值与临界值1.0的距离来判断系统电压稳定的程度。

基于式（11）得到各线路的电压稳定Li值，本文提出一种基于L指标的无功功率需求响应策略。其模型首先假设各条支路参与需求响应的无功负荷容量为当前支路一定比例的无功负荷；然后再将支路负荷无功的变化量均分到支路两端非零负荷节点；最后采用两种方式进行负荷有功功率的调整。方式1，需求响应过程中保持负荷功率因数不变，即节点负荷无功功率确定后，节点负荷有功功率也随之确定。方式2，需求响应过程中负荷功率因数可以改变，即节点负荷无功功率确定后，节点负荷有功功率仍按式（3）计算得到。两种方式均既能保证负荷的调节裕量，又能保证系统运行的安全性。具体的需求响应模型如下：

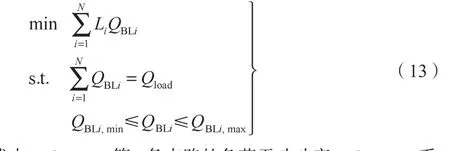
式中：QBLi——第i条支路的负荷无功功率；Qload——系统所有支路负荷无功功率总和；QBLi,max，QBLi,min——第i条支路负荷无功功率的上、下限值。

根据上述模型得到需求响应完成后的各支路负荷无功功率。首先，将各支路响应前后的变化量均分到相应非零负荷节点，并采用上述所提2 种方式分别进行节点负荷有功功率的调整。然后，进行需求响应后的潮流计算，以检验各节点电压水平和各支路Li指标情况。若出现节点电压越限或某条支路Li指标接近1，则需要对负荷进行局部调整。

3 算例分析

为探究基于静态电压稳定的微电网需求响应策略对微电网电压稳定及潮流分布的影响，本文重点研究无功负荷需求响应容量和分布式电源DG 接入位置对结果影响的程度。

3.1 需求响应为负荷容量的±10%

本文将基于静态电压稳定的微电网需求响应模型应用于改进的37 节点孤岛微电网测试系统中(图1)[10]。该测试系统在IEEE-33 节点系统的基础上，分别在第18，22，25 和33 节点接入4 个DG 装置，从而构成37 节点孤岛微电网系统，即新支路为18-34，22-35，25-36，33-37。其中，支路序号1 指节点1 与节点2 之间的支路，支路序号2 指节点2 与节点3 之间的支路，然后依次往后延伸形成新的支路序号，系统共有36 条支路。计算环境如下：1.99 GHz CPU，16.00 GB RAM，MatlabR2015a。所有数据均以标幺值给出，系统基准频率为50 Hz，基准容量为1 MW，基准电压为12.66 kV，系统频率安全运行范围为0.996～1.004 p.u.，电压安全运行范围0.94～1.06 p.u.。4 个DG 装置均采用P-f/Q-U下垂控制，1 节点电压相角设定为0，4 个DG 与连接点之间的线路阻抗标幺值均为R+jX= 0.012 453+j0.012 453，ω0=1.004 p.u.，U0=1.06 p.u.。DG 装置和负荷的相关参数见参考文献[10-11]。

图1 37 节点孤岛微电网结构图Fig. 1 Structure of the 37-bus islanded micro-grid

假设各条支路参与需求响应的无功负荷容量为各支路当前无功负荷的±10%，节点注入功率，负荷总功率和线路损耗的仿真计算结果如表1、表2，其中“需求响应后1”表示不改变节点负荷功率因数参与需求响应，“需求响应后2”表示可改变节点负荷功率因数参与需求响应。

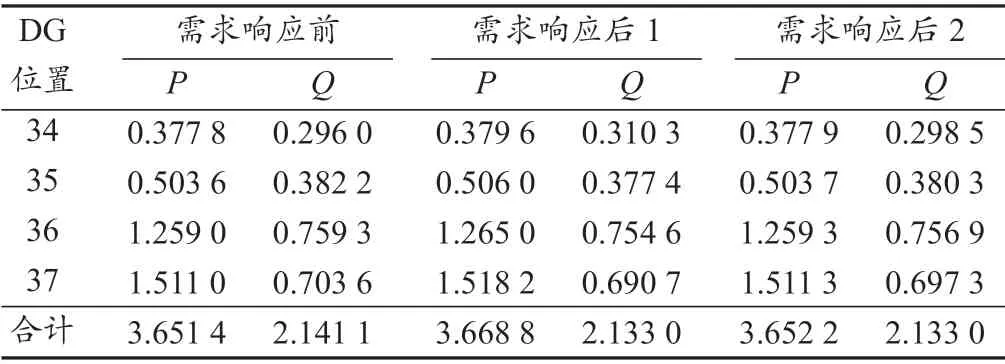
表1 DG 装置节点注入功率Tab. 1 Injected powers of DG units

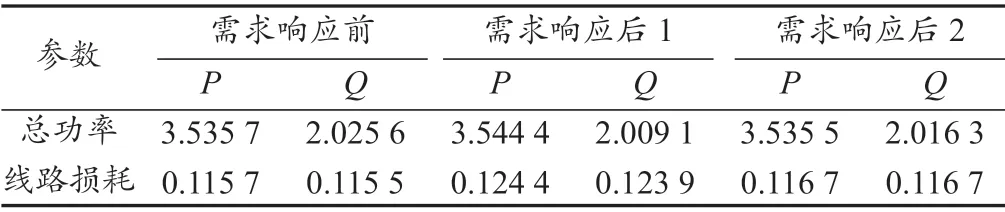
表2 负荷总功率和线路损耗Tab. 2 Total power of load and line loss

从表1 和表2 可以看出，各支路无功负荷参与两种方式下的需求响应后，DG 提供的总无功功率均从2.141 1 p.u.降低至2.133 0 p.u.，节点负荷总无功功率从2.025 6 p.u.分别降低至2.009 1 p.u.（方式1）及2.016 3 p.u.（方式2），但线路无功总损耗从0.115 5 p.u.分别上升至0.123 9 p.u.（方式1）及0.116 7 p.u.（方式2），说明支路无功负荷参与需求响应后改变系统稳态潮流分布，以增大线路网损为代价减小DG 的无功功率。并且，方式2 较方式1，由于其负荷功率因数不固定且负荷有功功率减少0.008 9 p.u.，故采用方式2 时，系统传输有功功率的减小将进一步促使其无功功率损耗一定量的减小。

图2～图8示出各支路参与响应前后参数变化情况。计算得到响应前后的角频率分别为0.995 0（需求响应前）、0.994 9（需求响应后1）、0.995 0（需求响应后2）。图2 示出需求响应前后支路L指标。可以看出，需求响应前支路L指标最大值0.028 0，距离“L=1”电压临界稳定状态还有一定空间，故可认为该微电网系统处于电压稳定状态。对比需求响应前后计算结果，发现各支路负荷具有从高L指标到低L指标转移的趋势，保证系统电压稳定，但受负荷需求响应容量的限制，各支路L指标变化不显著。

图2 需求响应前后支路L 指标Fig. 2 L indices of branches before and after demand response

图3～图6 分别示出需求响应前后支路无功功率、支路有功功率、节点负荷无功功率和节点负荷有功功率。可以发现，节点32 和33 的负荷无功功率变化较大，这是因为支路负荷参与需求响应被分摊到相应负荷节点，导致节点33 的负荷越限。一方面，由于与节点33 相邻的节点37 为DG 接入节点，且DG 接入节点均不带负荷，故只能将节点33 负荷的功率分摊到相邻的节点32，并将节点33 的负荷无功功率设置为微小量（0.000 1 p.u.）。另一方面，方式1 维持节点负荷功率因数不变，则节点有功负荷将跟随节点无功负荷而变化；方式2 负荷功率因数不固定，其支路有功负荷而变化与方式1 存在差异，而节点有功负荷变化与方式1 的差异不显著。

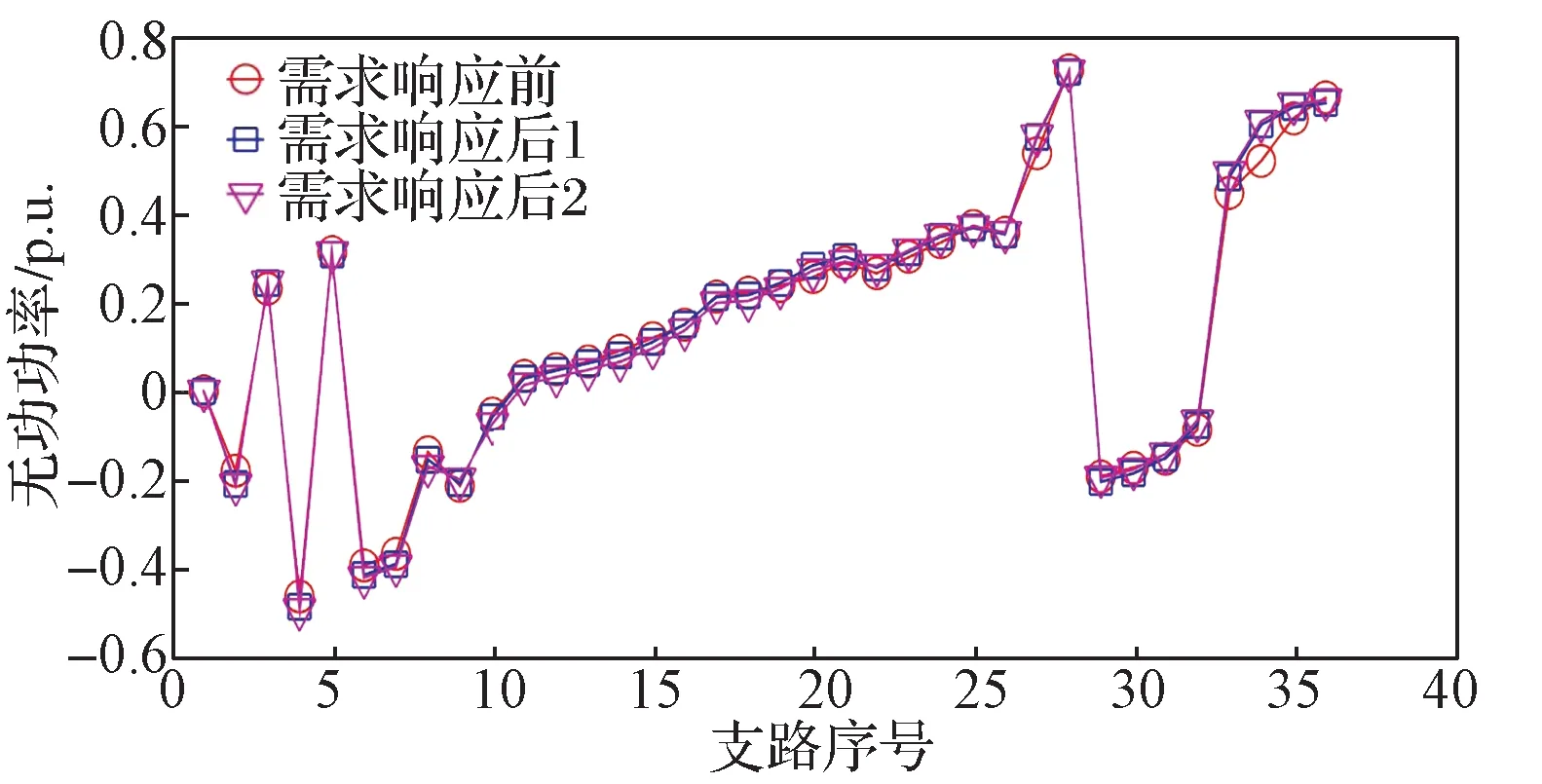
图3 需求响应前后支路无功功率Fig. 3 Reactive powers of branches before and after demand response

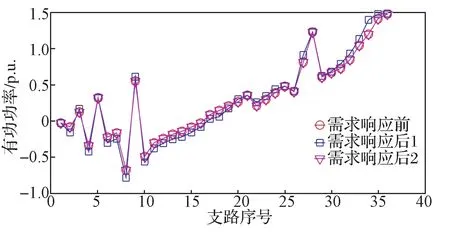
图4 需求响应前后支路有功功率Fig. 4 Real powers of branches before and after demand response

图5 需求响应前后节点负荷无功功率Fig. 5 Reactive powers of loads before and after demand response

图6 需求响应前后节点负荷有功功率Fig. 6 Real powers of loads before and after demand response

图7 和图8 示出需求响应前后系统节点电压幅值和相角的变化情况。可以看出，由于支路负荷参与需求响应，改变了系统原有潮流分布；但各节点电压幅值均在从0.94 p.u.到1.06 p.u.的安全范围内，且系统最大相角差也未超过90°，进一步说明该系统处于电压稳定状态。

图7 需求响应前后节点电压幅值Fig. 7 Amplitudes of node voltages before and after demand response

图8 需求响应前后节点电压相角Fig. 8 Phase angles of node voltages before and after demand response

3.2 分布式电源DG 接在不同的位置

在3.1 节的基础上，改变DG 接入位置，并分析位置改变对需求响应结果的影响，即将3.1 节中DG 接入位置修改为节点4, 9, 18, 27，新支路修改为4-34, 9-35, 18-36, 27-37，如图9 所示，其余工况与相关参数均与3.1节一致。同样，假设各条支路参与需求响应的无功负荷容量为各支路当前无功负荷的±10%，并分别计算两种不同功率因数方式下的潮流分布。计算得到响应前后的角频率分别为0.995 0（需求响应前）、0.995 1（需求响应后1）、0.995 0（需求响应后2）。

图9 37 节点孤岛微电网结构Fig. 9 Structure of the 37-bus islanded micro-grid

表3 和表4 分别示出DG 装置节点注入功率以及负荷总功率和线路损耗。可以看出，需求响应前后，系统总无功负荷从1.908 7 p.u.分别降至1.904 7 p.u.（方式1）、1.908 1（方式2），但系统DG总无功功率由2.065 0 p.u.分别变为2.062 2 p.u.（方式1）和上升至2.066 8 p.u.（方式2）。两种不同方式下的线路无功损耗分别从0.156 3 p.u.上升至0.157 5 p.u.（方式1）和0.158 7（方式2）。同时，方式1 下系统负荷总有功功率及DG 总有功功率均小于方式2。相对3.1 节结果，改变DG 接入位置，增大系统线路总损耗，但明显降低DG 功率和负荷总功率，说明DG 接入位置对微电网负荷分布、线路损耗的影响不能被忽略。

表3 DG 装置节点注入功率Tab. 3 Injected powers of DG units

表4 负荷总功率和线路损耗Tab. 4 Total power of load and line loss

图10～图14 分别示出需求响应前后支路的L指标、无功功率、有功功率及节点负荷的无功功率和有功功率。可以看出，除支路7, 14, 23, 31 外，其余支路L指标均分布于“0”值附近，且负荷同样具有从高L指标向低L指标转移的趋势。对比3.1 节，发现需求响应前支路最大L指标为0.031 6，大于3.1 节中的最大L指标，说明DG 位置的改变会影响系统电压的稳定性。由于支路无功功率参与需求响应，使相应节点负荷进行二次调整，但节点3，9，15，27 号的无功负荷超出调节范围，只能将这部分负荷分摊到相邻节点。相较3.1 节，方式1需求响应后节点负荷变化幅度较大，特别是节点负荷有功功率波动较需求响应前有显著差异；而方式2 的节点负荷功率因数不维持恒定，使需求响应后的节点负荷波动范围小于方式1 的。

图10 需求响应前后支路L 指标Fig. 10 L indices of branches before and after demand response

图11 需求响应前后支路无功功率Fig. 11 Reactive powers of branches before and after demand response

图12 需求响应前后支路有功功率Fig. 12 Real powers of branches before and after demand response

图13 需求响应前后节点负荷无功功率Fig. 13 Reactive powers of loads before and after demand response

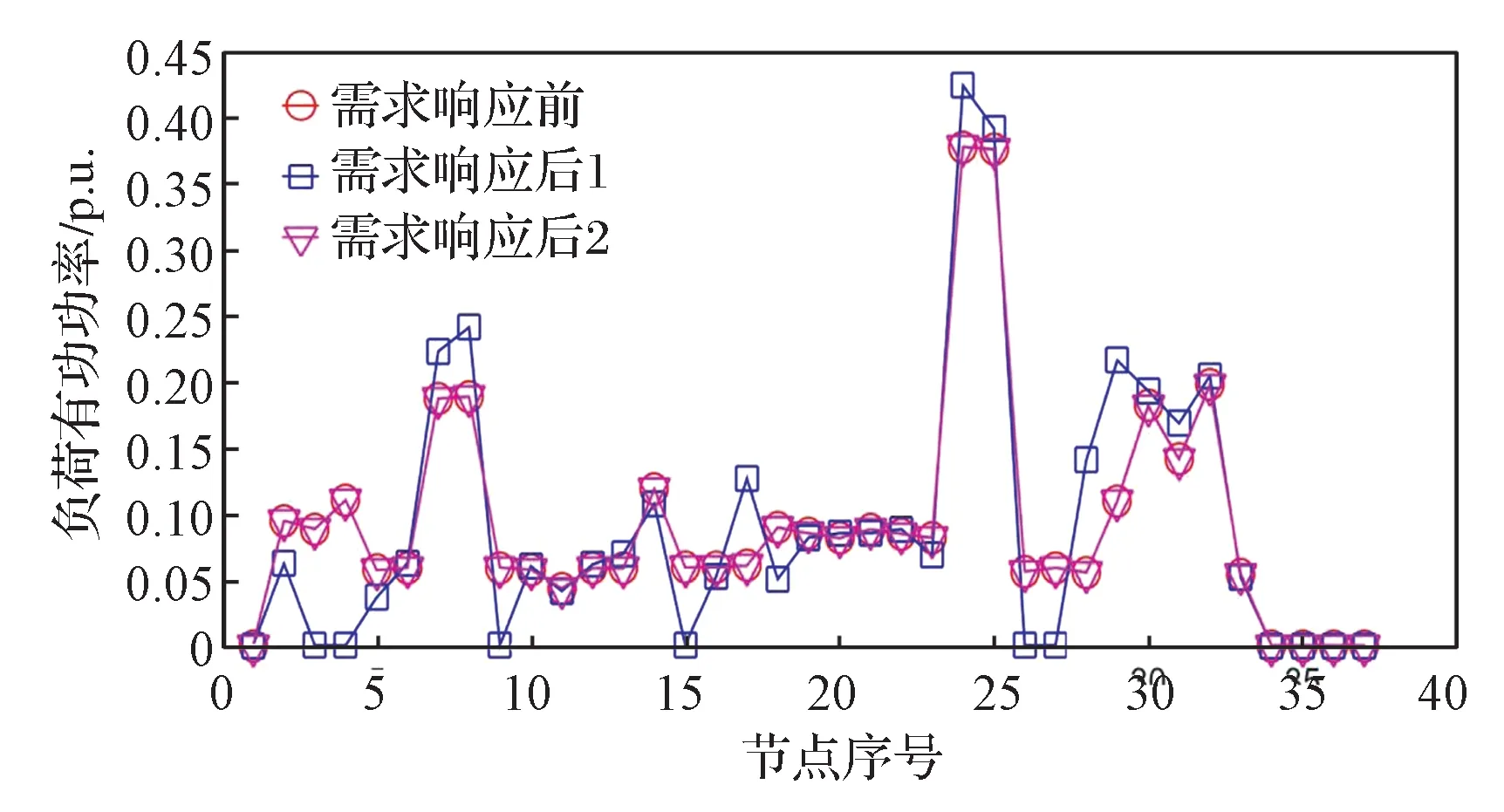
图14 需求响应前后节点负荷有功功率Fig. 14 Real powers of loads before and after demand response

图15 和图16 分别示出需求响应前后节点电压幅值和节点电压相角。可以看出，需求响应之前的部分节点电压幅值已超出安全运行范围(0.94 p.u.～1.06 p.u.)，如节点20～25、节点31～33，节点电压最小值为0.930 5 p.u.，进一步说明改变DG 位置会对系统电压的稳定性带来一定的影响；但节点电压相角差的最大值远未超过90°，说明此时系统仍然稳定。需求响应后，大部分电压幅值越限的节点均朝着安全运行范围变化，仅少部分节点电压幅值略低于响应前的节点电压幅值，这是受需求响应容量限制、节点负荷分摊原则约束所导致。因此，为进一步提升低电压节点的幅值，保证系统电压安全稳定，可考虑在相应节点加装并联电容器或者无功补偿器。

图15 需求响应前后节点电压幅值Fig. 15 Amplitudes of node voltages before and after demand response

图16 需求响应前后节点电压相角Fig. 16 Phase angles of node voltages before and after demand response

4 结语

本文主要研究孤岛微电网静态电压稳定的需求响应问题，DG 均采用统一的下垂控制方式，给出一种无功负荷基于L指标的需求响应模型，并从负荷需求响应容量、DG 接入位置两方面进行计算与分析。计算结果表明，基于电压稳定L指标的负荷需求响应对系统电压稳定具有一定的积极作用，影响程度主要受负荷需求响应容量、节点负荷分摊原则等约束；DG 接入不同位置改变系统及潮流分布，对系统电压稳定性的影响不能忽略。

为全面评估DG 的不同控制方式、不同的需求响应策略模型，下一步将研究静态及暂态环境下不同电压稳定指标对系统电压稳定的影响。