基于预测控制的货运机车自动驾驶技术研究
2020-02-22张征方沈子扬
李 程,张征方,沈子扬
(中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
货运机车属于强非线性、大惯性系统,在运行时会受到外部干扰(如:坡度、空气阻力和线路湿滑等)、内部参数变化(因负载和环境温度等因素变化而造成)等因素的影响。与客运列车相比,货运列车具有载重大、每趟次载重差异明显、货物类型多样、起车和停车类型复杂等特点,操作约束(如速度限制、操作限制、级位保持等)更为复杂。传统的控制策略存在超调难以被抑制、对时滞性和非线性的适应性差等问题,难以在满足线性约束的情况下实现列车的多目标优化(平稳、节能)控制[1],因此迫切需要一种能适应货运列车运行模式的自动驾驶系统。
随着车载和地面安全信号系统、机车车辆智能控制等技术的发展,货运自动驾驶技术的研究对于提高运输效率、货运列车准点率和安全管理水平以及降低运用成本,具有重要的研究价值和应用意义[2]。目前在轨道交通货运列车自动驾驶领域,国外只有澳大利亚对其进行了应用研究和实验[3-4],但始终未能达到设计要求;而国内对此尚无运营实例报道。随着自动驾驶技术的发展,对控制算法的研究也取得了一定的成果。传统的速度跟踪控制算法,如最优控制和PID 控制,都具有各自的不足。最优控制需要在具有控制对象全部先验知识的前提下对模型进行全局的优化,如果控制对象发生变化或模型有偏差,系统优化性能会变差甚至系统不稳定。PID控制属于反馈控制,其仅通过反馈信息进行跟踪,没有模型预测和性能优化功能。预测控制弥补了上述两种控制算法存在的不足,一方面基于一定控制对象先验知识,对控制模型进行优化;另一方面,为了解决实际控制中存在的扰动和误差问题,引入反馈机制进行滚动优化和反馈校正[5],并通过连续局部最优化和反馈校正方法的结合保证了对控制对象的有效控制。
本文基于已有的研究成果,提出了一种基于T-S模糊策略的模型预测控制(model predictive control, MPC)改进算法。其利用基于状态空间方程的模型预测控制,在满足控制约束的情况下实现多目标优化[6-9];同时,基于T-S 模糊模型构造列车多模型切换控制策略,从而减少由于强非线性带来的系列控制问题。最后,在西康线的货运机车半实物仿真平台上给出了本控制算法的仿真结果。
1 机车运行模型的建立
1.1 机车模型组成
自动驾驶系统通过接收LKJ 装置数据(包含列车线路信息、车辆信息及安全信息等)、车载控制系统及列尾装置的数据,基于自动驾驶控制策略实现对机车牵引系统和制动系统的控制,最终实现机车的自动驾驶功能[10-12]。机车自动控制系统结构模型组成如图1 所示。可以看出,在自动驾驶系统中,ATO 控制器根据参考速度曲线自动生成牵引、制动等控制指令并传输给机车牵引和制动控制系统。
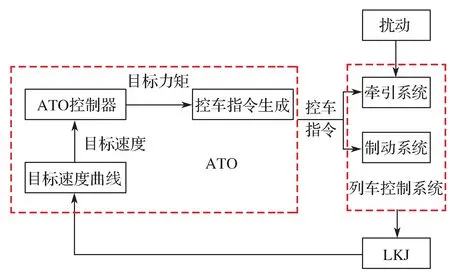
图1 机车自动控制系统结构框图Fig. 1 Structure diagram of train automatic control system
1.2 机车动力学模型的状态方程建立
在机车牵引计算中,通常采用单质点模型,即把整列车看成一个没有尺寸和大小的质点,其所受的力都作用在一个点上,这种方法的优势在于牵引计算容易实现。由于实际线路纵断面不同,为了更加精确地进行受力分析,牵引计算时采用平均坡道阻力和平均弯道阻力。单质点列车模型如图2 所示,其中M为列车总质量,g为重力加速度,Ft为牵引/制动力,Fr为列车运行阻力(其包括基本阻力、平均坡道阻力和平均弯道阻力),FN为支持力,由此求得列车运动方程:

式中:am——由Ft求得的目标加速度。
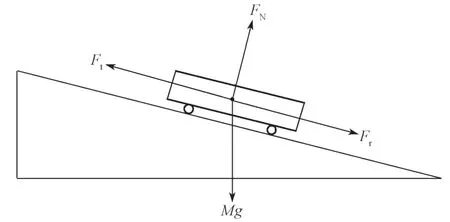
图2 单质点列车动力学模型Fig. 2 Single particle train dynamic model
受惯性的影响,列车实际响应的速度难以被迅速跟随;又由于列车网络控制系统存在一定的延时,因此实际加速度相对于目标加速度有一个响应时延τ。综上分析,可采用一个一阶带延时的惯性系统来近似表示列车牵引和制动的过程。

式中:T——响应时间常数;Fact——实际发挥力;Fdes——目标输出力;k——稳态增益;t——当前时刻。
将式(2)两边同时除以M,使动力学关系转化为传递函数的形式,其输入为目标加速度ac,输出为响应加速度,则列车模型传递函数形式如下:
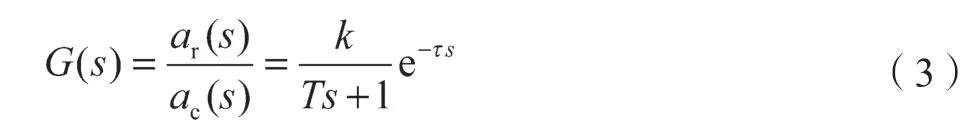
列车的目标加速度ac由速度规划曲线给出的目标速度vref与当前速度v计算得到,列车的实际加速度a(t)由响应加速度ar(t)和阻力加速度ad(t)组成:

列车的速度和加速度之间满足

则由式(4)和式(5)可得

由式(2)可得

根据式(6)和式(7),可以得到如下状态空间方程:
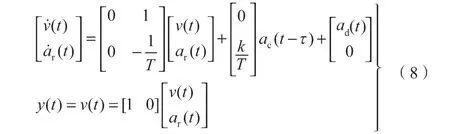
式中:y(t)——速度输出变量。
设采样时间为Ts,将式(8)离散化,得到线性离散系统的状态空间模型:


2 模型预测控制器设计与仿真
2.1 模型预测控制器设计
系统的控制目标是速度跟踪精度。为了避免过大的冲击度(加速度变化),惩罚函数可被定义为[13]

式中:Np——预测步长;Nc——控制步长;Q和R——权重矩阵,其均为对角矩阵;v(k+i)——(k+i)时刻的目标速度;(k+i|k)——根据采样时刻来预测(k+i)时刻的值。
系统的约束涉及加速度与机车牵引/制动力约束、加速度变化率与机车动力约束、速度与防止超速和欠速约束:
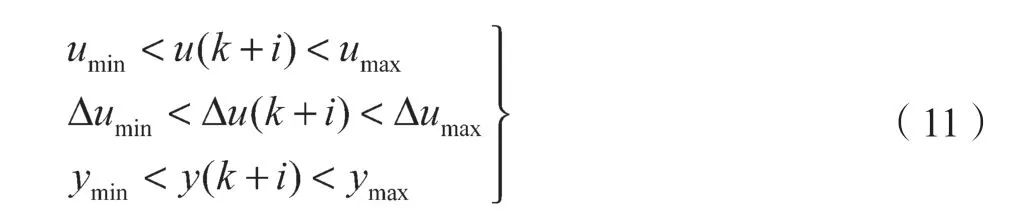
式中:umin,umax——加速度限值,与机车最大牵引力和最大制动力相关;Δumin, Δumax——加速度变化量的限值,与机车牵引/制动力和列车总重等相关;ymin,ymax——运行速度限值,与ATP 高限速和特殊场景下低限速等相关。
MPC 的基本原理是在满足式(11)的前提下使惩罚函数最小。为了消除稳态误差ΔD(k),将状态方程改写成增量形式:

定义矩阵Y=[y(k+1)|ky(k+2)|k…y(k+Np)|k]T, ΔU=[Δu(k-n) Δu(k-n+1) …Δu(k-n+Nc-1)]T,可将式(12)转化为

式中:Sx——速度变化系数矩阵;Su——输入加速度变化系数矩阵;Sd——阻力变化系数矩阵;Iy——单位矩阵。
式(10)可被改写为
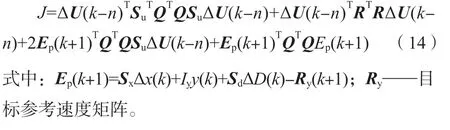
式(14)最后一项与输入无关,故可将惩罚函数转化为标准二次规划问题:
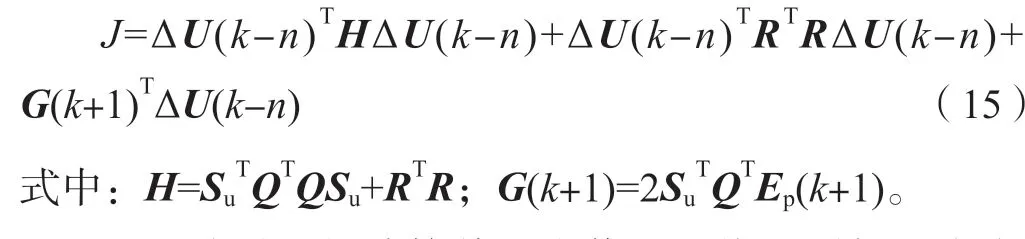
通过式(15)计算其最小值,最终得到加速度变化量Δu,并通过u(k+1)=u(k)+Δu优化式(12)和式(13)中控制输入,同时引入反馈校正,即利用由车载传感器获得的实际速度和加速度来优化参数模型和补偿误差[14-15]。
2.2 仿真测试
综上,针对列车在单一坡道和起伏坡道两种工况,采用传统控制算法和MPC 算法分别进行列车运行控制及对比分析。本文所用列车运行仿真系统为半实物仿真系统,由自动驾驶装置(ATO)、人机交互单元(DMI)、列车运行控制记录装置(LKJ2000)、制动系统(BCU)及网络控制系统(CCU)组成。在实际运行中,根据前方路况信息及车辆状态信息进行探测和规划,得到未来一段距离的速度和工况曲线,并联合网络控制系统、制动系统等单元进行控制指令的输出,从而达到实时控制的目的。
2.2.1 单一坡道工况下
图3 示出在坡道不变的大下坡路段传统控制算法(PID)的控制精度与MPC 控制效果的对比。可以看出,采用传统的控制算法,机车始终没有以一个适当的电制动力进行控制,导致速度曲线呈现周期性振荡,速度跟踪的精度偏差较大;而采用MPC控制,速度曲线能快速收敛,因为在计算电制动力时,MPC 考虑了未来的速度和运行阻力,能够提前对电制动力做出调整,并经过短暂的反馈调节后,对速度进行精准控制,使得实际速度跟随目标速度精度更高。
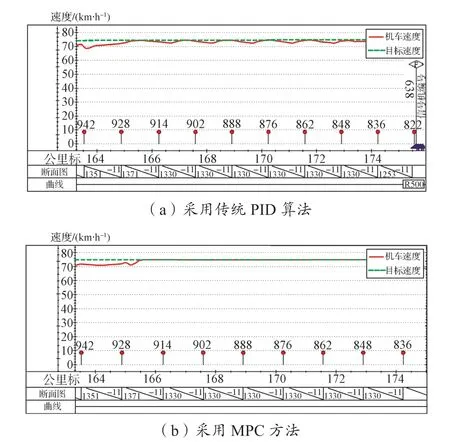
图3 针对单一坡道采用传统算法控制和采用MPC 控制的效果比较Fig. 3 Control results comparison between the systems with traditional control and with MPC in the condition of single slope
实际运行时,由于存在扰动、测量误差等因素,在单一坡道上MPC 施加的力也处于不断变化之中。图4 示出在单一坡道上,传统MPC 为了精准跟随目标速度曲线而施加周期性电制力的情况(红色曲线)。列车是一个大惯性的控制对象,频繁地调节牵引/电制动力,可能会引起系统周期性振荡;同时在传统的手动操纵上,为防止因车钩间隙而引起的列车纵向冲动,也需要避免在单一坡道频繁地调节输出力。可以看出,传统MPC 控制方式并未很好地解决此类问题。
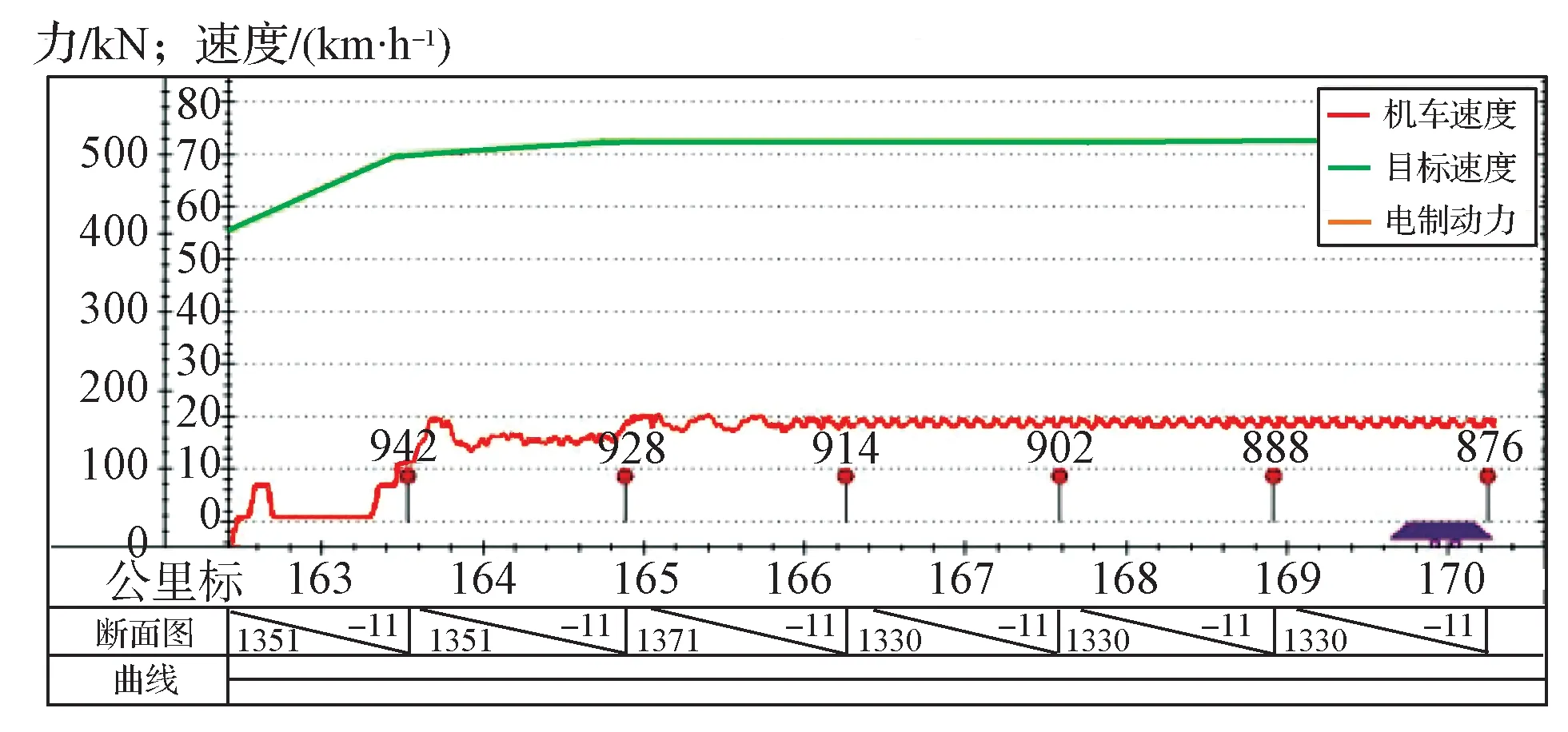
图4 传统MPC 控制效果Fig. 4 Control result of the system with traditional MPC method
综上,需要在目标速度曲线附近增加一个滞环,即在速度和加速度都符合要求时,维持原有输出力不变。另外,在MPC 计算输出力的基础上需要增加滤波,以进一步平滑输出力波形,为此,本文选用中值滤波法。中值滤波法是一种非线性平滑技术,在选取适当的序列长度后,它不受序列的极大值和极小值影响。图5 示出为增加滞环和中值滤波后的控制效果,可以看出,虽然其跟随效果不及传统MPC 控制的,但在较短时间调节后,可以输出一个恒力,使得列车速度也能很好地跟随目标速度曲线,更加符合实际需求。
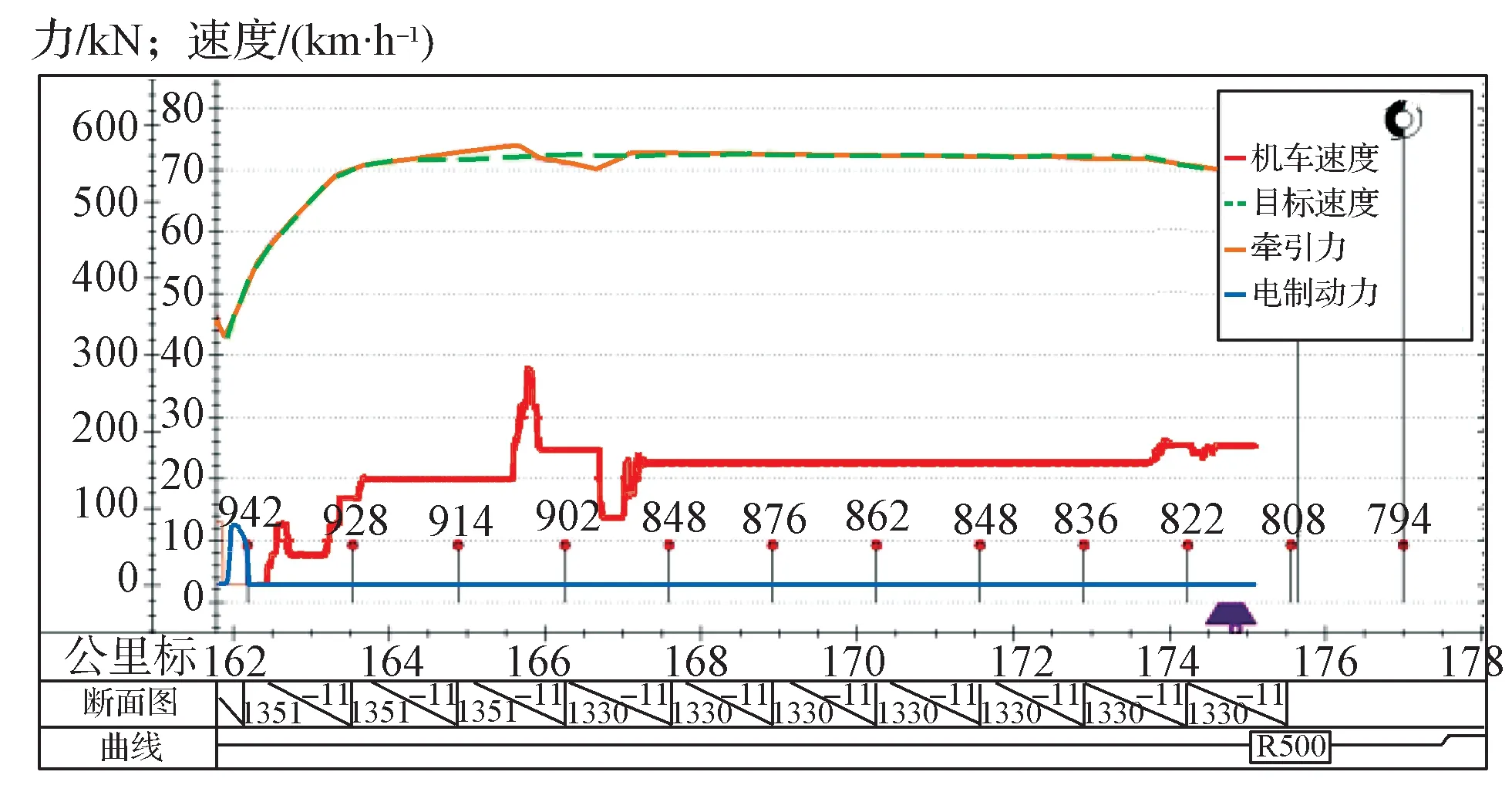
图5 MPC 改进后控制效果Fig. 5 Control result of the system with the improved MPC method
2.2.2 起伏坡道工况下
列车在起伏坡道运行时,若要使车辆速度保持为恒速,不可避免会进行工况转换。由于列车车钩之间存在间隙,有可能会产生较大的冲动,严重影响列车的平稳性。图6(a)和图6(b)为在起伏坡道路段采用传统PID控制算法与采用MPC 方法的控制精度对比。可以看出,采用传统的控制算法,机车牵引力一直处于不断调节状态中,MPC 控制器也处于不断调节中,两者情况基本相同 ;而采用MPC 方法进行控制时,速度跟随精度更高,提高了列车区间运行时间的准确性。

图6 针对起伏坡道采用传统算法控制和采用PMC 控制的效果比较Fig. 6 Control results comparison between the systems with traditional control and with MPC in the condition of undulating slope
2.2.3 复杂坡道工况下
图7 示出一段实际线路中采用MPC 控制器实现跟踪给定速度的效果,其坡道包含有连续上坡道和起伏坡道。可以看出,在这种复杂的坡道组合中,采用MPC方法可以非常精准地控制列车的给定速度,这是因为一方面MPC 在对未来一段时间内的速度和坡道进行模型预测的基础上对输入控制量进行了优化并只用于下一时刻;另一方面,为了解决实际控制中存在的扰动和误差问题,系统引入反馈机制进行滚动优化和反馈校正,通过不断地滚动优化计算局部最优解来近似替代全局最优解,从而保证对控制对象的有效控制。

图7 复杂坡道变化下MPC 控制效果Fig. 7 MPC result of the system in the condition of complicated slope
3 基于模糊模型预测控制器设计
对所采集的货运列车实际运行数据进行分析发现,机车系统具有复杂的非线性特性,不同运行工况下的列车动力学模型参数有所区别,如图8 所示。如果采用同一种模型进行计算,将会造成很大的误差,甚至会因此导致驾驶系统的不稳定,因此需要针对不同的工况进行模型转换。

图8 列车动力学模型转换示意Fig. 8 Schematic diagram of locomotive dynamic model-transformation
3.1 机车系统的非线性模型
根据实际情况,在列车运行过程中,牵引工况和电制动工况彼此独立,不可能同时出现,即:在牵引工况下,系统只能控制牵引力输出的大小,电制动力为零;在电制动工况下,系统只能控制电制动力的大小,牵引力为零。根据上述特征,本文采用了基于阈值的切换策略,即在无输入工况(惰行工况)下,基于不同坡道和不同初始速度,在相同时间内标定列车最大加速度,在此期间车辆只受各种外部阻力的影响。通过半实物仿真平台收集测试数据,可以绘制出不同行驶速度下车辆能获得的最大加速度曲线(图9)。

图9 最大加速度曲线图Fig. 9 Maximum acceleration curve
频繁的牵引/电制动转换一方面不仅不利于列车节能,还会引起车辆冲动,严重影响乘坐的舒适性,更有甚者,一旦施加的冲动力大于车钩所能承受的力,可能存在断钩的风险(这是一种十分严重的事故);另一方面,这种行为也不符合机务段的操作规范。考虑到以上因素,本文在最大加速度曲线的上侧和下侧设置了0.001 m/s²的惰行区间用于缓冲[5-6],即在缓冲区之上采用牵引操作,在缓冲区之下采用电制动操作(图10)。
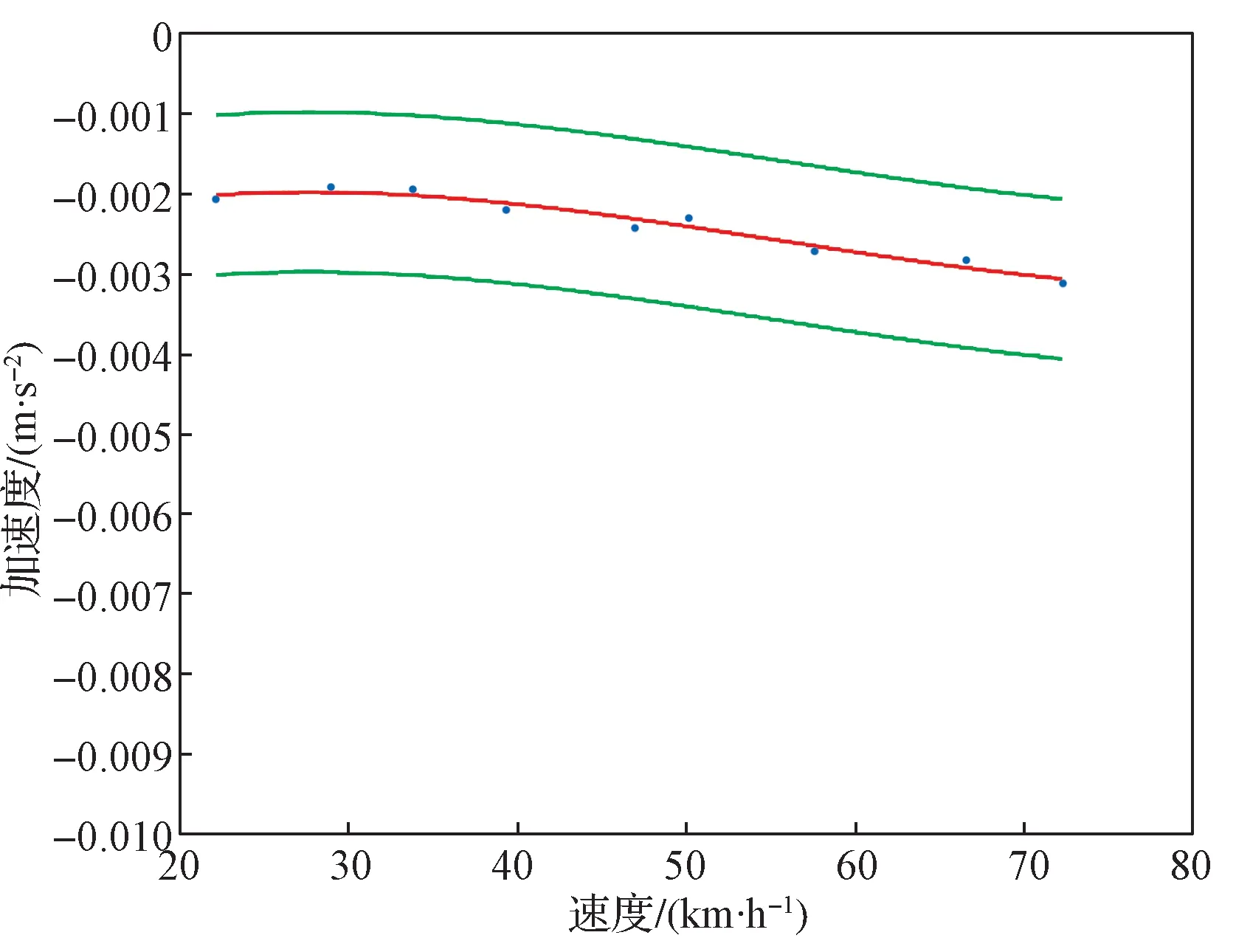
图10 工况切换逻辑曲线Fig. 10 Operational conditions transformation curve
由于状态方程在列车动力学模型的转化点存在较强的非线性,如果在这些点被直接切入到另一个模型,会严重影响控制效果,因此本文引入模糊模型进行工况切换操作。模糊模型是一种非线性模型,它能够解决非线性复杂控制系统的控制,其中T-S 模糊模型是一种常用的模糊控制模型,它通过局部线性化来解决全局非线性化的问题。文献[16-17]已经证明T-S 模糊模型可以将任何平滑的非线性系统逼近至紧致集内的任何精度。因此,为解决列车非线性模型的控制,本文采用T-S 模糊模型将一些线性模型结合起来,通过非线性隶属函数形成整体单一模型。
3.2 基于模糊模型预测控制器设计
在本文中,根据T-S 模糊模型,选择与目标速度曲线的速度偏差作为前提变量,将列车模型用以下的模糊规则描述:

3.3 仿真测试
基于以上分析,利用西安局西康线上行小河镇站与大岭铺站间实际线路数据,采用T-S 模型在匀速和加速两种模型间进行切换,其Matlab 仿真结果如图11 所示。
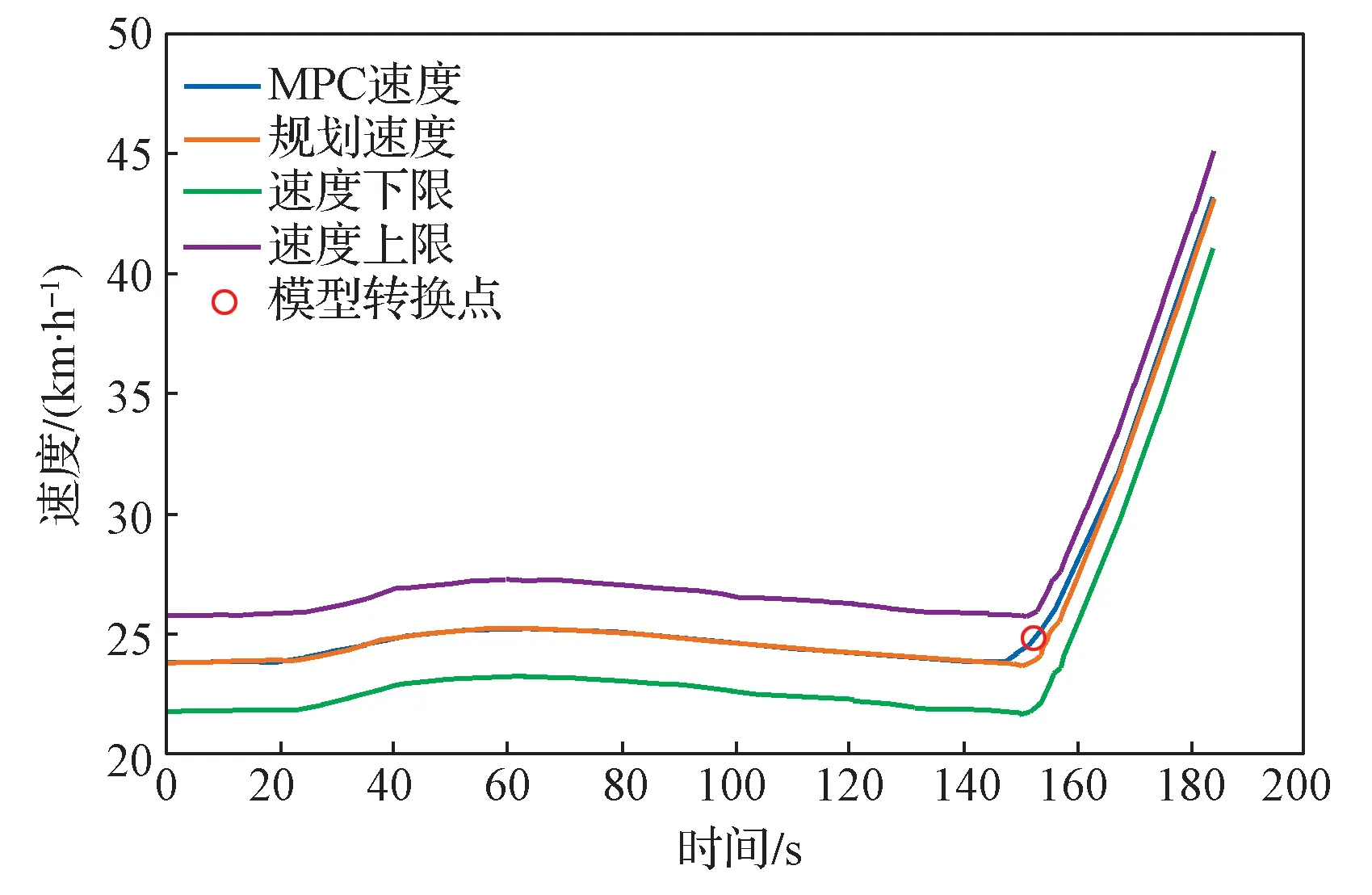
图11 模型转换仿真Fig. 11 Simulation of model-transformation
图12 示出加速模型和匀速模型采用硬切换的列车运行仿真。图13 示出了其采用软切换策略的列车运行仿真。通过对比可以发现,采用硬切换策略时,在每一个采样点采用与当前最为匹配的模型进行控制,在工况变换点时,模型发生了频繁切换,导致控制器参数发生波动,使得控制不收敛;采用软切换策略时,由于加权法可以将两个模型按照一定的线性关系结合起来,利用两个模型不同参数指标,在重合处能够准确地描述实际列车特性。因此,采用软切换的方法更能满足设计需求。

图12 模型硬转换仿真Fig. 12 Simulation of model hard transformation

图13 模型软转换仿真Fig. 13 Simulation of model soft transformation
4 结语
货运机车操纵难度大、模型复杂,传统控制模型无法满足强非线性、大惯性系统的控制要求。为此,本文提出一种基于T-S 模型的改进MPC 方法,以实现对列车速度的精准控制。与传统MPC 方法相比,该方法具有跟踪精度高、输出力稳定且调节平滑的优势。列车运行半实物仿真结果表明,与传统控制方法相比,该方法能够满足实际用户的操纵要求,在一般场景下运行效果较好,也为进一步提高货运机车自动驾驶控制精度提供了一些思路。
由于本文所提方法未考虑过分相、贯通试验等工况;另外,以速度精度和加速度变化量作为控制目标可能在某些运行场景下不符合操纵规范,下一步还需进行多目标优化研究以及实车验证,以进一步提高自动驾驶的控制精度。
