激光摄像式传感器标定方法研究

刘世望，胡云卿，林 军

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

激光摄像式传感器标定是实现轨道交通视觉检测的重要前提之一。利用激光摄像技术进行视觉检测时，图像坐标系与世界坐标系间存在多个自由度的变换，且摄像机镜头存在非线性畸变，所以在视觉检测中对激光摄像式传感器进行高精度标定的难点在于对激光图像进行多自由度的坐标转换及镜头畸变补偿。

激光摄像式传感器标定常见的方法有拉丝标定法[1-2]、锯齿靶标标定法[3-4]和二次交比不变标定法[5-8]，这些标定方法主要存在以下问题：（1）结构光平面的特征点提取困难；（2）结构光平面特征点数量有限；（3） 计算步骤复杂。为解决这些方法的不足，本文采用一种基于针形靶标的运动标定方法，其将结构光平面投射在针形靶标上，形成近似圆形的光斑，其中心即为标定所需提取的特征点；同时针形靶标沿位移平台按固定方向等间隔移动，以获取多组光斑特征点。该方法解决了结构光平面的特征点提取困难和标定特征点数量不足的问题。

文献[9-14]针对视觉检测实际应用，忽略镜头畸变因素，采用摄像机线性模型进行标定，但没有考虑激光摄像式传感器的非线性畸变；文献[15]侧重于将激光摄像式传感器应用于图像特征点提取；文献[16]考虑镜头畸变，建立了非线性标定模型，采用最小二乘法和高斯-牛顿迭代法进行参数求解，但未给出详细的推导过程。

针对上述现状，本文综合考虑激光摄像式传感器镜头径向、偏心及薄棱畸变问题[17-19]，采用基于针形靶标的运动标定方法，建立激光摄像式传感器非线性标定模型；针对模型中待求参数难求解的问题，采用极大似然估计法来降低图像噪声引起的误差，然后用Levenberg-Marquardt（简称“L-M”）算法求出标定参数最优解，并与非线性最小二乘法、高斯-牛顿迭代法进行对比，从而得到高精度的激光摄像式传感器标定方法。

1 激光摄像式传感器标定模型

激光摄像式传感器成像及标定模型如图1 所示。以激光平面作为参考面，建立激光摄像式传感器的世界坐标系OW-XWYW。OW-XWYW平面与激光平面共面，OC-XCYCZC为摄像机坐标系，O-uv为以图像中心为原点的图像坐标系，同时以图像平面左上角OE为坐标原点建立坐标系OE-XEYE，摄像机视场范围内任意一点(xw,yw,zw)对应图像坐标系中坐标(xE,yE)。

图1 激光摄像式传感器成像及标定示意Fig. 1 Imaging and calibration diagram of laser camera sensor

设R和T为摄像机坐标系转化为世界坐标系的旋转矩阵和平移矩阵，即摄像机外部参数，如式（1）。

假设α,β,μ,ν,γ为摄像机内部参数，其中α和β分别是u轴和v轴的尺度因子（或称为有效焦距），（μ,ν）是光学中心，γ是u轴和v轴的不垂直因子。由于镜头畸变的存在，本文将镜头径向畸变系数(k1和k2)、薄棱畸变系数(p1和p2)及偏心畸变系数(s1和s2)考虑进去，建立非线性标定模型。由摄影投射定理可知，OCXCYCZC与OE-XEYE坐标系变换关系为

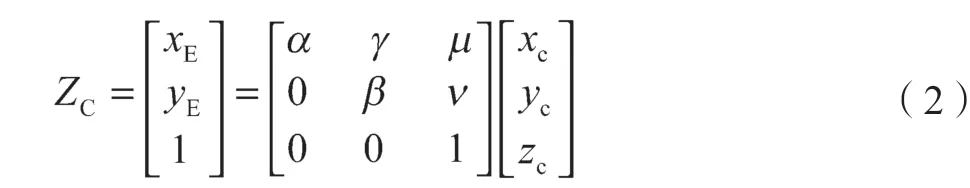
由于OW-XWYW平面与激光平面共面，标定过程中参考点均在激光平面上，故可令zw=0。根据式（1）和式（2），可推出激光摄像式传感器图像坐标系与世界坐标系的关系：

式中：a1～a9为激光摄像式传感器的摄像机线性模型参数。

激光平面上任意点P的图像像素坐标为(xE,yE)。考虑镜头畸变后，实际成像像素坐标为(xD,yD)，则畸变前后关系如下：

式中：δx与δy分别为XE方向和YE方向的畸变因子。

图像中心O点像素坐标为(x0,y0)，其与考虑畸变后的P点在图像坐标系O-uv下的坐标(u,v)关系如下：

畸变因子δx与δy的表达式如式（6）所示，其中系数k1,k2,p1,p2,s1,s2被统称为镜头畸变参数。

将式（4）和式（6）代入式（3），得到激光摄像式传感器的非线性标定模型，如式（7）所示，其传感器标定参数（a1～a8,k1,k2,p1,p2,s1及s2）的目标函数如式（8）所示。

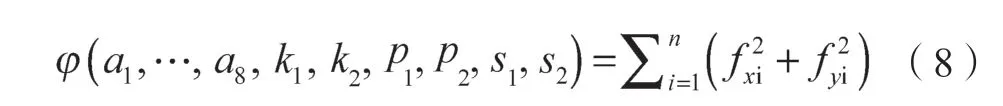
式中：n——标定特征点数量。

2 标定模型参数求解方法

视觉标定过程中常用的参数求解方法主要有非线性最小二乘法、高斯-牛顿迭代算法以及L-M 算法。在非线性最小二乘法及高斯-牛顿迭代算法的求解过程中，会出现矩阵奇异或接近奇异的情形，使方程求解过程变得十分困难；而L-M 算法通过改变矩阵的特征值结构来解决该问题，同时L-M 算法在求解过程中可以通过参数设置灵活调节收敛速度。

2.1 非线性最小二乘法[20]

由于式（8）是非线性方程组，无法直接通过线性最小二乘法求解，故通过非线性最小二乘法求解激光摄像式传感器标定参数，求解步骤如下：

（1）将传感器标定参数分成两部分，即线性模型参数(a1,a2, …,a8)和畸变参数(k1,k2,p1,p2,s1,s2)。

（2）将畸变参数作为已知量代入式（8）并将非线性方程组转化为线性方程组，采用线性最小二乘法求解线性模型参数。

（3）将步骤（2）中计算得到的线性模型参数作为已知量代入式（8），将式（8）转化为关于畸变参数的线性方程组并采用线性最小二乘法求解畸变参数。

（4）重复步骤（2）和步骤（3），通过多次迭代，最终接近最优解。

2.2 高斯-牛顿迭代法

高斯-牛顿迭代法是一种非线性优化算法，用来求解激光摄像式传感器的标定参数，具体步骤如下：

（1）采用2.1 节中非线性最小二乘法迭代5 次，将求解得到的激光摄像式传感器的标定参数作为高斯-牛顿迭代的初值并根据式（8）建立高斯-牛顿优化计算模型[21]：

利用式（10）可求得Guass-Newton 方向参数Di，其中F=[fx1,fy1, …,fxi,fyi]T。

（2）沿着Guass-Newton 方向Di作一维搜索，求得步长m使式（11）成立。

2.3 基于极大似然估计的L-M 算法

在高斯-牛顿迭代计算过程中，求解矩阵(ATA)-1时，容易出现矩阵ATA奇异或接近奇异的情形，这时求解式（10）得到的Guass-Newton 方向Di误差较大，极易导致最终迭代计算结果无法收敛。

针对高斯-牛顿迭代法中矩阵ATA奇异或接近奇异的情形，L-M 算法通过增加正定对角矩阵的方式改变矩阵ATA的特征值结构，使其变成条件数较好的对称正定矩阵，弥补了高斯-牛顿迭代法的不足。

L-M 算法以高斯-牛顿迭代法为基础，令

式中：I为i阶单位矩阵；α为正实数。

当α=0 时，Di即为Guass-Newton 方向；当α足够大时，逆矩阵(ATA+αI)-1主要取决于αI，Di接近最速下降方向。一般而言，α初值为0.001，变换因子β=10，允许误差ε=0.000 01。当F(X i+1)>F(X i)且|ATA|≤ε时，停止计算；否则，置α=αβ，继续迭代。当F(X i+1)＜F(X i)且|ATA|≤ε时，停止计算；否则，置α=α/β，继续迭代。

本算法提出先采用极大似然估计法求得由高斯噪声和散粒噪声引起的图像坐标误差，进而在标定模型参数求解过程中剔除高斯噪声和散粒噪声的干扰，将实际成像像素坐标减去由高斯噪声和散粒噪声引起的像素坐标误差，然后用L-M 法求出参数(a1, …,a8,k1, …,s2)的最优解。

设激光平面上任意点P的图像像素坐标为(xE,yE)，考虑镜头畸变后，实际成像像素坐标为(xD,yD)。实际上，图像坐标的提取过程会受到高斯噪声、散粒噪声的干扰[22-23]。一般而言，高斯噪声引起的像素坐标误差服从正态分布，而散粒噪声引起的像素坐标误差服从伽马分布，误差(εx,εy)如式（14）所示。

任意点P对应的由高斯噪声引起的像素坐标误差概率密度函数f(p1)如式（15）所示。

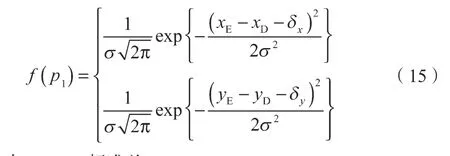
式中：σ——标准差。

任意点P对应的由散粒噪声引起的像素坐标误差概率密度函数f(p2)如下：

构造极大似然函数L(p1)和L(p2)，其等于所有点(p1,p2, …,pb)对应的像素坐标误差概率密度函数乘积，具体如式（17）和式（18）所示。

根据极大似然原理[23-25]，当L(p1)和L(p2)取最大值时，所得的估计值即为像素坐标误差值；根据式（17）和式（18）可知，当L(p1)和L(p2)取最大值时，式（19）取值最小。

由激光摄像式传感器模型可知，式（19）（目标函数）为非线性函数，采用L-M 算法对该目标函数进行求解，容易得到目标函数的极大似然估计值，也就可以得到像素坐标误差值。

3 激光摄像式传感器标定试验

3.1 标定试验

针形靶标标定原理如图2 所示，采用针形靶标对标定平台、刻度尺、滑动丝杆、计算机进行标定，再通过数据采集软件和Matlab 实现对标定数据的采集和处理。

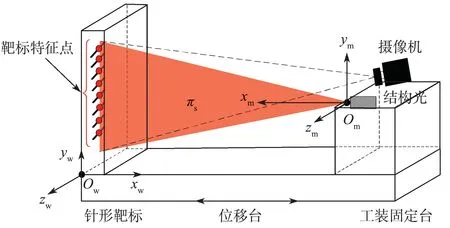
图2 针形靶标标定平台示意图Fig. 2 Schematic diagram of the calibration platform for needle target diagram

激光摄像式传感器针形靶标标定步骤如下：

步骤一，安装激光摄像式传感器。调整传感器在工装固定台的位置，确保结构光始终垂直投射于针形靶标上，再将激光摄像式传感器固定在平台上。

步骤二，摄像机捕捉结构光平面投射于针形靶标形成的光斑图像，并提取光斑中心作为特征点的图像坐标，同时记录光斑在世界坐标系下的世界坐标。

步骤三，以相同间距移动针形靶标，每次移动后重复步骤二，尽量使所得特征点覆盖摄像机全部视场范围。

步骤四，根据上述的标定模型参数求解方法，将获取的特征点对代入计算模型，获得最优解。

结构光平面投射在针形靶标上形成的光斑图像如图3 所示，图中仅列出了针形靶标在位移平台5 个不同位置的光斑图像。选取光斑图像的中心作为标定点对的特征点图像坐标，特征点世界坐标则为结构光与针形靶针相交位置距离固定平台的水平距离和垂直距离。等间隔地移动靶标，共获取800 个标定特征点对，特征点的图像坐标如图4（a）所示，世界坐标如图4（b）所示。

图3 针形靶标光斑图像Fig. 3 Spot images of needle target

图4 特征点坐标标定Fig. 4 Coordinate calibration of feature points

针对实验获得的800 组标定数据，采用非线性最小二乘法迭代5 次，发现传感器标定模型参数(a1, …,a8,k1,k2,p1,p2,s1,s2)的值比较稳定，迭代5 次得到的传感器标定模型参数值如表1、表2 所示。

表1 标定线性模型参数Tab. 1 Calibration linear model parameters

表2 标定镜头畸变参数Tab. 2 Calibration lens distortion parameters

将传感器标定模型参数作为基于极大似然估计的L-M 优化算法的初值，通过L-M 算法寻找传感器标定模型参数最优值，标定线性模型参数收敛曲线如图5 所示，标定镜头畸变参数收敛曲线如图6 所示。

图5 标定线性模型参数收敛曲线Fig. 5 Convergence curves of calibration linear model parameters

图6 标定镜头畸变参数收敛曲线Fig. 6 Convergence curves of calibration lens distortion parameters

迭代10 步之后，参数基本收敛，此时所得到的标定参数为最优解，如表3 和表4 所示。

表3 标定镜头畸变参数Tab. 3 Calibration lens distortion parameters

表4 标定线性模型参数Tab. 4 Calibration linear model parameters

3.2 标定试验结果误差分析

针对标定试验中得到的标定数据，分别采用非线性最小二乘法、高斯-牛顿迭代法和基于极大似然估计的L-M 优化法这3 种方法进行处理，得到模型参数(a1, …,a8,k1, …,s2)的最优值，然后将参数代回标定模型中，进行逆向运算。将800 组特征点的像素坐标分别代入标定模型，分别求得特征点在世界坐标系下的坐标值(xw1,yw1), (xw2,yw2), (xw3,yw3)。以原始世界坐标(xw,yw)为标准，(Δx, Δy)为世界坐标系下的误差，采用非线性最小二乘法得到的误差为(Δx1, Δy1)=(xw-xw1,yw-yw1)，分别如图7（a）和图7（b）所示；采用高斯-牛顿迭代法得到的误差为(Δx2, Δy2)=(xw-xw2,yw-yw2)，分别如图7（c）和图7（d）所示；采用基于极大似然估计的L-M 优化法得到的误差为(Δx3, Δy3)=(xw-xw3,yw-yw3)，分别如图7（e）和图7（f）所示。

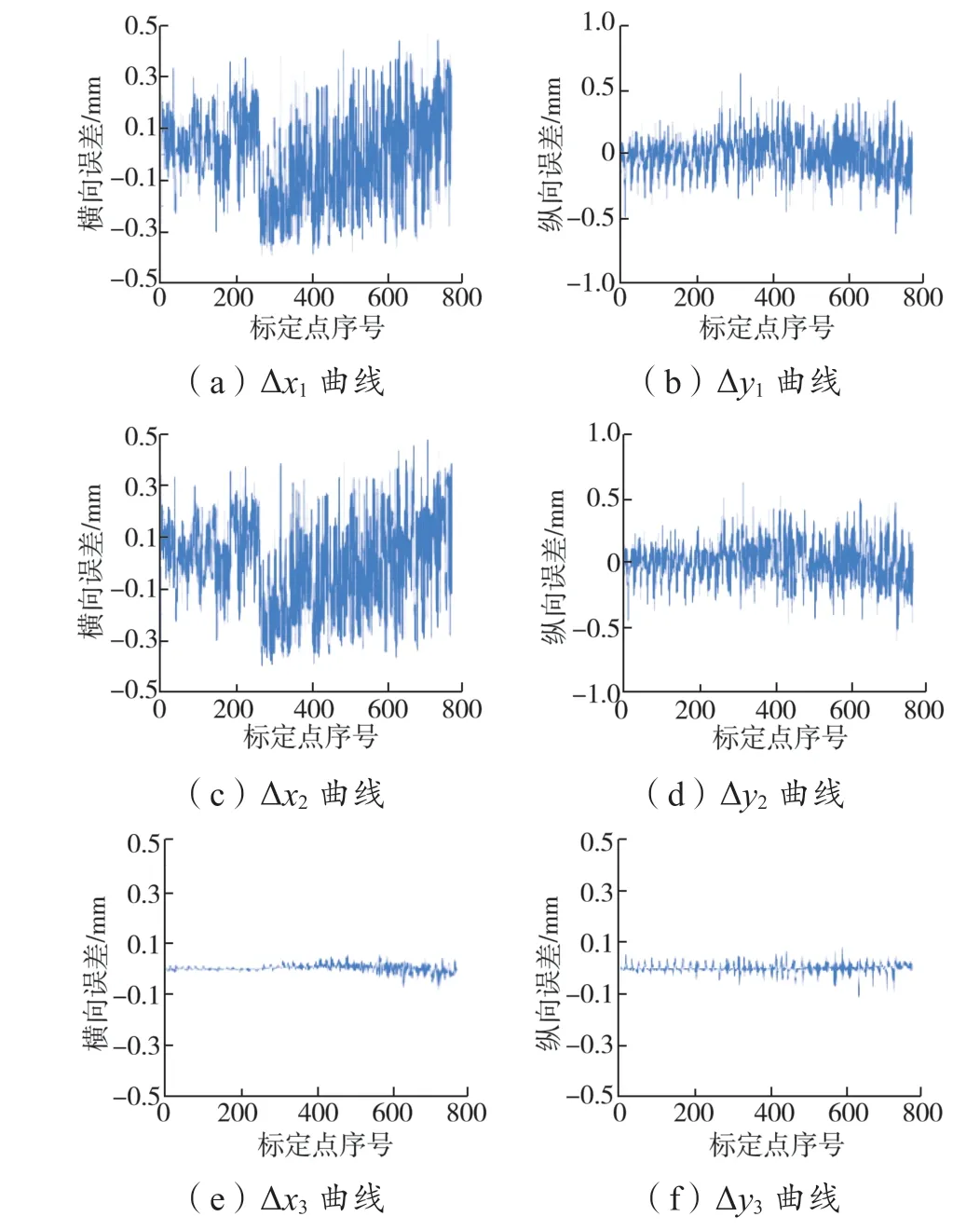
图7 800 组特征点世界坐标系下的误差曲线Fig. 7 Error curves of 800 groups of characteristic points in world coordinate system

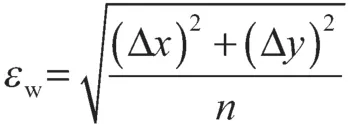
表5 800 组特征点坐标算法误差 Tab. 5 Errors of 800 groups of feature points（单位：mm）

为确保实验的可靠性和算法的有效性，另获取1 000 组未参与标定模型计算的数据进行误差分析（图8），采用3 种方法分别计算得到该组数据的世界坐标为(xw4,yw4)，(xw5,yw5)和(xw6,yw6)。

图8 1 000 组未参与标定模型计算的数据误差分析Fig. 8 Error analysis of 1 000 groups of data not involved in calibration model calculation

非线性最小二乘法得到的误差为(Δx4, Δy4)，如图8（a）和图8（b）所示；高斯-牛顿迭代法得到的误差为(Δx5, Δy5)，分别如图8（c）和图8（d）所示；基于极大似然估计的L-M 优化法得到的误差(Δx6, Δy6)，分别如图8（e）和图8（f）所示。采用这3 种方法得到的误差最大值分别为εmax4，εmax5，εmax6；误差平均值分别为εave4，εave5，εave6；重投影误差方均根值分别εw4，εw5，εw6，具体如表6 所示。

表6 1 000 组特征点坐标算法误差 Tab. 6 Errors of 1 000 groups of feature points（单位：mm）

综合表5 和表6，对两组数据进行平均计算，得到非线性最小二乘法、高斯-牛顿法、基于极大似然估计的L-M 算法误差最大值分别是（0.493, 0.584），（0.436, 0.586），（0.081, 0.112）；误差平均值分别是（0.156, 0.121），（0.147, 0.120），（0.011, 0.012）；重投影误差方均根值分别是0.245 7, 0.236 6, 0.024 3。可见，基于极大似然估计L-M 算法的标定精度误差最大值较非线性最小二乘法的和高斯-牛顿法的分别减小了（0.412 mm, 0.472 mm）和（0.355 mm, 0.474 mm）； 误差平均值分别减小了（0.145 mm, 0.109 mm）和（0.136 mm, 0.108 mm）；重投影误差方均根值分别减小了0.221 4 mm 和0.212 3 mm。

4 结语

本文建立了基于非线性最小二乘法、高斯-牛顿迭代法及基于极大似然估计的L-M 优化算法的激光摄像式传感器标定模型；并采用3 种不同方法进行了标定模型参数求解。其中非线性最小二乘法迭代300 次后模型参数基本收敛，高斯-牛顿迭代法迭代20 次后模型参数基本收敛，基于极大似然估计的L-M 算法迭代10 次后模型参数基本收敛。对于基于极大似然估计的L-M算法，因考虑高斯噪声与散粒噪声影响，对已有标定算法进行了优化，使得标定精度有效提升；但该算法的计算复杂度相对较高，后续研究中需继续优化。